一类3-缠绕的Jones多项式

The Jones Polynomials of a Class of 3-Tangles

摘要: 选定了3-缠绕的一种定向方式，结合Giller的房间理论给出任意两个3-缠绕的复合的Jones多项式。接着，通过研究计算得到了一类特殊3-缠绕的Jones多项式的递推公式以及由其闭包所形成的链环的Jones多项式。

Abstract: An unusual orientation of 3-tangles is given, and the Jones polynomial of the concatenation of two 3-tangles is given by Giller’s room theory. Then, the recursion formula of the Jones polynomials of a special kind of 3-tangles is obtained by studying and calculating. In addition, the formula to obtain the Jones polynomial of the links obtained from their closure is given.

1. 引言

纽结理论研究纽结和链环在连续形变下保持不变的特性，是拓扑学中引人入胜的一支。等价分类问题是纽结理论的中心，人们通过寻找纽结不变量来解决纽结的等价问题。纽结多项式 [1] [2] [3] [4] 是常见的纽结不变量之一，而Jones多项式是重要的纽结多项式，它为研究纽结与链环的手征性提供了有力的工具。

近几年，不同定向的3-缠绕的多项式成为了数学界的一个关注点且有了大量的研究成果 [5] - [10]。在文献 [6] 中，Cabrera给出了3-缠绕的一种定向方式，在此基础上研究了5种不同的方法闭合3-缠绕得到纽结或链环，给出了公式计算两个3-缠绕的复合的闭包的Conway多项式。文献 [9] 给出了3-缠绕的一种常规定向，也即3-辫子，并在此基础上研究了3-辫子的复合的六种不同闭包方法得到的链环的Conway多项式。文献 [10] 给出了3-缠绕不同于文献 [9] 的新的定向，并利用Giller的房间理论计算了它们的Conway多项式和Alexander多项式。

本文在前人的研究基础上，利用Giller的房间理论进一步研究了一类特殊3-缠绕 ${\epsilon }^{2k}$ 的Jones多项式。在预备知识我们将介绍一些有关3-缠绕和纽结Jones多项式的一些基本概念；在第二部分，我们将通过Giller的房间理论给出任意两个3-缠绕的复合的Jones多项式；第三部分，通过研究计算得到一类特殊的3-缠绕 ${\epsilon }^{2k}$ 的Jones多项式的递推公式，并进一步计算由其闭包所形成的链环的Jones多项式。

2. 预备知识

2.1. 3-缠绕的基本概念

定义2.1 [10] n-缠绕指一个偶对 $\left(B^3,T\right)$，其中 $B^3$ 是一个三维实心球， $T\subset B^{\text{3}}$ 是一个具有非空边界的一维嵌入子流形，它包含n个弧(即n个同胚于 $\left[0,1\right]$ 的子集)，并满足 $\partial T=T\cap \partial B^3$。

本文只讨论3-缠绕，且记为T而不是 $\left(B^3,T\right)$。

定义2.2 [11] n-辫子是由n条线组成的集合，这些线都连接在顶部和底部的水平线上(如图1)，沿着任意一根线从顶部移动到底部时方向总是向下的，即每根线与两根水平线之间的任何水平面相交且只相交一次。n-辫子是n-缠绕的一种特殊情况。

Figure 1. A braid

图1. 辫子

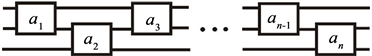(a) (b)

Figure 2. 3-braid ${\rm T}\left(a_1,a_2,\cdots ,a_n\right)$ with (a) n odd and (b) n even

图2. 3-辫子 ${\rm T}\left(a_1,a_2,\cdots ,a_n\right)$ 其中(a) n为奇数(b) n为偶数

本文研究的是3-辫子，并使用符号 ${\rm T}\left(a_1,a_2,\cdots ,a_n\right)$ [10] 表示，其中 $a_i,n$ 均为整数， $i=1,2,\cdots ,n$。如图2所示， $a_i$ 表示交叉点的类型和数量，规定：若 $a_i=0$，则3-辫子无交叉点，否则

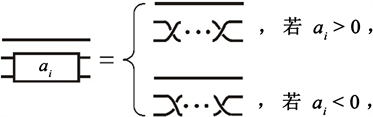
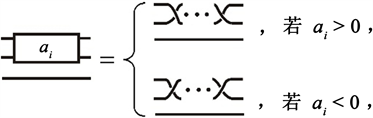
定义2.3 [10] 如图3所示3-辫子 ${\rm T}\left(1,-1,1\right)$ 是一个半扭转，记为 $\epsilon$。

Figure 3. 3-braid ${\rm T}\left(1,-1,1\right)$

图3. 3-辫子 ${\rm T}\left(1,-1,1\right)$

定义2.4 [12] 房间R是R²中的一个连通域，它具有相同数量的有向的进出绳。本文讨论的是如图4所示的3-房间。

Figure 4. The 3-room R

图4. 3-房间R

定义2.5 [12] 所有连通房间进出绳的集合，用 $S\left(R\right)$ 表示。 $S\left(R\right)$ 的一个元素称为R的居住者。(图5)

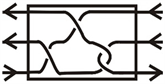
Figure 5. An inhabitant of the 3-room R

图5. 3-房间R的一个居住者

事实上，带有由进出绳诱导的方向的R的居住者即为一个有向3-缠绕。

定义2.6 [12] 在 $S\left(R\right)$ 中通过连接的方式定义一个记为“ $\cdot$ ”的运算(如图6)，将构造一些链环。

Figure 6. Inhabitants S and T in $S\left(R\right)$ and their concatenation $S\cdot T$

图6. $S\left(R\right)$ 中的居住者S和T以及它们的复合 $S\cdot T$

2.2. 纽结的Jones多项式

有向链环定义的一个多项式不变量是Jones多项式 $V\left(L\right)$。这个多项式可以通过以下拆接关系 [11] 来计算：

1) $t^{-1}V\left(L_{+}\right)-tV\left(L_{-}\right)=\left(t^{\frac{1}{2}}-t^{-\frac{1}{2}}\right)V\left(L_0\right)$，

2) V() = 1，

其中是平凡纽结， $L_{+},L_{-},L_0$ 是三个只在一个交叉点处不同的链环。(图7)

Figure 7. Skein triple

图7. 拆接关系

引理2.1 [13] 若L是具有c个分支的平凡链环，则 $V\left(L\right)={\delta }^{c-1}$，其中 $\delta =-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)$。

引理2.2 [14] 设L为任意有向链环，则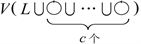 = ${\delta }^{c}V\left(L\right)$，其中 $\delta =-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)$。

3. 3-缠绕的Jones多项式

在 $S\left(R\right)$ 中有6种不同的方式连接R的进绳和出绳。图8是连接R的进出绳后具有最少交叉点数的居住者，用 ${\chi }_i$ 表示，其中 $i=1,2,\cdots ,6$。这样的居住者的集合 $\left\{{\chi }_i,i=1,2,\cdots ,6\right\}$ 称为 $S\left(R\right)$ 的基居住者集 [10]。

Figure 8. Basic inhabitants of $S(\; R\; )$

图8. $S\left(R\right)$ 的基居住者

设F是 $Z\left[\sqrt{t}\right]$ 的分式域， $V\left(R\right)$ 表示 $S\left(R\right)$ 在F上生成的自由向量空间， $N\left(R\right)$ 是 $t^{-1}{T}_{+}-t{T}_{-}-\left(t^{\frac{1}{2}}-t^{-\frac{1}{2}}\right)T_0$ 在F上生成的子空间，其中 $\left(T_{+},T_{-},T_0\right)$ 是一个拆接关系。记 $L\left(R\right)$ 是商向量空间 $\frac{V\left(R\right)}{N\left(R\right)}$。特别地，图8所示的基居住者是 $L\left(R\right)$ 的基。因此， $L\left(R\right)$ 中的每个元素都可以唯一地表示成基居住者的线性组合。

对任意的 $T\in S\left(R\right)$，通过对图T反复应用Jones多项式的拆接关系，直到只剩下基居住者为止，就得到了T的Jones多项式。因此

$V\left(T\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_{i}V\left({\chi }_i\right)}$，其中 $p_i\in Z\left[\sqrt{t}\right]$。

定理3.1设 $T_1,T_2$ 是两个3-缠绕，且

$V\left(T_1\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_{i}V\left({\chi }_i\right)}$， $V\left(T_2\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{q}_{i}V\left({\chi }_i\right)}$，

那么

$\begin{array}{c}V\left(T_1\cdot T_2\right)=\left[p_1{q}_1+p_3{q}_3{t}^2\right]V\left({\chi }_1\right)+[p_1{q}_2+p_2{q}_1-p_2{q}_2\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+p_2{q}_4+p_3{q}_4{t}^2+p_5{q}_2\\ +p_5{q}_3{t}^2-p_5{q}_4\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_2\right)+\left[p_1{q}_3+p_3{q}_1+p_3{q}_3\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\right]V\left({\chi }_3\right)\\ +[p_1{q}_4+p_3{q}_2+p_3{q}_4\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)+p_4{q}_1-p_4{q}_2\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+p_4{q}_4+p_6{q}_2+p_6{q}_3{t}^2\\ -p_6{q}_4\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_4\right)+[p_1{q}_5+p_2{q}_3-p_2{q}_5\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+p_2{q}_6+p_3{q}_6{t}^2+p_5{q}_1\\ +p_5{q}_3\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)+p_5{q}_5-p_5{q}_6\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_5\right)+[p_1{q}_6+p_3{q}_5+p_3{q}_6\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\\ +p_4{q}_3-p_4{q}_5\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+p_4{q}_6+p_6{q}_1+p_6{q}_3\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)+p_6{q}_5-p_6{q}_6\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V(\; \chi \; 6\; )\end{array}$

证明：对 $T_1,T_2$ 中的 $T_1$ 应用Jones多项式的拆接公式，我们有

$V\left(T_1\cdot T_2\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_{i}V\left({\chi }_i\cdot T_2\right)}={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_i\left({\displaystyle \underset{j=1}{\overset{6}{\sum }}{q}_j}V\left({\chi }_i\cdot {\chi }_j\right)\right)}$

计算 $V\left({\chi }_i\cdot {\chi }_j\right)$，并将多项式化简后即可得结果。下面我们计算 ${\chi }_2\cdot {\chi }_j$ 的情况，其他情况可类似计算。(表1)

Table1. $V\left({\chi }_2\cdot {\chi }_j\right)$

表1. $V\left({\chi }_2\cdot {\chi }_j\right)$

4. 3-缠绕 ${\epsilon }^{2k}$ 以及链环 $C\left({\epsilon }^{2k}\right)$ 的Jones多项式

4.1. 3-缠绕 ${\epsilon }^{2k}$ 的Jones多项式

定理4.1记 $A=t^{\frac{1}{2}}-t^{-\frac{1}{2}}$，则对任意的 $k\in N$，有 $V\left({\epsilon }^{2k}\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{\alpha }_{i_k}}V\left({\chi }_i\right)$，其中

$\begin{array}{l}{\alpha }_{1_0}=1,{\alpha }_{2_0}={\alpha }_{3_0}={\alpha }_{4_0}={\alpha }_{5_0}={\alpha }_{6_0}=0,\\ {\alpha }_{1_k}=t^{-2}{\alpha }_{1_{k-1}}+A{t}^{-1}{\alpha }_{3_{k-1}},{\alpha }_{2_k}=-A{t}^{-1}{\alpha }_{1_{k-1}}+{\alpha }_{2_{k-1}},{\alpha }_{3_k}=A{t}^{-3}{\alpha }_{1_{k-1}}+\left(t^{-2}+A^2{t}^{-2}\right){\alpha }_{3_{k-1}},\\ {\alpha }_{4_k}=-A{t}^{-1}{\alpha }_{3_{k-1}}+{\alpha }_{4_{k-1}},{\alpha }_{5_k}=-A{t}^{-1}{\alpha }_{3_{k-1}}+\left(2t^{-2}+A^2{t}^{-2}+1-t^{-3}-t^{-1}\right){\alpha }_{5_{k-1}},\\ {\alpha }_{6_k}=-A{t}^{-3}{\alpha }_{1_{k-1}}-A^2{t}^{-2}{\alpha }_{3_{k-1}}+\left(2t^{-2}+A^2{t}^{-2}+1-t^{-3}-t^{-1}\right){\alpha }_{6_{k-1}}\end{array}$

证明：通过对k作归纳法证明该定理。 $k=0$ 时， ${\epsilon }^{2k}={\chi }_1$，则有 $V\left({\epsilon }^{2k}\right)=V\left({\chi }_1\right)$。此时 ${\alpha }_{1_0}=1$， ${\alpha }_{2_0}={\alpha }_{3_0}={\alpha }_{4_0}={\alpha }_{5_0}={\alpha }_{6_0}=0$。 $k=1$ 时，经过计算可以得到

$V\left({\epsilon }^{2k}\right)=V\left({\epsilon }^2\right)=t^{-2}V\left({\chi }_1\right)-\left(t^{\frac{1}{2}}-t^{-\frac{1}{2}}\right)t^{-1}V\left({\chi }_2\right)+\left(t^{\frac{1}{2}}-t^{-\frac{1}{2}}\right)t^{-3}V\left({\chi }_3\right)-\left(t^{\frac{1}{2}}-t^{-\frac{1}{2}}\right)t^{-3}V(\; \chi \; 6\; )$

此时 ${\alpha }_{1_1}=t^{-2}$， ${\alpha }_{2_1}=-A{t}^{-1}$， ${\alpha }_{3_1}=A{t}^{-3}$， ${\alpha }_{4_1}={\alpha }_{5_1}=0$， ${\alpha }_{6_1}=-A{t}^{-3}$。

现在假设 $k-1$ 时定理4.1成立。对于k时，应用定理3.1，我们有

$\begin{array}{c}V\left({\epsilon }^{2k}\right)=V\left({\epsilon }^{2\left(k-1\right)}\cdot {\epsilon }^2\right)\\ =\left[{\alpha }_{1_{k-1}}{\alpha }_{1_1}+{\alpha }_{3_{k-1}}{\alpha }_{3_1}{t}^2\right]V\left({\chi }_1\right)+[{\alpha }_{1_{k-1}}{\alpha }_{2_1}+{\alpha }_{2_{k-1}}{\alpha }_{1_1}-{\alpha }_{2_{k-1}}{\alpha }_{2_1}\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+{\alpha }_{2_{k-1}}{\alpha }_{4_1}\\ +{\alpha }_{3_{k-1}}{\alpha }_{4_1}{t}^2+{\alpha }_{5_{k-1}}{\alpha }_{2_1}+{\alpha }_{5_{k-1}}{\alpha }_{3_1}{t}^2-{\alpha }_{5_{k-1}}{\alpha }_{4_1}\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_2\right)\\ +\left[{\alpha }_{1_{k-1}}{\alpha }_{3_1}+{\alpha }_{3_{k-1}}{\alpha }_{1_1}+{\alpha }_{3_{k-1}}{\alpha }_{3_1}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\right]V\left({\chi }_3\right)+[{\alpha }_{1_{k-1}}{\alpha }_{4_1}+{\alpha }_{3_{k-1}}{\alpha }_{2_1}+{\alpha }_{3_{k-1}}{\alpha }_{4_1}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\\ +{\alpha }_{4_{k-1}}{\alpha }_{1_1}-{\alpha }_{4_{k-1}}{\alpha }_{2_1}\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+{\alpha }_{4_{k-1}}{\alpha }_{4_1}+{\alpha }_{6_{k-1}}{\alpha }_{2_1}+{\alpha }_{6_{k-1}}{\alpha }_{3_1}{t}^2-{\alpha }_{6_{k-1}}{\alpha }_{4_1}\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V(\; \chi \; 4\; )\end{array}$

$\begin{array}{c}+[{\alpha }_{1_{k-1}}{\alpha }_{5_1}+{\alpha }_{2_{k-1}}{\alpha }_{3_1}-{\alpha }_{2_{k-1}}{\alpha }_{5_1}\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+{\alpha }_{2_{k-1}}{\alpha }_{6_1}+{\alpha }_{3_{k-1}}{\alpha }_{6_1}{t}^2+{\alpha }_{5_{k-1}}{\alpha }_{1_1}+{\alpha }_{5_{k-1}}{\alpha }_{3_1}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\\ +{\alpha }_{5_{k-1}}{\alpha }_{5_1}-{\alpha }_{5_{k-1}}{\alpha }_{6_1}\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_5\right)+[{\alpha }_{1_{k-1}}{\alpha }_{6_1}+{\alpha }_{3_{k-1}}{\alpha }_{5_1}+{\alpha }_{3_{k-1}}{\alpha }_{6_1}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)+{\alpha }_{4_{k-1}}{\alpha }_{3_1}\\ -{\alpha }_{4_{k-1}}{\alpha }_{5_1}\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+{\alpha }_{4_{k-1}}{\alpha }_{6_1}+{\alpha }_{6_{k-1}}{\alpha }_{1_1}+{\alpha }_{6_{k-1}}{\alpha }_{3_1}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)+{\alpha }_{6_{k-1}}{\alpha }_{5_1}-{\alpha }_{6_{k-1}}{\alpha }_{6_1}\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V(\; \chi \; 6\; )\end{array}$

将 ${\alpha }_{i_1}\left(i=1,2,\cdots ,6\right)$ 的值代入后，有

$\begin{array}{c}V\left({\epsilon }^{2k}\right)=\left[{\alpha }_{1_{k-1}}{t}^{-2}+{\alpha }_{3_{k-1}}A{t}^{-3}{t}^2\right]V\left({\chi }_1\right)+[{\alpha }_{1_{k-1}}\left(-A{t}^{-1}\right)+{\alpha }_{2_{k-1}}{t}^{-2}-{\alpha }_{2_{k-1}}\left(-A{t}^{-1}\right)\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+{\alpha }_{5_{k-1}}\left(-A{t}^{-1}\right)\\ \begin{array}{c}\\ \end{array}+{\alpha }_{5_{k-1}}A{t}^{-3}{t}^2]V\left({\chi }_2\right)+\left[{\alpha }_{1_{k-1}}A{t}^{-3}+{\alpha }_{3_{k-1}}{t}^{-2}+{\alpha }_{3_{k-1}}A{t}^{-3}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\right]V\left({\chi }_3\right)+[{\alpha }_{3_{k-1}}\left(-A{t}^{-1}\right)+{\alpha }_{4_{k-1}}{t}^{-2}\begin{array}{c}\\ \end{array}\\ -{\alpha }_{4_{k-1}}\left(-A{t}^{-1}\right)\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)+{\alpha }_{6_{k-1}}\left(-A{t}^{-1}\right)+{\alpha }_{6_{k-1}}A{t}^{-3}{t}^2]V\left({\chi }_4\right)+[{\alpha }_{2_{k-1}}A{t}^{-3}+{\alpha }_{2_{k-1}}\left(-A{t}^{-3}\right)\begin{array}{c}\\ \end{array}\\ +{\alpha }_{3_{k-1}}\left(-A{t}^{-3}\right)t^2+{\alpha }_{5_{k-1}}{t}^{-2}+{\alpha }_{5_{k-1}}A{t}^{-3}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)-{\alpha }_{5_{k-1}}\left(-A{t}^{-3}\right)\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_5\right)+[{\alpha }_{1_{k-1}}\left(-A{t}^{-3}\right)\begin{array}{c}\\ \end{array}\\ +{\alpha }_{3_{k-1}}\left(-A{t}^{-3}\right)\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)+{\alpha }_{4_{k-1}}A{t}^{-3}+{\alpha }_{4_{k-1}}\left(-A{t}^{-3}\right)+{\alpha }_{6_{k-1}}{t}^{-2}+{\alpha }_{6_{k-1}}A{t}^{-3}\left(t^{\frac{3}{2}}-t^{\frac{1}{2}}\right)\end{array}$

$\begin{array}{c}-{\alpha }_{6_{k-1}}\left(-A{t}^{-3}\right)\left(t^{\frac{1}{2}}+t^{\frac{5}{2}}\right)]V\left({\chi }_6\right)\\ =\left[t^{-2}{\alpha }_{1_{k-1}}+A{t}^{-1}{\alpha }_{3_{k-1}}\right]V\left({\chi }_1\right)+\left[-A{t}^{-1}{\alpha }_{1_{k-1}}+{\alpha }_{2_{k-1}}\right]V\left({\chi }_2\right)+\left[A{t}^{-3}{\alpha }_{1_{k-1}}+\left(t^{-2}+A^2{t}^{-2}\right){\alpha }_{3_{k-1}}\right]V\left({\chi }_3\right)\\ +\left[-A{t}^{-1}{\alpha }_{3_{k-1}}+{\alpha }_{4_{k-1}}\right]V\left({\chi }_4\right)+\left[-A{t}^{-1}{\alpha }_{3_{k-1}}+\left(2t^{-2}+A^2{t}^{-2}+1-t^{-3}-t^{-1}\right){\alpha }_{5_{k-1}}\right]V\left({\chi }_5\right)\\ +\left[-A{t}^{-3}{\alpha }_{1_{k-1}}-A^2{t}^{-2}{\alpha }_{3_{k-1}}+\left(2t^{-2}+A^2{t}^{-2}+1-t^{-3}-t^{-1}\right){\alpha }_{6_{k-1}}\right]V(\; \chi \; 6\; )\end{array}$

此时

$\begin{array}{l}{\alpha }_{1_k}=t^{-2}{\alpha }_{1_{k-1}}+A{t}^{-1}{\alpha }_{3_{k-1}},{\alpha }_{2_k}=-A{t}^{-1}{\alpha }_{1_{k-1}}+{\alpha }_{2_{k-1}},{\alpha }_{3_k}=A{t}^{-3}{\alpha }_{1_{k-1}}+\left(t^{-2}+A^2{t}^{-2}\right){\alpha }_{3_{k-1}},\\ {\alpha }_{4_k}=-A{t}^{-1}{\alpha }_{3_{k-1}}+{\alpha }_{4_{k-1}},{\alpha }_{5_k}=-A{t}^{-1}{\alpha }_{3_{k-1}}+\left(2t^{-2}+A^2{t}^{-2}+1-t^{-3}-t^{-1}\right){\alpha }_{5_{k-1}},\\ {\alpha }_{6_k}=-A{t}^{-3}{\alpha }_{1_{k-1}}-A^2{t}^{-2}{\alpha }_{3_{k-1}}+\left(2t^{-2}+A^2{t}^{-2}+1-t^{-3}-t^{-1}\right){\alpha }_{6_{k-1}}\end{array}$

定理4.1得证。

4.2. 链环 $C\left({\epsilon }^{2k}\right)$ 的Jones多项式

利用3-缠绕可以构造一些链环。设T是一个3-缠绕，如图9所示方式闭合3-缠绕可以得到纽结或链环。记为 $C\left(T\right)$。

定理4.2设T是一个3-缠绕且 $V\left(T\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_{i}V\left({\chi }_i\right)}$，那么

$V\left(C\left(T\right)\right)={\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)}^2{p}_1-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)p_2-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)p_3+p_4+p_5-\left(t^{\frac{5}{2}}+t^{\frac{1}{2}}\right)p_6$。

Figure 9. Link $C(\; T\; )$

图9. 链环 $C(\; T\; )$

证明：由 $V\left(T\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_{i}V\left({\chi }_i\right)}$，有 $V\left(C\left(T\right)\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{p}_{i}V\left(C\left({\chi }_i\right)\right)}$。如图10，我们可以看到， $i=1$ 时， $C\left({\chi }_i\right)$ 是分支数为3的平凡链环； $i=2,3$ 时， $C\left({\chi }_i\right)$ 是分支数为2的平凡链环； $i=4,5$ 时， $C\left({\chi }_i\right)$ 为平凡结。由引理2.1有 $V\left(C\left({\chi }_1\right)\right)={\delta }^2={\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)}^2$， $V\left(C\left({\chi }_2\right)\right)=V\left(C\left({\chi }_3\right)\right)=\delta =-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)$， $V\left(C\left({\chi }_4\right)\right)=V\left(C\left({\chi }_5\right)\right)=1$。此外，对 $C\left({\chi }_6\right)$ 应用拆接关系有

$t^{-1}V$ () $-tV$ () $=(t^{\frac{1}{2}}-t^{-\frac{1}{2}})V$ ()，

得到 $V\left(C\left({\chi }_6\right)\right)=-t^{\frac{5}{2}}-t^{\frac{1}{2}}$。因此，

$V\left(C\left(T\right)\right)={\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)}^2{p}_1-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)p_2-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)p_3+p_4+p_5-\left(t^{\frac{5}{2}}+t^{\frac{1}{2}}\right)p_6$。

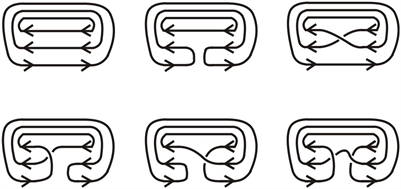
Figure 10. Link $C\left({\chi }_i\right)\left(i=1,2,\cdots ,6\right)$

图10. 链环 $C\left({\chi }_i\right)\left(i=1,2,\cdots ,6\right)$

定理4.3链环 $C\left({\epsilon }^{2k}\right)$ 的Jones多项式为

$V\left(C\left({\epsilon }^{2k}\right)\right)={\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)}^2{\alpha }_{1_k}-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right){\alpha }_{2_k}-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right){\alpha }_{3_k}+{\alpha }_{4_k}+{\alpha }_{5_k}-\left(t^{\frac{5}{2}}+t^{\frac{1}{2}}\right){\alpha }_{6_k}$。

证明：由定理4.1有 $V\left({\epsilon }^{2k}\right)={\displaystyle \underset{i=1}{\overset{6}{\sum }}{\alpha }_{i_k}}V\left({\chi }_i\right)$。再由定理4.2可得

$V\left(C\left({\epsilon }^{2k}\right)\right)={\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right)}^2{\alpha }_{1_k}-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right){\alpha }_{2_k}-\left(t^{-\frac{1}{2}}+t^{\frac{1}{2}}\right){\alpha }_{3_k}+{\alpha }_{4_k}+{\alpha }_{5_k}-\left(t^{\frac{5}{2}}+t^{\frac{1}{2}}\right){\alpha }_{6_k}$。

5. 结语

本文主要讨论了一类3-缠绕的Jones多项式。通过Giller的房间理论给出两个3-缠绕的复合的Jones多项式。其次，给出一类特殊3-缠绕的Jones多项式计算公式，并在此基础上计算了3-缠绕闭包方法得到的链环的Jones多项式。