1. 引言
工程结构优化设计最早采用的是基于直觉的准则法,根据工程经验和力学概念预先建立某种准则,经过相应的迭代,得到满足准则的设计方案作为问题的最优解,但该方法缺乏理论依据。1960年,Schmit [1] 将数学规划引入到优化算法中,但该方法受工程规模限制,计算效率低。传统的建筑结构优化方法受人为主观因素较大,对于复杂的结构优化不仅费时费力,得到的优化结果也不太理想。该方法已逐渐不能满足装配式建筑行业的发展需要 [2]。随着科学技术的发展,智能优化算法的出现,为人们解决结构优化问题提供了新思路,自动建模优化分析减少了主观因素的影响,能有效提高结构优化设计效率。运用优化算法进行优化设计越来越受到不同领域学者们的重视,特别是在建筑结构优化问题方面 [3]。当前建筑结构优化设计过程仍存在性能分析不足、外部抗剪力与内部刚度相矛盾的问题,基于此,探讨建筑结构优化设计至关重要 [4]。
结构优化设计属于一种离散变量的优化设计问题,结构优化的目的是在满足结构稳定性的要求下,对结构做出最安全经济的设计。以所需要满足的要求作为约束条件,以截面尺寸或者结构外形等作为设计变量,以结构性能指标或者造价作为目标函数,建立可进行最终优化的数学模型,运用智能算法对数学模型进行求解。实践证明,工程结构优化设计可以有效提高设计水平与工程质量,优化后的设计方案降低了造价成本。
2. 结构优化层次
2.1. 尺寸优化
尺寸优化是对结构各组成构件的截面尺寸进行优化,以达到降低结构重量或降低造价成本的目的。设计变量可以是杆的横截面积、板的厚度等,目前尺寸优化已经比较成熟。
2.2. 形状优化
形状优化通过调整结构内外边界的形状以此达到改善结构性能的目的,主要对杆系结构和连续体结构进行优化设计,设计变量可以是结构外形或者边界节点集。
2.3. 拓扑优化
拓扑优化重点对连续体结构和离散结构进行拓扑优化,主要是通过对材料分布进行拓扑优化以此得到最优分布方案的目的,主要包括变密度法、渐进结构法和均质法三大类。
3. 建筑结构优化设计
常见的建筑结构有框架结构、剪力墙结构、桁架结构。根据不同的划分标准,可将建筑建构划分为好几种类型。按照结构的受力体系进行划分,划分后的建筑结构类型的优缺点、应用范围及其代表性建筑如表1所示。
3.1. 框架结构优化
框架结构是混凝土建筑中的一种常用的结构形式,由于其传力明确、布置灵活而被广泛应用。近年来,已有大量学者对框架结构进行智能优化设计研究。王学兵 [5] 采用遗传算法对槽门框架结构进行优化,减轻了槽门框架的自重。Gholizadeh [6] 采用蝙蝠算法对钢框架结构进行优化,通过优化结构尺寸,降低了框架结构的总质量。何嘉年 [7] 采用遗传算法对半刚性连接钢框架结构体系进行优化设计,提高了结构优化设计的效率,并且使结构构件更能充分发挥作用。楼善治 [8] 等人采用自适应遗传算法对混凝土框架结构进行优化设计提高了构件尺寸优化效率,降低了造价成本,优化过程中整体结构的造价下降曲线如图1所示。
杨鎏 [9] 等人与何浩祥 [10] 等人分别采用混合智能算法对弯剪型框架结构和框架结构进行优化设计,均提高了计算效率,为均匀变形的结构优化设计提供了参考。ÇARBAŞ [11] 和李沛豪 [12] 分别采用生物地理学的优化算法和改进粒子群算法对钢框架结构进行优化,前者有效降低了钢框架结构的材料总成本,后者表明改进后的粒子群算法可应用于钢框架抗震优化设计。Gholizadeh [13] 基于改进的海豚回声定位算法对钢框架的抗震布局进行优化,发现在布局优化过程的结构配置比纯尺寸优化所获得结构配置轻约10%。朱朝艳 [14] 等在强度约束、构造约束等约束条件下,应用改进的遗传算法对框架结构进行优化,结果表明,可有效降低框架结构的总造价,应用于框架结构的优化设计中效果良好,为建筑结构优化设计提供了一种新思路。对上述学者所进行的框架结构优化设计进行分析总结,如表2所示。

Figure 1. Cost curve of structural optimization process
图1. 结构优化过程造价曲线

Table 2. Optimum design of frame structure
表2. 框架结构优化设计
综上所述,各学者对框架结构进行智能优化设计,运用智能算法相比于常规的设计方法可以有效提高设计效率,可减轻结构的总质量和降低材料的总成本。并且优化后的效果良好。虽在框架结构工程中应用算法进行优化设计的研究较多,但运用智能算法对框架结构抗震优化设计的研究较少。
3.2. 剪力墙结构优化设计
剪力墙结构具有很好的承载力和整体性,在高层建筑中得到广泛应用。胡佳俊 [15] 通过改进自适应遗传算法与有限元软件相结合的方法对剪力墙结构进行延性性能优化设计,确定了优化参数,使结构具有了优秀的延性。Saedi [16] 通过改进海豚回声定位算法来实现对剪力墙结构优化设计,此方法使得剪力墙结构重量减轻了10%。林树宏 [17] 通过改进遗传算法对钢板剪力墙结构进行优化,降低了常规布置方案结构的自重,材料性能得到最大限度的利用Kaveh [18] 采用三种典型的智能算法对钢板剪力墙的尺寸和性能进行优化设计,结果表明优化效果良好。黄韵兴 [19] 基于改进的遗传优化算法以结构位移为目标函数对钢板剪力墙进行优化,对优化后的剪力墙进行试验研究,结果表明,可有效提高剪力墙结构体系的承载力和耗能能力等。Talatahari [20] 基于量子带电系统搜索算法对高层建筑剪力墙布局进行优化设计,以高层建筑的成本为目标函数,考虑了结构和建筑要求,可有效减少高层建筑的成本。卢巧玲 [21] 通过微粒群优化算法对剪力墙位置进行优化,为降低抗震体系的动态反应,满足抗震要求,具有理论意义,优化后最佳位模态图如图2所示。
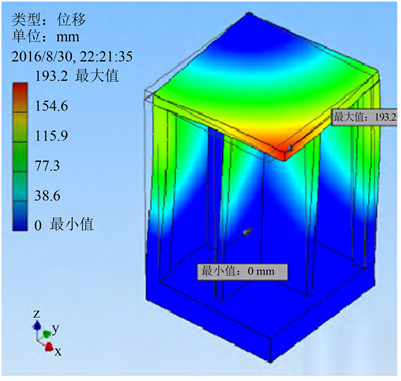
Figure 2. Optimum position F1 = 147.81 Hz modal diagram
图2. 最佳位F1 = 147.81 Hz模态图
李彬 [22] 对剪力墙结构中的剪力墙布置优化进行研究,通过改进的遗传算法以剪力墙总长度最小为目标函数进行剪力墙结构布置优化搜索,研究表明,优化后的方案满足结构规范并能取得良好的经济效果。对学者们所进行的剪力墙结构优化设计分析总结如表3所示。

Table 3. Optimal design of shear wall structure
表3. 剪力墙结构优化设计
综上所述,对剪力墙结构进行优化设计时,主要对参数进行优化或者通过优化来减轻结构的自重,使材料性能得到最大限度的应用。基于优化算法对剪力墙结构的优化设计研究比较少,运用优化算法对剪力墙结构抗震优化设计时,相应目标函数中的参数确定尚需进一步挖掘和完善。
3.3. 桁架结构优化设计
桁架结构简单,布置比较灵活,能够承载多方向的荷载,被广泛应用于多种领域。目前对运用智能算法对桁架进行优化设计的研究越来越多,李梦欢 [23] 采用智能算法与人工神经网络技术相结合的方法对平面桁架结构和空间桁架结构进行截面优化,结果表明此方法可大大节省计算耗时,且能稳定收敛,具有很好的适用性。覃俊霖 [24] 提出一种改进的布谷鸟搜索算法用于优化桁架尺寸问题,并且可在尺寸优化基础上转化为形状优化,优化结果表明,该方法可以有效解决桁架结构的尺寸优化问题和形状优化问题。Baghlani [25] 提出一种与萤火虫算法杂交的新型可行边界搜索技术,是一种桁架结构尺寸中的约束处理技术,可快速得出桁架结构重量优化方案。Jalili [26] 提出一种迁移和差分演化相结合的策略算法,对多频率约束桁架结构进行优化设计,基于基准桁架设计实例与现有优化技术进行比较,验证了该方法的有效性。Kaveh [27] 采用入侵杂草优化算法和洗牌蛙跳算法的高效混合优化算法对桁架截面尺寸进行优化设计,该方法得到了收敛更好的解决方案,并且减少了结构分析数量。百丽丽 [28]、李沛豪 [29]、康俊涛 [30] 和王宇沿 [31] 运用不同的优化算法分别对静定13杆桁架结构、52杆桁架结构、600杆圆顶状空间桁架结构和1410杆双层网壳桁架结构进行优化设计,以结构取得最小重量为优化目标,桁架截面面积为优化变量,验证了算法对于桁架结构优化设计的适用性,由此说明不论是13杆桁架还是大规模的桁架结构优化算法都适用。1410杆双层网壳桁架结构如图3所示。

Figure 3. 1410 pole double-layer lattice shell truss structure
图3. 1410杆双层网壳桁架结构
对学者们所进行的桁架结构进行优化设计分析总结如表4所示。
综上所述,对桁架结构进行优化设计主要围绕桁架尺寸进行优化,各学者通过运用不同的智能算法或与对算法进行改进、组合等,可以很好的解决桁架尺寸优化的问题,验证了算法的适用性。同时也可以快速有效的得出重量优化方案,减轻桁架自身重量,验证了算法的有效性。目前运用智能算法对桁架尺寸进行优化的研究比较多,而对桁架进行形状优化的研究比较少,因此后续应深入对桁架形状优化领域的研究。
4. 结论
近年来,我国多次发生不同等级的地震,对建筑结构的安全性能要求不断提高,结构设计是否合理对建筑结构的整体可靠性起着至关重要的作用。运用智能优化算法对结构进行优化设计,可以有效提高结构设计效率,减少人为因素对优化结果的影响。对于复杂的结构进行优化,传统的智能算法有时不能达到很好的优化效果,可对优化算法进行改进、组合或者与有限元软件相结合。研究高效的结构优化方法对建筑行业的发展具有重要的意义,本文介绍了智能算法在框架结构、剪力墙结构、桁架结构优化设计的应用,为智能算法在更多领域的结构优化的应用提供参考。
基金项目
河北省自然科学基金资助项目(E2020402079);河北省高等学校科学技术研究项目(ZD2019114)。