1. 引言
2020年数据调查得出,我国乳腺癌发病人数约为42万,并且这一数据有持续上升的趋势。其中对女性而言,这是发病率高居榜首的恶性肿瘤。作为一种激素依赖性肿瘤,乳腺癌发生、发展与癌细胞上的雌激素受体的表达密切相关 [1]。根据病理分型,大约70%的乳腺癌患者是雌激素受体(ER)阳性,这其中有研究发现,雌激素受体α亚型(Estrogen receptors alpha, ERα)在不超过10%的正常乳腺上皮细胞中表达,但大约在50%~80%的乳腺肿瘤细胞中表达,ER的异常表达促进乳腺癌的发生及发展。因此临床中抗激素治疗常被用于ERα表达的乳腺癌患者,这一方法是通过调节雌激素受体活性来控制体内雌激素水平。因此,ERα是乳腺癌发展的关键调节因子是治疗乳腺癌的重要靶标,能够拮抗ERα活性的化合物可能是治疗乳腺癌的候选药物。
高昂的研发费用和漫长的周期延缓了新药的开发进展,因此,具有高效率和低成本的化合物活性预测模型是筛选潜在活性化合物的有效方法。成功的模型能够预测具有更好生物活性的新化合物分子,或者指导已有活性化合物的结构优化。一个具有良好的生物活性(此处指抗乳腺癌活性)和在人体内具备良好的药代动力学性质和安全性的化合物可以成为良好的候选药物,这两大特性被通称为ADMET (Absorption吸收、Distribution分布、Metabolism代谢、Excretion排泄、Toxicity毒性)性质。预测和评价ADMET 药物动力学方法是目前药物设计和筛选中一种非常有效的手段 [2],早期分析能够减少药物开发后期的风险,还能为筛选最优化合物提供强有力的理论依据。其中,ADME主要指化合物的药代动力学性质,描述了化合物在生物体内的浓度随时间变化的规律,T主要指化合物可能在人体内产生的毒副作用。合格的候选药物至少要满足化合物活性好、易吸收、易排泄代谢速度适中、对人体无毒性等特征,否则很难成为药物,还需要对其进行ADMET性质优化。
基于上述研究背景,本文需研究和解决以下问题:选择不超过20个分子描述符变量,构建化合物对ERα生物活性的定量预测模型,叙述建模过程。然后使用构建的预测模型,对50个化合物进行IC50值和对应的pIC50值预测。即对样本数为1974的化合物分子描述符和pIC50进行分析,以根据两者之间的关系,构建预测模型,并对新样本进行pIC50的预测。采取BP神经网络的方法,对数据进行“训练”及“累积”,尽可能多的将分子描述符和pIC50之间的关系进行高度非线性映射,并完成预测工作。为更有效地解决问题,提出以下模型假设:
① 假设分子描述符与生物活性和ADMET之间具有一定的线性和非线性关系。
② 忽视本文所选取分子描述符之外的因素对问题产生的影响。
③ 不考虑分子描述符相互之间的影响。
④ 不考虑分子描述符对线性或非线性关系的影响。
2. 理论基础
在机器学习和认知科学中,人工神经网络是借助生物神经网络原理的一系列数据性学习模型,如动物中枢神经系统,尤其是脑系统。根据Kolrnogov定理,1个3层的神经网络能够实现对任意非线性函数进行逼近。因此,BP神经网络具有很强的非线性映射能力。使用上述选择的分子描述符和pIC50,使用能以任意精度逼近的BP神经网络模型,建立ERα生物活性定量预测模型,并进行预测。模型输入数据为nHBAcc、nHBint6等10个分子描述符数据;输出数据为pIC50,建立的神经网络结构如图1所示。其中x1~x10是人工神经元的输入信号,即分子描述符;wij表示链接强度,即从神经元j到神经元i链接权值,正值为激活,负值为抑制;求和单元将输入信号进行线性组合;函数为转移函数(Transfer Function)或激活函数(Activation Function),以控制神经元输出幅度,一般在(0,1)或(−1,1)之间;θi表示阈值(threshold)或偏置(bias),两者为相反数。

Figure 1. Artificial neural network structure
图1. 人工神经网络结构
以上可以通过数学表达式展示输入y与输出x的关系:
(1)
式中,
表示输入信号;
表示神经元i的权值;
θ为阈值;
yi为神经元i的输出。
常用的激活函数有:线性函数、斜坡函数、阈值函数、S (Sigmoid)型和双极S型函数。该模型选择α = 2的双极S型激活函数,即:
(2)
BP (Back Propagation)神经网络是一种前馈神经网络,即信号向前,误差向后传播。信号传播过程如下图2所示,一个神经网络通常包含三层,第一层为输入层,第二层为隐含层,第三层为输出层。
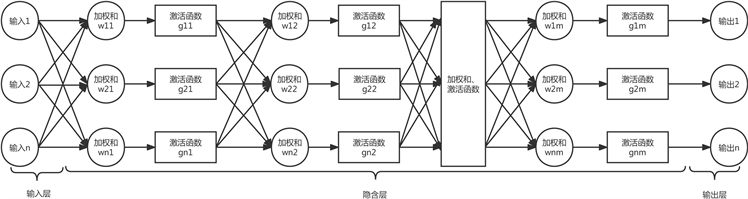
Figure 2. Neural network propagation path
图2. 神经网络传播路径
3. 研究设计
利用BP神经网络建立分子描述符与生物活性的非线性函数关系。具体流程如下图3所示。
首先对要参与预测的分子描述符进行标准化处理,然后选取莱文贝格–马夸特方法(Levenberg-Marquardt)和量化共轭梯度法(Scaled Conjugate Gradient)分别尝试10次,并在实验前从原始数据中抽出最后10个数据来判断拟合度R2,找出拟合度较高且均方误差较少的那次实验的数据作为本次的预测模型。

Figure 3. BP neural network operation flow chart
图3. BP神经网络操作流程图
通过误差对比,确定最佳的隐含层神经元个数,拟合误差运行结果如表1所示。
图4表明,在经过17次训练后,隐含层神经元为11个的BP网络对函数的逼近效果最好,误差最小。因此,预测模型选择神经元个数为11。
通过10次模拟,对照选取的10个样本所对应的生物活性的预测值与真值的差异性,找出拟合度最高的训练方法和结果,最终得到的拟合结果如图5所示,R²均在0.7以上,拟合度较高,结果具有一定的可信度。由于pIC50是IC50的负对数转化来的,通过推导,其运算公式为:
(3)
使用上述构建的预测模型,对文件“ERα_activity.xlsx”的test表中的50个化合物进行IC50值和对应的pIC50值进行预测后,同时将结果填入了“ERα_activity.xlsx”的test表中的IC50_nM列及对应的pIC50列,部分结果展示如表2所示。

Table 2. Predicted bioactive IC50 and pIC50 results
表2. 预测的生物活性IC50和pIC50结果
4. 模型总结与评价
模型的优点在于:基于MATLAB模型的神经网络模型可以模拟多变量而不需要考虑对象复杂的不确定性和时变性,容易建立预测模型,从而较为精确的预测变量之间的映射关系[3]。
模型的缺点在于:训练集、验证集、测试集的比例Matlab会后台自动选择比例来随机抽取样本,因此每次运行的结果可能都不相同。
参考文献
附录
运用 Matlab 中的神经网络求解,由于IW1_1输出数据过多,故仅显示前五个作为代表,其代码如下:
function [Y,Xf,Af] = myNeuralNetworkFunction(X,~,~)
%输入1
x1_step1.xoffset =
[-0.959;-0.28044;-2.13884;-6.21238;-4.95147;-0.86629;-0.9518;-0.81305;-0.3341;-2.3047];
x1_step1.gain =
[0.0813653761033145;0.0653666119112348;0.353827618722435;0.107571703263457;0.313105663768352;0.393439011051702;0.110856141984547;0.205235559112972;0.185961574759807;0.497050008201325];
x1_step1.ymin = -1;
% 层次 1
b1 =
[-1.8111078060248325;1.4282247551582381;-0.90375982196551596;-0.43482491375879534;-0.14148385537068167;-0.36312851996008744;-0.72403667783393577;-1.1031963793364412;1.4281464859036888;1.7488087416098097];
IW1_1 = [0.76888607300302514 0.057461449570589615 0.22616072432086912 0.2389943344597017-0.45858207366829273 ……];
% 层次 2
b2 = -0.56306330953903883;
LW2_1 = [-0.6941891684317768 0.20237767688952646 0.85292026637443752 0.22063298452340385 -0.10509355479025818 0.63502770960891264 0.63730818276650569 -0.30593569017895728 0.10969211004056961 -0.012179211610543887];
% 输出 1
y1_step1.ymin = -1;
y1_step1.gain = 0.253774901662226;
y1_step1.xoffset = 2.456;
% 格式输入参数
isCellX = iscell(X);
if ~isCellX
X = {X};
end
% 求解矩阵大小
TS = size(X,2);
if ~isempty(X)
Q = size(X{1},1);
Q = 0;
end
%分配输出
Y = cell(1,TS);
% 循环
for ts=1:TS
% 输入 1
X{1,ts} = X{1,ts}';
Xp1 = mapminmax_apply(X{1,ts},x1_step1);
% 层次 1
a1 = tansig_apply(repmat(b1,1,Q) + IW1_1*Xp1);
% 层次 2
a2 = repmat(b2,1,Q) + LW2_1*a1;
% 输出 1
Y{1,ts} = mapminmax_reverse(a2,y1_step1)Y{1,ts} = Y{1,ts}';
end
% 最后的延迟状态
Xf = cell(1,0);
Af = cell(2,0);
% 格式输入参数
if ~isCellX
Y = cell2mat(Y);
end
end
%映射最小和最大输入处理功能
function y = mapminmax_apply(x,settings)
y = bsxfun(@minus,x,settings.xoffset);
y = bsxfun(@times,y,settings.gain);
y = bsxfun(@plus,y,settings.ymin);
end
% 对称传递函数
function a = tansig_apply(n,~)
a = 2 ./ (1 + exp(-2*n)) - 1;
end
% 映射最小和最大输出的逆向处理功能
function x = mapminmax_reverse(y,settings)
x = bsxfun(@minus,y,settings.ymin);
x = bsxfun(@rdivide,x,settings.gain);
x = bsxfun(@plus,x,settings.xoffset);
end