1. 引言
随着科技的飞速发展,“无人机”作为新时代具有代表性的智能科技产品,在军事和民用方面地位日渐凸显,被广泛运用。高效、平稳完成任务是无人机发展的基本要求,路径规划作为其关键技术之一,备受学者们关注。目前,无人机的路径规划算法主要分为两类,一类是基于图搜索路径的传统算法,如:Dijkstra算法 [1],人工势场法 [2]、A*算法 [3] 等,该类算法在简单的地图环境中进行路径规划优势突出;另一类是基于仿生学智能搜索路径的智能算法,如:遗传算法 [4]、蚁群算法 [5]、飞蛾扑火算法 [6] 等,该类算法主要用于复杂的地图环境。
蚁群算法具有鲁棒性强,正反馈机制等优点,被广泛用于解决路径规划问题 [7] [8] [9]。但该算法也存在收敛速度慢和易陷入局部最优等缺点。针对该算法存在的问题,一部分学者从蚁群算法自身出发,优化其搜索策略及模型。袁梦顺 [10] 等人引入双精英蚁群策略和混沌扰动思想,对信息素更新策略进行优化,将引力场和斥力场赋予目标点和障碍物,为无人机航迹搜索指导方向。马小陆 [11] 等人利用万有引力搜索策略,解决蚁群算法初期信息匮乏问题,提高算法收敛速度,增强全局搜索能力。陈琴 [12] 等人将禁忌搜索算法的思想融入蚁群算法,弥补其不足,提升算法运行效率,在大规模无人机调度方面优势突出。蒲兴成 [13] 等人利用引入分组教学思想,通过精英和普通蚁群的划分,优化蚁群算法中的适应度函数,提高收敛速度,改善全局规划能力。另一部分学者将蚁群算法与已有的其他智能搜索算法进行融合,弥补蚁群算法的劣势。胡致远 [14] 等将人工鱼群算法融入蚁群算法,进行优势互补,对信息素更新方式重新进行设计,优化蚂蚁搜索策略。魏立新 [15] 等人将DWA算法与蚁群算法相融合,通过GRRT-Connect算法对初始信息素进行差异分配,优化搜索方向,减少局部最优。俞佳慧等人 [16] 采用贝叶斯网络对蚁群算法中的转移概率进行优化设计,提高无人艇的避障能力。刘雨青 [17] 等人运用Dijkstra算法优化初始信息素分配模式,构造新的启发函数,适用于复杂环境下水下无人机的路径规划。杜力 [18] 等人针对蚁群算法过度依赖参数选择问题,引入萤火虫算法,自适应地为蚁群算法选择参数,减少迭代次数,提高算法精度。
上述研究一定程度上对蚁群算法进行了优化,但其收敛速度慢,易陷入局部最优的缺点难以消除。为满足无人机在有效避免危险区域的前提下,可以最快从初始点到达目标点,高效完成任务,本文在蚁群算法的基础上引入和声搜索算法,利用和声搜索算法和声扰动产生新和声的思想,增加蚁群算法前期路径选择的多样性,保留路径距离最短和声,进而对优化后的路径进行信息素更新,从而提高收敛速度,减少局部最优情况。通过路径平滑处理,缩短路径距离,减少无人机拐弯频次,提高飞行稳定性。最后,用仿真实验证明该算法的有效性。
2. 基本算法
2.1. 传统蚁群算法
蚁群算法(Ant Colony System)是由意大利学者Dorigo、Maniezzo等人于20世纪90年代对蚂蚁觅食行为进行观察研究得到启发提出的 [19] [20]。从巢穴到食物源,单只蚂蚁行为具有随机性,但群体却总能找到最短距离,表现出了一定的智能性。初始阶段,蚁群觅食体现的是单只蚂蚁行为,随机选择路径,但蚂蚁可以在经过的路径上分泌一种特殊物质,蚁群中的蚂蚁对这种物质具有感知能力。这种特殊物质后来被称为“信息素”。在选择路径时,后面的蚂蚁会趋向于选择信息素浓度较高的路径。虽然“信息素”会随着时间逐渐挥发,但距离短的路径,留下的“信息素”浓度较大,蚂蚁选择此路径的概率就会增大,进而留下的“信息素”更多,浓度更大,这就形成了一种正反馈机制,最终找到达到食物源的最短路径。基本流程如下:
1) 初始化参数
对蚁群算法的参数进行初始化,包括蚂蚁数量m、信息素因子a、启发函数因子β、信息素挥发因子ρ、信息素常数Q、最大迭代次数t等。
2) 构建解空间
将各个蚂蚁放置在初始点,对于每个蚂蚁k(
),计算下一个待访问节点,直至每个蚂蚁都到达终点或者进入死胡同。
蚂蚁在选择路径过程中,采用轮盘赌法选择下一个要到达的节点。选择每一段路径的概率为:
其中,i、j分别表示每段路径的起始点和终点,τ表示在时间t时,由节点i到节点j所形成的路径上的信息素浓度,η表示t时节点i到节点j所形成的路径距离d的倒数,
表示未访问过的节点的集合。根据当前路径ij上的信息素浓度以及启发式函数,便可确定从起始点i选择终点j的概率。两节点的路径距离越短,信息素浓度越大,路径被选择的概率越大。
3) 更新信息素
信息素一方面随着时间的延长会挥发减少,另一方面会由新的蚂蚁途经而增加。信息素更新的表达式为:
其中,
ρ为信息素挥发因子,
是蚂蚁k路过ij路径后留下的信息素浓度,信息素一定,路径越短,留下的信息素浓度越高。
4) 判断是否达到终止条件
蚁群算法的终止条件是:判断是否达到最大迭代次数。
2.2. 和声搜索算法
和声搜索算法(Harmony search, HS)是由韩国学者Geem Z W等人受音乐创作启发,提出的一种智能优化算法 [21]。该算法的基本思想是:把多个原有和声看成和声库,随机抽取原有和声,对和声的音调进行调整,产生新和声,将新和声与和声库中最差和声进行比较,如果新和声更好,则新和声替换和声库中的最差和声,反复调整,直到形成美妙和声。一般HS算法步骤如下:
1) 设定问题和参数
a) 设定问题为最小化问题,即:
。
为目标函数,x是由决策变量
形成的解向量(
),每一个决策的值域为
。决策变量可以为离散型:
,也可以为连续型变量:
。
b) 初始化参数:对和声搜索算法的参数进行初始化,包括和声记忆库大小HMS、抽取和声记忆库概率HMCR、音调微调概率PAR、音调微调带宽BW、创作的次数Tmax等。
2) 初始化和声记忆库HMS
在解空间中随机生成HMS个和声存入和声记忆库,并对其进行记录:
3) 生成一个新的和声
抽取和声记忆库中的和声,对和声的音调进行扰动处理产生新和声
,扰动处理有三种方式:① 学习和声记忆库,② 音调微调,③ 随机选择音调。
4) 更新和声记忆库
通过目标函数对新和声的优劣进行评估,即:与HM记忆库中目标函数值最差的和声进行比较,若新和声更优,则替换最差和声,更新和声记忆库。
5) 检查算法是否终止
重复步骤(3)和(4),直到迭代次数达到Tmax为止。
3. 改进的蚁群算法
传统蚁群算法收敛速度慢,易陷入局部最优,路径拐点所,不利于无人机高效、稳定地完成任务。针对以上问题,本文引入和声搜索算法改进蚁群算法,即在蚁群完成一次搜索路径后,通过和声搜索算法对路径进行优化,提高算法收敛速度,减少局部最优。另一方面,搜索路径中会出现多个拐点,本文对路径进行平滑处理,删除不必要节点,缩短路径距离,提高搜索效率。
3.1. 基于和声搜索改进的蚁群算法
蚁群算法收敛速度慢的一个原因是前期蚂蚁主要是随机选择路径,路径效果较差。本文引入和声算法,利用和声算法优化解空间的方式提高蚂蚁算法的收敛速度。其基本思路为:
1) 蚂蚁从初始点开始,按照蚁群算法的步骤进行路径选择,每一轮迭代中的全部蚂蚁路径搜索结束后引入和声搜索算法,对这一代的路径结果进行优化。每只蚂蚁选择的路径为一个和声,路径中的节点为和声粒子,所有达到终点的蚂蚁选择的路径结果作为和声搜索算法的初始解,形成和声记忆库。
蚂蚁m路径搜索结束后形成的路径信息为:
。取M只蚂蚁中达到终点的蚂蚁所走路径,形成和声搜索算法的和声记忆库,为:
与传统和声搜索算法不同的是本文中形成的和声记忆录库,每一个和声的和声粒子数目不一定相等,其取决于蚂蚁到达终点经过的节点个数。和声搜索算法的目标函数为蚂蚁从出发点到终点的路径距离。
2) 抽取和声记忆库,通过和声扰动算法对和声粒子进行扰动,形成新的和声粒子,与原和声记忆库进行比较,如果路径更优则保留,更新和声记忆库。否则,保留原和声记忆库。
传统和声搜索算法和声扰动通常采用的是微调或者随机产生音调的方法,本文和声扰动采用的是相邻领域变异的方法,指的是在当前节点相邻领域的栅格中抽取可达的栅格作为新的和声粒子。如图1所示,和声粒子A相邻领域有8个,经过和声扰动可变异的音调理应有8种可能结果,由于右方不可达,扰动后的新音调实际有7种结果,从这7种新音调中进行随机抽取。抽取后的新音调与其他音调构成了新和声,将新和声路径与和声记忆库中的其他和声进行比较。
3) 对和声记忆库中的路径进行蚁群信息素更新,迭代,直到达到终止条件。
3.2. 路径平滑处理
蚁群算法易陷入局部最优,出现多个拐点,多拐点会导致无人机频繁转换方向,影响平衡控制。其次,多拐点的路径一定不是最优路径。如何对路径进行平滑处理是不容忽视的问题。本文基于两点之间直线距离最短基本原理,删除不必要的节点,在合理避障的前提下,用直线距离代替多拐点路线。
本文采用迭代法的方式,从第一个节点开始,按顺序探索删除与其连接节点的可能性,无法避障或者达到终点时停止此节点的探索,然后迭代下一个节点,直到所有节点被迭代完成。以第2个节点为例,如图2所示,首先考虑删除第3节点,从第2节点直接到第4节点,未经过障碍物,且路径距离减小,如图3所示;接着,考虑删除第4节点,从第2节点直接到第5节点,如图4所示;以此类推,删除第5节点,如图5所示;删除第6个节点,从第2节点直接到第7节点,此条路径有障碍物阻挡,不可行,如图6所示。因此保留第6节点,删除3、4、5节点,最终保留路径如图5所示。
判断上一节点到下一节点是否跨过障碍物,本文以节点所形成的矩阵为考察区域,区域内的所有障碍物均须被判断是否阻碍两个节点的连接。两个节点的连线与障碍物的最短距离大于栅栏对角线长度的一半,表明未跨过障碍物。如图7所示,判断节点A到节点B是否需要跨过障碍物,需考察A和B形成的矩阵区域内的障碍物,即黄虚线所构成的区域。区域内含有障碍物1~6,以障碍物5为例进行判断,计算障碍物5中心点到AB的最短距离d,若d > 栅格单位长度对角线的一半,说明从A节点到B节点没有经过障碍物5,同理,判断障碍物1、2、3、4、6。当A节点到B节点均不跨过障碍物1~6时,则表明A节点直线到达B节点没有跨过障碍物,即在避障情况下直线可行,否则,不可行。
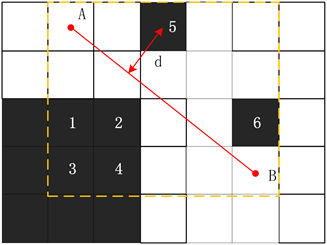
Figure 7. Schematic diagram of judging whether the node connection crosses an obstacle
图7. 判断节点连线是否跨过障碍物示意图
3.3. 算法实现流程
基于和声搜索改进的蚁群算法的主要步骤有:
步骤1:初始化参数,设置最大迭代次数K、蚂蚁数量M、信息素因子a、启发函数因子β、信息素挥发因子ρ、信息素增强系数Q等;建立栅格环境,标记初始点位置和终点位置。
步骤2:寻找解空间,将蚂蚁放置于初始位置,采用轮盘赌法选择蚂蚁下一步可以达到的节点,使用禁忌表记录不可达节点和蚂蚁走过的节点,蚂蚁走到终点或者陷入死胡同则停止,记录每一次迭代每只蚂蚁的觅食路线和路线距离。
步骤3:初始化和声搜索算法参数,将到达终点的蚂蚁路径作为初始和声记忆库,路径中的每一个节点作为和声粒子,设置从和声库取出一个和声的概率hmcr,设置相邻领域变异扰动的取值范围BW,和声搜索迭代的最大次数Tmax。
步骤4:和声搜索算法通过和声扰动优化解空间,根据hmcr从和声记忆库抽取和声,对抽取的和声粒子进行相邻领域扰动处理,生成新的和声。找出当前记忆库最差的和声,与新和声进行比较,如果新和声路径距离比和声记忆库最差的和声的路径距离更短,则新和声替换最差和声,更新记忆库,否则保留原和声记忆库,迭代Tmax次。
步骤5:更新信息素,对顺利到达终点的蚂蚁路线进行信息素更新。
步骤6:路径平滑处理,删除不必要节点,减少拐点,优化路径。
步骤7:判断是否达到迭代次数,若达到,则输出最优路径,否则转入步骤2。
算法流程图如图8所示:
4. 算法仿真分析
本文使用栅格图进行环境建模,黑色填充代表障碍物,无人机无法通过,白色填充为可通过区域,无人机从栅格图的左上角出发,右下角为终点。使用MATLAB R2018a软件平台进行仿真模拟。环境分别设置为20 × 20、30 × 30、40 × 40规模的栅格图,算法的具体参数设置如表1。

Table 1. Experimental parameter setting
表1. 实验参数设置
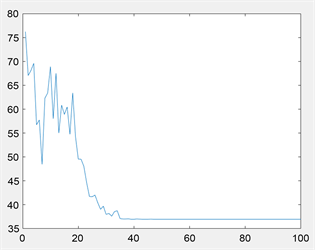
在20 × 20栅格图环境中,无人机采用传统蚁群搜索算法与基于和声搜索改进的蚁群算法仿真运动路径如图9所示,收敛曲线如图10所示。在进行无人机路径规划中,使用传统蚁群算法,经历了34次迭代,最小路径趋于平稳,路径距离为36.9706,拐点为14。相同的路障环境下,使用基于和声搜索改进的蚁群算法进行路径规划,经历18次迭代,最小路径趋于平稳,路径距离为31.1704,拐点为3。路径距离缩短5.8002,占比15.7%,收敛速度加快,拐点数量减少。
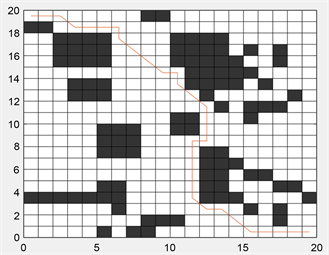 (a) 传统蚁群算法
(a) 传统蚁群算法 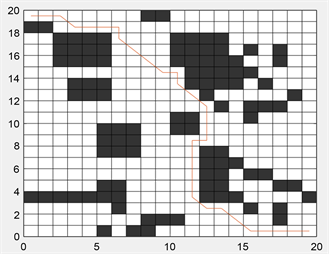 (b) 基于和声搜索改进的蚁群算法
(b) 基于和声搜索改进的蚁群算法
Figure 9. 20 × 20 grid environment simulation motion path
图9. 20 × 20栅格环境仿真运动轨迹路径
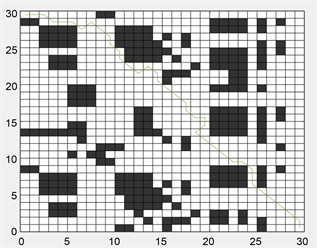
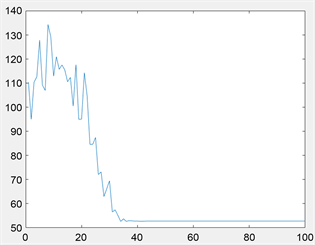
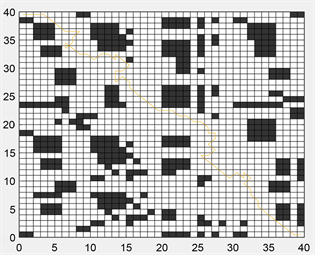
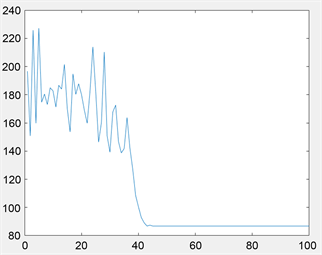
为进一步验证基于和声搜索改进的蚁群算法的有效性,本文将环境调整为更为复杂的30 × 30栅格图以及40 × 40栅格图环境进行仿真,仿真结果如图11~14所示。在30 × 30栅格图环境,传统蚁群算法最小路径距离为52.7696,基于和声搜索改进的蚁群算法路径距离缩短为43.8453,缩短16.9%;40 × 40栅格图环境中,路径距离由86.8112缩短至56.5655,缩短34.8%。相比于20 × 20栅格图环境,在30 × 30栅格图以及40 × 40栅格图环境中,基于和声搜索改进的蚁群算法搜索到的路径拐点数量明显减少,证明此算法在路径平滑处理方面,复杂环境中效果更为突出。其次,在前期迭代过程中,对比与传统蚁群算法,基于和声搜索改进的蚁群算法震荡幅度明显小,到路径趋于平稳的迭代次数少,说明此算法收敛性优于传统蚁群算法,在复杂环境中效果更显著。
 (a) 传统蚁群算法
(a) 传统蚁群算法  (b) 基于和声搜索改进的蚁群算法
(b) 基于和声搜索改进的蚁群算法
Figure 10. 20 × 20 grid environment convergence curve
图10. 20 × 20栅格环境收敛曲线
 (a) 传统蚁群算法
(a) 传统蚁群算法  (b) 基于和声搜索改进的蚁群算法
(b) 基于和声搜索改进的蚁群算法
Figure 11. 30 × 30 grid environment simulation motion path
图11. 30 × 30栅格环境仿真运动轨迹路径
 (a) 传统蚁群算法
(a) 传统蚁群算法  (b) 基于和声搜索改进的蚁群算法
(b) 基于和声搜索改进的蚁群算法
Figure 12. 30 × 30 grid environment convergence curve
图12. 30 × 30栅格环境收敛曲线
 (a) 传统蚁群算法
(a) 传统蚁群算法 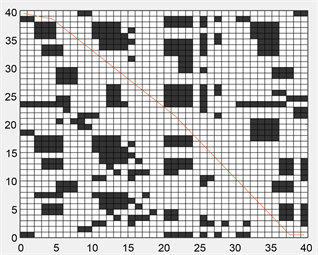 (b) 基于和声搜索改进的蚁群算法
(b) 基于和声搜索改进的蚁群算法
Figure 13. 40 × 40 grid environment simulation motion path
图13. 40 × 40栅格环境仿真运动轨迹路径
 (a) 传统蚁群算法
(a) 传统蚁群算法 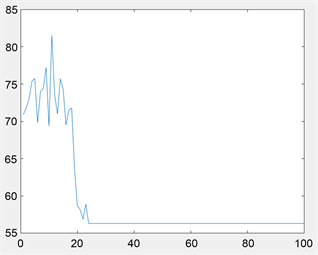 (b) 基于和声搜索改进的蚁群算法
(b) 基于和声搜索改进的蚁群算法
Figure 14. 40 × 40 grid environment convergence curve
图14. 40 × 40栅格环境收敛曲线
通过仿真模拟验证,本文提出的基于和声搜索改进的蚁群算法在无人机路径规划中可行,且相比于传统蚁群算法进行路径规划,收敛速度更快,路径更优,有效缓解局部最优问题。
5. 结论
传统蚁群算法在无人机的避障路径规划问题方面,表现出了强鲁棒性等优点,但也存在收敛速度慢、易陷入局部最优、拐点多等缺点。本文提出了基于和声搜索改进的蚁群算法,将和声搜索算法融入到传统蚁群算法中,通过和声搜索算法的和声扰动,优化每一代蚂蚁选择的路径,增加算法的多样性,提高收敛速度。针对路径结果拐点多的问题进行路径平滑处理,删除不必要节点,减小路径距离,有助于对无人机运行中进行平衡控制。仿真实验证明无人机采用基于和声搜索改进的蚁群算法进行路径规划比传统蚁群算法收敛速度更快,路径更优,且在较为复杂的栅格环境中,效果更为突出。下一步的研究,将考虑动态障碍物对无人机路径规划的影响。