1. 教科书中数学文化传承研究背景
数学教科书是数学学科知识的载体,承担着展示数学知识和传承数学文化的重任,使优秀数学文化延续与创新,发挥文化的价值。基础教育课程改革教学中,文化育人更倡导渗透数学文化的教学。2021年2月起,教育部对中华优秀传统文化和革命文化进中小学课程教材进行了整体设计和科学谋划。
在中国古代就已形成了生产活动中的数学体系,算术是六艺的重要部分,有了深厚的数学文化背景,有传承数学文化的价值。在学习数学知识要重视对表层知识的学习和运用,还需深度挖掘文化的内涵,这就需要教师具有一定专业素养和教学能力。数学文化的背后蕴涵了一个民族、乃至一个国家、一切人类的文明与智慧,数学文化融入数学课堂中教科书教学具有培养学生数学核心素养、落实立德树人和传承中华文化自信的重要价值。
中华优秀传统文化根植于我国各民族的土壤中,是我国各族人民共同的精神财富。基础教育改革提出大力弘扬中华传统数学文化,在数学课程中,传承数学教科书中“数学文化”成为当代教育界热点话题之一。
2. 中华优秀传统文化与数学教材的整合价值
教科书中所传承数学文化的形式包括专题、正文、习题和其他栏目四个方面,教科书中所传承数学文化的内容有数学史、思想方法、应用以及数学美。
数学史内容的类型相当丰富,具体可以分为:“数学概念史”、“数学家介绍”、“数学历史名题”、“数学历史典故”等。数学史与教材的呈现形式以纯文本和图文并茂两种呈现方式为主。湘教版中图文并茂形式的数学史素材数量最多,湘教版注重在知识点的介绍中添加相关数学家的人物头像。湘教版形式丰富,不仅包含历史著作、相关实物图、问题情境等相关图文。在中小学数学课堂教学中融入优秀的数学文化,就是将我国优秀传统文化中的科学精神、哲学思想、教育思想、人文修养渗透数学课堂的教科书教学中,继承我国优秀传统文化的基因,培育学生成为我国民族复兴的时代新人 [1]。
2.1. 增加学习数学的动机,勇于质疑、探索、创造的科学精神
数学是不断发展的且具有趣味性的学科,通过融入数学历史与数学教科书中,探索数学理论发生发展的过程中,融合数学理论与现实,感受数学家在探究真理中展现的人格魅力。
教科书中融入数学史素材,学生可以从数学学科本身出发,深入了解有关数学知识背后的故事,提高学习兴趣。在素材中感受数学与数学家勇于质疑、探索、创造的科学精神。作为教师,善于挖掘数学课堂上的教科书中隐藏的优秀传统文化,在中华民族优秀传统文化的熏陶下,学生对数学课堂和数学学科知识产生学习内驱力,增加学习数学动机。数学家们乐于思考,不断探索,严谨治学的精神以及对数学研究的热爱。
中国的数学家对数学发展做出了巨大的贡献的事迹一直激励着当代青年学生,培养青年学生爱国主义情感和民族认同感。让学生感受整个中华文化对数学学科领域的发展做出的伟大贡献。数学概念、定理等知识发展的背后蕴含着数学家们孜孜不倦的研究历程,有助于培养学生不畏艰难、严谨细致的学习观,以及正确的人生观、价值观。
2.2. 拓宽学生学习视野,探索宇宙奥妙和揭示其规律的哲学思想
只有依靠哲学的沉思才能全面而深刻地认识数学,哲学的滋养和关怀的使我们有深度的认识数学。数学文化哲学的孕育和产生有着深刻的学术背景和社会因素。数学因其学科交叉的性质带有浓厚的数学文化气息。数学在数学史、数学社会学与数学文化哲学等课程中是相互交叉的,数学整合数学史、数学社会学中的数学哲学思想,数学文化哲学广泛的分析数学的本质和价值。数学文化哲学,对数学的教育文化价值的研究具有特殊性。
人的观念、精神以及思维方式会受到数学文化价值的影响。数学的思维训练是养成与发展人类理性精神的有效方式,数学是间接的研究现实世界的数量关系,独立地建构研究对象的“模式”。陶冶人的美感,提高理性的审美,探索宇宙奥妙和揭示其规律的依赖于数学的思维方法。由“应试教育”向“素质教育”转变,目的是为未来培养高素质的人才。总之,教师要用发展的眼光看待数学教科书中的数学文化哲学,这对我国未来的数学教育发展与创新有着深远的意义。
2.3. 培养创造性的数学人才,弘扬中华传统文化中的教育思想
中国古代数学家李冶“术数虽居六艺之末,而施之人事,则最为切务。”他发现数学的应用价值,在讲授天元术首先从“方圆幂积”讲起,由浅入深、循序渐进。通过亲身实践来弘扬这种数学文化思想,他先进的数学文化及教育思想不仅在古代颇具影响,并且在现代数学教育教学的研究中仍有重要的指导和借鉴意义。徐利治数学教育思想可以概括为如何成为创造性的数学人才,主要有数学方法论、成才观、数学学习观、数学教学观和数学创造观 [2]。
通过特殊实例的观察、分析、归纳、推理等过程来发现、发掘新的数学真理知识。作为数学老师,要教会学生运用科学归纳法从特殊例子中去发现出一般性的东西来。徐先生认为,归纳法和类比法是发现数学真理的重要方法。激发学生内在学习动机,激励他们永远奋发向上的学习,实现高尚的人生理想。
3. 以人教版、北师大版、湘教版三版教材的初中数学文化传承研究为例
数学文化具有广泛的内涵,汪晓勤将数学文化划分为数学史、数学与现实生活、数学与科学技术和数学与人文艺术 [3]。本研究参照这个标准,分别对人教版、北师大版、湘教版三版教材的初中数学7、8、9年级,共18本教材中的数学文化进行统计,得出数学文化的总数量见图1。
三个版本的数学教材中数学文化的数量都在910个以上,其中,北师大版的数学文化数量达1000个以上,在北师大版的数学教材中体现数学文化数量是最多的,高达1179个;其次人教版的数学教材中数学文化的数量为939个,最少的是湘教版的数学教材,数量为917个。可见,三个版本的数学教材中数学文化数量十分丰富。

Figure 1. The total quantity of mathematics culture in junior middle school in the three edition textbooks
图1. 三版教材的初中数学文化的总数量置
数学文化在各年级之间的数学文化数量和内容都存在一定的差异,通过对三版教材中的数学文化进行统计,按年级的上下两册来划分,得数据见表1:

Table 1. Statistical table of grade distribution of mathematical culture
表1. 数学文化的年级分布统计表
三个版本的初中数学教材中,随着年级的增加数学文化的数量逐渐减少,七年级到八年级期间,人教版教材中的数学文化的大幅度减少;北师大版教材中,各年级之间数学文化减少的幅度也比较大;湘教版数学文化在七、八、九年级期间,数学文化依次减少,但相对而言幅度比较小。
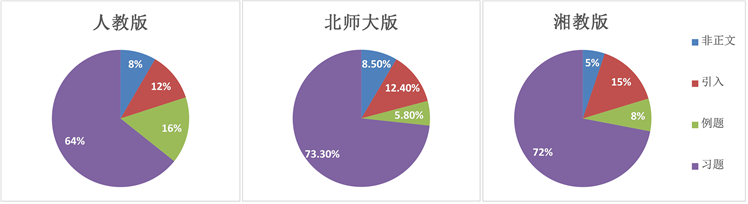
Figure 2. Column setting in textbooks of People’s Education Press, Hunan Education Press and Beijing Normal University Press
图2. 人教版、湘教版和北师大版的教材中的栏目设置
人教版、湘教版和北师大版的教材中的栏目设置各有不同,为了更好地比较三版教科书中数学文化在栏目中的分布情况,将三版教科书中的具体栏目设置统一划分为非正文部分、引入、例题、课堂练习、课后习题这五个部分,分别统计三版教材在这五个部分比例情况见图2。
我们已经从总体对三个版本教材中的数学文化进行比较研究,由于统计与概率和综合与实践部分的内容在教材中的不集中,所以,本研究选取“一元一次方程”这个知识点,在这三版教科书中,一元一次方程中的数学文化数量上存在较小的差异,但组间差异较大。数学与生活类的数学文化最多占比都为60%以上,在人教版教科书中一元一次方程这个知识点包含的数学文化是最多的,其次是湘教版,北师大版是最少的,数学与人文艺术类的数学文化在三个版本中都没有体现。一元一次方程部分的数学文化分布情况见图3。
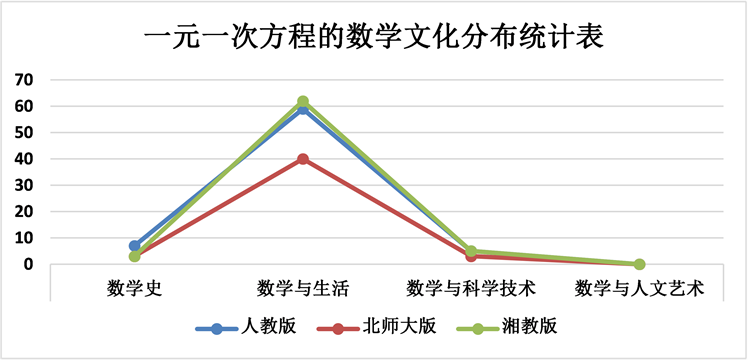
Figure 3. The statistics of mathematical culture distribution of monadic equation
图3. 一元一次方程的数学文化分布统计
在人教版教科书中一元一次方程通过介绍用字母表示数的来源,方程史话和阿尔–花拉子米的《对消与还原》等数学文化;北师大版介绍纸草书、方程小史以及丢番图,湘教版则是比较多的数学与生活问题。人教版和北师大版有部分内容是重合的,即都有扩充相应数学史的丢蕃图。人教版、北师大版和湘教版中的数学史没有重合的部分。在人教版中,最多涉及数学文化的是经济生活问题,其次为日常生活、社会生活,在北师大版中,一元一次方程所涉及的数学文化最多是经济生活类的,学校生活和职业生活最少;在湘教版中,社会生活中渗透数学文化是最常见的方式。研究发现在其他数学文化得到运用水平中,北师大版在文化渗透方面是最高的,而湘教版中数学文化是最低的。数学文化的年级分布呈现“低多高少”的减少趋势,三版教材中的数学文化的数量在各年级要求,但是都呈现出随着年级的提高,数学文化数量减少的趋势,但是减少的幅度有所不同。也就是说,低年级的数学文化数量高于高年级的数学文化数量。
此外,在人教版教材中我们可以看到,小贴士和古代问题,特别是关于“方程史话”阅读材料,对方程的历史进行了系统的介绍,学生可了解通过阅读“方程史话”感受数学思想的历史渊源。但是在这个内容在湘教版中几乎不曾涉及历史,湘教版中唯一一次提到过一个古代数学问题,但是没有涉及到思想方法,通过湘教版中这个“一元一次方程模型及算法”标题可以看出湘教版更注重方程的应用。方程思想对我国数学发展可谓是极其重要,方程中蕴含的解题方法以及算法思想十分丰富,我认为教科书中应当重视介绍方程的历史。
4. 我国传统数学文化融入教科书的途径
教材是教学的蓝本,我们应该先了解数学文化在教材中的呈现情况,立足于教材,根据学生的思维水平和生活经验,提出切合实际的策略。从数学史、应用、思想方法和精神的融入方面进行分析教学,给出以下具体的教学策略。
4.1. 将数学史融入课堂教学
中国古代的数学成就涵盖得非常广,我国古代数学家华蘅提供了22种证明勾股定理的方法,但是教材上并不会展示这些证明方法,因此,教师要拥有丰富的数学史相关知识,知道数学知识点的来龙去脉,为了更好地进行数学课堂教学,我们要善于挖掘数学知识背后的数学文化,启迪学生的发散思维。
在《测圆海镜》的选题中,李冶给出全新的解题方法,他这种一题多解、举一反三的教育思想对于学生得发散思维是大有裨益的,直接让学生体会到天元术思维方法,冲破当时的社会思想束缚,展现了数学先进性和科学性的应用前景,他通过讲学弘扬和普及了“因材施教”、“举一反三”等先进的教育思想和理念 [4]。
4.2. 将数学思想方法融入课堂教学
数学思想方法是在数学概念的形成、问题的解决和知识的应用中逐渐形成和发展起来的,是一种发现式的方式方法和探究式的解题策略。
归纳、演绎、类比等思想蕴含在数学知识的探索应用过程中,通过仔细阅读材料发现教材中数学思想方法的呈现可分为显性和隐性两种形式。显性形式主要是通过阅读直接获得的数学思想方法;隐性形式,主要蕴含在教学内容中,比如体现数形结合的思想有“二次函数的解析式和图像”、“图形面积与乘法公式”、“勾股定理与平方根”等 [5]。
数学模型的思想、统计的思想以及归纳猜想的思想方法等贯穿数学教材的始终。另外,教材中的习题也为数学活动提供了载体,为学生学习运用数学思想提供了空间。
4.3. 将数学美融入课堂教学
从数学语言上来看,数学教科书中具有简洁性、严密性和严谨性。在数学美学层面上,数学的图形与对称、旋转、投影等,体现了数学的对称美、和谐美。另外,数学的广泛性在图形与二次根式,图形与相似,黄金分割点等得到重要体现。
勾股定理形式上的统一简洁美等,数学之美需要学生用心去发现去体会。教科书中几何板块的数学史料仍是稀少,不过在生产生活与人文艺术上呈现较多。数学文化的呈现上,多以生活中的建筑、物体以及事物的特性,抽象出基本的数学图形,探讨概括和研究这些图形的基本特性,让学生体验无处不在的数学。由此可见,空间与图形板块,教科书呈现的数学文化内容较多,有利于数学实验的教学。关于数学图形诸多定理的由来、历史的作用、以及当时数学家不懈探索的历程和数学精神故事也几乎没有在教科书上展示,所以,教师应根据教学需要将这些数学文化融入到数学课堂教学中,扩宽学生的学习视野,陶冶学生的数学情操。
4.4. 将数学精神融入课堂教学
求真意识、反思意识和审美意识等数学精神是数学学习中主要表现形式。数学教材通过数学活动、观察与思考、操作与实践、数学实验等栏目为学生提供空间,让学生通过探索与思考,发现真理,培养数学精神。
数学家们发现新真理、坚持证明、推广的求真意识是数学精神的精华。体现了数学家们的求真意识有勾股定理的证明、无理数的出现等,可见数学精神蕴含于数学知识体系的发展过程中,这需要教师在数学活动中引导学生去感悟和体会数学精神。
总之,教师在日常数学课堂教学中渗透数学史、思想方法、精神和数学美成为教学常态,不可一蹴而就。学校可开展以数学文化为主题的探究活动,让教师和学生在课外时间感受数学的应用和美学价值。
基金项目
基金资助:2020年湖南省普通高等学校教学改革研究项目(HNJG-2020-0492)。