衍射光栅教学中两种计算方法的比较

Comparison of Two Calculation Methods in Diffraction Grating Teaching

摘要: 光栅是波动光学的教学重点之一。对于衍射光栅，我们通常采用波矢法进行讲解，该方法具有易于计算和便于理解的优点，但是适用范围较窄，仅限于黑白光栅。相比而言，复数积分法讲解较少，该方法虽然适用范围广泛，但是不易于学生理解。本文主要比较这两种方法的特点，以及提出利用耦合模理论和傅里叶级数展开的办法来克服复数积分法在在教学中的缺点。

Abstract: Grating is one of the teaching emphases of wave optics. For diffraction gratings, we usually use the wave vector method to explain. This method is easy to calculate and understand, but its scope of application is narrow, and it is limited to black and white gratings. In contrast, the complex integral method is seldom explained. Although it is widely applicable, it is not easy for students to understand. This paper mainly compares the characteristics of these two methods, and proposes the method of using coupled mode theory and Fourier series expansion to overcome the shortcomings of complex integral method in teaching.

1. 引言

光栅是大学物理光学教学中的重要内容，又分为衍射光栅和布拉格光栅两种。其中衍射光栅是介质折射率沿与垂直光传播方向周期性排布的一种无源光学器件，如图1所示，可用在光谱仪、单色仪上 [1] [2]。光栅衍射实际上是由光的相干叠加导致的，在波动光学的教学中，教师最常使用的方法是波矢法，即利用矢量来表示光的电场强度，其中两个矢量的夹角表示其对应的相位差。但是波矢法具有比较大的局限性，它只适用于黑白光栅。除了波矢法外，复数积分法也常用于教学中，它具有适用范围广泛的优点，但是不便于学生理解衍射的物理本质。在本文中，我们首先介绍了波矢法和复数积分法，然后我们对比了两种方法在教学中的优缺点，以及产生这些优缺点的原因。最后，我们提出了在复数积分法的基础上引入耦合模理论以及傅里叶级数展开的方法，使得复数积分法更便于学生理解，提高教学效率 [3]。

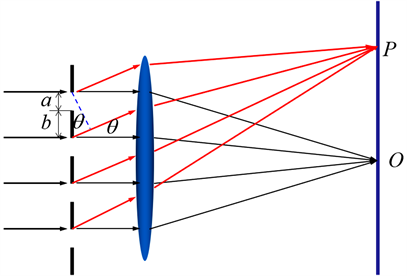
Figure 1. Schematic diagram of one-dimensional diffraction grating

图1. 一维衍射光栅示意图

2. 波矢法和复数积分法

光栅衍射分为近场的菲涅尔衍射和远场的夫琅禾费衍射，无论是物理专业学生的光学课程，还是非物理专业学生的大学物理课程，都主要介绍夫琅禾费衍射，如图1所示，本文也主要讨论夫琅禾费衍射。在大多数教师的衍射教学中，通常介绍两种方法，分别为波矢法何复数积分法，物理使用何种方法，光栅的衍射图样都满足关系

衍射图样 = 单缝衍射因子 × 缝间干涉因子 (1)

其中单缝衍射因子可以通过波矢法和复数积分法分别计算，而缝间干涉因子则只采用光差法计算最为方便，下面我们先分别简单介绍不同因子的原理。

2.1. 波矢法计算单缝衍射因子

首先我们考虑如图2(1)所示的狭缝，当一束平行光照射在该狭缝AB上时，在光屏上会产生衍射图样，该衍射图样具有中间条纹最粗，两侧条纹等间隔粗细的特点，也就是沿着不同衍射方向 $\theta$，光的强度不同，人们把这种现象称为单缝衍射。而波矢法则是利用微积分的思想，结合几何性质推导单缝衍射光强的计算公式 [3]。以图2(1)为例，沿 $\theta$ 方向，在与衍射方向垂直的等相位面上，从A点衍射的光线比从B点衍射的光线产生一个光程差

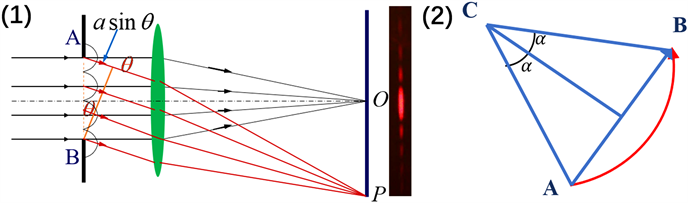
Figure 2. Schematic diagram of single slit diffraction factor calculated by wave vector method

图2. 波矢法计算单缝衍射因子示意图

$\delta =a\sin \theta$ (2)

其中a为狭缝的宽度，而该光程差所对应的相位差为

$2\alpha =\frac{2\pi }{\lambda }a\sin \theta =ka\sin \theta$ (3)

其中 $\lambda$ 是光的波长。从该公式中，我们可以看到当光线之间存在光程差时，也对应于一个相位差，即波矢的角度差。现在利用微积分思想，我们将a划成N个相等的间隔长度，那么在每个间隔内都可以用一个波矢量来表示，并且相邻的波矢量之间有相同的夹角。现在我们让这些波矢首尾依次相连，当 $N\to \infty$ 时，我们会发现这些波矢将会成一个弧形，如图2(2)中红色弧线所示。此时，这些波矢的叠加就构成了衍射光在该方向上的总的矢量，即 $A_{\theta }=AB$。根据几何关系，显然可知 $AB$ 所对应的圆心角为 $2\alpha$。接下来，我们需要确认 $AB$ 的长度，根据几何关系可知

$\{\begin{array}{l}\stackrel{⌢}{AB}=2\alpha R\\ \overline{AB}=2\sin \alpha R\end{array}$ (4)

下面，我们来看一下 $\stackrel{⌢}{AB}$ 所对应的物理含义，它实际上等于上文中讨论的每个等间隔划分所对应的波矢依次沿直线叠加，这也就是说每个波矢之间的夹角恒等于0，而这种情形仅在 $\theta =0$ 时成立，所以我们可以设在光屏中央处的光线的电场强度大小为 $A_0$，则有 $A_0\propto \stackrel{⌢}{AB}$，那么结合该结果和(4)式，我们可以得到

$A_{\theta }=A_0\frac{\sin \alpha }{\alpha }$ (5)

该关系即为沿 $\theta$ 方向光线振幅的关系表达式，进而得到光强的关系即为

$I_{\theta }=I_0{\left|\frac{\sin \alpha }{\alpha }\right|}^2$ (6)

2.2. 复数积分法计算单缝衍射因子

除了波矢方法外，学生还可以根据光在均匀介质中传播的特点，对单缝衍射因子进行计算。那么依据的公式就是菲涅尔–基尔霍夫公式 [4]。由于我们讨论的是夫琅禾费衍射，因此该公式的前提条件天然满足。当光垂直射向光栅时，光栅在横向方向折射率成周期分布，但是纵向方向折射率保持不变。因此可以直接写出透射函数

$T\left(x\right)={\text{e}}^{ikLn\left(x\right)}$ (7)

其中L是光栅在纵向方向的厚度，光的波矢 $k=2\pi /\lambda$， $\lambda$ 为入射光的波长， $n\left(x\right)$ 是光栅在x位置的折射率。那么(7)式仅为透射光在实空间中的分布，而对于夫琅禾费衍射，需要考虑透射光在远场不同角度的分布，因此，我们还需要对(7)式进行傅里叶变换，使其从实空间变换到角空间中。当然，我们并不是直接变换到角空间中，而是需要经过换算。换算过程如下，与位置x关于傅里叶变换对应的物理量是动量k，而由于光在衍射后，会偏离原来的传播方向，所以k的方向不再沿垂直光栅的方向，而是有横向的分量 $k\sin \theta$。因此我们可以把这个横向的分量和x做傅里叶变换关系。因此有

$A\left(\theta \right)={\displaystyle {\int }_{-d/2}^{d/2}T\left(x\right){\text{e}}^{-ikx\sin \theta }\text{d}x}$ (8)

由于我们考虑的是夫琅禾费衍射，因此透射光的角度谱在衍射后不再发生改变。

2.3. 缝间干涉因子

对于波矢法和复数积分法，缝间干涉因子的计算方法是相同的，均采用波矢法。参照2.1节的内容，我们可很容易理解缝间因子的计算。如图3当计算缝间干涉因子时，我们就不用再对整个光栅进行无穷多组分的划分了，而是直接将每个周期后的透射的光用一个波矢 $A_i$ 来表示，那么这些波矢的叠加就是缝间干涉后的最终效果，那么每个波矢之间的夹角是多大呢？由于两个相邻的周期间隔为光栅常数d，那么就可以得到相邻的两个波矢之间的夹角应为 $2\beta =kd\sin \theta$。根据几何关系，我们可得缝间干涉因子为

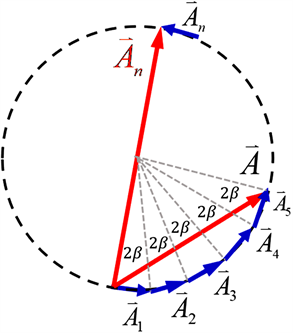
Figure 3. Schematic diagram of inter seam interference factor calculation

图3. 缝间干涉因子计算示意图

$\left|\frac{A}{A_i}\right|=\frac{\sin N\beta }{\sin \beta }$ (9)

3. 两种方法的比较

3.1. 波矢法

根据2.1节和2.3节的内容，我们可以得到波矢法对应的光栅衍射公式

$I\left(\theta \right)=I\left(0\right){\left(\frac{\sin \alpha }{\alpha }\right)}^2{\left(\frac{\sin N\beta }{N\sin \beta }\right)}^2$ (10)

该方法的优点是计算过程比较简便，不需要复杂的数值计算，而且在推到过程中可以更加直观向学生展示出来波动光学具有的干涉叠加原理。推导过程中只有波矢的偏夹角 $\alpha$ 和 $\beta$ 的计算稍微具有难度，所以说该方法不仅适合向物理专业学生介绍，也适合于向非物理专业学生介绍。

除此之外，从该方法衍生出来的半波带法，也值得重点讲解。半波带法实际上是波矢法的一个简化版本，它是指将单缝的最大光程差 $a\sin \theta$ 与半波长 $\lambda /2$ 进行比较，当 $N=2a\sin \theta /\lambda$ 为零时，对应于 $\theta =0$，即中间亮条纹。而当N为偶数时，我们可以认为在同一个狭缝中总存在两个相位相差 $\pi$ 的波矢发生相互抵消，从而导致在光屏后面出现相消干涉，产生暗纹，进而导致光栅衍射条纹的缺级现象。半波带法有助于学生们理解暗纹的产生和暗纹特点，尤其适用于快速判断光栅衍射图样。

但是波矢法也存在明显缺点，从推导过程中，我们可以看到波矢法只适用于黑白光栅，而其他类型的光栅则无法适用该公式，而在生产生活中，大量使用的光栅实际上并不是黑白光栅，对学生后续其他课程的学习设置了比较大的障碍。其次，该方法只适用于推导衍射图样对称的光栅，对于非对称光栅无法使用。而非对称衍射光栅实际上越来越受到科学研究的重视。

3.2. 复数积分法

根据2.2节和2.3节的内容，我们可以得到复数积分法对应的光栅衍射公式

$I\left(\theta \right)={\left|A\left(\theta \right)\right|}^2{\left(\frac{\sin N\beta }{N\sin \beta }\right)}^2$ (11)

与波矢方法相比，复数积分法显然具有更广泛的适用范围。无论衍射光栅的每个周期内的折射率如何，我们都可以通过数值计算的办法得到 $A\left(\theta \right)$ 的表达式，进而计算出衍射图样，很好的弥补了波矢法的不足。但是该方法也具有不足，即不能直观的展示波的叠加过程。并且在推导过程中，我们使用了正则物理量之间的傅里叶变换关系，该关系较波矢法中的向量计算，更为抽象，对于学生的理解物理问题增加了难度。

除此之外，该方法更适合物理专业学生或光学相关专业的学生，因为随着现代光学对光栅器件特殊性质的要求，人们希望设计更为特殊的衍射图样，例如非对称衍射光栅。而波矢法只适合衍射图样对称的光栅，而复数积分法则没有相关限制。

为进一步说明，我们以图4为例，假设介质的折射率为 $n\left(x\right)=1+0.5\cos \left(4x\right)+0.2i\cos \left(4x+\phi \right)$，其中光栅厚度 $L=k/4$，光栅常数 $d=4\lambda$，光栅周期数 $N=40$。在图4(a)中，我们令 $\phi =0$，此时光栅的衍射图样为对称图样，并且能量多集中在零和正负一级条纹中，呈现中间高两边低的特点；在图4(b)中，我们 $\phi =0.5\pi$，此时光栅的衍射图样为非对称图样，虽然还是中间的亮度最高，但是左侧一级条纹的亮度已经明显高于右侧的一级条纹。该例可以证明对于特殊衍射情况的光栅，复数积分法可以更好地描述衍射情况。

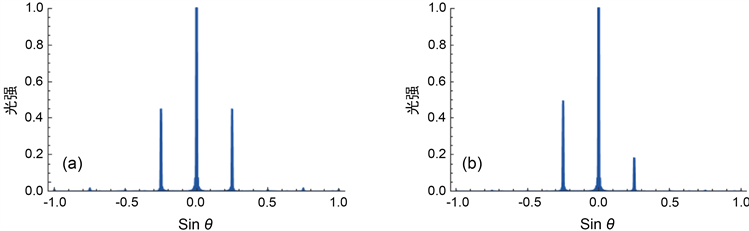
Figure 4. Diffraction pattern calculated by complex integral method

图4. 复数积分法计算的衍射图样

3.3. 复数积分法的扩展

复数积分法的缺点是不方便学生理解，实际上这一缺点是可以被克服的，比如说引入傅里叶光学的相关概念 [5] [6]。根据耦合模理论可知，我们总可以将(7)式进行傅里叶展开，写成如下形式

$T\left(x\right)=T_0+{\displaystyle \underset{n\ne 0}{\sum }{T}_n{\text{e}}^{i2\pi f_{n}x}}$ (12)

其中 $f_n=n/d$ 和

$T_n=\frac{1}{d}{\displaystyle {\int }_{-d/2}^{d/2}T\left(x\right){\text{e}}^{-i2\pi f_{n}x}\text{d}x}$ (13)

结合耦合模理论和(12)式，我们可以看到，任何一级的衍射条纹的强弱和 ${\left|T_n\right|}^2$ 成正比，如果 ${\left|T_n\right|}^2=0$，则说明该条纹为缺级现象，若 ${\left|T_n\right|}^2>{\left|T_m\right|}^2$，则说明第n级条纹的光强高于第m级条纹。这是由于在周期介质中传播的光的振幅也应该是周期的，不同级次的衍射条纹对应于的波矢沿周期方向的分量不同导致的。那么，结合该解释，可以更好地向学生解释为什么会出现不同级次的衍射条纹以及它们数值不同的原因。

4. 结束语

通过介绍分析衍射光栅的衍射图样的计算公式，我们得到了波矢法和复数积分法在教学中的特点。其中波矢法具有简单易懂，凸出光具有相干叠加性的特点，易于学生理解和计算。但是该方法也具有明显的缺点，只可以计算黑白光栅的特殊情形。与之相比，复数积分法则具有方便计算，适用范围广的优点，各种光栅都可以用该公式计算，但是缺失了易于理解的优点，该方法适用的傅里叶变换在大学物理教学中并不是特别易于学生理解。为了克服该缺点，我们认为在物理教学过程中引入耦合模理论可以有效帮助学生理解该方法。

基金项目

2021年度辽宁省普通高等教育本科教学改革研究优质教学资源建设与共享项目：金课视角下基于跨校修读方式的研究性物理实验内容的多元考核探索与实践；2022年辽宁省普通高等教育本科教学改革研究优质教学资源建设与共享项目：在混合式实验教学中开展跨校修读的探索与实践；2022年沈阳航空航天大学理学院教改项目：线上和线下混合式实验教学模式的探索和建设；2022年度辽宁省普通高等教育本科教学改革研究优质教学资源建设与共享项目：基于跨校修读的实践类课程创新教育引导及能力培养；2022年度沈阳航空航天大学校级教改项目：依托国家一流课程，建设物理实验课程实验报告批改及管理系统。