一类具有余弦核的积分差分方程的分析

Analysis of a Class of Integrodifference Equations with Cosine Kernel

摘要: 捕食与被捕食是经典的生态学种间关系，本文首先建立了一类世代重叠的离散时间捕食与被捕食模型并讨论了其不动点的稳定性。物种的空间扩散是普遍存在的，我们加入余弦核函数，建立了一类可以描述两个物种在空间中相互作用的积分差分方程模型，而这种无穷维离散时间空间扩散系统可以在余弦核下简化为有限维系统。我们分析了其与非空间模型对应的不动点稳定性并讨论了引入的空间参数对模型动力学的影响。最后通过数值分析验证了主要结论。

Abstract: Predation-prey are classical ecological interspecific relationships. In this paper, we first establish a class of discrete-time predation-prey models with overlapping generations and discuss the stability of their fixed points. The spatial diffusion of species is universal, and we incorporate cosine kernel functions to establish a class of integrodifference equations that can describe the interaction of two species in space, and this infinite-dimensional discrete-time spatial diffusion system can be reduced to a finite-dimensional system under the cosine kernel. We analyze its fixed point stability corre-sponding to the non-spatial model and discuss the effect of the introduced spatial parameters on the model dynamics. Finally, the main conclusions are verified by numerical analysis.

1. 引言

捕食、竞争、共生、寄生是自然界常见的生物关系，其中捕食关系是最普遍也最重要的种间关系之一，研究捕食关系无论是对自然还是对人类，都有着十分深远的意义。早在1923年Lotka [1] 和Volterra [2] 就分别提出经典的捕食与被捕食微分方程模型，统称为Lotka-Volterra系统。随后，捕食与被捕食模型得到各方面的改进和发展 [3] - [12]，为生态学研究提供了丰富的材料。另外，由于对野外种群的观测数据是离散的，建立离散时间模型来研究捕食与被捕食种群数量的演化是一个合理的选择。

扩散是自然界一种普遍存在的客观现象，任何生物或多或少都存在扩散行为。在许多描述扩散现象的模型中，积分差分方程是一个相对较新的概念。这是一类时间离散空间连续的无穷维动力系统，常用于描述在一个生命周期内增长和扩散分离的物种的数量变化。这类物种的增长通常是季节性的，所以离散的时间是非常有意义的，而扩散阶段的情况通常较为复杂，用扩散核来表示，则更加具有现实意义 [13]。1982年Weinberger [14] 首次给出了积分差分方程的递归形式，1986年Kot和Schaffer [15] 在研究世代不重叠单种群扩散现象时导出了积分差分模型：

$N_{t+1}\left(x\right)={\displaystyle {\int }_{\Omega }K}\left(x,y\right)F\left(N_t\left(y\right)\right)\text{d}y.$

$N_t\left(x\right)$ 表示t时刻物种在一维有界栖息地 $\Omega$ 的种群密度。该模型用满足 $F\left(0\right)=0$， $N>0$ 时 $F\left(N\right)>0$ 的增长函数F来描述物种的增长阶段，用从初始位置y扩散到其他位置的概率密度函数 $K\left(x,y\right)$ 来描述物种的扩散阶段，由于扩散核是概率密度函数，对于所有的 $y\in \Omega$，扩散核一定满足 ${\displaystyle {\int }_{\Omega }K}\left(x,y\right)\text{d}y\le 1$。同时，

扩散核的选取具有多样性，最常用的扩散核是高斯核 [16] 和拉普拉斯核 [17]，除此之外还有可分离核，写作

$K\left(x,y\right)={\displaystyle \underset{j=1}{\overset{m}{\sum }}{K}_1^{\left(j\right)}}\left(x\right)K_2^{\left(j\right)}\left(y\right).$

1986年kot和Schaffer [15] 发现当扩散核可分时，无限维的积分差分方程可简化为有限维差分方程组。

他们取增长函数为logistic函数 $F\left(N\right)=\left(r+1\right)N-r{N}^2$，扩散核函数为余弦核，空间域为长度为L的一维有界同质区域 $\Omega$，假设 $N_t\left(x\right)=a_t\cos \left(\frac{\pi x}{2R}\right)+b_t\sin \left(\frac{\pi y}{2R}\right)$ 并代入积分差分方程中，通过计算得到简化的二

维差分方程组：

$\{\begin{array}{l}{a}_{t+1}=\left(c_1-c_2{a}_t\right)a_t-c_3{b}_t^2,\hfill \\ b_{t+1}=\left(c_4-c_5{a}_t\right)b_t.\hfill \end{array}$ (1)

其中 $c_1\text{-}{c}_5$ 是关于 $L,R,r$ 的多项式。根据(1)的表达式Kot和Schaffer发现 $\left\{b_t=0\right\}$ 是此系统的不变流形， $-1<c_4-c_5{a}_t<1$ 时，不变流形 $\left\{b_t=0\right\}$ 是吸引的，在该不变流形上 $a_t$ 的方程与logistic方程形式相同。2019年Bramburger和Lutscher [18] 给出了模型(1)不变流形 $\left\{b_t=0\right\}$ 局部吸引的详细证明，说明了在一定条件下具有logistic增长函数的积分差分方程可以展示logistic模型的全部动力学行为。他们还指出，由于积分差分方程的分析比较困难，这种简化的、特殊的、显式可解的情况十分重要，最后他们将此种方法应用到一个竞争模型和一个捕食模型当中。

本文的第一部分首先建立了一个世代重叠、时间离散的捕食与被捕食模型，研究了这个模型不动点的稳定性。第二部分再选取余弦核函数作为扩散核，建立了一个积分差分方程组，利用可分离核性质将其简化为有限维差分方程组，研究了其与非空间模型对应的不动点的稳定性，同时探究引入空间扩散因素对模型动力学行为的影响，得到主要结论：考虑空间因素在不变流形上的某些参数平面不改变对应不动点的定性性质。第三部分利用数值模拟验证了主要结论。

2. 非空间模型

2.1. 模型的建立

1992年Neubert和Kot [12] 研究了当被捕食者符合logistic增长时捕食与被捕食模型的三个不动点的稳定性，以及不动点失去稳定性时的分支情况，模型如下：

$\{\begin{array}{l}{N}_{t+1}=r{N}_t\left(1-N_t-P_t\right),\hfill \\ P_{t+1}=s{N}_t{P}_t.\hfill \end{array}$ (2)

其中 $N_t,P_t$ 分别代表第t代或在t时刻被捕食者与捕食者的种群密度，r指被捕食者的增长参数，被捕食者 $N_t$ 符合logistic增长。该模型在第一象限不能保持正性，可能出现负的种群数量，但比起其他模型，此类模型更容易分析。若考虑t为时刻，假设t时刻到 $t+1$ 时刻之间捕食者的死亡率为 $d<1$，则捕食者的幸存率为 $1-d$，再考虑捕食者受到密度制约，建立模型如下：

$\{\begin{array}{l}{N}_{t+1}=r{N}_t\left(1-N_t-P_t\right),\hfill \\ P_{t+1}=s{N}_t{P}_t+\left(1-d\right)P_t-\delta P_t^2.\hfill \end{array}$ (3)

其中 $N_t,P_t$ 分别表示被捕食者与捕食者在t时刻的种群密度，r表示被捕食者的增长系数，s表示捕食者捕食猎物后的转化率，d表示捕食者的死亡率， $\delta$ 表示捕食者的种内竞争系数，模型中的参数全部为正。与模型(2)相似，模型(3)在第一象限不能保持正性，但若种群密度为正， $r,s$ 一定满足 $r\in \left(0,4\right),s\in \left(0,3+d\right)$，以下我们只在 $r\in \left(0,4\right),s\in \left(0,3+d\right)$ 范围内讨论。

2.2. 模型分析

通过计算下面的方程组

$\{\begin{array}{l}n=rn\left(1-n-p\right),\hfill \\ p=snp+\left(1-d\right)p-\delta p^2.\hfill \end{array}$ (4)

得到模型(3)的三个不动点分别是： $\left(0,0\right)$， $\left(\frac{r-1}{r},0\right)$， $\left(\frac{\delta \left(r-1\right)+dr}{r\left(\delta +s\right)},\frac{s\left(r-1\right)-dr}{r\left(\delta +s\right)}\right)$。它们分别表示：

捕食者与被捕食者同时灭绝的状态、被捕食者持久而捕食者灭绝的状态和二者共存的状态。要保证不动

点在第一象限内，同时满足 $r\in \left(0,4\right),s\in \left(0,3+d\right)$，简单计算可得边界平衡点 $\left(\frac{r-1}{r},0\right)$ 的存在条件为 $1<r<4$， 正平衡点 $\left(\frac{\delta \left(r-1\right)+dr}{r\left(\delta +s\right)},\frac{s\left(r-1\right)-dr}{r\left(\delta +s\right)}\right)$ 的存在条件为 $\frac{dr}{r-1}<s<3+d$。

下面我们讨论各个不动点的稳定性。

定理2.1 对于模型(2)不动点的稳定性，有以下结论

1) 若 $r\in \left(0,1\right)$，则平凡不动点 $\left(0,0\right)$ 局部渐近稳定。

2) 若 $r\in \left(1,\frac{3+d}{3}\right),s<3+d$ 或 $r\in \left(\frac{3+d}{3},3\right),s<\frac{dr}{r-1}$，则边界不动点 $\left(\frac{r-1}{r},0\right)$ 局部渐近稳定。

3) 满足以下任意一个条件，正不动点 $\left(\frac{\delta \left(r-1\right)+dr}{r\left(\delta +s\right)},\frac{s\left(r-1\right)-dr}{r\left(\delta +s\right)}\right)$ 是局部渐近稳定的：

a) $\frac{3+d}{3}<r<\frac{3+d}{2},\frac{dr}{r-1}<s<3+d.$

b) $\frac{3+d}{2}<r<3,\frac{dr}{r-1}<s<\frac{dr+r}{r-1}.$

c) $\frac{3+d}{2}<r<3,\frac{dr+r}{r-1}<s<3+d,\delta >\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)}.$

d) $3<r<4,\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}<s<\frac{dr+r}{r-1},\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}.$

e) $3<r<2+\frac{d+\sqrt{16+d^2}}{4},\frac{dr+r}{r-1}<s<3+d,$ $\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)}<\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}.$

f) $2+\frac{d+\sqrt{16+d^2}}{4}<r<4,\frac{dr+r}{r-1}<s<\frac{dr\left(r-2\right)+r\left(r-1\right)}{\left(r-2\right)\left(r-1\right)},$ $\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)}<\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}.$

4) $r=1$ 时，平凡不动点 $\left(0,0\right)$ 可能发生跨临界分支； $r=3$ 时，边界不动点 $\left(\frac{r-1}{r},0\right)$ 发生倍周期分支； $s=\frac{dr}{r-1}$ 时，边界不动点 $\left(\frac{r-1}{r},0\right)$ 可能发生跨临界分支； $\delta =0,s=\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}$ 时，正不动点发生倍周期分支； $\delta =0,s=\frac{dr+r}{r-1}$ 时，则正不动点发生Neimark-Sacker分支。

可给出模型不动点稳定性的分布图1：区域①中平凡不动点 $\left(0,0\right)$ 局部渐近稳定，区域②中边界不动点 $\left(\frac{r-1}{r},0\right)$ 局部渐近稳定，区域③中正不动点局部渐近稳定，区域④~⑥为正不动点局部渐近稳定时，捕

食者出生率s和被捕食者出生率r满足的范围(当 $s,r$ 在此区间内还要保证 $\delta$ 也在一定范围内，才有正不动点局部渐近稳定和分支的出现)，T：跨临界分支，PD：倍周期分支，NS：Neimark-Sacker分支。下面给出定理2.1的证明。

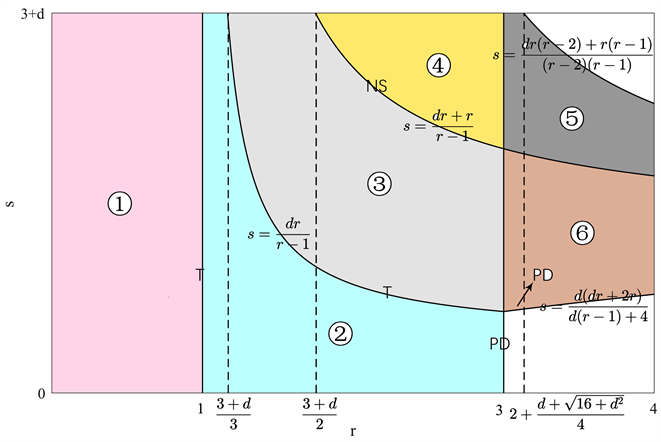
Figure 1. Stable interval distribution of immobile points

图1. 不动点稳定区间分布

证明：模型(3)的Jacobi矩阵为：

$J_1=\left(\begin{array}{cc}r\left(1-n-p\right)-rn& -rn\\ sp& sn+1-d-2\delta p\end{array}\right).$

首先证明平凡不动点 $\left(0,0\right)$ 的稳定性，在 $\left(0,0\right)$ 处的Jacobi矩阵为

$J_{\left(0,0\right)}=\left(\begin{array}{cc}r& 0\\ 0& 1-d\end{array}\right).$

$J_{\left(0,0\right)}$ 为二阶对角矩阵，特征值 ${\lambda }_1=r,{\lambda }_2=1-d$，不动点 $\left(0,0\right)$ 局部渐近稳定需要满足： $\left|{\lambda }_1\right|,\left|{\lambda }_2\right|<1$ [19]，由于 $0<1-d<1$ 恒成立，只需满足 $0<r<1$。即 $0<r<1$ 时不动点 $\left(0,0\right)$ 局部渐近稳定。在 $r=1$ 时，特征值满足 $\left|{\lambda }_1\right|=1$ 且 $\left|{\lambda }_2\right|<1$，模型在不动点 $\left(0,0\right)$ 处可能发生跨临界分支 [20]，但具体的分支类型和分支稳定

性本文暂时不做讨论。

再证明边界不动点 $\left(\frac{r-1}{r},0\right)$ 的局部稳定性，当 $1<r<4$ 时， $\left(\frac{r-1}{r},0\right)$ 处的Jacobi矩阵为

$J_{\left(\frac{r-1}{r},0\right)}=\left(\begin{array}{cc}2-r& 1-r\\ 0& \frac{s\left(r-1\right)}{r}+1-d\end{array}\right).$

$J_{\left(\frac{r-1}{r},0\right)}$ 是一个上三角矩阵，特征值 ${\lambda }_1=2-r$， ${\lambda }_2=\frac{s\left(r-1\right)}{r}+1-d$，通过计算不等式 $\left|2-r\right|,\left|\frac{s\left(r-1\right)}{r}+1-d\right|<1$，可得 $1<r<\frac{3+d}{3},s<3+d$ 或 $\frac{3+d}{3}<r<3,s<\frac{dr}{r-1}$ 时，边界不动点 $\left(\frac{r-1}{r},0\right)$ 局部渐近稳定。通过计算 $\left|2-r\right|,\left|\frac{s\left(r-1\right)}{r}+1-d\right|=1$，得到模型的分支情况： $r=3,s<\frac{dr}{r-1}$ 时，特征值满足 ${\lambda }_1=-1$ 且 $\left|{\lambda }_2\right|<1$，此时在不动点 $\left(\frac{r-1}{r},0\right)$ 处发生倍周期分支， $s=\frac{dr}{r-1}$ 且 $1<r<3$ 时，特征值满足 $\left|{\lambda }_1\right|<1$ 且 ${\lambda }_2=1$，此时模型在不动点 $\left(\frac{r-1}{r},0\right)$ 处可能发生跨临界分支。

最后证明正不动点 $\left(\frac{\delta \left(r-1\right)+dr}{r\left(\delta +s\right)},\frac{s\left(r-1\right)-dr}{r\left(\delta +s\right)}\right)$ 的局部稳定性，满足 $\frac{dr}{r-1}<s<3+d$ 时，将正不动点记作 $\left(n^{*},p^{*}\right)$ 代入 $J_1$，得到该点处的Jacobi矩阵为

$J_{\left(n^{*},p^{*}\right)}=\left(\begin{array}{cc}1-r{n}^{*}& -r{n}^{*}\\ s{p}^{*}& 1-\delta p^{*}\end{array}\right),$

其特征方程为

$F\left(\lambda \right)={\lambda }^2-\left(1-r{n}^{*}+1-\delta p^{*}\right)\lambda +1-r{n}^{*}-\delta p^{*}+r\left(s+\delta \right)n^{*}{p}^{*}.$ (5)

根据Jury判据，当特征方程满足 $F\left(1\right)>0,F\left(-1\right)>0,F\left(0\right)<1$ 时， $\left|{\lambda }_1\right|,\left|{\lambda }_2\right|<1$，正不动点局部渐近稳定 [20]。

首先讨论满足 $F\left(1\right)>0$ 时的情况，将 $\lambda =1$ 带入特征方程(5)有

$F\left(1\right)=\frac{\left[\delta \left(r-1\right)+dr\right]\left[s\left(r-1\right)-dr\right]}{r\left(s+\delta \right)},$

在 $1+\frac{d}{3}<r<4,\frac{dr}{r-1}<s<3+d$ 条件下， $F\left(1\right)>0$ 恒成立。

再讨论满足 $F\left(-1\right)>0$ 时的情况，将 $\lambda =-1$ 带入特征方程(5)有

$\begin{array}{c}F\left(-1\right)=4-2r{n}^{*}-2\delta p^{*}+r(\delta +s)n^{*}{p}^{*}\\ =\frac{4r\left(\delta +s\right)-2r\left[\delta \left(r-1\right)+dr\right]-2\delta \left[s\left(r-1\right)-dr\right]+\left[\delta \left(r-1\right)+dr\right]\left[s\left(r-1\right)-dr\right]}{r\left(\delta +s\right)}\\ =\frac{\delta \left(r-3\right)\left[s\left(r-1\right)-dr-2r\right]+dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{r\left(\delta +s\right)}\\ =\frac{\left[\delta \left(r-3\right)+dr\right]\left[s\left(r-1\right)-dr-2r\right]+4sr}{r\left(\delta +s\right)},\end{array}$

要保证 $F\left(-1\right)>0$，有 $\left[\delta \left(r-3\right)+dr\right]\left[s\left(r-1\right)-dr-2r\right]+4sr>0$ 即可。与参考文献 [18] 不同，这里在模型中增加了两个参数 $\delta ,d$，使得稳定区间的划分、分支的存在条件都更为复杂。

下面进行分类讨论：

$s>\frac{dr+2r}{r-1}$ 时， $s\left(r-1\right)-dr-2r>0$，通过计算可知 $s=\frac{dr+2r}{r-1}$ 由 $r=1$ 处从正无穷递减在 $r=3+d$ 处与 $s=3+d$ 相交，故 $\frac{dr+2r}{r-1}<s<3+d$ 只有在 $r>3+d$ 时才成立，此时 $r-3>0$，显然有 $\left[\delta \left(r-3\right)+dr\right]\left[s\left(r-1\right)-dr-2r\right]+4sr>0$。

$s<\frac{dr+2r}{r-1}$ 时， $s\left(r-1\right)-dr-2r<0$，在此条件下有两种情况：

若满足 $\delta \left(r-3\right)+dr<0$，一定有 $\left[\delta \left(r-3\right)+dr\right]\left[s\left(r-1\right)-dr-2r\right]+4sr>0$。根据前面的计算 $s=\frac{dr+2r}{r-1}$ 与 $s=3+d$ 在 $r=3+d$ 处相交，那么 $s<\frac{dr+2r}{r-1}$ 同时满足 $s<3+d$ 时， $s,r$ 的取值范围为： $1<r<3+d$ 时， $s<3+d$ ； $3+d<r<4$ 时， $s<\frac{dr+2r}{r-1}$。但 $\delta \left(r-3\right)+dr<0$ 只在 $1<r<3$ 时可取到，即 $1<r<3$， $\frac{dr}{r-1}<s<3+d$， $\delta >\frac{dr}{3-r}$ 时 $F\left(-1\right)>0$。

若满足 $\delta \left(r-3\right)+dr>0$ 又会有更复杂的情况，继续进行分类讨论：

$r>3$ 时， $\delta \left(r-3\right)+dr>0$ 恒成立，此时无法通过多项式各项的正负直接判断，还需进一步计算

$\left[\delta \left(r-3\right)+dr\right]\left[s\left(r-1\right)-dr-2r\right]>-4sr,$

通过计算可知，在此条件下，若 $\delta$ 满足 $\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}$，就有 $F\left(-1\right)>0$。由于参数 $\delta >0$，这里要保证 $dr\left[s\left(r-1\right)-dr-2r\right]+4sr>0$，即s满足 $s>\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}$。那么 $r>3$ 时， $s,\delta$ 满足 $\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}<s<\frac{dr+2r}{r-1}$， $\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}$ 时有 $F\left(-1\right)>0$。

$1<r<3$ 时，若 $\delta <\frac{dr}{3-r}$， $\delta \left(r-3\right)+dr>0$，再满足 $\delta >\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}$，有 $F\left(-1\right)>0$。 通过计算可知， $s=\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}$ 与 $s=\frac{dr}{r-1}$ 在 $r=3$ 处相交， $1<r<3$ 时， $\frac{dr}{r-1}>\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}$，那么在 $s>\frac{dr}{r-1}$ 的条件下， $dr\left[s\left(r-1\right)-dr-2r\right]+4sr$ 的值一定为正，此时 $\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}<0$，由于参数 $\delta$ 恒为正，只要取 $\delta >0$ 即可，即 $1<r<3$， $\frac{dr}{r-1}<s<3+d$， $0<\delta <\frac{dr}{3-r}$ 时有 $F\left(-1\right)>0$。

综上， $F\left(-1\right)>0$ 当且仅当 $r,s,\delta$ 满足以下任意条件：

a) $r>3+d,\frac{dr+2r}{r-1}<s<3+d.$

b) $3<r<3+d,\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}<s<3+d,\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}.$

c) $3+d<r<4,\frac{d\left(dr+2r\right)}{d\left(r-1\right)+4}<s<\frac{dr+2r}{r-1},\delta <\frac{dr\left[s\left(r-1\right)-dr-2r\right]+4sr}{\left(3-r\right)\left[s\left(r-1\right)-dr-2r\right]}.$

d) $1+\frac{d}{3}<r<3,\frac{dr}{r-1}<s<3+d.$

$F\left(-1\right)>0$ 的情况讨论完毕。

最后讨论满足 $F\left(0\right)<1$ 时的情况，将 $\lambda =0$ 带入特征方程(5)有

$\begin{array}{c}F\left(0\right)=1-r{n}^{*}-\delta p^{*}+r\left(\delta +s\right)n^{*}{p}^{*}\\ =1+\frac{-r\left[\delta \left(r-1\right)+dr\right]-\delta \left[s\left(r-1\right)-dr\right]+\left[\delta \left(r-1\right)+dr\right]\left[s\left(r-1\right)-dr\right]}{r\left(\delta +s\right)},\end{array}$

要保证 $F\left(0\right)<1$，即 $\frac{-r\left[\delta \left(r-1\right)+dr\right]-\delta \left[s\left(r-1\right)-dr\right]+\left[\delta \left(r-1\right)+dr\right]\left[s\left(r-1\right)-dr\right]}{r\left(\delta +s\right)}<0$，由于 $r\left(\delta +s\right)>0$， $F\left(0\right)<1$ 等价于

$-r\left[\delta \left(r-1\right)+dr\right]-\delta \left[s\left(r-1\right)-dr\right]+\left[\delta \left(r-1\right)+dr\right]\left[s\left(r-1\right)-dr\right]<0,$

化简后为

$\left[s\left(r-1\right)-dr-r\right]\left[\delta \left(r-1\right)+dr\right]-\delta \left[s\left(r-1\right)-dr\right]<0,$

其中 $\delta \left(r-1\right)+dr,\left(r-1\right)-dr>0$ 在 $1+\frac{d}{3}<r<4,\frac{dr}{r-1}<s<3+d$ 时恒成立。

下面进行分类讨论：

$s\left(r-1\right)-dr-r<0$，即 $s<\frac{dr+r}{r-1}$ 时，通过各式的正负性，直接可以判断有 $F\left(0\right)<1$。但还需保证 $s<3+d$，通过计算可知， $s=\frac{dr+r}{r-1}$ 由 $r=1$ 从正无穷递减与 $s=3+d$ 在 $r=\frac{3+d}{2}$ 处相交，即 $r,s$ 满足 $1<r<\frac{3+d}{2},s<3+d$ ； $\frac{3+d}{2}<r<4,s<\frac{dr+r}{r-1}$ 时 $F\left(0\right)<1$。

$s\left(r-1\right)-dr-r>0$，即 $\frac{3+d}{2}<r<4$， $\frac{dr+r}{r-1}<s<3+d$ 时，这种情况下不能直接判断，我们还需要讨论 $\delta$ 的情况，换一种因式分解方式得到：

$\delta \left\{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)\right\}+dr\left[s\left(r-1\right)-dr-r\right]<0.$

下面再进行分类讨论：

$\frac{3+d}{2}<r<2$， $\delta \left\{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)\right\}<0$，若 $\delta >\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)}$ 有 $F\left(0\right)<1$。

$2<r<4$，且 $s<\frac{dr\left(r-2\right)+r\left(r-1\right)}{\left(r-2\right)\left(r-1\right)}$ 时， $\delta \left\{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)\right\}<0$，若 $\delta$ 满足 $\delta >\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)}$，有 $F\left(0\right)<1$。

通过计算可知， $2<r<4$ 时， $s=\frac{dr\left(r-2\right)+r\left(r-1\right)}{\left(r-2\right)\left(r-1\right)}$ 从 $r=2$ 处由无穷递减并与 $s=3+d$ 相交， $r>2$ 时，这两条曲线在 $r=2+\frac{d+\sqrt{16+d^2}}{4}$ 处相交，于是 $s<\frac{dr\left(r-2\right)+r\left(r-1\right)}{\left(r-2\right)\left(r-1\right)}$ 同时满足 $s<3+d$ 时， $s,r$ 的取值范围为： $2<r<2+\frac{d+\sqrt{16+d^2}}{4},s<3+d$ ； $2+\frac{d+\sqrt{16+d^2}}{4}<r<4,s<\frac{dr\left(r-2\right)+r\left(r-1\right)}{\left(r-2\right)\left(r-1\right)}$。

综上， $F\left(0\right)<1$ 当且仅当 $r,s,\delta$ 满足以下任意条件：

a) $1+\frac{d}{3}<r<\frac{3+d}{2},\frac{dr}{r-1}<s<3+d.$

b) $\frac{3+d}{2}<r<4,\frac{dr}{r-1}<s<\frac{dr+r}{r-1}.$

c) $\frac{3+d}{2}<r<2+\frac{d+\sqrt{16+d^2}}{4},\frac{dr+r}{r-1}<s<3+d,\delta >\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)}.$

d) $2+\frac{d+\sqrt{16+d^2}}{4}<r<4,\delta >\frac{dr\left[r-s\left(r-1\right)+dr\right]}{\left(r-2\right)\left[s\left(r-1\right)-dr\right]-r\left(r-1\right)},\frac{dr+r}{r-1}<s<\frac{dr\left(r-2\right)+r\left(r-1\right)}{\left(r-2\right)\left(r-1\right)}.$

$F\left(0\right)<1$ 的情况讨论完毕。

特征方程同时满足 $F\left(1\right)>0,F\left(-1\right)>0,F\left(0\right)<1$ 时正不动点局部渐近稳定，则对以上条件求交集可得正不动点局部渐近稳定时参数的取值范围。

当特征方程满足 $F\left(1\right)>0,F\left(-1\right)=0$ 时，正不动点的特征值满足 ${\lambda }_1=-1$ 或 ${\lambda }_2=-1$，正不动点可能发生倍周期分支，由于 $F\left(1\right)>0$ 恒成立，计算得到 $s=\frac{\left(dr+2r\right)\left[s\left(r-1\right)+r\right]}{\left[\delta \left(r-3\right)+dr\right]\left(r-1\right)+4r}$ 时满足 $F\left(-1\right)=0$，通过观察我们发现在 $\delta =0,s=\frac{dr\left(d+2\right)}{d\left(r-1\right)+4}$ 时 $F\left(-1\right)=0$，假设此时 ${\lambda }_1=-1$，在此基础上通过计算可以发现另一个特征值 ${\lambda }_2<1$，于是 $\delta =0,s=\frac{dr\left(d+2\right)}{d\left(r-1\right)+4}$ 时正不动点处发生倍周期分支。

当特征方程满足 $F\left(1\right)>0,F\left(0\right)=1$ 且 $\Delta <0$ 时，正不动点的特征值 ${\lambda }_1,{\lambda }_2$ 为一对共轭复数，此时正不动点发生Neimark-Sacker分支，产生不变环。计算得到 $s=\frac{r\left[\delta \left(r-1\right)+dr\right]+dr\left[\delta \left(r-2\right)+dr\right]}{\left(r-1\right)\left[\delta \left(r-2\right)+dr\right]}$ 时满足 $F\left(0\right)=1$，通过观察我们发现在 $\delta =0$ 且 $s=\frac{dr+r}{r-1}$ 时满足 $F\left(0\right)=1$，同时，在该条件下特征方程的 $\Delta <0$，那么在 $\delta =0,s=\frac{dr+r}{r-1}$ 时正不动点处发生Neimark-Sacker分支。

3. 空间模型

3.1. 模型的建立

在本节将选取余弦核函数作为扩散核建立积分差分方程，利用可分离核的性质将无限维的积分差分方程模型简化为有限维差分方程组，以探究空间扩散因素对模型动力学的影响。首先引入余弦核函数，可得积分差分方程如下：

$\{\begin{array}{l}{N}_{t+1}\left(x\right)={\displaystyle {\int }_{\Omega }{K}_N}\left(x,y\right)r{N}_t\left(y\right)\left(1-N_t\left(y\right)-P_t\left(y\right)\right)\text{d}y,\hfill \\ P_{t+1}\left(x\right)={\displaystyle {\int }_{\Omega }{K}_P}\left(x,y\right)\left[s{N}_t\left(y\right)P_t\left(y\right)+\left(1-d\right)P_t\left(y\right)-\delta P_t{\left(y\right)}^2\right]\text{d}y.\hfill \end{array}$ (6)

其中余弦核为：

$K_N\left(x,y\right)=\{\begin{array}{l}\frac{\pi }{4R_N}\cos \frac{\pi }{2R_N}\left(x-y\right),\left|x-y\right|<R,\hfill \\ 0,\left|x-y\right|\ge R.\hfill \end{array}$

$K_P\left(x,y\right)=\{\begin{array}{l}\frac{\pi }{4R_P}\cos \frac{\pi }{2R_P}\left(x-y\right),\left|x-y\right|<R,\hfill \\ 0,\left|x-y\right|\ge R.\hfill \end{array}$

$R_N,R_P$ 分别为被捕食者的扩散半径和捕食者的扩散半径，假设 $R_P>R_N$，取空间域为一维有界同质区域 $\Omega$，设其长度为L，则 $\Omega =\left[-\frac{L}{2},\frac{L}{2}\right]$，我们假设捕食者和被捕食者都可以从空间域的一点移动到其他任意一点，即扩散半径和空间域大小需满足 $L\le R_N\le R_P$。

令 $L=R_P\tilde{L},R=\frac{R_N}{R_P}$，将方程(6)无量纲化并仍用L表示。得到

$\{\begin{array}{l}{N}_{t+1}\left(x\right)={\displaystyle {\int }_{-\frac{L}{2}}^{\frac{L}{2}}\frac{\pi }{4R}}\cos \frac{\pi }{2R}\left(x-y\right)r{N}_t\left(y\right)\left(1-N_t\left(y\right)-P_t\left(y\right)\right)\text{d}y,\hfill \\ P_{t+1}\left(x\right)={\displaystyle {\int }_{-\frac{L}{2}}^{\frac{L}{2}}\frac{\pi }{4}}\cos \frac{\pi }{2}\left(x-y\right)\left[s{N}_t\left(y\right)P_t\left(y\right)+\left(1-d\right)P_t\left(y\right)-\delta P_t{\left(y\right)}^2\right]\text{d}y.\hfill \end{array}$ (7)

由于 $L\le R_N\le R_P$，方程(7)满足 $L\le R\le 1$。

根据三角和的公式，余弦核可分别化为：

$\frac{\pi }{4R}\cos \frac{\pi }{2R}\left(x-y\right)=\frac{\pi }{4R}\left(\cos \frac{\pi x}{2R}\cos \frac{\pi y}{2R}+\sin \frac{\pi x}{2R}\sin \frac{\pi y}{2R}\right),$

$\frac{\pi }{4}\cos \frac{\pi }{2}\left(x-y\right)=\frac{\pi }{4}\left(\cos \frac{\pi x}{2}\cos \frac{\pi y}{2}+\sin \frac{\pi x}{2}\sin \frac{\pi y}{2}\right).$

如果我们令某一时刻种群密度是两个核函数的线性组合

$\begin{array}{l}{N}_t\left(x\right)=a_t\cos \frac{\pi x}{2R}+b_t\sin \frac{\pi x}{2R},\\ P_t\left(x\right)=c_t\cos \frac{\pi x}{2}+d_t\sin \frac{\pi x}{2}.\end{array}$

将其代入(7)，比较等式左右两端核函数的系数并计算积分，可将无限维的积分差分方程组转化为四维差分方程组

$\{\begin{array}{l}{a}_{t+1}=\left({\phi }_1-{\phi }_2{a}_t-{\phi }_3{c}_t\right)a_t-{\phi }_4{b}_t^2-{\phi }_5{b}_t{d}_t,\hfill \\ b_{t+1}=\left({\phi }_6-{\phi }_7{a}_t\right)b_t-{\phi }_8{b}_t{c}_t-{\phi }_9{a}_t{d}_t,\hfill \\ c_{t+1}={\phi }_{10}{a}_t{c}_t+{\phi }_{11}{b}_t{d}_t+{\phi }_{12}{c}_t-{\phi }_{13}{c}_t^2-{\phi }_{14}{d}_t^2,\hfill \\ d_{t+1}={\phi }_{15}{b}_t{c}_t+{\phi }_{16}{a}_t{d}_t+{\phi }_{17}{d}_t-{\phi }_{18}{c}_t{d}_t.\hfill \end{array}$ (8)

其中

${\phi }_1=r\left[\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right],$

${\phi }_2=r\sin \frac{\pi L}{4R}\left[1-\frac{1}{3}{\sin }^2\left(\frac{\pi L}{4R}\right)\right],$

${\phi }_3=\frac{r}{4}\left[\frac{1}{R}\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{R-2}\sin \left(\frac{\pi L\left(R-2\right)}{4R}\right)+\frac{1}{R+2}\sin \left(\frac{\pi L\left(R+2\right)}{4R}\right)\right],$

${\phi }_4=\frac{r}{3}{\sin }^3\left(\frac{\pi L}{4R}\right),$

${\phi }_5=\frac{r}{4}\left[\frac{1}{R-2}\sin \left(\frac{\pi L\left(R-2\right)}{4R}\right)-\frac{1}{R+2}\sin \left(\frac{\pi L\left(R+2\right)}{4R}\right)\right],$

${\phi }_6=r\left[\frac{\pi L}{8R}-\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right],$

${\phi }_7=\frac{2r}{3}{\sin }^3\left(\frac{\pi L}{4R}\right),$

${\phi }_8=\frac{r}{2}\left[\frac{2}{R}\sin \left(\frac{\pi L}{4R}\right)-\frac{1}{R-2}\sin \left(\frac{\pi L\left(R-2\right)}{4R}\right)-\frac{1}{R+2}\sin \left(\frac{\pi L\left(R+2\right)}{4R}\right)\right],$

${\phi }_9=\frac{r}{4}\left[\frac{1}{R-2}\sin \left(\frac{\pi L\left(R-2\right)}{4R}\right)-\frac{1}{R+2}\sin \left(\frac{\pi L\left(R+2\right)}{4R}\right)\right],$

${\phi }_{10}=\frac{sR}{4}\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right],$

${\phi }_{11}=\frac{sR}{4}\left[\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)-\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right],$

${\phi }_{12}=\left(1-d\right)\left(\frac{\pi L}{8}+\frac{1}{4}\sin \left(\frac{\pi L}{2}\right)\right),$

${\phi }_{13}=\delta \left[\sin \left(\frac{\pi L}{2}\right)-\frac{1}{3}{\sin }^3\left(\frac{\pi L}{2}\right)\right],$

${\phi }_{14}=\frac{\delta }{3}{\sin }^3\left(\frac{\pi L}{2}\right),$

${\phi }_{15}=\frac{sR}{4}\left[\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)-\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right],$

${\phi }_{16}=\frac{sR}{4}\left[2\sin \left(\frac{\pi L}{4R}\right)-\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)-\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right],$

${\phi }_{17}=\left(1-d\right)\left(\frac{\pi L}{8}-\frac{1}{4}\sin \left(\frac{\pi L}{2}\right)\right),$

${\phi }_{18}=\frac{2\delta }{3}{\sin }^3\left(\frac{\pi L}{4}\right).$

通过观察四维差分方程组(8)，我们发现 $\left\{b_t=0,d_t=0\right\}$ 为系统(8)的不变流形，在该不变流形上， $a_t,c_t$ 的方程与系统(3)相似。如果不变流形是吸引的，那么在该不变流形上，积分差分系统可以展示非空间系统的全部动力学行为。 $b_0,d_0=0$ 时一定有 $b_t=0,d_t=0$，此时不变流形是吸引的， $b_0,d_0\ne 0$ 时若能保证 $-1<{\phi }_6-{\phi }_7-{\phi }_8{c}_t<1$ 且 $-1<{\phi }_{16}{a}_t+{\phi }_{17}-{\phi }_{18}<1$，不变流形 $\left\{b_t=0,d_t=0\right\}$ 仍吸引，关于不变流形吸引的具体证明可参照Bramburger [17]。本文的主要目的是为了探究引入空间因素对模型动力学行为的影响，接下来我们的工作将限制在不变流形 $\left\{b_t=0,d_t=0\right\}$ 上。

3.2. 模型的分析

在不变流形 $\left\{b_t=0,d_t=0\right\}$ 上，四维差分方程组转化为以下形式

$\{\begin{array}{l}{a}_{t+1}=\left({\phi }_1-{\phi }_2{a}_t-{\phi }_3{c}_t\right)a_t,\hfill \\ c_{t+1}={\phi }_{10}{a}_t{c}_t+{\phi }_{12}{c}_t-{\phi }_{13}{c}_t^2.\hfill \end{array}$ (9)

下面我们在不变流形上取与系统(3)相关的不动点，分别为 $\left(0,0,0,0\right)$， $\left(\frac{{\phi }_1-1}{{\phi }_2},0,0,0\right)$， $\left(\frac{{\phi }_{13}\left({\phi }_1-1\right)+{\phi }_3\left(1-{\phi }_{12}\right)}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},0,\frac{{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},0\right)$。边界不动点的存在条件为 ${\phi }_1>1$，正不动点存在的条件为 ${\phi }_1>\frac{4-{\phi }_{12}}{3}$ 且 ${\phi }_{10}>\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}$。

定理3.1 对于模型(8)不动点的稳定性，有以下结论

$r_1=\frac{1}{\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)},r_2=\frac{4-{\phi }_{12}}{3\left[\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right]},r_3=\frac{3}{\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)},$

$r_4=\frac{4-{\phi }_{12}}{2\left[\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right]},r_5=\frac{9-{\phi }_{12}+\sqrt{17+{\phi }_{12}^2-2{\phi }_{12}}}{4\left[\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right]},$

$s^{*}=\frac{4{\phi }_2\left(4-{\phi }_{12}\right)}{R{\phi }_1\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right]},$

$s_1=\frac{4\left(1-{\phi }_{12}\right){\phi }_2}{R\left({\phi }_1-1\right)\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right]},$

$s_2=\frac{4\left[{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{R\left({\phi }_1-1\right)\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right]},$

$s_3=\frac{4\left[{\phi }_2\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)\left({\phi }_1-2\right)\right]}{R\left({\phi }_1-1\right)\left({\phi }_1-2\right)\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right]},$

$s_4=\frac{4\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2\right]}{R\left[\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4\right]\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right]},$

${\delta }_1=\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left\{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)\right\}\left[\sin \left(\frac{\pi L}{2}\right)-\frac{1}{3}{\sin }^3\left(\frac{\pi L}{2}\right)\right]},$

${\delta }_2=\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]\left[\sin \left(\frac{\pi L}{2}\right)-\frac{1}{3}{\sin }^3\left(\frac{\pi L}{2}\right)\right]}.$

1) 若 $r\in \left(0,r_1\right)$，则平凡不动点 $\left(0,0,0,0\right)$ 局部渐近稳定。

2) 若边界不动点 $\left(\frac{{\phi }_1-1}{{\phi }_2},0,0,0\right)$ 局部渐近稳定，则 $s,r$ 一定满足 $r\in \left(r_1,r_2\right),s<s^{*}$ 或者 $r\in \left(r_2,r_3\right),s<s_1$。

3) 若正不动点 $\left(\frac{{\phi }_{13}\left({\phi }_1-1\right)+{\phi }_3\left(1-{\phi }_{12}\right)}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},0,\frac{{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},0\right)$ 局部渐近稳定，则 $r,s,\delta$ 满足以下

任意条件

a) $r_2<r<r_4,s_1<s^{*}.$

b) $r_4<r<r_3,s_1<s<s_2.$

c) $r_4<r<r_3,s_2<s<s^{*},\delta >{\delta }_1.$

d) $r_3<r<r_5,s_2<s<s^{*},{\delta }_1<\delta <{\delta }_2.$

e) $r>r_5,s_2<s<s_3,{\delta }_1<\delta <{\delta }_2.$

f) $r>r_3,s_4<s<s_2,\delta <{\delta }_2.$

可给出模型不动点稳定性的分布图2：区域①中平凡不动点局部渐近稳定， $s,r$ 在区域②中为边界不动点局部渐近稳定的必要条件， $s,r$ 在区域③~⑥中为正不动点局部渐近稳定的必要条件。

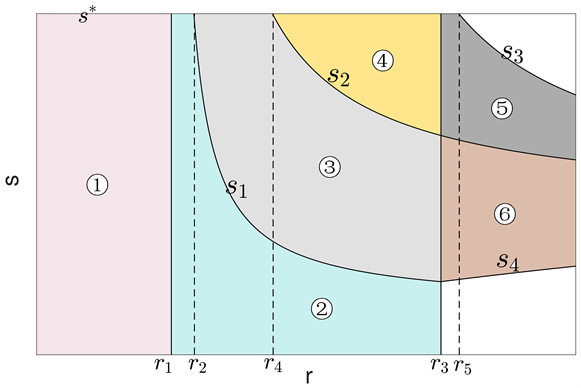
Figure 2. Stable interval distribution of immobile points when adding diffusion kernels

图2. 加入扩散核时不动点稳定区间分布

定理3.1的具体证明见附录。

通过对图1和图2的比较我们发现，在不变流形 $\left\{b_t,d_t=0\right\}$ 上，考虑空间因素的模型与非空间模型的动力学行为极为相似，两个模型不动点稳定性分布图大致相同，在相应的区间上对应的不动点的稳定性也相同，于是我们可以得到结论：引入空间因素，在不变流形上的某些参数平面基本不会在定性上改变模型的动力学行为。

通过 $r_1,r_2,r_3$ 的表达式可以看出，它们随着空间域L的增大而减小，也就是说随着空间域L的扩大，使得被捕食者独立存活或二者共存的r的值在减小，这也意味着在较大的空间域中，较小的被捕食者出

生率就可以使得捕食者独立存活或者二者共存。当 $R=\frac{R_N}{R_P}$ 增加，即被捕食者的扩散范围 $R_N$ 增加，或者

捕食者的扩散范围 $R_P$ 减小时， $r_1,r_2,r_3$ 增大，这意味着使得被捕食者持久或者二者共存的r要更大。这里可以得到与 [16] 相似的结论：捕食与被捕食模型的动力学是由有效猎物(即生长在该空间域内被捕食者)的生长速度决定的。那么r随着 $L,R$ 的变化可以得到很好解释，增大空间域的大小，那么因为扩散而离开该区域的被捕食者个体减小，生长在该空间域内被捕食者增多，就会增加被捕食者的有效生长速度，而被捕食者的扩散范围 $R_N$ 增大，离开该区域的被捕食者个体增加，被捕食者的有效生长速度减小，就需要更大的被捕食者生长速度才能使得捕食者独立存活或者二者共存。

由于 $s_1,s_4,s^{*}$ 的表达式非常复杂，难以直接判断其与 $L,R$ 的关系。固定其他参数值用matlab进行数值模拟，发现 $s_1,s_4,s^{*}$ 都随着L的增大而减小， $s^{*},s_4$ 随着R的增大而减小， $s_1$ 随着R的增大而增大。下面图3、图4分别给出参数 $L,R$ 增加时，不动点稳定性分布情况的变化。

Figure 3. The change in the stability interval when L increases

图3. L增大时稳定区间的变化

Figure 4. The change in the stability interval when R increases

图4. R增大时稳定区间的变化

4. 数值模拟

图5左上显示了，当 $r\in \left(0,1\right)$ 时，不考虑空间的模型(3)的解最终趋于 $\left(0,0\right)$，平凡不动点是稳定的。参数值为 $r=0.5$， $s=0.6$， $d=0.7$， $\delta =0.8$，同时取初值为 $N_0=0.5$， $P_0=0.3$。图5右上展示了在相同的初值状态下，当 $r\in \left(0,r_1\right)$ 时，考虑空间因素的模型(6)的平凡不动点也是局部渐近稳定的。此时我们取空间域 $L=0.7$，扩散范围 $R=0.8$，被捕食者的死亡率 $d=0.7$，那么将假设的 $L,R,d$ 代入，计算可得： $r_1\approx 1.7$， $r_3\approx 5.12$， ${\phi }_1\approx 0.87$， ${\phi }_2\approx 0.81$， ${\phi }_3\approx 0.64$， ${\phi }_{10}\approx 0.59$， ${\phi }_{12}\approx 0.14$， ${\phi }_{13}\approx 0.89$，那么我们取 $r=1.5$， $s=0.7$， $d=0.7$， $\delta =0.8$，进行数值模拟最终捕食者与被捕食者最终都将趋于灭绝。

图5左下展示了，不考虑空间因素的模型(3)的解最终区域边界不动点的情况，此时的参数值为

$r=1.1$， $s=2$， $d=0.6$， $\delta =0.8$ 同时初值为 $N_0=0.5$， $P_0=0.4$，此时解会趋于边界不动点 $\left(\frac{1}{11},0\right)$。

图5右下展示了，考虑空间因素时，被捕食者者独立存活，捕食者灭绝状态的情况，此时我们仍取空间域 $L=0.7$，扩散范围 $R=0.8$，r需在 $r_1$ 到 $r_3$ 之间，我们取 $r=3$，s要满足 $s<s_1\approx 3.1$，我们取 $s=3$， $d=0.7$， $\delta =0.8$，通过计算有 ${\phi }_1\approx 1.75$， ${\phi }_2\approx 1.62$， ${\phi }_3\approx 1.28$， ${\phi }_{10}\approx 1.36$， ${\phi }_{12}\approx 0.14$， ${\phi }_{13}\approx 0.89$。

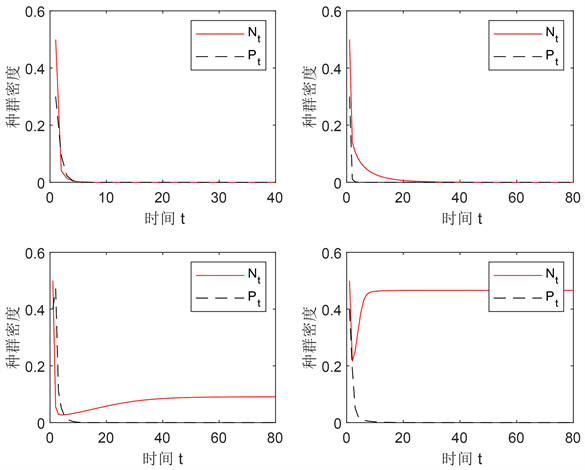
Figure 5. Numerical simulation of extinction states and boundary states

图5. 灭绝状态和边界状态的数值模拟

图6的四个图形分别展示了不考虑空间因素和考虑空间因素两类模型的解最终趋于共存状态的情况。图6左上，是模型(3)在参数值取 $r=2$， $d=0.6$， $\delta =0.8$， $1.2<s=2<3.2$， $N_0=0.5$， $P_0=0.4$ 时得到的。在模型(6)中，我们仍考虑空间域 $L=0.7$，扩散范围 $R=0.8$，被捕食者的死亡率 $d=0.7$，在 $r_1,r_3$ 之间取 $r=3$，与图5右下图的参数相同，带入计算有 ${\phi }_1\approx 1.75$， ${\phi }_2\approx 1.62$， ${\phi }_3\approx 1.28$， ${\phi }_{12}\approx 0.14$，但是这里我们取 $3.1<s<8.76$，取 $s=6$，那么 ${\phi }_{10}\approx 2.7$，我们发现在初值相同时，解最终将趋于正不动点。

图6左下，是模型(3)的模拟，首先在参数值 $d=0.6$ 的情况下我们可取 $3.16<r=3.5<4$，可以计算出s的取值范围为 $\left(2.24,3.17\right)$，我们取 $s=3$，那么又可以得到 $\delta$ 的取值范围 $\left(6.13,48\right)$，取 $\delta =10$，此时我们发现模型(3)的解趋于共存。在模型(6)中，首先取 $r=6>r_5\approx 5.53$， $d=0.7$， $\delta =0.7$，代入计算得到 ${\phi }_1\approx 3.51$， ${\phi }_2\approx 3.24$， ${\phi }_3\approx 2.56$， ${\phi }_{12}\approx 0.147$，通过计算可以得到s的取值范围为 $\left(5.25,7.22\right)$，我们取 $s=6$，那么有 ${\phi }_{10}\approx 2.73$，再计算得到 $\delta$ 的取值范围，我们取 $\delta =1$，于是有 ${\phi }_{13}\approx 1.12$，此时模拟得到的结果为捕食者与被捕食者共存。

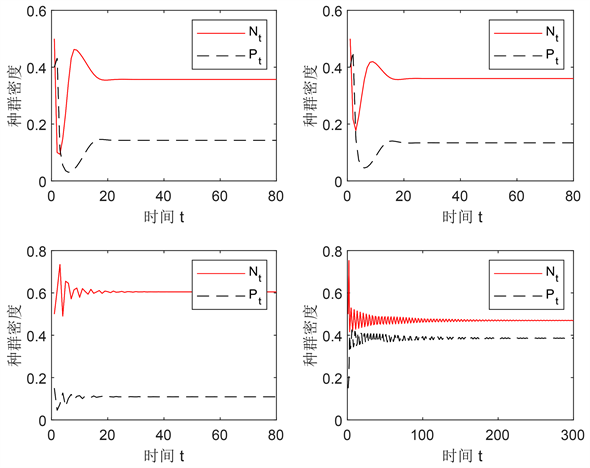
Figure 6. Numerical simulation of coexistence states

图6. 共存状态的数值模拟

5. 总结

本文首先建立了一个世代重叠的离散捕食与被捕食模型，讨论了该模型不动点的稳定性。再引入余弦核函数，建立了一个积分差分方程组，通过可分离核的性质将无限维积分差分模型简化为有限为差分方程组，并在不变流形上讨论了该模型与非空间模型对应的不动点的稳定性，探究空间因素对模型动力学的影响，发现引入空间因素在不变流形上不改变模型的定性性质，同时影响捕食者与被捕食者动力学的是被捕食者的有效增长率。

基金项目

本文得到国家自然科学基金(12171110)资助。

附录

下面给出定理3.1的证明。

证明：模型(8)的Jacobi矩阵为：

$J_2=\left(\begin{array}{cccc}\left({\phi }_1-{\phi }_2{a}_t-{\phi }_3{c}_t\right)-{\phi }_2{a}_t& -2{\phi }_{12}{b}_t-{\phi }_5{d}_t& -{\phi }_3{a}_t& -{\phi }_5{b}_t\\ -{\phi }_7{b}_t-{\phi }_9{d}_t& {\phi }_6-{\phi }_7{a}_t-{\phi }_8{c}_t& -{\phi }_8{b}_t& -{\phi }_9{a}_t\\ {\phi }_{10}{c}_t& {\phi }_{11}{d}_t& {\phi }_{10}{a}_t+{\phi }_{12}-2{\phi }_{13}{c}_t& {\phi }_{11}{b}_t-2{\phi }_{14}{d}_t\\ {\phi }_{16}{d}_t& {\phi }_{15}{c}_t& {\phi }_{15}{b}_t-{\phi }_{18}{d}_t& {\phi }_{16}{a}_t+{\phi }_{17}-{\phi }_{18}{c}_t\end{array}\right).$

首先证明 $\left(0,0,0,0\right)$ 的局部稳定性，在 $\left(0,0,0,0\right)$ 处的Jacobi矩阵为：

$J_{\left(0,0,0,0\right)}=\left(\begin{array}{cccc}{\phi }_1& 0& 0& 0\\ 0& {\phi }_6& 0& 0\\ 0& 0& {\phi }_{12}& 0\\ 0& 0& 0& {\phi }_{17}\end{array}\right).$

显然特征值 ${\lambda }_1={\phi }_1,{\lambda }_2={\phi }_6,{\lambda }_3={\phi }_{12},{\lambda }_3={\phi }_{17}$，观察 ${\phi }_1,{\phi }_6,{\phi }_{12},{\phi }_{17}$ 的表达式我们发现， $0\le {\phi }_6\le {\phi }_1$， $0\le {\phi }_{17}\le {\phi }_{12}$，所以 ${\phi }_1,{\phi }_{12}<1$ 时，平凡不动点 $\left(0,0,0,0\right)$ 局部渐近稳定。由于 ${\phi }_{12}<1$ 恒成立，只要 ${\phi }_1<1$ 即可，通过

${\phi }_1=r\left[\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right]<1,$

得到 $r<r_1,r_1=\frac{1}{\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)}$ 时 $\left(0,0,0,0\right)$ 局部渐近稳定。

再证明边界不动点的稳定性，在 $\left(\frac{{\phi }_1-1}{{\phi }_2},0,0,0\right)$ 处的Jacobi矩阵为

$J_{\left(\frac{{\phi }_1-1}{{\phi }_2},0,0,0\right)}=\left(\begin{array}{cccc}{\phi }_1-2{\phi }_2\frac{{\phi }_1-1}{{\phi }_2}& 0& -{\phi }_3\frac{{\phi }_1-1}{{\phi }_2}& 0\\ 0& {\phi }_{13}-{\phi }_{17}\frac{{\phi }_1-1}{{\phi }_2}& 0& -{\phi }_9\frac{{\phi }_1-1}{{\phi }_2}\\ 0& 0& {\phi }_{12}+{\phi }_{10}\frac{{\phi }_1-1}{{\phi }_2}& 0\\ 0& 0& 0& {\phi }_{17}+{\phi }_{16}\frac{{\phi }_1-1}{{\phi }_2}\end{array}\right).$

$J_{\left(\frac{{\phi }_1-1}{{\phi }_2},0,0,0\right)}$ 是一个上三角矩阵，特征值为对角线上的值，我们发现第一行和第三行的特征值与之前不加扩散核的特征值相对应，因此，我们着重讨论这两项。即边界不动点 $\left(\frac{{\phi }_1-1}{{\phi }_2},0,0,0\right)$ 局部渐近稳定的必要条件为 $\left|2-{\phi }_1\right|<1,\left|{\phi }_{12}+{\phi }_{10}\frac{{\phi }_1-1}{{\phi }_2}\right|<1$。简单计算上述不等式，得到取值范围 $1<{\phi }_1<\frac{4-{\phi }_{12}}{3}$， $0<{\phi }_{10}<\frac{{\phi }_2\left(4-{\phi }_{12}\right)}{{\phi }_1}$ 或 $\frac{4-{\phi }_{12}}{3}<{\phi }_1<3$， $0<{\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}$。 ${\phi }_1,{\phi }_{10}$ 分别线性依赖于 $r,s$，将 ${\phi }_1,{\phi }_{10}$ 的表达式带入，可得边界不动点局部渐近稳定时 $r,s$ 满足以下任一条件： $r_2<r<r_3,0<s<s_1$ 或 $r_1<r<r_2,0<s<s^{*}$ 其中

$r_2=\frac{4-{\phi }_{12}}{3\left[\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)\right]},r_3=\frac{3}{\frac{\pi L}{8R}+\frac{1}{4}\sin \left(\frac{\pi L}{2R}\right)},$

$s^{*}=\frac{4{\phi }_2\left(4-{\phi }_{12}\right)}{R{\phi }_{1}2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)},$

$s_1=\frac{4\left(1-{\phi }_{12}\right){\phi }_2}{R\left({\phi }_1-1\right)\left[2\sin \left(\frac{\pi L}{4R}\right)+\frac{1}{2R-1}\sin \left(\frac{\pi L\left(2R-1\right)}{4R}\right)+\frac{1}{2R+1}\sin \left(\frac{\pi L\left(2R+1\right)}{4R}\right)\right]},$

最后证明正不动点的稳定性，将正不动点记作 $\left(a^{*},0,c^{*},0\right)$，在正不动点处的Jacobi矩阵 $J_{\left(a^{*},0,c^{*},0\right)}$ 为

$\left(\begin{array}{cccc}\left({\phi }_1-{\phi }_2{a}^{*}-{\phi }_3{c}^{*}\right)-{\phi }_2{a}^{*}& 0& -{\phi }_3{a}^{*}& 0\\ 0& {\phi }_6-{\phi }_7{a}^{*}-{\phi }_8{c}^{*}& 0& -{\phi }_9{a}^{*}\\ {\phi }_{10}{c}^{*}& 0& {\phi }_{10}{a}^{*}+{\phi }_{12}-2{\phi }_{13}{c}^{*}& 0\\ 0& {\phi }_{15}{c}^{*}& 0& {\phi }_{16}{a}^{*}+{\phi }_{17}-{\phi }_{18}{c}^{*}\end{array}\right).$

四阶矩阵 $J_{\left(a^{*},0,c^{*},0\right)}$ 特征值非常复杂，但由于我们是在不变流形 $\left\{b_t=0,d_t=0\right\}$ 上考虑，这里可将四阶

矩阵减少为以下二阶矩阵

$\left(\begin{array}{cc}1-{\phi }_2{a}^{*}& -{\phi }_3{a}^{*}\\ {\phi }_{10}{c}^{*}& 1-{\phi }_{13}{c}^{*}\end{array}\right).$

其特征方程为

$F\left(\lambda \right)={\lambda }^2-\left(1-{\phi }_2{a}^{*}+1-{\phi }_{13}{c}^{*}\right)\lambda +1-{\phi }_2{a}^{*}-{\phi }_{13}{c}^{*}+\left({\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}\right)a^{*}{c}^{*}.$ (10)

首先讨论满足 $F\left(1\right)>0$ 时的情况，将 $\lambda =1$ 带入特征方程(10)有

$F\left(1\right)=\frac{\left[{\phi }_{13}\left({\phi }_1-1\right)+{\phi }_3\left(1-{\phi }_{12}\right)\right]\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},$

在 ${\phi }_1>\frac{4-{\phi }_{12}}{3}$ 且 ${\phi }_{10}>\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}$ 时， $F\left(1\right)>0$ 恒成立。

再讨论满足 $F\left(-1\right)>0$ 时的情况，将 $\lambda =-1$ 带入特征方程(10)有

$\begin{array}{c}F\left(-1\right)=4-2{\phi }_2{a}^{*}-2{\phi }_{13}{c}^{*}+\left({\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}\right)a^{*}{c}^{*}\\ =\frac{\left[{\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)\right]\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},\end{array}$

其中 ${\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)>0$，下面进行分类讨论：

若 ${\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2>0$ 即 ${\phi }_{10}>\frac{{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2}{{\phi }_1-1}$ 时，由于 ${\phi }_{10}$ 同时还满足 ${\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right)$，经过计算在 ${\phi }_1=4-{\phi }_{12}$ 时， ${\phi }_{10}=\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right)=\frac{{\phi }_2\left(1-{\phi }_{12}+2{\phi }_2\right)}{{\phi }_1-1}$。 ${\phi }_1=4-{\phi }_{12}>3$，此时 $F\left(-1\right)>0$ 恒成立。

若 ${\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2<0$ 即 $1<{\phi }_1<4-{\phi }_{12}$， ${\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right)$ ； ${\phi }_1>4-{\phi }_{12}$， ${\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2}{{\phi }_1-1}$ 在此条件下仍有两种情况：

若满足 ${\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)<0$，在此条件下 $F\left(-1\right)>0$ 恒成立，即 $1<{\phi }_1<3$ 且 ${\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)}{3-{\phi }_1}$。

若满足 ${\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)>0$ 时，要更复杂一些，还需要继续进行分类讨论：

若 ${\phi }_1>3$，自然有 ${\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)>0$，此时

要

$4{\phi }_3{\phi }_{10}>-\left[{\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)\right]\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]$

才有 $F\left(-1\right)>0$，通过计算可得

${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

同时，为了保证种间竞争率 $\delta$ 始终为正， ${\phi }_{13}$ 也需始终为正，

$\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}>0,$

保证分子 ${\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}>0$ 可得

${\phi }_{10}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}.$

即

$3<{\phi }_1<4-{\phi }_{12},\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right),$

${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]},$

或者

${\phi }_1>4-{\phi }_{12},\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}<{\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2}{{\phi }_1-1},$

${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

时有 $F\left(-1\right)>0$。

若 $1<{\phi }_1<3$，此时只有满足 ${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)}{3-{\phi }_1}$ 才有 ${\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)>0$，根据前面的计算，在这

种情况下

${\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}$

且

${\phi }_{10}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}$

才有 $F\left(-1\right)>0$。通过计算我们发现当 ${\phi }_1=3$ 时，

${\phi }_{10}=\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}=\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1},$

$1<{\phi }_1<3$ 时，后者更大， ${\phi }_1>3$ 时，前者更大。也就是说满足 $1<{\phi }_1<3,{\phi }_{10}>\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}$ 情况下， ${\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}>0$ 恒成立，即 ${\phi }_{13}$ 大于一个负数即可，同时 ${\phi }_{13}$ 恒为正，只要取 $0<{\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)}{3-{\phi }_1}$ 就有 $F\left(-1\right)>0$。

综上， $F\left(-1\right)>0$ 当且仅当 ${\phi }_1,{\phi }_{10},{\phi }_{13}$ 满足以下任意条件

${\phi }_1>4-{\phi }_{12},\frac{{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right).$

a) $3<{\phi }_1<4-{\phi }_{12},\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right),$ ${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

b) ${\phi }_1>4-{\phi }_{12},\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_3\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}<{\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2}{{\phi }_1-1},$ ${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

c) $\frac{4-{\phi }_{12}}{3}<{\phi }_1<3,\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right).$

最后讨论满足 $F\left(0\right)<1$ 时的情况，将 $\lambda =0$ 带入特征方程(10)有

$\begin{array}{l}F\left(0\right)=1-{\phi }_2{a}^{*}-{\phi }_{13}{c}^{*}+\left({\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}\right)a^{*}{c}^{*}\\ =1+\frac{\left[{\phi }_{13}\left({\phi }_1-1\right)+{\phi }_3\left(1-{\phi }_{12}\right)\right]\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left[{\phi }_{13}\left({\phi }_1-1\right)+{\phi }_3\left(1-{\phi }_{12}\right)\right]-{\phi }_{13}\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]}{{\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}},\end{array}$

$F\left(0\right)<1$ 即，

由于 ${\phi }_2{\phi }_{13}+{\phi }_3{\phi }_{10}$ 始终为正，满足下式即可

其中 ${\phi }_{13}\left({\phi }_1-3\right)+{\phi }_3\left(1-{\phi }_{12}\right)>0,{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)>0$。下面进行分类讨论：

若 ${\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-{\phi }_2<0$，即 ${\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}$。根据不等式左边各项的正负性，易得 $F\left(0\right)<1$ 成立。由于 ${\phi }_{10}=\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}$ 与 ${\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right)$ 相交与 ${\phi }_1=\frac{4-{\phi }_{12}}{2},{\phi }_{10}$ 的范围有所限制。

若 ${\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-{\phi }_2>0$，即 ${\phi }_{10}>\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}$。此时不能直接判断出 $F\left(0\right)$ 与1的大小关系，换一种合并同类项方式 $F\left(0\right)<1$ 可转化为下式：

${\phi }_{13}\left\{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)\right\}+{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-{\phi }_2\right]<0$

再进行分类讨论：

如果 $1<{\phi }_1<2$，同时 ${\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)}$，那么 $F\left(0\right)<1$。

如果 ${\phi }_1>2$，同时有

${\phi }_{10}<\frac{{\phi }_2\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)\left({\phi }_1-2\right)}{\left({\phi }_1-1\right)\left({\phi }_1-2\right)},$

${\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)},$

可保证 $F\left(0\right)<1$。同时我们还要注意，取得的范围需满足 $\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right)$。通过简单计算可知， ${\phi }_{10}=\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}$ 和 ${\phi }_{10}=\frac{{\phi }_2\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right){\phi }_3}{\left({\phi }_1-1\right)\left({\phi }_1-2\right)}$ 分别与 ${\phi }_{10}=\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right)$ 相交于 ${\phi }_1=\frac{4-{\phi }_{12}}{2}$ 和 ${\phi }_1=\frac{10-{\phi }_{12}+\sqrt{36+{\phi }_{12}^2-4{\phi }_{12}}}{4}$。

综上， $F\left(0\right)<1$ 当且仅当 ${\phi }_1,{\phi }_{10},{\phi }_{13}$ 满足以下任意条件

$\frac{4-{\phi }_{12}}{2}<{\phi }_1<\frac{9-{\phi }_{12}+\sqrt{17+{\phi }_{12}^2-2{\phi }_{12}}}{4},\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right),$

${\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)}.$

a) ${\phi }_1>\frac{9-{\phi }_{12}+\sqrt{17+{\phi }_{12}^2-2{\phi }_{12}}}{4},{\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)},$ $\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)\left({\phi }_1-2\right)}{\left({\phi }_1-1\right)\left({\phi }_1-2\right)}.$

b) $\frac{4-{\phi }_{12}}{3}<{\phi }_1<\frac{4-{\phi }_{12}}{2},\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right).$

c) ${\phi }_1>\frac{4-{\phi }_{12}}{2},\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}.$

对以上使得特征方程满足 $F\left(1\right)>0,F\left(-1\right)>0,F\left(0\right)<1$ 的条件求交集，即可得到正不动点局部渐近稳定的必要条件：

A) $\frac{4-{\phi }_{12}}{3}<{\phi }_1<\frac{4-{\phi }_{12}}{2},\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right).$

B) $\frac{4-{\phi }_{12}}{2}<{\phi }_1<3,\frac{{\phi }_2\left(1-{\phi }_{12}\right)}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}.$

C) $\frac{4-{\phi }_{12}}{2}<{\phi }_1<3,\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right),$ ${\phi }_{13}>\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)}.$

D) $3<{\phi }_1<\frac{9-{\phi }_{12}+\sqrt{17+{\phi }_{12}^2-2{\phi }_{12}}}{4},\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2}{{\phi }_1}\left(4-{\phi }_{12}\right),$ $\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)}<{\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

E) ${\phi }_1>\frac{9-{\phi }_{12}+\sqrt{17+{\phi }_{12}^2-2{\phi }_{12}}}{4},\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1}<{\phi }_{10}<\frac{{\phi }_2\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)\left({\phi }_1-2\right)}{\left({\phi }_1-1\right)\left({\phi }_1-2\right)},$ $\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[-{\phi }_{10}\left({\phi }_1-1\right)+{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2\right]}{\left({\phi }_1-2\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)\right]-{\phi }_2\left({\phi }_1-1\right)}<{\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

F) ${\phi }_1>3,\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_2\left(1-{\phi }_{12}\right)+2{\phi }_2\right]}{{\phi }_3\left(1-{\phi }_{12}\right)\left({\phi }_1-1\right)+4{\phi }_3}<{\phi }_{10}<\frac{{\phi }_2\left(1-{\phi }_{12}\right)+{\phi }_2}{{\phi }_1-1},$ ${\phi }_{13}<\frac{{\phi }_3\left(1-{\phi }_{12}\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]+4{\phi }_3{\phi }_{10}}{\left(3-{\phi }_1\right)\left[{\phi }_{10}\left({\phi }_1-1\right)-{\phi }_2\left(1-{\phi }_{12}\right)-2{\phi }_2\right]}.$

根据 ${\phi }_1,{\phi }_{10},{\phi }_{13}$ 的表达式，我们可以发现它们分别线性依赖于 $r,s,\delta$，将 ${\phi }_1,{\phi }_{10},{\phi }_{13}$ 的表达式分别带入上述A~F式中，可以得到关于 $r,s,\delta$ 的取值范围。

NOTES

^*通讯作者。