有界分红下带风险投资的复合Poisson-Geometric风险模型

A Compound Poisson-Geometric Risk Model with Risk Investment and Barrier Dividend

摘要: 在考虑了保费收入为混合保费以及保险公司将多余资本用于投资来提高其赔付能力的基础上，文章首先建立随机保费收入服从复合Poisson过程，理赔量服从复合Poisson-Geometric过程且带风险投资和分红的风险模型。然后运用全期望公式与积分变换公式，得到了该模型的期望红利现值函数满足的微–积分方程及特定分布下满足的微分方程与解析解，最后通过数值模拟和算例分析了模型关键参数对期望红利现值函数的影响，得出红利现值函数是关于初始资本、风险投资额、固定保费收入、平均保费额的增函数，是关于偏离系数、平均索赔额的减函数，验证了文章得出的结果是合理的。

Abstract: Taken into account the effects of random interference because of the premiums’ randomness and mixed premium in insurance business, and used the surplus capital to invest in order to enhance the insurance payment level. We defined the risk investment and barrier dividend risk model with interference in which the random premium income follows the compound Poisson process and the claim numbers follow a compound Poisson-Geometric process. The integral-differential equation of expectation function about expected discounted dividend payment has been given by the method of total expectation formula and integral transform. In the special case, the closed form solution of the expectation formula about cumulative dividends is obtained. Finally, to illustrate the reasonableness of the obtained theoretical results, the influence of key parameters of the model on the expected dividend present value function is analyzed by numerical simulation and examples, the present value function of dividends is an increasing function of initial capital, venture capital, fixed premium income, average premium amount, and a decreasing function of deviation coefficient and average claim amount.

1. 引言

在保险公司的实际业务中，当盈余达到红利边界后，保险公司把超出红利边界的部分盈余给投保者进行分红，从而提高自身在保险行业的竞争力。1957年，Finetti首次研究了分红问题，随后分红问题逐渐成为保险精算领域研究的热点问题之一 [1] [2] [3] [4]。由于经典的分红模型中未考虑风险投资带来的收益，而保险公司为了提高自身的竞争力通常会拿一部分资金进行风险投资，所以本文加入随机变量表示风险投资额和风险投资带来的收益。此外，在经典风险模型中，假设保险公司在单位时间内收到的保费是某一固定常数或者是随机保费，但是在实际的业务中，保险公司可能跟一些投保人签订协议，在每个单位时间内投保人都会定期缴纳固定的保费，所以本文讨论的是同时带有随机保费和固定保费收入的风险模型。在经典风险模型中，假设索赔次数是服从均值与方差相等的Poisson分布，但是实际上索赔次数并不完全服从Poisson分布。例如当保险公司出台免赔额、无赔款折扣制度之后，就并不是所有的事故发生都可以得到索赔，此时索赔次数就会小于事故发生次数，方差大于均值。为了改进和优化经典风险模型，毛泽春 [5] 引出了索赔次数服从复合Poisson-Geometric过程的风险模型。近年来，该模型也得到许多学者的关注，如文献 [6] [7] [8] 讨论的是复合Poisson-Geometric风险模型的Gerber-Shiu罚金函数，文献 [9] - [15] 研究Poisson-Geometric风险模型的分红问题，并且取得一定的成果。

基于以上的研究现状，本文在文献 [15] 模型的基础上，做了如下的推广：首先增加了风险投资因素及保费收取同时为固定保费和随机保费的混合保费过程，其中固定保费是服从线性增长过程，随机保费是服从复合Poisson过程，索赔过程是服从复合Poisson-Geometric计数过程的风险模型。然后利用全概率公式与积分变换公式研究该模型的期望红利现值函数满足的微–积分方程及特定分布下满足的微分方程与解析解。最后为了验证文章结果的合理性，通过数值模拟和算例分析模型关键参数对红利现值函数的影响，得到深刻的经济见解。

本文的结构安排为如下：第一节给出了模型的建立及其介绍；第二节主要是本研究主要结论的证明过程；第三节数值模拟分析模型关键参数对红利现值函数的影响；第4节给出结论。

2. 模型的建立及介绍

假设所有的随机变量和随机过程均定义在概率空间 $\left(\Omega ,\mathcal{F},P\right)$ 上，下面先给出盈余过程、索赔次数、分红策略及红利现值函数的数学描述。

定义1 [5] 若随机变量 $\zeta$ 的母函数为

$G\left(t\right)=\exp \left\{\frac{\lambda \left(t-1\right)}{1-\rho t}\right\}$

则称母函数 $G\left(t\right)$ 所对应的分布为复合Poisson-Geometric分布，记为 $PG\left(\lambda ,\rho \right)$ ，其中 $\lambda >0,0\le \rho <1$ 。

引理1 [5] 若随机变量 $\zeta$ 的母函数 $G\left(t\right)$ ， $\lambda >0,0\le \rho <1$ ，则 $\zeta$ 的矩母函数为

$M_{\zeta }\left(r\right)=\exp \left\{\frac{\lambda \left({\text{e}}^r-1\right)}{1-\rho {\text{e}}^r}\right\}$

注1当 $\rho =0$ 时，复合Poisson-Geometric分布就是Poisson分布， $\rho$ 称为偏离系数。

定义2 [5] 设 $\lambda >0,0\le \rho <1$ ，称随机过程 $\left\{N\left(t\right),t\ge 0\right\}$ 为参数为 $\lambda ,\rho$ 的复合Poisson-Geometric过程，如果满足

1) $N\left(0\right)=0$ ；

2) $\left\{N\left(t\right),t\ge 0\right\}$ 具有独立平稳增量；

3) 对 $t>0$ ，有 $N\left(t\right)\sim PG\left(\lambda t,\rho \right)$ ，且

$E\left[N\left(t\right)\right]=\frac{\lambda t}{1-\rho }$ ， $Var\left[N\left(t\right)\right]=\frac{\lambda t\left(1+\rho \right)}{{\left(1-\rho \right)}^2}$

4) $N\left(t\right)$ 的矩母函数为

$M_{N\left(t\right)}\left(r\right)=\exp \left\{\frac{\lambda t\left({\text{e}}^r-1\right)}{1-\rho {\text{e}}^r}\right\}$

注2：在定义2中，当 $\rho =0$ 时，复合Poisson-Geometric过程就是Poisson过程。

在本研究中，假设的索赔计数次数也满足复合Poisson-Geometric计数过程。

定义3 保险公司盈余过程为

$U\left(t\right)=\left(u-F\right)+\left(1+tj\right)F+ct+{\displaystyle \underset{k=1}{\overset{M\left(t\right)}{\sum }}{X}_k}-{\displaystyle \underset{k=1}{\overset{N_1\left(t\right)}{\sum }}{Y}_k}+\sigma FW\left(t\right),t\ge 0$ (1)

盈利过程为

$S\left(t\right)=tjF+ct+{\displaystyle \underset{k=1}{\overset{M\left(t\right)}{\sum }}{X}_k}-{\displaystyle \underset{k=1}{\overset{N_1\left(t\right)}{\sum }}{Y}_k}+\sigma FW\left(t\right),t\ge 0$ (2)

其中，u为初始准备金，F是投资额，j是单位时间内风险投资收益率，c是单位时间内保险公司收到固

定的保费， $\left\{W\left(t\right),t\ge 0\right\}$ 是标准的布朗运动， $\sigma$ 为单位波动率； ${\displaystyle \underset{k=1}{\overset{M\left(t\right)}{\sum }}{X}_k}$ 表示 $\left(0,t\right]$ 时间内保险公司收到的

随机总保费额，计数过程 $M\left(t\right)$ 表示签订的随机保单数服从参数为 ${\lambda }^{*}t$ 的复合Poisson过程； $X_k$ 表示第k次收到的随机保费额，其分布函数用 $F\left(x\right)$ 表示，密度函数用 $f\left(x\right)$ 表示， $\bar{F}\left(x\right)=1-F\left(x\right)$ 是 $F\left(x\right)$ 的尾函

数； ${\displaystyle \underset{k=1}{\overset{N_1\left(t\right)}{\sum }}{Y}_k}$ 表示 $\left(0,t\right]$ 时间内保单发生的总索赔额，计数过程 $N_1\left(t\right)$ 表示索赔的保单数且服从参数为 $\left({\lambda }_{1}t,{\rho }_1\right)$ $\left({\lambda }_1>0,0\le {\rho }_1\le 1\right)$ 的复合Poisson-Geometric过程， $E\left[N_1\left(t\right)\right]=\frac{{\lambda }_{1}t}{1-{\rho }_1}$ ， $Var\left[N_1\left(t\right)\right]=\frac{{\lambda }_{1}t\left(1+{\rho }_1\right)}{{\left(1-{\rho }_1\right)}^2}$ ；

$Y_k$ 表示第k次理赔的理赔金额，其分布函数分别为 $G\left(y\right)$ ，密度函数为 $g\left(y\right)$ 且 $\bar{G}\left(y\right)=1-G\left(y\right)$ 。本文假设保险公司收取保费、赔付、支付红利均在时间区间 $\left(t-1,t\right]$ 的始端进行，且 $\left\{X_k,k\ge 0\right\}$ ， $\left\{Y_k,k\ge 0\right\}$ ， $\left\{M\left(t\right),t\ge 0\right\}$ ， $\left\{N_1\left(t\right),t\ge 0\right\}$ ， $\left\{W\left(t\right),t\ge 0\right\}$ 之间是相互独立的。

为了保证保险公司的正常运行，须保证收入总和大于支出总和，即

$\begin{array}{c}E\left[S\left(t\right)\right]=E\left[tjF+ct+{\displaystyle \underset{k=1}{\overset{M\left(t\right)}{\sum }}{X}_k}-{\displaystyle \underset{k=1}{\overset{N_1\left(t\right)}{\sum }}{Y}_k}+\sigma W\left(t\right)\right]\\ =tjF+ct+E\left[M\left(t\right)\right]E\left[X_k\right]-E\left[N_1\left(t\right)\right]E\left[Y_k\right]\\ =\left(jF+c+{\lambda }^{*}\mu -\frac{{\lambda }_1{\mu }_1}{1-{\rho }_1}\right)t>0\end{array}$

因为 $t>0$ ，所以 $jF+c+{\lambda }^{\text{*}}\mu -\frac{{\lambda }_1{\mu }_1}{1-{\rho }_1}>0$ 。

相对安全负荷系数为

$\theta =\frac{jF+c+{\lambda }^{\text{*}}\mu }{\frac{{\lambda }_1{\mu }_1}{1-{\rho }_1}}-1$ ，

设红利界为b，当盈余小于b时不发放红利，当大于b时，超出的部分全部发放红利。此时定义红利过程 $D\left(t\right)$ 在时刻t的总红利现值为 $D_{u,b}\left(t\right)={\displaystyle {\int }_0^{T_{u,b}}{\text{e}}^{-\delta t}}\text{d}D\left(t\right)$ ，记 $T_{u,b}=\inf \left\{t\ge 0,U_b\left(t\right)<0|U_b\left(0\right)=u\right\}$ 为破产时刻， $\delta \ge 0$ 为贴现率，盈余过程为 $U_b\left(t\right)=U\left(t\right)-D_{u,b}\left(t\right)$ 。

定义4保险公司总红利现值的期望为

$V\left(u;b\right)=E\left[D_{u,b}\left(t\right)|U_b\left(0\right)\right]$ ， $0\le u\le b$

引理2 [5] 设 $\left\{N_1\left(t\right),t\ge 0\right\}$ 是满足模型(1)的复合Poisson-Geometric过程，记 ${\alpha }_1=\frac{{\lambda }_1\left(1-{\rho }_1\right)}{{\rho }_1}$ (若 ${\rho }_1=0$ ，则取 ${\alpha }_1={\lambda }_1$ )，则当 $t\to 0$ 时，有

$\mathrm{Pr}\left(N_1\left(t\right)=0\right)={\text{e}}^{-{\lambda }_{1}t}=1-{\lambda }_{1}t+o\left(t\right)$ ，

$\mathrm{Pr}\left(N_1\left(t\right)=k\right)={\alpha }_1{\rho }_1^{k}t+A_{1k}\left(t\right)o\left(t\right),k=1,2,\cdots$ ，

其中

$A_{1k}\left(t\right)={\rho }_1^k+\left(k-1\right){\left[{\rho }_1\left(1+{\alpha }_{1}t\right)\right]}^{k-2}$ ，

$o\left(t\right)$ 是关于t的高阶无穷小， ${\displaystyle \underset{k=0}{\overset{\infty }{\sum }}{A}_{1k}\left(t\right)}$ 一致收敛。

本文根据风险过程具有马尔科夫性，运用全概率公式与积分变换公式，得到该模型的期望红利现值函数满足的微–积分方程及特定分布下满足的微分方程与解析解，通过数值模拟和算例分析模型关键参数对期望红利现值函数的影响，得到一些有意义的经济见解，红利现值函数随初始资本、风险投资、固定保费收入、平均保费额的增大而增大，随偏离系数、平均索赔额的减小而减小，符合保险公司实际的经营状况。

3. 主要结果及证明

为了证明方便，记 $G^{*k}\left(y\right)$ 为 $G\left(y\right)$ 的k重卷积， $g^{*k}\left(y\right)$ 为 $g\left(y\right)$ 的k重卷积，并记：

$G_{{\rho }_1}\left(y\right)={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\left(1-{\rho }_1\right){\rho }_1^{k-1}}{G}^{*k}\left(y\right)$ ， $g_{{\rho }_1}\left(y\right)={\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\left(1-{\rho }_1\right){\rho }_1^{k-1}}{g}^{*k}(\; y\; )$

定理1当 $0\le u\le b$ 时，红利现值函数满足的微–积分方程为：

$\begin{array}{c}{V}^{\prime }\left(u;b\right)=\frac{{\lambda }^{\ast }+{\lambda }_1+\delta }{c+Fj}V\left(u;b\right)-\frac{{\lambda }^{\ast }}{c+Fj}{\displaystyle {\int }_0^{b-u}V\left(u+x;b\right)\text{d}F\left(x\right)}-\frac{{\lambda }^{\ast }}{c+Fj}V\left(b;b\right)\bar{F}\left(b-u\right)\\ -\frac{{\lambda }^{\ast }}{c+Fj}{\displaystyle {\int }_{b-u}^{\infty }\left[u+x-b\right)\text{d}F\left(x\right)}-\frac{{\lambda }_1}{c+Fj}{\displaystyle {\int }_0^{u}V\left(u-y;b\right)g_{{\rho }_1}\left(y\right)\text{d}y}\end{array}$ (3)

证明：时间 $dt$ 足够小时，结合引理2，在时间段 $\left(0,dt\right]$ 内有下面4种情况：

当随机保费收取，索赔发生次数均为0次时，概率为：

$\begin{array}{c}\mathrm{Pr}\left[M\left(dt\right)=0,N_1\left(dt\right)=0\right]=\left[1-{\lambda }^{\ast }dt+o\left(dt\right)\right]\left[1-{\lambda }_{1}dt+o\left(dt\right)\right]\\ =1-\left({\lambda }^{\ast }+{\lambda }_1\right)dt+o(\; d\; t\; )\end{array}$

2) 当随机保费收取0次，索赔发生 $k\left(\ge 1\right)$ 次，概率为：

$\begin{array}{c}\mathrm{Pr}\left[M\left(dt\right)=0,N_1\left(dt\right)=k\right]=\left[1-{\lambda }^{\ast }dt+o\left(dt\right)\right]\left[{\alpha }_1{\rho }_1^{k}dt+A_{1k}\left(dt\right)o\left(dt\right)\left(dt\right)\right]\\ ={\alpha }_1{\rho }_1^{k}dt+A_{1k}\left(dt\right)o(\; d\; t\; )\end{array}$

3) 当随机保费收取1次，索赔发生次数均为0次时，概率为：

$\mathrm{Pr}\left[M\left(dt\right)=1,N_1\left(dt\right)=0\right]={\lambda }^{\ast }dt\left[1-{\lambda }_{1}dt+o\left(dt\right)\right]={\lambda }^{\ast }dt+o(\; d\; t\; )$

4) 其他情况发生的概率为 $o(\; d\; t\; )$

对于上述情况2)，在时间段 $\left(0,dt\right]$ 内，总索赔量 $y>u+cdt+Fjdt+aW\left(dt\right)$ 时，破产一定会发生，此时不支付红利，因此由全期望公式及盈余过程具有马氏性得：

$\begin{array}{c}V\left(u;b\right)=E\left[V\left(U\left(t\right);b\right)\right]\\ =\left[1-\left({\lambda }^{*}+{\lambda }_1\right)dt+o\left(dt\right)\right]{\text{e}}^{-\delta dt}E\left[V\left(u+cdt+F\left(jdt+\sigma W\left(dt\right)\right);b\right)\right]\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]{\text{e}}^{-\delta dt}E\left[V\left(u+cdt+F\left(jdt+\sigma W\left(dt\right)\right)+X;b\right)\right]\\ +{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\left[{\alpha }_1{\rho }_1^{k}dt+A_{1k}\left(dt\right)o\left(dt\right)\right]{\text{e}}^{-\delta dt}E\left[V\left(u+cdt+F\left(jdt+\sigma W\left(dt\right)\right)-Y;b\right)\right]}+o(\; d\; t\; )\end{array}$

即

$\begin{array}{c}V\left(u;b\right)=\left[1-\left({\lambda }^{\ast }+{\lambda }_1+\delta \right)dt+o\left(dt\right)\right]V\left(u+\upsilon ;b\right)\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]{\text{e}}^{-\delta dt}{\displaystyle {\int }_0^{b-u-\upsilon }V\left(u+\upsilon +x;b\right)\text{d}F\left(x\right)}\\ +V\left(b;b\right)\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]{\text{e}}^{-\delta dt}\bar{F}\left(b-u-\upsilon \right)\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]{\text{e}}^{-\delta dt}{\displaystyle {\int }_{b-u-\upsilon }^{\infty }\left(u+\upsilon +x-b\right)\text{d}F\left(x\right)}\\ +{\text{e}}^{-\delta dt}{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\left[{\alpha }_1{\rho }_1^{k}dt+A_{1k}\left(dt\right)o\left(dt\right)\right]{\displaystyle {\int }_0^{u+\upsilon }V\left(u+\upsilon -y;b\right)\text{d}{G}^{*k}\left(y\right)}}+o\left(dt\right)\end{array}$ (4)

其中 $\upsilon =cdt+F\left(jdt+\sigma W\left(dt\right)\right)$ ， $\bar{F}\left(x\right)=1-F\left(x\right)$ ， ${\text{e}}^{-\delta dt}\approx 1-\delta dt$ ， $W\left(0\right)=0$ ，对(4)式移项整理得

$\begin{array}{c}V\left(u;b\right)-V\left(u+\upsilon ;b\right)=-\left[\left({\lambda }^{\ast }+{\lambda }_1+\delta \right)dt+o\left(dt\right)\right]V\left(u+\upsilon ;b\right)\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]\left(1-\delta dt\right){\displaystyle {\int }_0^{b-u-\upsilon }V\left(u+\upsilon +x;b\right)\text{d}F\left(x\right)}\\ +V\left(b;b\right)\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]\left(1-\delta dt\right)\bar{F}\left(b-u-\upsilon \right)\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]\left(1-\delta dt\right){\displaystyle {\int }_{b-u-\upsilon }^{\infty }\left(u+\upsilon +x-b\right)\text{d}F\left(x\right)}\\ +\left(1-\delta dt\right){\displaystyle \underset{k=1}{\overset{\infty }{\sum }}\left[{\alpha }_1{\rho }_1^{k}dt+A_{1k}\left(dt\right)o\left(dt\right)\right]{\displaystyle {\int }_0^{u+\upsilon }V\left(u+\upsilon -y;b\right)\text{d}{G}^{*k}\left(y\right)}}+o(\; d\; t\; )\end{array}$

由引理2知 ${\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{\rho }_1^k{g}^{\ast k}}\left(y\right),{\displaystyle \underset{k=1}{\overset{\infty }{\sum }}{A}_{1k}\left(dt\right)g^{\ast k}\left(y\right)}$ 均一致收敛，所以由单调收敛定理得

$\begin{array}{c}V\left(u;b\right)-V\left(u+\upsilon ;b\right)=-\left[\left({\lambda }^{\ast }+{\lambda }_1+\delta \right)dt+o\left(dt\right)\right]V\left(u+\upsilon ;b\right)\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]\left(1-\delta dt\right){\displaystyle {\int }_0^{b-u-\upsilon }V\left(u+\upsilon +x;b\right)\text{d}F\left(x\right)}\\ +V\left(b;b\right)\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]\left(1-\delta dt\right)\bar{F}\left(b-u-\upsilon \right)\\ +\left[{\lambda }^{\ast }dt+o\left(dt\right)\right]\left(1-\delta dt\right){\displaystyle {\int }_{b-u-\upsilon }^{\infty }\left(u+\upsilon +x-b\right)\text{d}F\left(x\right)}\\ +{\lambda }_{1}dt\left(1-\delta dt\right){\displaystyle {\int }_0^{u+\upsilon }V\left(u+\upsilon -y;b\right)g_{{\rho }_1}\left(y\right)\text{d}y}+o\left(dt\right)\end{array}$ (5)

方程(5)两端同时除以 $\upsilon$ ，令 $dt\to 0$ 得

$\begin{array}{c}{V}^{\prime }\left(u;b\right)=\frac{{\lambda }^{\ast }+{\lambda }_1+\delta }{c+Fj}V\left(u;b\right)-\frac{{\lambda }^{\ast }}{c+Fj}{\displaystyle {\int }_0^{b-u}V\left(u+x;b\right)\text{d}F\left(x\right)}-\frac{{\lambda }^{\ast }}{c+Fj}V\left(b;b\right)\bar{F}\left(b-u\right)\\ -\frac{{\lambda }^{\ast }}{c+Fj}{\displaystyle {\int }_{b-u}^{\infty }\left(u+x-b\right)\text{d}F\left(x\right)}-\frac{{\lambda }_1}{c+Fj}{\displaystyle {\int }_0^{u}V\left(u-y;b\right)g_{{\rho }_1}\left(y\right)\text{d}y}\end{array}$

定理2 假设 $X_i$ 服从参数为 $\alpha$ 的指数分布， $Y_i$ 服从参数为 ${\beta }_1$ 的指数分布，则 $0\le u\le b$ 时，红利现值函数满足的微分方程为

$\begin{array}{l}\frac{\delta \alpha \left(1-{\rho }_1\right){\beta }_1}{c+Fj}V\left(u;b\right)+\left[\frac{\alpha \left({\lambda }_1+\delta \right)-\left(1-{\rho }_1\right){\beta }_1\left({\lambda }^{\ast }+\delta \right)}{c+Fj}-\left(1-{\rho }_1\right){\beta }_1\alpha \right]V^{\prime }\left(u;b\right)\\ +\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }^{\ast }+{\lambda }_1+\delta }{c+Fj}\right]V^{″}\left(u;b\right)+V^{‴}\left(u;b\right)=0\end{array}$

且满足边界条件 $V\left(0;b\right)=0,V^{\prime }\left(b;b\right)=1,V\left(u;\infty \right)=0$ 。

证明：详细的证明理论与方法可参见文献 [15]，这里只做简单的证明

因为 $f\left(x\right)=\alpha {\text{e}}^{-\alpha x}$ ， $g^{\ast k}\left(y\right)=\frac{{\beta }_1^k{y}^{k-1}}{\left(k-1\right)!}$ ， $g_{{\rho }_1}\left(y\right)=\left(1-{\rho }_1\right){\beta }_1{\text{e}}^{-\left(1-{\rho }_1\right){\beta }_{1}y}$ ， $E\left(X_i\right)=\frac{1}{\alpha }$ ， $E\left(Y_i\right)=\frac{1}{{\beta }_1}$

对(3)式两端同时求一阶、二阶导数得

$\begin{array}{c}{V}^{″}\left(u;b\right)=\frac{{\lambda }^{*}+{\lambda }_1+\delta }{c+Fj}{V}^{\prime }\left(u;b\right)+\frac{{\lambda }^{*}\alpha -{\lambda }_1\left(1-{\rho }_1\right){\beta }_1}{c+Fj}V\left(u;b\right)\\ -\frac{{\lambda }^{*}\alpha }{c+Fj}{\displaystyle {\int }_0^{b-u}V\left(u+x;b\right)\text{d}F\left(x\right)}+\frac{{\lambda }_1\left(1-{\rho }_1\right){\beta }_1}{c+Fj}{\displaystyle {\int }_0^{u}V\left(u-y;b\right)g_{{\rho }_1}\left(y\right)\text{d}y}\\ -\frac{{\lambda }^{*}\alpha }{c+Fj}V\left(b;b\right)\bar{F}\left(b-u\right)-\frac{{\lambda }^{\ast }}{c+Fj}\bar{F}\left(b-u\right)\end{array}$ (6)

$\begin{array}{c}{V}^{‴}\left(u;b\right)=\frac{{\lambda }^{*}+{\lambda }_1+\delta }{c+Fj}{V}^{″}\left(u;b\right)+\frac{{\lambda }^{*}\alpha -{\lambda }_1\left(1-{\rho }_1\right){\beta }_1}{c+Fj}{V}^{\prime }\left(u;b\right)\\ +\frac{{\lambda }^{*}{\alpha }^2-{\lambda }_1{\left(1-{\rho }_1\right)}^2{\beta }_1^2}{c+Fj}V\left(u;b\right)-\frac{{\lambda }^{*}{\alpha }^2}{c+Fj}{\displaystyle {\int }_0^{b-u}V\left(u+x;b\right)\text{d}F\left(x\right)}\\ +\frac{{\lambda }_1{\left(1-{\rho }_1\right)}^2{\beta }_1^2}{c+Fj}{\displaystyle {\int }_0^{u}V\left(u-y;b\right)g_{{\rho }_1}\left(y\right)\text{d}y}-\frac{{\lambda }^{*}{\alpha }^2}{c+Fj}V(b;b)\bar{F}\left(b-u\right)\\ -\frac{{\lambda }^{\ast }\alpha }{c+Fj}\bar{F}\left(b-u\right)\end{array}$ (7)

${\displaystyle {\int }_{b-u}^{\infty }\left(u+x-b\right)\text{d}F\left(x\right)}=\frac{1}{\alpha }{\text{e}}^{-\alpha \left(b-u\right)}$ (8)

联立(3)式及(6)~(8)式可得

$\begin{array}{l}\frac{\delta \alpha \left(1-{\rho }_1\right){\beta }_1}{c+Fj}V\left(u;b\right)+\left[\frac{\alpha \left({\lambda }_1+\delta \right)-\left(1-{\rho }_1\right){\beta }_1\left({\lambda }^{\ast }+\delta \right)}{c+Fj}-\left(1-{\rho }_1\right){\beta }_1\alpha \right]V^{\prime }\left(u;b\right)\\ +\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }^{\ast }+{\lambda }_1+\delta }{c+Fj}\right]V^{″}\left(u;b\right)+V^{‴}\left(u;b\right)=0\end{array}$ (9)

边界条件为

$V\left(0;b\right)=0,V^{\prime }\left(b;b\right)=1,V\left(u;+\infty \right)=0$ (10)

对于方程(9)式的通解可设为

$V\left(u;b\right)=C_1{\text{e}}^{r_{1}u}+C_2{\text{e}}^{r_{2}u}+C_3{\text{e}}^{r_{3}u},0\le u\le b$ (11)

其中 $r_1,r_2,r_3$ 是方程

$\begin{array}{l}\frac{\delta \alpha \left(1-{\rho }_1\right){\beta }_1}{c+Fj}+\left[\frac{\alpha \left({\lambda }_1+\delta \right)-\left(1-{\rho }_1\right){\beta }_1\left({\lambda }^{\ast }+\delta \right)}{c+Fj}-\left(1-{\rho }_1\right){\beta }_1\alpha \right]r\\ +\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }^{\ast }+{\lambda }_1+\delta }{c+Fj}\right]r^2+r^3=0\end{array}$

的根。

根据边界条件可知

$C_1+C_2+C_3=0$ ， $C_1{r}_1{\text{e}}^{r_{1}b}+C_2{r}_2{\text{e}}^{r_{2}b}+C_3{r}_3{\text{e}}^{r_{3}b}=1$ ，

把(11)代入(3)并联立可解得 $C_1,C_2,C_3$ 的值，此时可解得红利现值函数的解析解。下面给出一种特殊的解析式，当 $\delta =0$ 时，记红利现值函数为 $\hat{V}\left(u;b\right)$ ，且容易得到 $\hat{V}\left(u;b\right)$ 的解析解。

推论当 $\delta =0$ 时，记红利现值函数为

$\hat{V}\left(u;b\right)=\frac{1}{r_1{\text{e}}^{r_{1}b}-r_2{\text{e}}^{r_{2}b}}{\text{e}}^{r_{1}u}+\frac{1}{r_2{\text{e}}^{r_{2}b}-r_1{\text{e}}^{r_{1}b}}{\text{e}}^{r_{2}u}$ (12)

其中

$\Delta ={\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }_1+{\lambda }^{\ast }}{c+Fj}\right]}^2-4\left[\frac{{\lambda }^{\ast }\alpha -{\lambda }_1\left(1-{\rho }_1\right){\beta }_1}{c+Fj}-\alpha \left(1-{\rho }_1\right){\beta }_1\right]$

$r_1=\frac{-\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }_1+{\lambda }^{*}}{c+Fj}\right]-\sqrt{\Delta }}{2}$ ， $r_2=\frac{-\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }_1+{\lambda }^{\ast }}{c+Fj}\right]+\sqrt{\Delta }}{2}$

证明：当 $\delta =0$ 时，方程(9)为

$\left[\frac{\alpha {\lambda }_1-\left(1-{\rho }_1\right){\beta }_1{\lambda }^{\ast }}{c+Fj}-\left(1-{\rho }_1\right){\beta }_1\alpha \right]{\hat{V}}^{\prime }\left(u;b\right)+\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }^{\ast }+{\lambda }_1}{c+Fj}\right]{\hat{V}}^{″}\left(u;b\right)+{\hat{V}}^{‴}\left(u;b\right)=0$ (13)

其中边界条件为

$\hat{V}\left(0;b\right)=0,{\hat{V}}^{\prime }\left(b;b\right)=1,\hat{V}\left(u;\infty \right)=0$ (14)

(13)式特征方程为

$\left[\frac{\alpha {\lambda }_1-\left(1-{\rho }_1\right){\beta }_1{\lambda }^{\ast }}{c+Fj}-\left(1-{\rho }_1\right){\beta }_1\alpha \right]r+\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }^{\ast }+{\lambda }_1}{c+Fj}\right]r^2+r^3=0$ (15)

$\Delta ={\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }_1+{\lambda }^{\ast }}{c+Fj}\right]}^2-4\left[\frac{{\lambda }^{\ast }\alpha -{\lambda }_1\left(1-{\rho }_1\right){\beta }_1}{c+Fj}-\alpha \left(1-{\rho }_1\right){\beta }_1\right]$

方程(15)的根为

$r_1=\frac{-\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }_1+{\lambda }^{*}}{c+Fj}\right]-\sqrt{\Delta }}{2}$ ， $r_2=\frac{-\left[\left(1-{\rho }_1\right){\beta }_1-\alpha -\frac{{\lambda }_1+{\lambda }^{\ast }}{c+Fj}\right]+\sqrt{\Delta }}{2}$ ， $r_3=0$

对于方程(13)式的通解可设为

$\hat{V}\left(u;b\right)=C_1{\text{e}}^{r_{1}u}+C_2{\text{e}}^{r_{2}u}+C_3,0\le u\le b$

根据边界条件(14)可知

$C_1+C_2+C_3=0$ ， $C_1{r}_1{\text{e}}^{r_{1}b}+C_2{r}_2{\text{e}}^{r_{2}b}=1$ ， $C_3=0$

解得

$C_1=\frac{1}{r_1{\text{e}}^{r_{1}u}-r_2{\text{e}}^{r_{2}u}}$ ， $C_2=\frac{1}{r_2{\text{e}}^{r_{2}u}-r_1{\text{e}}^{r_{1}u}}$

$\hat{V}\left(u;b\right)=\frac{1}{r_1{\text{e}}^{r_{1}b}-r_2{\text{e}}^{r_{2}b}}{\text{e}}^{r_{1}u}+\frac{1}{r_2{\text{e}}^{r_{2}b}-r_1{\text{e}}^{r_{1}b}}{\text{e}}^{r_{2}u}$

4. 数值实验

假设随机保费收入与索赔服从指数分布，利用数学软件，通过下列数值实验分析验证模型关键参数对函数(12)红利现值函数的影响，从而进一步验证文章结果的合理性，给保险公司提供指导性建议。

算例1在(12)式中设 ${\lambda }^{\ast }=0.01,\alpha =0.01,{\lambda }_1=0.001,{\beta }_1=0.1,F=10,j=0.15,b=60,c=10$ ，利用数学软件得到红利现值函数与初始资本、偏离系数的关系，如图1所示。且由图1可以看出红利现值函数是初始资本的增函数，因为初始资本越多，盈余就越多，得到的分红就越多。其次，红利现值函数是偏离系数的减函数，因为偏离系数越大，平均索赔就越大，盈余就越小，因此分红就会减小。

算例2在(12)式中， $u=50,{\lambda }^{\ast }=0.01,\alpha =0.01,{\lambda }_1=0.001,{\beta }_1=0.1,j=0.1,{\rho }_1=0.15,b=40,c=10$ ，利用数学软件得到红利现值函数与固定保费收入、风险投资额的关系，如图2所示。由图2可以看出红利现值函数是固定保费收入的增函数，因为固定保费收入越多，盈余就越多，得到的分红就越多。其次，红利现值函数是风险投资资产的增函数，因为风险投资越大，盈余就越大，因此分红就会变大。

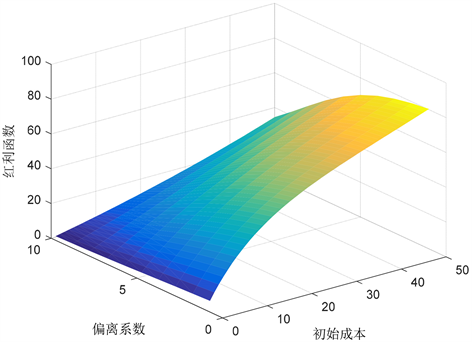
Figure 1. The influence of initial capital and deviation coefficient on the cumulative dividends present value function

图1. 初始资本和偏离系数对红利现值函数的影响

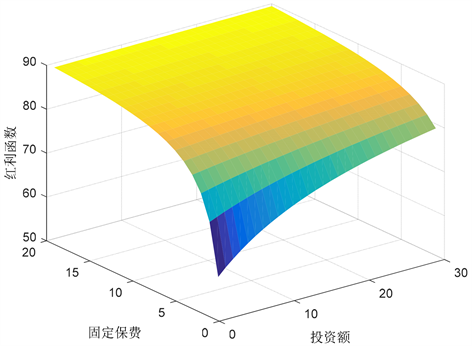
Figure 2. The influence of mixed premium income and risk investment on the cumulative dividends present value function

图2. 固定保费收入和风险投资额对红利现值函数的影响

算例3在(12)式中 $u=50,{\lambda }^{\ast }=0.01,{\lambda }_1=0.001,F=10,{\rho }_1=0.15,b=40,c=10,j=0.15$ ，利用数学软件得到红利现值函数与平均保费额、平均索赔额的关系，如图3所示。由图3可以看出红利现值函数是平均保费额的增函数，因为平均保费额越多，盈余就越多，得到的分红就越多。其次，红利现值函数是平均索赔额的减函数，因为索赔额越大，盈余就越小，因此分红就会变小。

Figure 3. The influence of premium income and claim numbers on the cumulative dividends present value function

图3. 保费额和索赔额对红利现值函数的影响

5. 结语

本文建立保费收取为固定保费和随机保费的带有风险投资收益的复合Poisson-Geometric风险模型，固定保费是服从线性增长过程，随机保费是服从复合Poisson过程，索赔过程是服从复合Poisson-Geometric计数过程。利用全概率公式与积分变换公式，研究该模型的期望红利现值函数满足的微–积分方程及特定分布下满足的微分方程与解析解，通过数值模拟和算例分析偏离系数、初始资本、风险投资、固定保费收入、平均保费额和索赔额对期望红利现值函数的影响，得出红利现值函数是关于初始资本、风险投资、固定保费收入、平均保费额的增函数，是关于偏离系数、平均索赔额的减函数，验证了文章结果的合理性。

本研究讨论的模型只考虑了风险资产的投资，没有考虑到无风险资产的投资，同时由于篇幅有限，也没有研究该模型其他精算量，如折现罚金函数、破产概率、破产前盈余分布函数、破产赤字分布函数等，今后我们将在风险资产投资的基础上充分考虑无风险资产投资，进一步研究Gerber-Shiu函数等。

基金项目

国家自然科学基金项目(11801105)；广西高校中青年教师科研基础能力提升项目(2021KY0767)——保险精算中保险风险模型破产概率计算与算法研究；广西民族师范学院科研经费资助项目(2021YB054)；广西民族师范学院科研经费资助项目(2020FG003)。

NOTES

^*通讯作者。