1. 引言
浅水波方程是对各种环境流体运动的数学描述,源项是底部地形。它对海洋,河流等波动问题的研究具有重要意义。带有源项的浅水波方程具有如下形式:
(1)
其中
h表示水深,u表示水流速度,g表示重力加速度,
表示底部地势,是关于x的函数。
当源项为0时,浅水波方程可以归结为双曲守恒律方程。即便双曲守恒律方程的初值函数是光滑的,它的解也可能会产生激波、接触间断等,这种情况的出现是不符合古典解有关理论的。为解决该类问题,1954年,Lax提出了弱解 [1] 这一概念,为数值方法的发展打下了良好的理论基础。Lax在1973年证明了熵稳定条件等价于“粘性消失” [2]。文献 [3] 把熵稳定条件引入到了带源项的浅水波方程。1987年Tadmor提出了熵变量和熵势的概念,构造了二阶精度的熵守恒格式,可以适用于各种网格 [4]。在熵守恒格式的基础上适当地加入一些粘性,就可以达到熵稳定。2006年,Roe提出在熵守恒格式上增加一个数值粘性项,称为ERoe格式,这是一类熵稳定格式 [5],该格式保持了Roe格式中,对激波的捕捉效果较好这一特点。熵守恒和熵稳定格式是获得具有物理意义的,且数值上稳定的解的一种高效途径,具有更实用的指导意义。2009年,Roe和Ismail进一步分析得到:当解在跨过激波时,会产生激波强度的立方量级熵增,在这基础上继续发展了求解Burgers方程与Euler方程时,将数值粘性项发展为更精准量化的熵相容格式 [6]。熵相容格式对数值粘性的控制比熵稳定格式的数值粘性更为精细,其数值结果更加符合物理现象,保证了激波稳定性的同时能得到更加精确的数值解。2018年,张海军,封建湖等构造了带源项的浅水波方程的熵稳定格式,模拟效果较好 [7]。2021年,任璇,封建湖等,提出了一种基于MUSCL重构的斜率限制器,有效地提高了双曲方程熵相容格式的分辨率 [8]。
本文采用有限体积法对带源项的浅水波方程求解,对源项使用中心差分格式离散,在熵相容格式的基础上,使用基于MUSCL重构的斜率限制器,对方程求解。通过数值实验证明该格式具有良好的性质,有效地避免了产生伪振荡等非物理现象。
2. 有限体积法
对式(1)在
上积分,得到半离散格式
(2)
其中
是
上的单元平均,
是数值通量,
是地势的中心差分。
定义
时间上采用使用三阶Runge-Kutta时间离散
(3)
其中
。
3. 带源项浅水波方程的求解
3.1. 熵相容格式
令熵函数为
,熵通量函数
,定义熵变量
,熵势
,从而可得熵守恒格式的数值通量
(4)
双曲守恒律方程的解在光滑处才是守恒的,根据熵条件
(5)
在激波等不连续点附近需要产生耗散,因此,需要额外添加耗散项,构建熵稳定格式。将熵变量的数值耗散项添加到熵守恒格式的数值通量,有
(6)
其中
是对称半正定矩阵。
Roe格式的数值通量具有如下形式 [6]
(7)
其中
是通量雅可比矩阵
的特征向量,
是以通量雅可比矩阵的特征值为对角线元素的非负对角矩阵。这些矩阵和特征值都是Roe平均状态。
因为
,其中
是对称正定的。由Barth特征向量缩放定理 [9],有
,Roe通量改写为
(8)
于是使用Roe的数值耗散项
(9)
为了简便,下文将
写为
。
带源项的浅水波方程有
(10)
(11)
Roe和Ismail指出,解在跨越激波时会产生立方级的熵增 [6],因此,需要更多的耗散项修正熵守恒格式,从而抑制振荡。
在二维双曲守恒律方程中,跨越激波产生熵增为 [6]
(12)
选择积分路径为
,
。熵增总是正的,即有
。
熵增
有
(13)
为了保证(13)的符号性,只需保证积分项正定,因此,作如下修正:
(14)
对应耗散项为
(15)
对上式的积分项使用Gauss-Legendre求积公式近似,于是有
(16)
其中
为求积系数,
为高斯点,在
上积分。本文中采用三点求积公式,高斯点和求积系数分别为
,
。因此,熵相容格式的数值通量为
(17)
3.2. 基于MUSCL格式的斜率限制器
在每个控制体单元
上,单元长度为
,对每个
进行重构,记重构后的函数为
,如果有
(18)
则称这个重构函数具有k-阶精度。
表示在第n个时间层上,控制体单元
的平均,有
(19)
于是有,
(20)
其中
是选择的重构斜率。于是,点
处的左右状态分别为
(21)
构造时,首先将重构函数
进行泰勒展开,有
(22)
继续将
在
处进行泰勒展开,可得
(23)
于是
(24)
将(24)带入(22),可得
(25)
取
(26)
重构函数是二阶的,即
。
记
(27)
其中
(28)
将一阶偏导和二阶偏导使用中心差商格式近似
将重构函数(27)增加斜率限制器,进一步提高精度,
(29)
其中
为增加的斜率限制器 [8]。
带有斜率限制器的重构在点
的左右状态,分别为
(30)
令
(31)
以确保不产生新局部极值,将(31)减去
得
(32)
当
,
时,有
(33)
即
(34)
因此,选择限制器
(35)
为了限制
,增加限制条件
(36)
于是,重构后的左右状态分别为
(37)
3.3. 高分辨率熵相容格式
将3.2节中的斜率限制器应用到带源项的浅水波方程,得到了具有带源项浅水波方程的二阶精度的高分辨率熵相容格式。
带源项的浅水波方程高分辨率熵相容格式的数值通量为
(38)
其中
是使用斜率限制器重构后的变量值。利用(37)式计算重构,
代替左状态
,
代替右状态
,根据重构后的
值得到熵变量
,最后将重构值带入(38),得到带源项浅水波方程的具有二阶精度的熵相容格式数值通量。
4. 数值实验
算例中的参考解使用2000个加密网格的熵稳定格式。EC表示熵相容格式,EC-Limited表示使用斜率限制器的高分辨率熵相容格式。
算例1. 考虑在区间
上,连续的底部地势
上的大型溃坝问题,初值条件为
取100个网格点,计算到
,取
,
,使用Neumann边界条件,图1所示,高度h的变化情况,熵相容格式的抹平现象更严重,带有斜率限制器的熵相容格式激波捕捉效果更好。
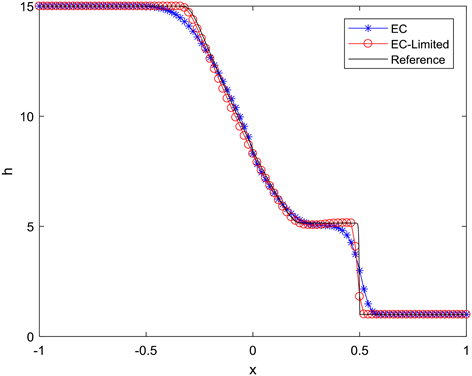
Figure 1. Variation of height h of large dam break problem
图1. 大型溃坝问题高度h的变化情况
算例2. 在
上计算溃坝问题,底部地势和初值条件分别为
取200个网格点,计算到
,取
,
,使用Neumann边界条件,图2所示是
的变化情况,熵相容格式有轻微的抹平现象,使用斜率限制器的熵相容格式效果更好,在捕捉到激波的情况下,抑制了伪振荡的产生。
算例3. 考虑在
上二维圆形溃坝问题,初值条件为
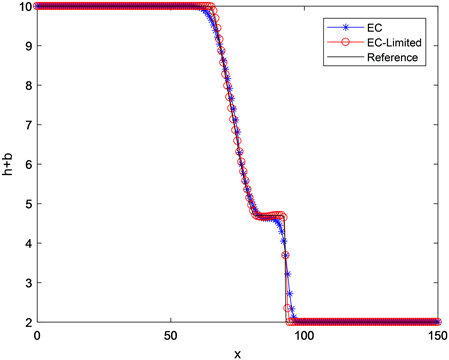
Figure 2. Variation of the total height
of the one-dimensional dam break problem
图2. 一维溃坝问题总高度
的变化情况
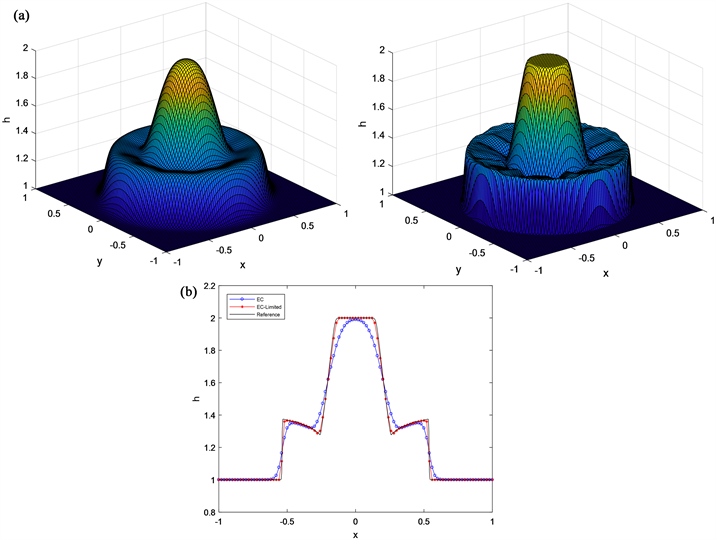
Figure 3. Variation of height h of two-dimensional circular dam break problem. (a) 3D graphics of height h in entropy consistent scheme (left) and high-resolution entropy consistent scheme (right); (b) The cross section
and the change in height h
图3. 二维圆形溃坝问题高度h的变化情况。(a)熵相容格式(左)和高分辨率熵相容格式(右)高度h的三维图形;(b)截面
高度h的变化
将空间离散为100 × 100个网格点,取
,计算到
,使用Neumann边界条件,如图3所示分别为熵相容格式和带有斜率限制器的高分辨率熵相容格式的关于高度h的三维图形和
的截面,的变化,熵相容格式的抹平现象较严重,带有斜率限制器的熵相容格式改善了这一情况,并且没有伪振荡产生,模拟效果更好。
5. 结论
浅水波方程的研究在实际生活中具有重要意义,通过数值实验表明带有基于MUSCL重构的斜率限制器的熵相容格式在捕捉激波时具有较好的效果,且抹平现象较少,避免了伪振荡的产生。该格式明显优于熵相容格式。但本文未对多维情况进一步推导,多维情况还需要对限制器进行修正,对多个维度重构,得到其高分辨率的熵相容格式。
NOTES
*通讯作者。