1. 引言
“高教社杯”全国大学生数学建模竞赛 [1] 是中国工业与应用数学学会于1992年创办的一类面向全国大学生的竞赛,每年一届,是首批列入“高校学科竞赛排名榜”前19项重要竞赛之一。该项竞赛旨在培养学生运用数学理论知识和计算机技术解决实际问题的能力,也是培养学生创新能力、创业能力的最佳载体。随着竞赛的不断深入,截止到2021年,全国已有49,529个队伍参加这项竞赛,并且受益学生多达14万之众。
数学建模竞赛的重要组成部分是应用数学理论知识建立数学模型来解决实际问题的一种实践 [2],即数学建模。通常需要对实际问题进行抽象和假设,找出恰当的数学关系,然后运用数学系统的知识方法对数学问题进行求解,并对现实问题做出解释的完整过程。数学建模竞赛的赛题主要来源于生活、社会热点话题、时事、科学研究课题,内容涉及自然科学、经济金融、人口环境、生物医学、工程技术、能源发展、交通、环境、行业问题等多个领域,具有灵活性、开放性、时效性等诸多特点。数学理论知识的运用则主要包括基础数学、优化理论、微分方程理论、统计分析、系统理论、图论与网络等。随着信息时代的飞速发展,以物联网、大数据、机器学习及人工智能等课题相关的竞赛题目不断涌现,以数据为驱动的命题也成为数学建模竞赛中重要的组成和内容。其中一个在竞赛中出现频率较高的赛题类型就是基于数据对某类事物或对象进行预测或控制。例如2003年国赛C题对SARS传播问题的预测;2005年国赛A题对长江水质未来10年的预测;2010年国赛B题上海世博会影响力的预测;2020年国赛C题中小微企业的信贷决策等。
2. 数学建模中的预测
预测 [3] 是指人们利用已经掌握的知识和手段,预先推知和判断事物未来发展状况的一种活动。具体来说,就是人们根据事物过去发展变化的客观规律,根据事物的运动和变化规律,运用各种定性和定量的分析方法,对事物未来可能出现的趋势进行科学推测。在数学建模竞赛中,基于数据驱动的预测方法主要包括:灰色系统预测、微分方程模型、回归分析预测、时间序列预测、小波分析预测,马尔科夫预测、数据拟合、插值预测、神经网络预测等。每种方法适用环境不同、基本原理不同、得到的预测结果也不同,要具体问题具体分析,要掌握各种预测方法的使用条件和范围。随着数学建模赛事的逐渐展开,一些数模工作者对数学建模中的预测方法前期都有过相关的讨论与总结。其中,2006年,张贻民等归纳了微分方程模型、时间序列方法、灰色预测、BP神经网络几种预测方法的工作原理,并介绍了这几种预测方法的优缺点 [4]。2010年,朱峰介绍了趋势外推预测法、时间序列预测法、回归预测法和灰色模型预测法的不同以及相关的数学理论 [5]。2011年,何家莉从教学角度对数学建模中的预测方法如何进行讲解、如何进行操作进行了论述 [6]。近两年来,许多数模爱好者也在各大网站、网络平台 [7] [8] 对数学建模中的预测方法有过讨论,但不得不说的是,现有的这些工作基本上都是从各种预测模型的基本工作原理、优缺点等出发进行讨论的,还未有文献具体的使用相同的数据驱动结合仿真来体现各种预测模型的效果。
因此,本文将以某公司2019、2020、2021年三年内每个月实际销售数据作为数据驱动(共有4302个客户,每年12个数据),选择不同的预测方法对该公司未来一年的销售情况进行预测。通过对数学建模中经常使用的各类预测方法的探讨和比较,论述每种方法的功能与区别,以此为数学建模竞赛中预测方法的选择提供参考依据。销售数据的部分样本如表1所示。

Table 1. Sample data of sales in 2019~2021 year
表1. 2019~2021年销售数据样本示例
2.1. 数据拟合法
数据拟合法 [9] 又称曲线拟合法,俗称拉曲线,是一种把现有数据通过数学方法对应到一个连续函数曲线上的方法。为了求出这条逼近曲线,通常让数据点在离此曲线的上方或下方不远处波动,最后利用最小二乘法来使得波动偏差达到最小。拟合函数确定后即可利用这个函数进行未来的预测。数据拟合思想直接、简单、计算量小,拟合的结果中不要求逼近曲线严格通过所有的数据点。并且许多数学相关的编程软件库都有提供非常完善的接口或调用函数,可直接对已有的离散数据集进行快速拟合,得到拟合曲线的相关参数。适用于数据量不大、线性关系比较显著的离散数据,但对非线性关系数据,特别是高维的非线性数据效果不够理想。图1展示了基于拟合法利用一年已知数据以及利用三年已知数据得到的预测结果。
2.2. 插值法
在数学建模过程中,当已知离散数据样本比较少,不足以拟合出正确的逼近函数时,就可以在原有样本点之间采用插值法产生比较符合原数据集特征的新数据点,增加样本数量,从而达到帮助建立模型的作用。通常选用较为简单的拉格朗日插值法或B-样条插值法来完成插值操作。插值法 [9] 的过程和拟合相似,但不完全相同,两者都是产生多项式处理数据集,但拟合不一定要经过原有的数据点,只是保证偏差的函数值最小即可,而插值的过程产生的多项式要经过原有的数据点,根据这个多项式,实现“预测”插值点的函数值。插值法的优点是简单易懂,编程方便。缺点是当数据集非常大的时候会使多项式的次数也非常高,运算的复杂度也相应膨胀。基于插值法利用一年已知数据以及利用三年已知数据得到的预测结果见图2。
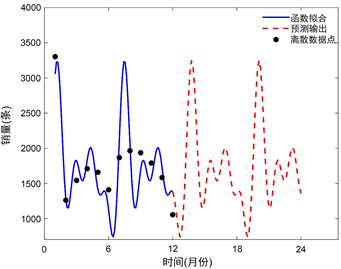
Figure 1. Prediction of sales derived from curve fitting method (left: with one-year sample data; right: with three-year sample data)
图1. 曲线拟合法销量预测图(左:用一年数据预测;右:用三年数据预测)
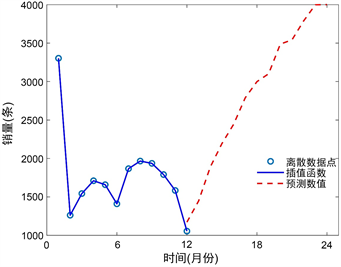
Figure 2. Prediction of sales derived from interpolation method (left: with one-year sample data; right: with three-year sample data)
图2. 插值法销量预测图(左:用一年数据预测;右:用三年数据预测)
2.3. 线性(或非线性)回归法
线性(或非线性)回归 [10] 是利用数理统计中回归分析思想,来确定两种或两种以上变量间相互依赖的定量关系的一种统计分析方法。与拟合和插值方法相比较,回归法不仅可以得到逼近数据点的函数表达式,也可以获知偏差的统计信息,比如偏差的均值与方差等。其优点是善于获取数据集中的线性或非线性关系,适用于在已有一些定义好的变量并且需要一个简单预测模型的情况下使用,训练速度和预测速度较快,在小数据集上表现很好,结果可解释,并且易于说明。缺点是可能会出现过拟合现象,分离原始数据和噪声的效果不够理想,并且在使用之前需要去除数据不相关的特征。基于多元线性回归法利用一年已知数据以及利用三年已知数据得到的预测结果见图3。
2.4. 神经网络法
神经网络是一种深度学习算法 [11],通过模仿生物神经网络的结构和功能来实现预测。神经网络的结构一般包含输入层、隐藏层和输出层。如图4所示,由大量的节点和之间的联接构成,每个节点代表一种特定的输出函数,称为激励函数。每两个节点间的联接都代表通过该连接信号的加权值,称之为权重,这相当于人工神经网络的记忆。网络的输出则因网络的连接方式、权重值和激励函数的不同而不同。神经网络模型可以根据结果的误差对模型进行修正,使得神经网络模型具有较好的容错能力,在局部或者部分神经元受到破坏后对全局的训练结果不会造成很大的影响。神经网络具有较强的非线性映射能力,具有实现任何复杂非线性映射的功能,但是达到理想效果的前提是对某些参数的调整是否合适,而调参的方法很大程度上依靠经验,对于神经元的数量和隐含层的层数的设置也是通过经验确定的。在数据量充足的情况下,神经网络是一种很好的拟合和预测方法,在设定训练集和测试集合的情况下具有不错的预测效果,但是由于神经网络模型类似黑箱,无法给出预测的合理解释,并且由于其可能存在的过拟合情况,需要预留足够的数据进行网络的检验。图5给出了基于长短期记忆网络(LSTM)结构的神经网络算法预测结果。
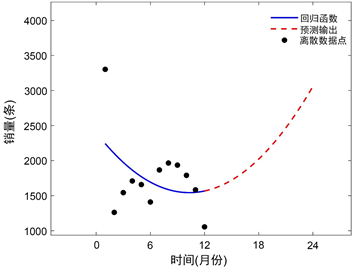
Figure 3. Prediction of sales derived from multiple linear regression method (left: with one-year sample data; right: with three-year sample data)
图3. 多元线性回归法销量预测图(左:用一年数据预测;右:用三年数据预测)
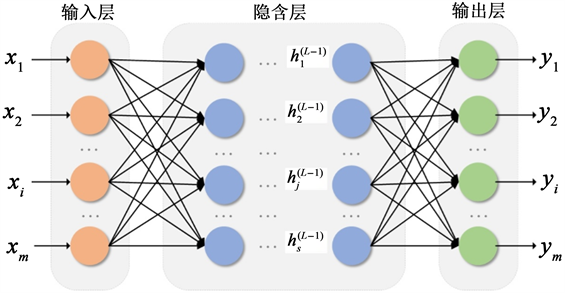
Figure 4. Schematic diagram of neural network structure
图4. 神经网络结构示意图
2.5. 时间序列法
时间序列法的主要功能是根据客观事物发展的连续规律性,运用过去的历史数据,通过统计分析,提取数据中数据蕴含的信息,进而将这种发展趋势延续到未来,预测未来可能产生的数据。优点在于可以从时间序列数据中找出变量变化的特征、趋势以及发展规律并将数据变化分解成趋势变化、季节变化、循环、随机变化等,从而对变量的未来变化进行有效地预测。常用的时间序列模型有自回归模型、滑动平均模型、自回归移动平均(ARIMA)模型等。其中ARIMA模型 [12] 是70年代初由Box和Jenkins提出的最全面的时间序列模型,能够实现前面提到的三种时间序列模型的所有功能,并能有效消除预测中的随机波动。比较而言,模型简单,只需要内生变量而不需要借助其他外生变量。其缺点是在使用已知数据进行预测前,必须对数据进行平稳性检验和白噪声检验,数据必须是稳定的,本质上只能捕捉线性关系,而不能捕捉非线性关系。基于ARIMA时间序列法的一年预测结果见图6。

Figure 5. Prediction by neural network
图5. 神经网络法销售预测图
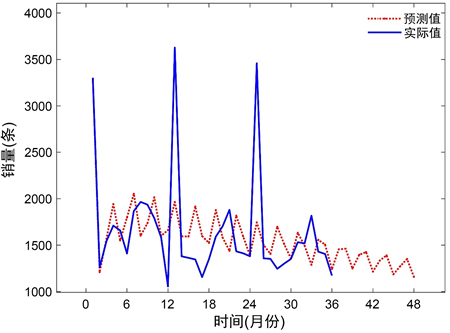
Figure 6. Future one-year sales prediction by ARIMA time series
图6. ARIMA时间序列法预测某客户未来一年销量
表2给出了本文采用的几种预测方法的误差结果。可以看出,相对于给定的三年销售数据,时间序列ARIMA模型的均方误差最小,使用36个月数据进行傅立叶拟合得到的平均绝对误差最小。说明时间序列模型和数据拟合方法比较适合本文给定的数据,预测效果相对较好。

Table 2. Error analysis and comparison of model
表2. 模型误差分析与比较
3. 结束语
数学建模竞赛中使用的预测方法并不局限于本文提到的这几种方法,还有其他几种常用的预测方法,例如微分方程模型,适用于基于客观规律和因果关系以及“变化相等”建立的关于变化率的模型。其优点是可以实现中、短、长期的预测,但缺点是由于方程的建立是以局部规律为基础,当作长期预测时误差较大,且多元的微分方程很难求解。代表性案例有传染病的传播预测、人口数预测、药物在体内的分布预测、烟雾的扩散与消失模型等。当历史数据较少、且完整性和可靠性较低时,可采用灰色预测模型。这种模型可以将无规律的原始数据进行累加生成近似的指数规律数据再进行建模与预测。其优点是适用于数据较少的情形,但只适用于中短期预测以及近似于指数增长的预测。另外还有马尔科夫模型、差分方程等也可以在一定条件下实现预测功能,要具体问题具体分析。总之,本文为参加数模竞赛的学生提供了预测方法的参考,在面对实际问题时,可针对数据不同的特点,选择最适合的、误差最小的模型进行预测。