弹性力学教学中若干问题的思考与讨论

Reflection and Discussion of Several Problems on the Teaching of Elasticity

摘要: 弹性力学是许多工程专业的必修课程之一，尽管弹性力学业已成为一门系统、完整且严密的学科，然而在弹性力学的教学中仍会遇到一些困惑与问题，这几个问题包括：圣维南原理的思考、一个练习题中出现的应力状态悖论、半无限体位移解答为何可用于两个球面体的接触问题以及应力强度与应变强度定义的说明。本文提出了作者的观点与看法，供讲授与学习弹性力学的师生们参考。

Abstract: Elasticity is one of the required courses for many engineering majors. Although elasticity has become a systematic, complete and rigorous discipline, there are still some puzzles and problems in the teaching of elasticity. The problems include 1) Reflections on Saint Venant’s principle; 2) The paradox of stress state in an exercise; 3) Why can the displacement solution of semi-infinite body be used to the contact problem of two spheres? 4) The definition of “stress intensity” and “strain intensity”. The ideas and views put forward in this paper can be used as a reference for teachers and students who teach and learn elasticity.

1. 关于圣维南原理的思考

圣维南原理从开始提出到现在已有一百多年历史 [1] [2]，在弹性力学中，人们利用它来放松边界条件使问题得到简化，解决了大量土木工程中的弹性力学边值间题。然而迄今人们对圣维南原理本身还存在着不少问题有待进一步研究，圣维南原理至今未得到完全的理论证明。

圣维南原理可以表述为 [3] [4]：若把作用在弹性体局部边界上的面力用另一组与它静力等效(主矢和主矩相同)的力系来代替，则在力系作用区域的附近，应力分布将有显著改变，但在远处所受的影响很小，可忽略不计。圣维南原理的另一种陈述是：如果弹性体局部边界上的面力是一个平衡力系(主矢及主矩都等于零)，那么这个平衡力系只会对其附近区域产生显著的应力，而对其远端产生的应力很小，可以忽略不计。

圣维南原理从直观上表现为弹性体内的应力在传递过程中具有趋向于发散、均匀的性质，例如：图1显示了梁端部的各种应力在传递过程中趋向于发散与均匀。

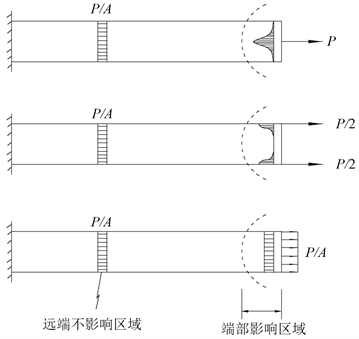
Figure 1. The stress at the end of the beam tends to diverge and be uniform during transmission

图1. 梁端部的应力在传递过程中趋向于发散与均匀

弹性体内应力的传递性质取决于弹性体内部的原子或分子之间力的传递机制，我们知道世界上存在四种力，它们分别为强力、弱力、引力与电磁力，强力与弱力为短程力，作用范围限于原子核内，而在微观领域内，引力的作用非常微小，因此只有原子或分子之间的电磁力支配了弹性体内的应力传递规律，即：弹性体内应力传递规律由微观电磁力学特性确定。作者认为(或猜测)，圣维南原理是一个由微观电磁力所支配的普遍性原理，在其它科学领域，如静电学、静磁学、传热学和流体力学领域也发现了圣维南原理 [1]，它们可能都源于相同的微观电磁力传递机制。

高桥邦弘 [5] 从宏观的层面，利用力的传递量和传递路线的概念导出了结构中力流的表达式，并通过力流的衰减来阐明圣维南原理。也有其他学者从弹性体变形能的角度 [2]，通过能量的衰减来证明圣维南原理。作者认为：圣维南原理证明的一种可能途径是，采用微观电磁理论，通过统计力学的方法，研究原子或分子之间的宏观应力传递特征，从而证明圣维南原理。

需要特别指出的是，弹性体内原子或分子之间电磁力的传递应基于原子或分子的完整性假设，即：原子或分子之间不出现断裂的现象，表现在宏观上，就是弹性体应具有连续的性质，这也是弹性力学的基本假设之一，因此弹性体的连续性假设是圣维南原理成立的基石，不应撇开连续性假设来讨论圣维南原理。

历史上，有一些学者提出了一些圣维南原理不适用的例子，其中一个典型的例子 [6] 是如图2所示的悬臂梁，端部作用一个平衡力系时，若在距离端部L的地方存在一个图示的裂缝，计算表明，无论L有多大，在裂缝尖端附近的应力都非常大，故对此例圣维南原理不成立。我们认为，由于裂缝的存在，破坏了弹性体的连续性(不符合弹性力学的基本假设)，在此种情况下讨论圣维南原理的适用性已毫无意义。其它的一些关于圣维南原理不适用的例子基本都有弹性体连续性受到阻断或阻碍的情形，从而使得圣维南原理不成立或不适用。

Figure 2. The crack destroys the continuity of the elastomer (resulting in the failure of the Saint-venant principle)

图2. 裂缝破坏了弹性体的连续性(导致圣维南原理不成立)

2. 一个练习题应力状态的悖论

几乎所有弹性力学教材中都采用了如图3的练习题：设有矩形截面的板(厚度为1)，容重为 $\gamma$，在其一个侧面上作用有均匀分布的剪力q，求应力分量。

仔细研究这一习题发现存在一个问题，取矩形板右上角点处的微体如图3所示，微体右边受均布剪力q ( $q\ne 0$ )，而微体上边没有外力作用，即 $\tau =0$，然而根据剪应力互等定理，应有： $q=\tau$，出现了图示加载与剪应力互等定理相互抵触的结果，图示的加载似乎没错，而剪应力互等定理更是不可动摇的力学法则。究其原因可以发现，图示加载在右上角点处不成立，即：在角点上，外部剪力q加不上去，或加上的剪力给卸载掉了(由于剪应力互等定理的支配)。

鉴于以上的问题，可将以上习题做适当修改：且设矩形截面上面受到剪切面荷载 $P_x$ 的作用，该面荷

载的分布不详，但其合力为零，即： ${\displaystyle {\int }_0^h{P}_x\text{d}x}=0$。

Figure 3. Stress paradox at the upper right corner

图3. 右上角点处的应力悖论

3. 为什么表面为平面的半无限体位移解答可用于两个球面体的接触问题？

两球体弹性接触问题是经典Hertz (赫兹)弹性接触理论中最基本的问题，在求解这一问题时，将半无限体表面受半球分布荷载作用下的位移解答直接作为球体的位移解答加以应用(见图4)，为什么表面为平面的半无限体解答可以用于两个球面体的接触问题，而且得到的解答与实测结果吻合良好。这一数学推导过程在现有的弹性力学教科书中被视为理所当然，然而对于许多初学者而言，这个数学推导比较难以接受，困惑不解，为什么将平面的结果直接用于球体，而不采用球体受荷载的结果？

Figure 4. The solution of the displacement of the semi-infinite body and the sphere

图4. 半无限体的位移解答直接作为球体的位移解答

这一问题涉及到相对尺度的概念，例如：当我们离开地球，以太空的尺度来观察地球时，发现地球是一个球体，当我们落在地球上时，以人体本身的尺度来观察地球时，发现地球是一个半无限体。对于两球体弹性接触问题而言，在外荷载作用下，由于弹性接触面非常微小，其接触面的半径远小于球体的半径，以接触面半径的尺度来观察球体时，球体的半径可以近似看成无限大，相当于我们站在地球上来观察地面，这时的球面就可以想象成半无限体的表面，这时就可直接引用半无限体表面受半球分布荷载作用下的位移解答，当然这个解答成立的必要条件是：接触面半径远小于球体半径，而实际两球体的弹性接触问题满足这一条件，因此得到的解答与试验结果很吻合。

对于球面受荷载的情形，当考虑受荷为球面时，将很难得到位移解答的公式解，也就无法得到两球体的弹性接触问题解答。

这种相对尺度的概念在其它学科里也会经常用到，例如：流体力学中流体在刚性平板表面边界层问题已经有相应的解答，当求解流体在刚性曲面上的边界层问题，常常采用平板表面边界层的解答，因为边界层的厚度与曲面的曲率半径相比要小很多，所以当以边界层厚度的尺度来观察曲面时，可以将曲面看成平面，因而就可以直接采用平板边界层的解答。

4. 关于“应力强度”与“应变强度”定义的澄清

现有许多弹性力学教科书将“应力强度”与“应变强度”分别定义为：

$\begin{array}{c}{\sigma }_i=\frac{1}{\sqrt{2}}\sqrt{{\left({\sigma }_x-{\sigma }_y\right)}^2+{\left({\sigma }_y-{\sigma }_z\right)}^2+{\left({\sigma }_z-{\sigma }_x\right)}^2+6\left({\tau }_{xy}^2+{\tau }_{xz}^2+{\tau }_{yz}^2\right)}\\ =\frac{1}{\sqrt{2}}\sqrt{{\left({\sigma }_1-{\sigma }_2\right)}^2+{\left({\sigma }_2-{\sigma }_3\right)}^2+{\left({\sigma }_3-{\sigma }_1\right)}^2}\left(主应力坐标下\right)\end{array}$ (1)

$\begin{array}{c}{\epsilon }_i=\frac{\sqrt{2}}{2\left(1+\nu \right)}\sqrt{{\left({\epsilon }_x-{\epsilon }_y\right)}^2+{\left({\epsilon }_y-{\epsilon }_z\right)}^2+{\left({\epsilon }_z-{\epsilon }_x\right)}^2+\frac{3}{2}\left({\gamma }_{xy}^2+{\gamma }_{yz}^2+{\gamma }_{xz}^2\right)}\\ =\frac{\sqrt{2}}{2\left(1+\nu \right)}\sqrt{{\left({\epsilon }_1-{\epsilon }_2\right)}^2+{\left({\epsilon }_2-{\epsilon }_3\right)}^2+{\left({\epsilon }_3-{\epsilon }_1\right)}^2}\left(主应变坐标下\right)\end{array}$ (2)

以上的定义或称呼与国际通用定义不一致，且容易与断裂力学中的应力强度因子相混淆，此外，当我们采用通用商业软件(如Ansys程序)进行应力与应变分析时，也容易产生混乱。国际通用定义是将上述(1) (2)式分别称为“等效应力(equivalent stress)”与“等效应变(equivalent strain)”，分别用 ${\sigma }_e$ 及 ${\epsilon }_e$ 表示。 ${\sigma }_e$ 也称为Von Mises应力，常常用于材料的强度计算或屈服状态的判定。而应力强度(stress intensity)则定义为：

${\sigma }_I=Max\left(\left|{\sigma }_1-{\sigma }_2\right|,\left|{\sigma }_2-{\sigma }_3\right|,\left|{\sigma }_3-{\sigma }_1\right|\right)\left(主应力坐标下\right)$ (3)

(3)式也称为Tresca应力。

5. 结语

本文讨论了弹性力学中的几个问题，结论归纳如下：1) 圣维南原理本质上体现了弹性体内应力的传递特征，应力的传递依赖于弹性体的连续性，圣维南原理应建立在连续性假设(弹性力学基本假设之一)上，撇开连续性假设来讨论圣维南原理无意义；2) 本文给出了一个练习题中应力状态出现悖论的原因；3) 本文用相对尺度的概念回答了为什么表面为平面的半无限体位移解答可用于两个球面体的接触问题；4) 本文澄清了当前“应力强度”与“应变强度”定义与国际通用定义的不一致性。