1. 研究背景
桥梁结构中悬索系统,斜拉索系统拉索的材料在选择上具有选择优异性,传统上选用钢索,但近年来,桥梁工程师们发现金属拉索在服役期间易腐蚀,而拉索在很高的张力水平下,轻微的腐蚀面积也会在后续使用中极大地缩短拉索的服役寿命,带来的维护成本更是惊人,据研究,全世界每年因金属腐蚀造成的直接经济损失约达7000亿美元,我国因金属腐蚀造成的损失占国民生产总值的4%,拉索的长期效能也备受行业和社会的关注。而碳纤维板用作索体材料比钢材更耐腐蚀,耐久性与抗疲劳性能优于钢索,可显著延长结构的耐久性,大幅度减少结构的维护费用。并且碳纤维拉索的预应力强度高,减振性能好,其优良的力学性能高性价比是未来传统钢索的潜在主力替代品。但是碳纤维板材料在长期受力过程中会产生蠕变和应力松弛,蠕变性能会削弱结构加固效果,进而影响结构正常工作,甚至会导致工程结构破坏从而造成巨大经济损失。与钢材相比,碳纤维板做索体主要具有如下几方面优点:1) 轻质高强:碳纤维板的密度仅为钢材的1/6,国产碳纤维板的抗拉强度 ≥ 2800 MPa,是钢筋抗拉强度的5倍以上,钢绞线的2倍;因此碳纤维能提供的预应力较之钢筋、钢绞线更大,其重量更轻;在未来的悬索桥结构中,碳纤维板有望作为轻质高强的结构件实现结构大跨度和轻量化 [1],碳纤维材料的本构关系为近似的线弹性关系,呈正比例直线,因此在张拉力在达到碳纤维极限强度前对其卸载,碳纤维材料都能完全恢复原状态,有利于实现结构自复位和可修复性 [2]。2) 耐久性:碳纤维板是各类纤维增强复合材料中在酸、碱、盐等各类环境耐腐蚀性能最佳的材料 [3]。如海洋环境、潮湿环境以及强酸强碱环境中,钢筋的耐久性表现远远不如碳纤维。经大量的试验研究,FRP材料在劣势环境中表现良好,与钢筋混凝土结构一般5年至15年会出现钢筋腐蚀 [4] 相比,碳纤维材料在海洋环境的耐久性表现更好,因此,研究人员在探索未来碳纤维材料运用于海上构造物的可能性,据预测利用碳纤维板建造的结构在海洋环境中的寿命可长达100年以上。3) 耐疲劳性能:碳纤维材料抗疲劳性能优秀。相同的疲劳应力比下,普通的HRB400钢筋在疲劳应力比为0.1,其疲劳应力幅限值为162 MPa [4],碳纤维板片材在应力幅约为2500 MPa下的最大疲劳应力限值为极限强度的83.7%,远高于普通钢筋的应力幅限值 [5]。碳纤维材料能经受疲劳强度为0.4抗拉强度的200万次循环,剩余强度达到90%以上。综合以上优点,碳纤维拉索前景可观,发展形势大好,其轻质高强,耐腐蚀的特性比钢绞线更能适应海洋环境,相信在不远的将来,碳纤维拉索系统将作为主体结构运用于悬索桥吊杆、斜拉桥的拉索中,彻底改变传统拉索行业。
2. CFRP拉索蠕变特性
2.1. CFRP材料的力学性能
CFRP材料是以树脂为基材,将具有高强度的碳素纤维作为增强体通过挤压,拉拔成型,形成具有轻质高强、耐腐蚀、抗拉强度高的复合材料。碳纤维增强聚合物片材(CFRP)作为一种新型材料,在结构工程领域作为加固材料,通过对构件施加预应力大幅度提升结构的抗弯承载能力,常用于桥梁的加固工程中。碳纤维材料不仅可作为加固材料,其质量轻于钢筋、钢绞线,其抗拉强度远高于钢筋,各类材料力学性能比较见表1,比钢材更耐潮湿、腐蚀,碳纤维板为索体材料时,碳纤维拉索的耐久性与抗疲劳性能优于钢索,可显著延长结构的耐久性,大幅度减少结构的维护费用;碳纤维拉索的预应力强度高,减振性能好可适用于斜拉桥、悬索桥类的桥梁结构中。预应力张拉后的CFRP拉索的抗拉强度,强度远远高于钢筋索缆,普通碳纤维板抗拉强度为1500~2500 MPa,而普通钢筋抗拉强度为490~700 MPa,钢绞线抗拉强度为1400~1860 MPa,碳纤维板的抗拉强度约为普通钢筋的3倍,钢绞线的1.2倍,除此以外,还有一种高强度碳纤维板,抗拉强度超过3000 MPa,约为普通钢筋抗拉强度的5倍,钢绞线抗拉强度的2倍以上。

Table 1. Comparison of mechanical properties between various fiber reinforcement and steel strand [6]
表1. 各类纤维筋与钢筋钢绞线力学性能对比 [6]
2.2. CFRP材料的蠕变机制
蠕变是材料受恒载作用下,变形随时间增加而增加的现象,碳纤维板材料保留了基体材料中树脂材料的部分特性,树脂材料为粘弹性材料,因此碳纤维材料也有蠕变特性。实际加固工程中,通过对碳纤维板表面涂抹一层环氧树脂胶,然后进行张拉并锚固于梁底,使碳纤维板和与梁体形成一个整体,再撤去张拉设备。在桥梁通行中,碳纤维与梁共同受力,车辆产生的可变荷载影响与结构共同受力的碳纤维材料应力状态,在可变荷载撤去后又能恢复到原定状态,但当可变荷载与恒定荷载的比例足够小时,即忽略可变荷载,整体受力看作恒定荷载。在预应力碳纤维板加固桥梁工程中,碳纤维板产生的蠕变可能导致结构出现下挠现象,它的蠕变阶段如图1所示。蠕变率是特定时刻的蠕变应变相对于初始应变的增长率,是作为衡量碳纤维材料的蠕变变形的重要指标。

Figure 1. Three stages of creep of fibrous materials
图1. 纤维材料蠕变三阶段
3. CFRP拉索蠕变理论
对于锚固系统下CFRPR蠕变性能研究,目前主要采用下面种力学方法进行分析,为经验方程和Maxwell模型、Kelvin模型。
3.1. 经验方程
通过大量的蠕变试验获得数据,并利用数学统计法,将试验数据进行回归分析或拟合成有规律的方法,并将最终拟合的曲线作为求解蠕变性能的方程,这种方程成为经验方程。根据蠕变理论,粘弹性材料的蠕变过程通常分为以下四个阶段:弹性阶段、瞬间蠕变阶段、等速蠕变阶段和加速蠕变阶段。蠕变的宏观表现形式即为这四个阶段微观应变的总和,因此,材料在长期荷载作用下的蠕变总量为下式:
式中:
——总蠕变量;
——初始弹性应变;
——瞬间蠕变;
——等速蠕变;
——加速蠕变;
参考碳纤维蠕变相关文献可发现,碳纤维材料为粘弹性材料,其常见的蠕变经验公式主要有指数函数、对数函数以及幂函数等,需要对整个系统受力的每一过程进行大量的数据采集。
3.2. 流变模型
流变模型的原理是由三类基本元件组成通过不同连接形式如串联、并联连接后,模拟受力时各元件的应力应变变化,从而分析整个模型的应力应变变化。通过用粘、弹、摩擦元件模拟材料受力时的微观分析,能更形象的模拟出材料的蠕变机理。分子内部间的变化,分子与分子间变化均可用粘、弹性元件进行模拟。采用元件组合方式模拟的模型能形象化的模拟出CFRP板材蠕变机理,有利于从机理上认识到蠕变的变形叠加效应,因而这类模型更能从本质上反应出CFRP的材料特性。弹性元件、塑性元件以及摩擦器作为组成元件本构模型的三类基本元件,可分别模拟材料的弹性、粘性和塑性特质。弹性元件:弹性元件图2(a)所示,可以用弹簧表示,此类元件的特点就是在施加荷载后产生变形,并在一定荷载时保持变形,变形随卸载逐步消失,并在荷载减至零时完全消失。此变形并不随时间变化,也不受温度和湿度的影响,只与荷载本身相关。因此,在弹性物体加载和卸载中,不消耗能量,将所做的功全部转换。弹性元件最大的特点就是变形可恢复;著名的胡克定律,就是弹性元件。
式中:k——弹簧刚度系数。
粘性元件:粘性元件图2(b)所示,阻尼器可看作是由油壶和活塞组成。
粘性元件的特点是在应力作用瞬间不会立即产生应变,应力增加过程中,应变也随时间增加,应力与应变在其他条件不变的情况下呈正相关性。应力与应变速率为正比关系
分别为粘滞系数和应变速率。塑性元件:塑性软件如图2(c)所示,塑性元件可以看作两个滑块之间接触摩擦,其变形特点为,当外加应力小于自身摩擦阻力时,不发生变形;当外应力超过摩擦阻力时,应力恒定的情况下发生塑性变形,初应力水平决定塑性变形,与时间无关。
 (a) 弹簧 (b) 阻尼器 (c) 摩擦器
(a) 弹簧 (b) 阻尼器 (c) 摩擦器
Figure 2. Basic elements of rheological model
图2. 流变模型基本元件
以上几种基本元件进行组合,可组成与我们试验相符合的流变基本模型。
3.2.1. Maxwell模型(串联模型)
如图3所示,Maxwell模型将弹性元件与粘性元件串联,此类模型可模拟液态材料的粘弹性。受力作用时,弹性元件和粘性元件收受应力相变,应变不同,因此,模型总应变为两元件应变之和 [7]。
该模型的流变方程为:
设弹簧的刚度系数为k,粘壶内的液体粘度为
,
为应变速率
Maxwell模型本构方程如下:
Maxwell模型能模拟出应力松弛过程,但不能模拟出聚合物的蠕变过程。
3.2.2. Kelvin模型(并联模型)
如图4所示,Kelvin模型由弹性元件和粘性元件并联而成,主要表示固态的粘弹性,弹性元件可模拟材料的骨架变形,粘性元件模拟填充空隙粘性物质的变形。在力的作用瞬间,开始为粘性元件受力变形,并逐渐将传力到弹性元件,宏观表现为填充物质发生变形后,荷载向弹性元件逐步转移,其分子宏观表现为骨架结构发生宏观变形。在受力后期,荷载全部转移到弹性元件,粘性元件仅仅在开始时作用,该并联模型中应变相等,总应力为两元件应力之和。
该模型的流变方程为:
Kelvin模型的本构方程如下:
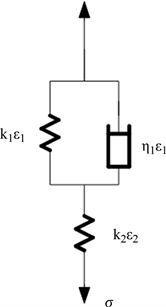
Figure 5. Kelvin standard linear solid model
图5. 开尔文标准线性固体模型
Kelvin模型能模拟出材料蠕变过程,但不能模拟出聚合物的应力松弛过程。
3.2.3. 标准线性固体模型
如图5所示,标准线性固体模型由一个Kelvin模型与一个弹簧元件串联而成的力学模型,称为开尔文标准线性固体模型,通常采用这类模型用来描述材料的蠕变现象,即假设应力不发生改变的情况下,应变与时间之间的关系 [8]。
首先引入弹簧柔度,柔度对应弹簧刚度k值,二者互为倒数关系。
模型并联部分的应变
,并联模型的应变相等,总应力为粘、弹两元件相加之和。
对以上公式作拉普拉斯变换
,
,
。
等式两边同乘
,令
,得
模型串联部分的弹簧应变
,经拉普拉斯变换后为
,模型总应变为串联部分与并联部分的应变之和
在蠕变试验中的材料应力保持常量,即始终为
,故有
将此值代入上式,并作拉普拉斯逆变换,则开尔文标准性固体模型的蠕变响应即为纯应变与时间的关系
为蠕变柔量,
即为与时间相关的应变变化公式。
标准线性固体模型经公式理论推导后,绘制出的蠕变柔量变化曲线与时间成对数函数关系,即为材料的蠕变柔量增速随时间变化逐渐趋缓。该模型作为理想化的模型,仅考虑应力不发生改变的情况下,应变与时间之间的关系,与本次碳纤维拉索系统中荷载恒定,应力不改变的情况相符,因此试验选用标准线性固体模型作为本次蠕变试验的预测模型,将本次的碳纤维拉索蠕变试验的时间–蠕变曲线是否符合标准线性固体模型的蠕变规律作为试验成功的标准。
4. 试验方案
1) CFRP板松弛加载装置设计
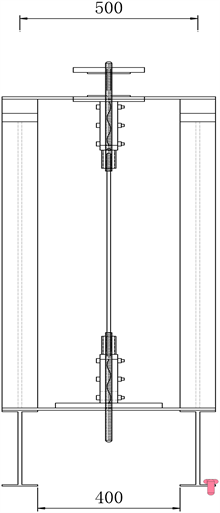
Figure 6. Front elevation of test frame
图6. 试验架正立面图
使用如图6、图7所示的加载装置施加荷载对CFRP板进行张拉,利用杠杆原理,力臂为长1700 mm的30工字钢,其右侧需要焊接挂钩,承重大约2吨。由竖向支撑间焊接放置14b槽钢和工字钢底部焊接角钢作为杠杆支点,通过在挂钩上悬挂混凝土试块来施加荷载,张拉弧形板,如图7所示。碳板的板宽面面向立面。碳板端距支点距离为250 mm,力臂间的比例为0.21,设置三个观测区域,分别是固定端碳板滑移量观测区(如图8所示),中间段碳板应变观测区,张拉端碳板滑移区。混凝土规格选用1225 kg、1837.5 kg和2450 kg。
2) 实验测量装置(应变片、百分表)

Figure 9. Carbon plate strain gauge adhesion
图9. 碳板应变片粘贴
在碳板上以碳板长度的1/8、1/4、1/2……处贴应变片,用以测量荷载和应变;粘贴位置见图9,将百分表置于固定端测量锚具的滑移,固定端示意图见图10。
3) 碳板设计
将碳板分组编号为1-40,1-60,1-80,截面尺寸均为50 × 1.2 mm,抗拉强度均为2460 MPa,张拉水平分别为40%、60%、80%,通过混凝土试块进行加载,加载重量分别为1230 kg、1837.5 kg、2450 kg,混凝土规格分别为0.9 × 0.9 × 0.5 m,0.9 × 0.9 × 0.75 m,0.9 × 0.9 × 1.0 m。
4) 数据收集
收集持载过程中的应变,位移数据,拟合成蠕变变化近似曲线(见图11),分析得出材料蠕变变化规律、锚具与碳纤维间相对滑移量规律。
5. 结论
通过对试验数据的多项式拟合,计算出蠕变模型的参数值,再重新计算碳纤维板的理论模型。经理论与试验分析对比,模拟碳纤维板采用的蠕变模型计算得出的蠕变变化与试验的蠕变变化趋势较为符合,但蠕变模型仅考虑的应力水平,而试验过程中周围环境会对碳板蠕变产生一定的影响,因此试验的蠕变量与理论蠕变量相比有一定的误差。经试验研究表明:应力水平不同的情况下,碳纤维持载时间–蠕变率曲线蠕变率趋势大致相同,均为先快后慢,并逐渐趋于稳定;锚具的抗滑移性良好,锚具可靠性高,三组数据中滑移最大值不超过碳纤维板总长度的0.01%;碳纤维拉索蠕变试验规律曲线符合标准线性固体模型的蠕变曲线规律,因此本实验有一定的工程参考价值。
基金项目
重庆科技学院硕士研究生创新计划项目(项目批准编号:YKJCX2120651)。