影响绿色债券利率的相关因素探究

Exploration on the Relevant Factors Affecting the Green Bond Interest Rate

摘要: 随着我国经济的快速增长，环境问题日益尖锐。究其根源在于我国经济增长是以高能耗为代价，致使环境问题日益严重，制约了我国经济的可持续发展。因此，本文决定开展有关绿色金融发展与相关各影响因素的分析。文章第一个模型选取了2016年至2022年5月发行的1842支绿色债券作为研究样本，获取相关债券的信用评级、发行时的票面利率，发行总额，发行年限、以及上市日期数据，通过使用Matlab以及Eviews软件建立多元线性回归模型。随后我们进行了VIF检验、异方差检验以及残差检验。经验证，得出以下结论：专项指引政策、债券评级等越高或越好，绿色债券发行利率越低。文章第二个模型针对时间序列模型，选择了1978~2021年共44年的全国每万元GDP的综合能耗作为研究样本来探究各因素对绿色金融的影响程度。首先对原始数据进行了平稳性检验，随后根据结果进行了二阶差分。然后开展了单位根以及白噪声检验，发现此模型较好通过了上述两个检验。接下来进行模型的构建，经过检验，认为此模型能较好拟合序列。于是我们对接下来3年中国的每万元GDP的综合能耗进行了预测，并给出了相应建议及结论。

Abstract: With the rapid growth of China’s economy, environmental problems have become increasingly acute. The root cause is that China’s economic growth is at the cost of high energy consumption, re-sulting in increasingly serious environmental problems, restricting the sustainable development of China’s economy. Therefore, this paper decided to carry out the analysis of the development of green finance and related influencing factors. The first model of this article selected 1,842 green bonds issued from 2016 to May 2022 as research samples to obtain the credit rating, coupon rate, total issuance amount, issuance date, and launch date data, by using Matlab and Eviews software a multiple linear regression model was developed. Subsequently, we performed the VIF test, the het-eroscedasticity test, and the residual test. It has been proved that the following conclusions are drawn: the higher or better the special guidance policy and bond rating, the lower the interest rate of green bond issuance. The second model in the paper aims at the time-series model. The national comprehensive energy consumption per 10,000 Yuan of GDP for 44 years from 1978 to 2021 was selected as the research sample to explore the influence of various factors on green finance. The original data were first tested for stationarity, followed by a second-order difference from the re-sults. Then the unit root and white noise test, found that the model is better after the above two tests. Next, the model is constructed, and after testing, the model can fit the sequence well. There-fore, we predicted the comprehensive energy consumption per 10,000 Yuan of GDP in China in the next three years, and gave the corresponding suggestions and conclusions.

1. 引言

2022年10月，中共二十大会议把“人与自然和谐共生的现代化”上升到“中国式现代化”的高度，使得新时代的中国生态文明建设进一步明确。在绿色低碳领域取得颇多成就的同时，也需要关注到我国生态环境结构性的压力暂未缓解，绿色金融发展的重要性更加不言而喻。在绿色发展的大背景下，研究绿色债券的影响因素就显得尤为重要，这不仅为绿色金融的发展提供了新的思路，也间接推动了绿色金融的创新，从而使得绿色债券市场良性发展。探究绿色金融对环境治理的影响也具有重要价值。

2. 文献综述

2.1. 理论分析

2.1.1. 市场利率化

一般而言，利率市场化就是指政府赋予金融市场确定利率的能力。利率市场化为全国金融界的一项重要机制，它的主要意义在于很好地配置了市场上的闲置资金，使市场机制在资源分配中发挥中心作用 [1]。

2.1.2. 可持续发展理论

可持续需求理论的基本含义是，在努力满足当代人类需要的同时，并不给后代人满足自身需求的努力造成损失的理论。可持续发展的观念在创新与改革的道路上不断深化，对绿色金融的研究也有着重要意义 [2]。

2.2. 前人研究

董晓红等(2018)使用碳排放量指标、地区生产总值、空气质量指数等解释变量,得出城市环境金融的发展水平与金融发达程度呈正相关性，以及与环境因素呈负相关，以及与金融发达程度呈正相关性的情况结论 [3]。方建国等(2019)通过以人均实际GDP、产业结构提升指标，以及煤炭消费量与能源消费总额之间的比例建立回归模式，并得到“经济、产业结构提升和提高能源水平程度均能促使绿色金融行业增长差距减小”的结果 [4]。

3. 数据来源

3.1. 数据来源与样本选择

3.1.1. 数据来源

选取2016年至2022年5月发行的1842支绿色债券作为研究样本，获取相关债券的信用评级、发行时的票面利率，发行总额，发行年限 [5]、以及上市日期。针对时间序列分析选择1978~2021年共44年的全国每万元GDP的综合能耗为研究样本。数据来源于国家统计局、中国债券信息网、中国货币网、上海证券交易所、深圳证券交易所、choice数据库、前瞻数据库和GJ统计局。

3.1.2. 样本选择

为避免异常值带来的影响，从总体数据中剔除较少的绿色熊猫债，绿色地方债以及信息较难获取的境内主体境外发行债，剔除缺少债项评级的债券，剔除缺少发行期限的债券，剔除未上市状况公司的债券，以保证数据的完整性和结果的可靠性。经过筛选，最终获得1205份有效债券样本数据，建立了相关线性回归模型的数据；获得1978~2021年共44年全国每万元GDP的综合能耗时间序列数据。

3.2. 变量定义与描述

3.2.1. 被解释变量

本文选取绿色债券发行的票面利率作为被解释变量。我国绿色债券本身是为了畅通绿色企业融资渠道，降低绿色企业融资成本，促进绿色企业发展而由政府由上至下引导发展的特殊债券，因此其票面利率相比于普通债券利率要更低才能起到期望的作用。但是由于绿色债券的一些特性的存在，其利率会受到一定程度的影响。而绿色债券能否真正表现出绿色企业通过发行绿色债券相比发行普通债券融资的优越性，能否展现出绿色债券的“质”，还是要对绿色债券的发行利率进行研究 [6]。

3.2.2. 解释变量

本文的解释变量由宏观因素和微观因素两部分组成。宏观因素包括专项政策指引状况，微观因素包括绿色债券的发行规模、发行期限以及债项评级。

专项政策指导状况

由于我国绿色债券市场是由国家政府以及相关机构自上而下引导发展，具有一定的政策性。发布的国家指导政策越多，绿色债券运行就越规范，绿色债券促进绿色产业相关企业融资的效果就越好。本文将选择绿色债券专项政策指导状况作为政策状况的指标，专项政策指导状况通过不同种类债券发行月份之前的相关指导政策的数量来表示。

债券发行规模

根据流动性偏好理论及债券期限理论，由于一般企业的偿债能力有限，若债券发行规模较大，其相应的偿债风险会增大，其偿债期限会延长，导致企业对于债务的偿债压力增强，偿债风险提高，从而债券的信用风险增大，最后会导致债券的利率上升。

债券发行期限

同样根据流动性偏好理论及债券期限理论，投资者在投资过程中更偏好流动性较高、风险较低但收益率较低的短期债券，期限越长的债券由于缺乏流动性以及利率风险较高，投资者需要的风险溢价也较高，因此其对应的收益率也高。

债券评级

债券评级反映了企业的财务状况、管理状况以及与债券相关的状况。根据ESG理念债券的评级还应包括与企业与债券相关的环境影响状况，体现了一定的绿色性。但目前ESG理念还未完善运用到我国债券评级机构的评级系统中，因此未将债券评级纳入绿色影响因素中，但随着社会不断的发展，债券评级中包含的绿色因素会越来越多。一般债券评级越高的债券，其相关信用风险越低，因此其债券发行利率一般会越低。

3.2.3. 控制变量

基准利率

在利率市场化的背景下，资金融资双方衡量收益以及国家管理层做经济决策都需要有一个公认的基准利率进行参考，而本文为了数据的统一与简洁，从而认为基准利率为定值，将其作为控制变量。

3.2.4. 变量定义表

变量定义表如下表1所示。

Table 1. Variable definition table

表1. 变量定义表

4. 绿色债券利率影响因素回归分析

4.1. 绿色债券利率的一般影响因素研究假设

1) 假设绿色债券发行利率与债务发行规模呈正相关关系。若债券发行规模较大，其相应的偿债风险会增大，其偿债期限会延长，导致企业对于债务的偿债压力增强，偿债风险提高，从而债券的信用风险增大，最后会导致债券的利率上升。

2) 假设绿色债券发行利率与债务发行期限呈正相关关系。根据流动性偏好理论及债券期限理论，投资者在投资过程中更偏好流动性较高、风险较低但收益率较低的短期债券，期限越长的债券由于缺乏流动性以及利率风险较高，投资者需要的风险溢价也较高，因此其对应的收益率也高。

3) 假设绿色债券利率与债券评级呈负相关关系。一般债券评级越高的债券，其相关信用风险越低，因此其债券发行利率一般会越低。

4) 假设绿色债券利率与其专项政策指导状况呈负相关关系。发布的国家指导政策越多，绿色债券运行就越规范，绿色债券促进绿色产业相关企业融资的效果就越好 [7]。

4.2. 数据预处理

如图1所示，首先对票面利率、发行规模、发行期限、债项评级和专项政策指引状况取自然对数，其目的在于去除负值对结果的影响同时减小量纲对结果的影响，使得二者关系在散点图中更加明显。使用Eviews分别作出散点图，我们可以发现债务发行规模、债务发行期限、债券评级以及专项政策指导状况皆与绿色债券发行利率呈负相关关系。绿色债券发行规模越大，绿色债券发行利率越低。这与我们之前建立的假设(1)不符。通过查阅资料可以发现，可能是绿色债券发行规模与发行期限等其他因素不稳定，或债券规模单位选择不合适。绿色债券的发行期限越长，绿色债券发行利率越低，也与假设(2)不符。原因可能是绿色债券市场发展时间较短，发行期限波动较大。绿色债券评级越高，绿色债券发行利率越低，与假设(3)相符，说明绿色债券评级可以反映绿色债券的风险状况，从而影响发行利率。专项指引政策的数量会影响绿色债券的发行利率，专项指引政策的数量越多，绿色债券发行利率越低，与假设(4)相符，说明了绿色债券的政策性。综上，我们认为上述数据点的存在基本合理，我们可以运用其对进行模型建立而不会产生较大影响。

Figure 1. Scatter plot

图1. 散点图

4.3. 共线性检验

首先选取上述变量定义表中的票面利率作为解释变量，发行规模、发行期限、债项评级和专项政策指引状况作为解释变量，基准利率作为控制变量。本章拟通过构建数据模型实证研究前文所提到的四种因素对绿色债券票面利率的影响，为了降低指标数据单位以及异方差的影响，变量均取自然对数 [8]。构建如下模型：

$\ln y=a_0+a_1\ln x_1+a_2\ln x_2+a_3\ln x_3+a_4\ln x_4+{\epsilon }_t$

其中 $\ln x_1$ 、 $\ln x_2$ 、 $\ln x_3$ 、 $\ln x_4$ 分别表示发行规模、发行期限、债项评级和专项政策指引状况的对数， $\ln y$ 表示绿色债券票面利率的对数值， ${\epsilon }_t$ 为残差项， $a_0$ 表示常数项。

对上述模型使用OLS最小二乘法进行拟合，根据VIF方差膨胀因子进行共线性检验，并得到相关系数矩阵与图形进行辅助判断，结果如下表2：

Table 2. VIF variance inflation factor test and correlation coefficient matrix

表2. VIF方差膨胀因子检验及相关系数矩阵

由上表的结果可以知道， $\ln x_1$ 、 $\ln x_2$ 、 $\ln x_3$ 、 $\ln x_4$ 、 $\ln y$ 的VIF值均小于10，同时参考相关系数矩阵可知，它们的相关系数较小，我们可以认为模型共线性较小，不会对后续的研究产生影响 [9]。因此，我们可以运用此模型进一步进行分析，模型如下：

$\ln y=2.046867-0.043814\ln x_1-0.013607\ln x_2-0.641505\ln x_3-0.109274\ln x_4$

4.4. 残差检验

首先作模型的残差图以及正态QQ图观察样本残差分布是否符合正态分布。

从残差图以及正态QQ图(图2、图3)中我们可以观察到样本残差基本服从正态分布，这符合我们OLS最小二乘法的基本假设。下面从偏度、峰度以及D.W.检验定量确定残差是否服从正态分布。

Figure 2. Residual plot

图2. 残差图

Figure 3. Normal QQ plot

图3. 正态QQ图

由表3我们可以知道样本残差的偏度较小、峰度接近3，这符合正态分布的要求。同时D.W.检验值接近2，p值为0.468大于0.05，残差不存在序列相关性，接受原假设即可以认为残差服从正态分布，样本数据通过残差检验。

Table 3. Skewness, kurtosis, D.W. test related results

表3. 偏度、峰度、D.W.检验相关结果

4.5. 异方差检验

对于上述模型，如果随机干扰项的方差不再是常数而各不相同，则认为出现了异方差性，而异方差性可能会造成模型的预测失效。因此，本文运用Eviews对模型进行了怀特检验以验证模型是否存在异方差性。先对模型作OLS回归，并得到模型残差项的平方 $e_i^2$，然后做如下辅助回归：

$e_i^2=m_0+m_1\ln x_1+m_2\ln x_2+m_3\ln x_3+m_4\ln x_4+m_5\ln x_1^2+m_6\ln x_2^2+m_7\ln x_3^2+m_8\ln x_4^2+{\epsilon }_t$

要检验的同方差性假设为：

$H_0:m_1=m_2=\cdots =m_6=m_7=m_8=0$

检验后我们得到的p值为0.0000 < 0.05，因此我们拒绝原假设，认为模型存在异方差。

下面进行加权最小二乘法异方差修正。我们选取残差绝对值的倒数作为权重，再次进行怀特检验，发现此时的p值为0.9718，因此我们接受原假设，模型不存在异方差。此时的模型如下：

$\ln y=2.411830-0.043670\ln x_1-0.012085\ln x_2-0.646838\ln x_3-0.110651\ln x_4$

4.6. 模型修正后检验

进行VIF方差膨胀因子检验及相关系数矩阵检验：

综上，如表4，模型设计通过共线性检验，解释变量间基本不存在多重共线性；样本数据通过残差检验，残差项基本不存在序列相关性，服从正态分布，符合OLS的基本假设。所以，我们可以认为上述模型在经过多次修正后已经符合要求，其结果具有可信度，可以用于后面的分析。

Table 4. VIF variance inflation factor test and correlation coefficient matrix

表4. VIF方差膨胀因子检验与相关系数矩阵

4.7. 模型结果分析

如表5，通过上述的参数估计值，我们得到如下模型：

$\ln y=2.411830-0.043670\ln x_1-0.012085\ln x_2-0.646838\ln x_3-0.110651\ln x_4$

Table 5. Model fitting results

表5. 模型拟合结果

4.8. 重建模型检验

4.8.1. 经济意义检验

债券规模的回归系数约为−0.004，P = 0.000 < 0.01，在1%的水平下显著，说明绿色债券发行规模越大，绿色债券发行利率越低。原因可能是绿色债券发行规模与发行期限等其他因素不稳定，或债券规模单位选择不合适。

债券期限的回归系数约为−0.001，P = 0.000 < 0.01，在1%的水平下显著，说明绿色债券发行期限越长，绿色债券发行利率越低。可能是由于绿色债券市场发展时间较短，发行期限波动较大。

债券评级的回归系数为−0.64，P = 0.000 < 0.01，在1%的水平下显著，说明绿色债券评级越高，绿色债券发行利率越低，说明绿色债券评级可以反映绿色债券的风险状况，从而影响发行利率。

专项指引政策的回归系数为−0.11，P = 0.000 < 0.01，在1%的水平下显著，说明专项指引政策的数量会影响绿色债券的发行利率，专项指引政策的数量越多绿色债券发行利率越低，较好地检验了绿色债券的政策性。

4.8.2. 统计检验

拟合优度检验

由结果可知，模型的可决系数为0.900371和修正的可决系数为0.905842都较为接近1，这说明模型对样本的拟合效果较好。

t检验

分别针对 $H_0:a_i=0\left(i=1,2,3,4\right)$，给定显著性水平 $\alpha =0.10$，在t分布表中查出临界值为1.28。由结果可得，a对应的统计量的值分别为：560.2349、−93.71747、−23.15088、−339.7860，绝对值均大于1.28。这说明在给定的显著性水平 $\alpha =0.10$ 下，应分别拒绝原假设H₀，即保证其他变量不变的情况下，解释变量债券规模，债券期限，债券评级以及专项指引政策分别对被解释变量绿色债券票面利率影响显著。

F检验

针对 $H_0:a_1=a_2=a_3=a_4=0$，即所有解释变量联合起来对被解释变量的影响不显著。给定显著性水平 $\alpha =0.10$，在F分布表中查出对应的临界值约为3.3，而模型检验结果得到F = 78.46 > 3.3，应拒绝原假设H₀，说明回归方程显著，即债券规模，债券期限，债券评级以及专项指引政策等变量联合起来，确实对绿色债券票面利率有显著影响。

4.9. 结论及建议

本文经过实证分析，得出以下结论：专项指引政策、债券评级等越高或越好，绿色债券发行利率越低。从政府的角度，如果想降低整体绿色债券发行利率则要出台更多的相关绿色债券支持政策，对于绿色债券的整体发行过程要有更好的指引效果。

5. 全国绿色金融影响时间序列分析

5.1. 样本选择说明

从全国经济与环境发展现状可以知道，由于部分地区绿色金融产品和服务尚待完善、绿色金融发展缺乏良好的市场环境和绿色金融发展政策配套措施欠缺等问题存在，政府和金融机构无法提供直接的绿色金融发展和环境水平相关性的数据作为分析。因此，本文选取全国每万元GDP的综合能耗作为环境治理水平的指标，即可以反映绿色金融对环境治理的影响。

万元GDP能耗是指一个地区在报告内(如一个季度、一年等)创造每一万元所耗费的综合能源消费量，公式：万元GDP能耗 = 综合能源消费量(吨标准煤)/GDP(万元)，单位为吨标准煤/万元；综合能源消费量为一个地区一定时期的居民生活所耗费的电力、油品、煤品等能源品种折算成标准煤的合计数，GDP按不变价计算。因此本文认为使用万元GDP综合能耗作为环境治理水平的指标，反映绿色金融对环境治理的影响是合理的 [10]。

5.2. 平稳性检验

这里初步选择1978~2021年全国每万元GDP的综合能耗的时间序列数据建立模型，选择ACF自相关系数、PACF偏自相关系数检验以及单位根检验对时间序列的平稳性进行检验，利用Eviews作为工具，使用代码实现上述功能，对数据进行初步分析。

5.2.1. 数据分析

如图4为全国每万元GDP的综合能耗随时间变化的图像，我们可以初步观察到数据一直是下降的。而根据平稳时间序列均值、方差为常数的性质，平稳序列的时序图应该显示出该序列始终在一个常数值附近随机波动，而且波动范围有界的特点。因此我们得出，该时间序列不平稳。再通过自相关系数及偏自相关系数检验分析后，应当对时间序列进行平稳性处理 [11]。

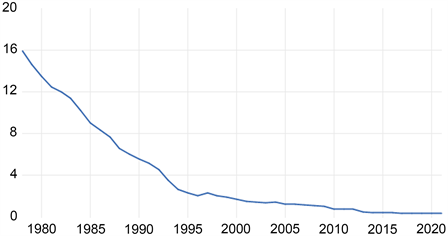
Figure 4. Time series changes of raw data of comprehensive energy consumption per 10,000 Yuan of GDP in China

图4. 全国每万元GDP的综合能耗原始数据时间序列变化

从图5我们可以发现，序列的自相关系数递减到零的速度相当缓慢，在很长的延迟时期里，自相关系数一直为正。而偏自相关系数的波动性较小，不存在明显的变化趋势，并且出现拖尾现象。

5.2.2. 平稳化处理

如果观察序列的时序图，显示出该序列有明显的趋势性或周期性，那他通常不是平稳序列。

图6是非平稳的，图7是平稳的。二阶差分后全国每万元GDP的综合能耗数据随时间变化有一定趋势及规律，保留了原始数据特性。

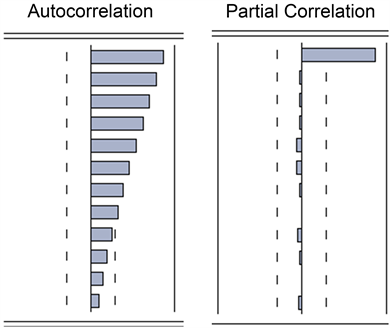
Figure 5. ACF and PACF graph of the original data of comprehensive energy consumption per 10,000 Yuan of GDP in China

图5. 全国每万元GDP的综合能耗原始数据ACF、PACF图

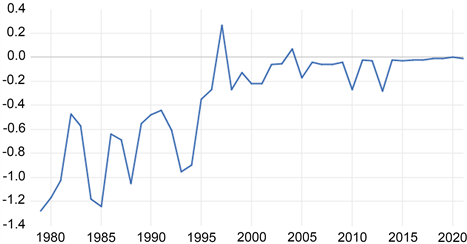
Figure 6. First-order difference data time series changes

图6. 一阶差分数据时间序列变化

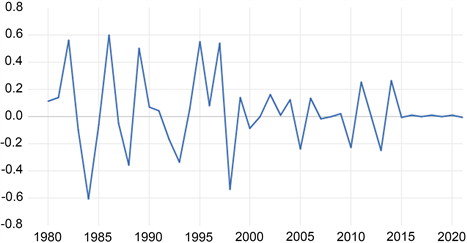
Figure 7. Second-order difference data time series changes

图7. 二阶差分数据时间序列变化

如图8所示，经过二阶差分后，全国每万元GDP的综合能耗的ACF图以及PACF图的波动较小，不存在明显的变化趋势，出现一定的截尾与拖尾现象，可以认为时间序列稳定，通过ACF、PACF检验。

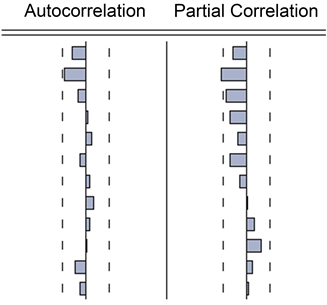
Figure 8. ACF and PACF map of the second-order difference of comprehensive energy consumption per 10,000 Yuan of GDP in the country

图8. 全国每万元GDP的综合能耗二阶差分后ACF、PACF图

5.2.3. 单位根检验

对上述二阶差分后的时间序列数据进行单位根检验，计算得到二阶差分时间序列数据如表6所示。

Table 6. Unit root test results of second-order difference time series data

表6. 二阶差分时间序列数据单位根检验结果

由表可以看到，计算出来的统计量的值显著小于0.05，所以我们认为此时的序列平稳，确定ARIMA(p,d,q)模型的最终合适阶数d等于2。并且可以进行下一步分析。

5.3. 白噪声检验

如表7所示，对二阶差分过后的全国每万元GDP的综合能耗运用Ljung-Box方法进行白噪声检验。可以发现12阶滞后项的LB检验p值均小于0.05，拒绝原假设，即认为所检验时间序列不是白噪声序列，通过白噪声检验，具有研究价值，可以进行进一步分析。

Table 7. LB test results for second-order difference time series data

表7. 二阶差分时间序列数据LB检验结果

5.4. 模型识别

我们研究的序列是单变量时间序列。建模的目的是通过使用变量的历史值和当前值的随机误差项来预测变量的变化前景。假定随机误差项在统计上是独立的，并且在不同时间与正态分布一致。对于时间序列预测，首先找到最佳预测模型，所以预测的关键是顺序的确定和参数的估计。

计算出样本自相关系数和偏自相关系数的值之后，就要根据它们表现出来的性质，选择适当的ARMA模型拟合观察值序列。这个过程实际上就是要根据样本自相关系数和偏自相关系数的性质估计自相关阶数和移动平均阶数，因此，模型识别过程也称为模型定阶过程。如图，从二阶差分后的自相关图和偏自相关图可以看出，全国每万元GDP的综合能耗时间序列数据呈现出ACF值迅速跌入置信区间，没有收敛趋势，显示出拖尾性；PACF值迅速跌入置信区间，没有收敛趋势，显示出拖尾性。所以考虑选用ARMA模型拟合时间序列，又考虑到是二阶差分后的时间序列，因此对原始序列使用ARIMA模型。

5.5. 参数选择

通过观察图，二阶差分后时间序列数据ACF在2阶后衰减趋于零，PACF在4阶后衰减，差分阶数为2，因此q = 4，p = 2，n = 2，故建立ARIMA(2,2,4)模型，最终建立时间序列数据的ARIMA模型。

5.6. 模型检验

主要针对模型进行变量显著性及残差检验，计算相关检验值，通过绘制残差正态QQ图验证残差是否符合正态分布以及使用BP检验残差序列是否为白噪声序列、Ljung-Box方法检验残差的自相关系数是否都为零，并通过对变量进行t检验计算p值判断显著性。

5.6.1. 检验数据

全国每万元GDP的综合能耗原始时间序列数据的ARIMA模型的一些检验值，各误差在可接受的范围内，模型拟合性能良好。

5.6.2. 残差检验

首先绘制残差正态QQ图，如图9所示，样本残差基本服从正态分布，符合模型对残差服从均值为零的正态分布的基本要求。

Figure 9. Residual QQ plot

图9. 残差QQ图

使用Ljung-Box方法检验残差的自相关系数是否为零，根据原始时间序列结果的p值为0.6951，说明模型的残差没有通过LB检验，即可以认为残差的自相关系数为零，ARIMA模型能较好地拟合本数据。但模型拟合度有待提高，因而尝试对增值税减税的时间序列数据建立GARCH模型，进行辅助分析。

5.6.3. 变量显著性检验

如表8所示，全国每万元GDP的综合能耗时间序列建立的ARIMA模型拟合结果的各变量t检验p值均大于0.05，通过t检验，认为各变量在模型中均显著，可以很好地解释模型，模型拟合效果良好。

5.6.4. 模型优化

尝试对全国每万元GDP的综合能耗原始时间序列数据建立GARCH模型，使用Ljung-Box方法检验残差的自相关系数，p值为0.54，说明模型的残差没有通过显著性检验，即可以认为残差的自相关系数为零，GARCH模型能较好地拟合本数据。详细结果将在后文给出。

Table 8. Income tax deduction ARIMA model variable t-test results

表8. 所得税减税ARIMA模型变量t检验结果

5.7. 模型结果分析

5.7.1. 全国每万元GDP的综合能耗时间序列建立ARIMA模型

ARIMA模型的原始模型为：

$\{\begin{array}{l}\Phi \left(B\right){\nabla }^d{x}_t=\Theta \left(B\right){\epsilon }_t\\ E\left({\epsilon }_t\right)=0,Var\left({\epsilon }_t\right)={\sigma }_{\epsilon }^2,E\left({\epsilon }_t{\epsilon }_s\right)=0,s\ne t\\ E{x}_s{\epsilon }_t=0,\forall s<t\end{array}$

通过上述分析，全国每万元GDP的综合能耗原始时间序列数据建立ARIMA模型通过各项检验，能较好地拟合数据，模型如下：

$\begin{array}{c}{\nabla }^2{Y}_t=1.003631{\nabla }^2{Y}_{t-1}-0.664803{\nabla }^2{Y}_{t-2}+0.050354{\nabla }^2{Y}_{t-3}-0.137936{\nabla }^2{Y}_{t-4}\\ +{\epsilon }_t-1.560858{\epsilon }_{t-1}+0.849602{\epsilon }_{t-2}\end{array}$

如表9，上述模型各估计值标准差较小，具有良好的拟合程度，再次证明模型建立的正确性。具体观察结果，通过数理分析并结合相关理论可以知道全国每万元GDP的综合能耗确实具有时间相关性，过去的数据会影响当期数据，同时往往上上期的数据影响程度大于上期数据的影响程度大于再过往的数据，这说明绿色金融政策真正产生效果具有一定的时间滞后性。

Table 9. ARIMA model results

表9. ARIMA模型结果

5.7.2. 模型预测

我们运用ARIMA(2,2,4)模型，利用1978~2019年的数据，对我国2020年和2021年的全国每万元GDP的综合能耗2阶差分值进行预测。

如表10，通过验证2020~2021的数据，预测结果相对误差均小于3%，这表明预测效果良好。所以，我们选择ARIMA(2,2,4)模型对我国未来3年的每万元GDP的综合能耗进行预测，结果如下表11：

Table 10. ARIMA model fit

表10. ARIMA模型拟合

Table 11. ARIMA model predictions

表11. ARIMA模型预测

由此可以看出，我国未来3年的每万元GDP的综合能耗继续保持缓慢下降的趋势。

5.7.3. 模型改进

GARCH模型的原始模型为：

$\{\begin{array}{l}{x}_t=f\left(t,x_{t-1},x_{t-2},\cdots \right)+{\epsilon }_t\\ {\epsilon }_t=\sqrt{h_t}{e}_t\\ h_t=\omega +{\displaystyle \underset{i=1}{\overset{p}{\sum }}{\eta }_i{h}_{t-i}}+{\displaystyle \underset{j=1}{\overset{q}{\sum }}{\lambda }_j{\epsilon }_{t-j}^2}\end{array}$

通过上述分析，全国每万元GDP的综合能耗原始时间序列数据建立GARCH模型通过各项检验，能较好地拟合数据，根据拟合结果建立如下模型：

${\sigma }_t^2=-3.11\times {10}^{-6}+0.110034{\epsilon }_{t-1}^2+1.120165{\sigma }_{t-1}^2$

如表12，上述模型再次印证全国每万元GDP的综合能耗确实具有时间相关性，过去的数据会影响当期数据，它们之间的波动性也具有相关性，全国每万元GDP的综合能耗会影响当期全国每万元GDP的综合能耗的效果，从而影响绿色金融的实施效果。

Table 12. GARCH model

表12. GARCH模型

5.8. 结论及建议

5.8.1. 结论

全国每万元GDP的综合能耗具有时间相关性，过去数据会影响当期数据。同时绿色金融政策的实施具有一定时间滞后性，往往上上期的数据影响程度大于上期数据的影响程度大于再过往的数据。此外，往期的数据对当期数据产生正向影响，使得综合能耗的下降越来越快。在未来，全国每万元GDP的综合能耗将进一步降低，说明我们绿色金融的影响效果进一步提升，一直向好发展。

5.8.2. 建议

1) 以政策性措施为导向，促进绿色金融的发展

由上述分析结果我们可以得知，绿色金融政策虽有一定的时间滞后性，但是政策性措施对产业发展过程中起导向作用。首先，根据国际发展经验，效仿发达国家成熟的做法，成立政策性的生态银行，对环保、清洁能源、风能及太阳能等新能源生产和消费者给予一定额度的补贴，对这些节能环保和新能源企业进行“输血”支持，促使其完善绿色生产技术，注重绿色研发，引导企业运营规范化，提升绿色企业文化，促使其不断提升绿色发展质量，从而带动绿色金融的发展。

2) 不断增强资本市场“造血”功能，扩大绿色金融的融资规模

发展多层次资本市场体系，对绿色金融也能起到良好的催化作用。强化资本市场对绿色产业发展的“造血”功能，已成为当前资本市场发展的重要方向。所以，资本市场应当进行结构性调整，对具有核心技术优势及竞争力的企业降低进入门槛，为绿色金融提供更多的发展契机。

3) 加大环境保护投资力度

虽然有一定时间滞后性，但是加大环境保护投资力度的确可以促进绿色金融的发展。加大环境保护投资有利于环保方面资金的流动，从而促进绿色金融发展的灵活性与可持续发展性，进而推动绿色金融发展，同时环境质量的不断改善也会为绿色金融的发展提供外在动力，刺激对绿色金融需求 [12]。

参考文献