1. 引言
水声信道是目前难度最大的无线通信信道之一 [1],水下声波较低的传播速度以及水下复杂多变的环境都会对水声信号造成干扰。而浅海信道中强烈的多径效应更是给水声通信的工程实践带来了巨大挑战,为了对抗多径效应的干扰,通常需要对信道进行自适应均衡。信道均衡的目的是对接收信号进行补偿,抑制多径传输带来的码间干扰,从而尽可能地恢复发送信号。均衡器的抽头系数通常采用LMS或RLS算法进行调节,其中RLS算法性能优于前者,但与之对应的是巨大的计算量,而LMS算法性能虽比不上RLS算法,但其计算量小,且易于工程实现,因此需根据实际情况进行选择。
本文将在FPGA上搭建基于LMS算法的自适应滤波器,并利用BELLHOP模型对水声信道进行建模,模拟真实海况对水声信号的影响。最后将经过水声信道模型的信号作为均衡器的输入,分析LMS自适应滤波器在水声信道均衡中的性能。
2. 水声信道建模
通常可将水声信道看作一个线性、随机时变的滤波器,该滤波器的冲击响应为h(p, t, f),其中p为位置参数,t为时间,f为频率。因此,接收信号可表示为发送信号与信道响应的卷积 [2],即:
(1)
要获取水声信道的具体参数,需要从声场模型来分析,一般常用的声场模型有射线理论模型、简正波模型、多途扩展模型、快速场模型、抛物线方程模型等五种 [3]。目前水声领域应用最广泛的声学模型有简正波模型和射线理论模型,其中简正波模型更为精确,但由于其理论与计算过于繁琐,相比之下射线理论模型物理意义直观且易于计算,故在工程应用中多用射线理论模型。
在高频情况下,可将声波的传输过程看作一束拥有N条与等相位面垂直的射线形成的传播,高频条件指的是 [2]
(2)
其中f为声波频率,c为水下声速,z为声源深度。本文在仿真过程中选取的声源深度为50 m,在此深度下,声速约为1500 m/s,由此可计算出下限频率约为300 Hz,而选用的载波频率为35 kHz和30 kHz,满足该高频条件,故可基于射线理论模型对水声信道进行建模。
2.1. 射线声学理论
在理想均匀介质中,声波的波动方程为 [4]:
(3)
其中
为拉普拉斯算子,p为势函数,c为声速。在稳态声场中,波动方程可简化为与时间无关的形式:
(4)
式(4)即为亥姆霍兹(Helmholtz)方程,其中
是波数,
为波长,
为声源角频率,射线声学理论是一定条件下对此方程的近似求解。
射线模型通过两个方程来确定声场的路径和强度,对于简谐过程的波动方程:
(5)
其中
为参考点波数,n为与环境有关的折射率。假设其解得形式为:
(6)
其中A为声压幅度函数,S为相位函数。将式(6)代入式(5)可得
(7)
(8)
当满足
,即在一个波长内声速变化不大的条件时,式(7)中第二项可以省略,如此便得到:
(9)
式(9)称为程函方程,确定了声线的方向,声线方向定义为等相面
的法线方向。
对于式(8),由于
(10)
故
(11)
式(11)称为强度方程,由程函方程和强度方程即可求解出波动方程的近似解,如此便可近似求解出水下声场的各项参数。
2.2. 基于BELLHOP的水声信道建模方法
由上文可知程函方程仅在
时成立,即在一个波长内声速变化不大。显然声波频率越高越容易满足这一条件,但为了使所得的水声信道模型同样适用低频情况,则需采用新的建模方法。
BELLHOP是利用射线和高斯波束跟踪预测海洋环境中声压场的模型,它通过高斯波束追踪法,求解出水平非均匀的水声环境中的声场。高斯波束射线追踪方法的核心思想是将水下声场中的每一条声线和高斯强度的分布进行联系起来,这些声线是高斯声束的中心线,这些声线不仅能平缓地过度到水下声影区,也能平滑地穿过水下声场的焦散线,如此得到的水声信道模型更准确,更符合实际情况 [5]。BELLHOP整体结构如图1所示:

Figure 1. Overall structure of BELLHOP
图1. BELLHOP整体结构图
BELLHOP [6] 模型的输入文件需要能够描述发送端和接收端的环境和几何特性,其输入文件包括环境文件(文件后缀为.env)、水深文件(文件后缀为.bty)、声速分布剖面分布文件(文件后缀为.ssp)以及海洋底部反射系数文件(文件后缀为.brc)。通常情况下只需输入一个环境文件,该文件包含了声速剖面以及相关的海底信息,同时也可添加水深文件来确定不同位置的水深。当海洋中的声速处在一个变化的范围中时,可通过添加一个声音速度剖面分布文件将声速列成规范性的列表。如果需要指定一个通过任意底部反射系数来表征的底部,那么必须提供一个海洋底部反射系数文件。
BELLHOP模型的输出文件包括用于描述声线和本征声线的声线文件(文件后缀为.ray,通常用来获得信号在信道中传播过程中的能量感应)、用于描述声线传播损失的传播损失文件(文件后缀为.shd)以及用于描述声线到达的时间–幅度序列参数的到达文件(文件后缀为.arr)。该文件中的信息可用于描述信道的冲击响应,将其与发送端信号的时间序列进行卷积,即可得到接收端信号的时间序列。

Figure 3. Time series of sender and receiver
图3. 发送端与接收端时间序列
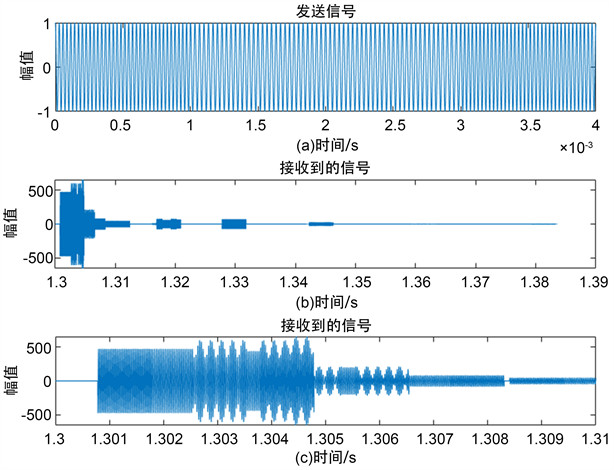
Figure 4. Diagram of inter symbol interference
图4. 码间串扰示意图
本文以Matlab作为BELLHOP的运行平台,BELLHOP模型以环境文件作为唯一输入文件。仿真的通信环境为:水深100 m,发送机与接收机的深度均为50 m,二者直线距离2 km,发送信号频率为35 kHz。图2为上述模拟条件下通过BELLHOP模型计算出的多径信道响应,图3为发送端与接收端信号的时间序列。
图2中横坐标最小值为1.3,是因为发送机与接收机之间距离为2000 m,水下声速约为1500 m/s,故接收端在经过1.33 s时延之后才能接收到信号。图3(a)为发送的原始信号,图3(b)、图3(c)均为接收到的信号,其中图3(c)为图3(b)放大所得。从图3(b)、图3(c)可看出,发送的信号经过不同路径传播,在接收端可接收到若干个不同时延的信号,此为多径效应。若连续发送多个码元,多径效应会造成码间串扰,如图4所示。
图4(a)为发送的原始信号,图4(b)、图4(c)均为接收到的信号,从图4(c)可看出码间串扰使信号发生了畸变。采用自适应滤波器对信道进行均衡可有效解决这一问题。LMS算法作为主流的均衡算法,具有结构简单、算法复杂度低、便于硬件实现等优点,故本文采用LMS算法对信道进行均衡。
3. LMS自适应滤波器的FPGA实现
LMS自适应滤波器由FIR滤波器和LMS自适应算法两部分组成,且FIR滤波器的各抽头系数由LMS算法实时调整,最终使FIR滤波器的输出信号收敛。LMS自适应滤波器结构如图5所示。
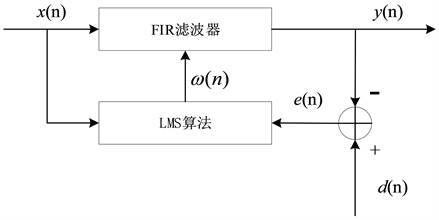
Figure 5. LMS adaptive filter structure diagram
图5. LMS自适应滤波器结构图
图中
为待处理信号序列,
为输出信号,
为期望信号,
为滤波器系数,下同。
FIR滤波器的本质就是一个标准的乘加运算集,因此分布式算法[]很适合用于FIR滤波器的设计。分布式算法的限制条件之一是每个乘法运算中必须有一个乘数为常数,一个乘数为常数的乘法可采用查找表来实现,而FPGA正是基于查找表构建的,因此很适合在FPGA上用分布式算法实现FIR滤波器,如此既可节省硬件资源,又能提高运算速度。
LMS算法基于最小均方误差准则,在梯度法的基础上,通过改进均方误差梯度的估计值计算方法,取单个误差样本平方的梯度作为均方误差的估计值 [7]。并将维纳–霍夫方程转换为一组递推公式,即
(12)
其中
为误差信号,
为加权向量更新时的步长因子。该递推公式仅包含加减法和乘法运算,巧妙地避开了原来的矩阵运算,从而更有利于在FPGA上实现。LMS自适应滤波器的一般实现结构如图6所示 [7],图中虚线框内为FIR滤波器模块,其余部分为LMS权值更新模块。
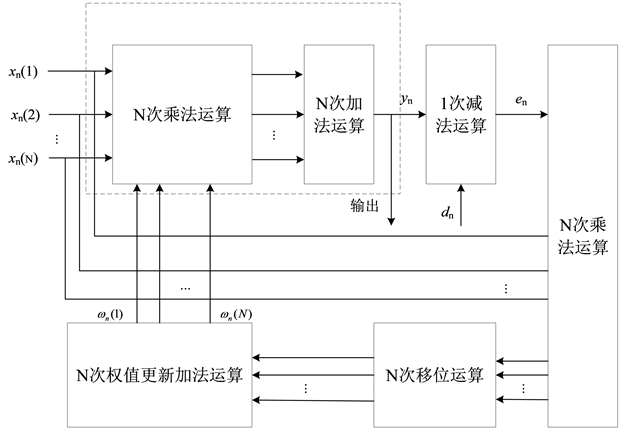
Figure 6. Implementation structure of LMS adaptive filter
图6. LMS自适应滤波器的实现结构
从图6可看出,若所有计算均以串行方式进行,需要进行2N次乘法运算、2N + 1次加减法运算、以及N次移位计算,这样只需调用2个乘法器、3个加减法器和1个寄存器,能有效地节省硬件资源。但LMS算法的所有运算需要在一个数据周期内完成,当采样输入数据速率较高或权向量位数较多时,会因为权值更新过慢而影响滤波性能。同样,也可采用并行运算的方式实现图6所示结构,在这种情况下,完成一次权值更新只需进行2次乘法、3次加减法和1次移位运算,相比串行结构大大降低了一次权值更新所需的顺序计算量,但需要的硬件资源变成了2N个乘法器、2N + 1个加减法器和N个寄存器。
LMS算法虽然只包括加减法以及乘法运算,但乘法器资源在FPGA中数量有限,且乘法运算速度受限,因此提出了针对硬件实现的简化算法,其中包括符号LMS算法和符号化回归LMS算法 [8]。符号LMS算法将式(12)中的
用其符号代替,得到的递推关系为:
(13)
符号化回归LMS算法将式(12)中的
用其符号代替,得到的递推关系为:
(14)
同时,将步长因子
取值为2的负整数次幂,这样在更新滤波器系数的计算过程中不再需要乘法运算,能够减少N次乘法运算,提高LMS算法的运算速度。但是以上两种算法性能随机性较大,在工程实践中需要先对其进行仿真,经过比较之后选取性能较好的一个。
对两种简化算法进行Matlab仿真之后,选用的简化算法为符号化回归LMS算法,步长因子
取1/128,输入与输出数据长度均为16比特,滤波器抽头数为8。结合上文的分析可知,FPGA以串行方式实现LMS算法需要进行的运算步骤为:
步骤一:计算y(n),需进行一次16比特*16比特的乘法运算和8个32比特数据的加法运算;
步骤二:计算e(n),需进行一次减法运算;
步骤三:计算权值更新(dw),需进行一次判断与取反操作;
步骤四:更新滤波器抽头系数,需进行一次加法运算。
在分配各运算步骤所需时钟周期时,基本原则是使各步骤的运算尽可能相近,因此本文各时钟周期的运算量分配方案为:步骤一中乘法运算使用乘法器IP核实现,流水线设置为2级,占用两个时钟周期,8个32 bit的加法运算分为2次4个32 bit并行加法及1个32 bit加法运算,其中4个32 bit加法运算占用一个时钟周期,1个32 bit加法运算与步骤二在同一时钟周期内完成,占用1个时钟周期,步骤三和步骤四各占用一个时钟周期。综上,完成LMS算法的一次迭代需占用6个时钟周期,因此,FPGA系统时钟频率应为数据抽样频率的6倍。最终在FPGA上实现的LMS自适应滤波器原理图如图7所示,表1展示了该滤波器消耗的硬件资源。

Figure 7. RTL schematic diagram of LMS adaptive filter
图7. LMS自适应滤波器RTL原理图

Table 1. Hardware resources consumed by LMS adaptive filter based on FPGA
表1. FPGA实现 LMS自适应滤波器消耗的硬件资源
4. LMS自适应滤波器性能分析
本文仿真所采用的水声通信系统模型为:对信号进行FSK调制,调制信号经过BELLHOP水声信道模型之后得到受干扰的接收端信号,再利用Modelsim对LMS均衡器模块进行功能仿真,得到滤波之后的信号。
图8为信号比对示意图,a为发送的调制信号,b为经过水声信道后接收端信号,c为经过均衡之后的信号,由于系统采用FSK调制方式,信号的幅值对系统的影响很小,故图a,b,c中的信号为归一化处理后的信号波形,不代表真实幅值。图9为未经均衡信号的幅频特性曲线,图10为均衡后信号幅频特性曲线。同样,图9和图10中的幅频特性曲线主要展示不同频率分量信号幅值的相对关系。可看出本文设计的LMS自适应滤波器能够较好地消除水声信号中的噪声并恢复出原始信号。

Figure 9. Amplitude-frequency characteristic curve of received signal
图9. 接收信号幅频特性曲线

Figure 10. Signal amplitude-frequency characteristic curve after filtering
图10. 滤波后信号幅频特性曲线
5. 总结
本文从理论层面对水声信道进行分析,在Matlab平台利用BELLHOP模型对水声信道进行建模仿真,并在FPGA平台上实现了LMS自适应滤波器。将BELLHOP模型的输出信号作为滤波器的输入在Modelsim中进行仿真,对比滤波前后信号的频谱图可得,本文设计的自适应滤波器器能够较好地消除噪声信号与多径效应对信号造成的干扰,对水声信道能够起到较好的均衡作用。
NOTES
*通讯作者。