1. 引言
一般来说,一些量子引力建议 [1] [2] 在实践中极难测试,因为量子引力效应仅在普朗克尺度下才可感知 [3]。但极值加速度给出了另一种增强量子引力效应的方案。与极值速度c类似,假设存在极值加速度β,任何物体的加速度都不能超过这个极限β。太阳系中的极值加速度β = 2.961520e+10 (m/s/s)。因为这个极值加速度是一个大数字,任何与β相关的效应都很容易测试,包括量子引力测试。在相对论范畴内研究极值加速度需要结合相对论物质波概念 [4] [5] [6],主要涉及大尺度的空间和时间 [7] [8] [9],主要观察对象是地球和太阳等 [10] - [15],涉及空间碎片 [16] - [25] 和大气运动以及全球气候变化 [26] [27]。在地球研究方面,可以从南极冰层样本中对过去80万年的温度和二氧化碳水平进行详细的气候变化计算。在这个时间范围内,地球温度随着冰川作用和二氧化碳水平的变化而升高或降低 [27]。尽管与Milankovitch假说大致一致,但该假说并未解释许多具体观察结果。
本文提出了一种将极值加速度与量子理论联系起来的方法,提出了一种行星尺度的相对论物质波模型。该相对论物质波模型用于计算太阳黑子周期;拟合计算全球气候变化的大尺度周期;估算过去一个世纪全球气温上升值。
2. 如何把极值加速度与相对论物质波联系起来
在相对论中,光速c是极值速度,任何物体的速度都不能超过这个极限c。一个粒子的四维速度u满足
(1)
无论哪一种粒子(电子,分子,中子,或夸克),它们的四维速度u都具有相同的数量大小,即|u| = ic。在相对论时空(x1, x2, x3, x4 = ict)中,四维速度u具有平等性:对所有的粒子,四维速度u具有相同的数量大小,这叫做“速度平等性原理” [28] [29]。
粒子的加速度a为
(2)
假如存在粒子的极值加速度β,没有任何粒子的加速度能超过这个最大极值加速度β。上式两边同时减去β2,我们有
(3)
它可以写成
(4)
现在,上式左边包含五项,粒子的相对论加速度可以看成五维加速度,定义为
(5)
这里a5是新定义的第五维加速度,其五维相对论空间是(x1, x2, x3, x4 = ict, x5),这样我们有
(6)
它意味着任何粒子的相对论加速度α的数量大小都取相同的值:|α| = iβ (常虚数)。
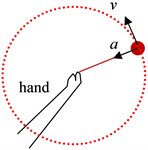
每一个粒子的相对论加速度α的数量大小都取固定值:|α| = iβ,每一个粒子的相对论速度u的数量大小也取固定值:|u| = ic,这是一种怎样的运动图像?在现实世界中,当一个小球做匀速圆周运动的时候,它具有常切向速度v和常向心加速度a,如图1(a)所示。
 (a)
(a) 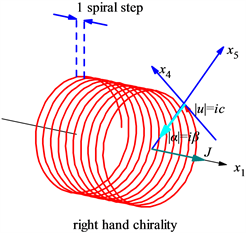 (b)
(b)
Figure 1. (a) A hand rotates a ball moving around a circular path at constant speed v with constant centripetal acceleration a. (b) The particle moves along the x1 axis with the constant speed |u| = ic in the u direction and constant centripetal force in the x5 axis at the radius iR (imaginary number), the coordinate system (x1, x4 = ict, x5 = iR) establishes a cylinder coordinate system
图1. (a) 手转动小球使其做匀速圆周运动的时候,小球具有常切向速度v和常向心加速度a。(b) 一个沿着x1轴以速度v做匀速运动的粒子,它在图中沿着u方向以常速度|u| = ic运动,在x5轴方向以常加速度|α| = iβ做半径iR (虚数)的圆周运动,它的坐标系(x1, x4 = ict, x5 = iR)构成一个柱坐标系
类似于匀速圆周运动的小球,如图1(b)所示,考虑一个沿着x1轴以速度v做匀速运动的粒子,它在图中沿着u方向以常速度|u| = ic运动,在x5轴方向以常加速度|α| = iβ做半径iR (虚数)的圆周运动,它的坐标系(x1, x4 = ict, x5 = iR)构成一个柱坐标系,在其中,粒子沿着x1轴以速度v做螺旋运动。根据我们熟知的向心加速度公式a = v2/r,在x4~x5平面的向心加速度是
(7)
所以,在这个(x1, x4 = ict, x5 = iR)柱坐标系中粒子的轨迹形成一个螺旋图形,称为加速度卷,粒子运动速度v越快,螺旋步距越长。
定理:可视化的加速度卷承载相对论物质波。
证明:图1(b)中的加速度卷就像一个钢丝弹簧,可以用一个波函数来描述其弹性波;粒子向前运动1个螺旋步距(spiral step),对应波函数的相位增加2π,一个螺旋步距对应一个螺旋周长是2π (iR)。既然粒子在螺旋线上的每个微小位移是|u|dτ= icdτ (在四维速度u的方向上),波函数相位增加量的计算公式为
(8)
代入半径R,波函数ψ表示为
(9)
在相对论理论中,我们知道沿着dτ的积分需要换算成现实世界的线积分,也就是
(10)
所以波函数ψ表达式为
(11)
对应不同种类的粒子,这个波函数有不同的解释。对于电子,最大极值加速度β用普朗克常数(Planck constant)来替换,那么波函数ψ表示为
(12)
注意到mu4dx4 = −Edt,上面这个方程强烈建议上述波函数ψ就是现实世界的德布罗意物质波(de Broglie matter wave)。在图1(b)中,电子的加速度卷有2种:顺时针加速度卷和逆时针加速度卷,即相对论的德布罗意物质波具有手征性:左螺旋手征性和右螺旋手征性。角动量J的方向会与电子前进的x1方向稍微不同,因为角动量J在绕着x1方向做进动。[证毕]
利用极值加速度概念,德布罗意物质波可以推广到行星轨道量子化,行星尺度的引力的相对论物质波表示为
(13)
极值加速度β将由实验观察来确定。本文将尝试用这种波函数来替代太阳系和地球大气中的行星尺度波,这种波函数被称为“加速度卷波”。
3. 如何确定极值加速度
在行星或卫星的玻尔轨道模型中,如图2所示,根据行星尺度的引力中的相对论物质波,给出了圆轨道的量化条件:
(14)

Figure 2. A planet 2D orbit around the sun, an acceleration-roll winding around the planet
图2. 一颗行星绕太阳运行,一个绕着行星旋转的加速卷
用玻尔轨道模型研究了太阳系、木星卫星、土星卫星、天王星卫星和海王星卫星这五个不同的多体系统。在拟合图3所示的观测数据后,获得了它们的最终的极值加速度,写在表1中。图3(a)、图3(b)、图3(c)、图3(d)和图3(e)中预测的量化蓝线与靠近中央的行星或卫星的实验观测结果非常一致。

Table 1. Planck-constant-like constant h, N is constituent particle number with smaller orbital inclination.
表1. 类普朗克常数的常数h,N是轨道倾角较小的组成粒子数
除此之外,我们的兴趣转移到表1中的常数h,其定义为
(15)
在总质量为M的多体系统中,某个行星的质量为m,并以v的速度移动,很容易发现,对于这个行星(或卫星),德布罗意物质波的波长应修改为
(16)
其中h是类普朗克常数的常数。通常,总质量M近似等于中心恒星的质量。我们发现,在图3中,这种推广的相对论物质波可以正确地给出量子化的轨道。关键是,不同系统具有几乎相同的类普朗克常数的常数h,如表1中所示,平均值为3.51e−16 m2∙s−1∙kg−1,至少具有相同的大小!加速度卷波是行星尺度的广义的相对论物质波。
在图3(a)中,蓝色直线表示太阳、水星、金星、地球和火星之间的线性回归关系,其量化参数为hM = 9.098031e+14 (m2/s)。极值加速度拟合为β = 2.961520e+10 (m/s2)。其中,n = 3, 4, 5, ∙∙∙被分配给太阳系行星,太阳被分配了量子数n = 0,因为太阳处于中心态。
4. 太阳的中心态的光学模型
我们为每颗行星分配了一个量子数,太阳也被分配了一个量子数n = 0,将太阳视为太阳系中的第0颗行星——并处于中心态。
作为行星尺度的相对论物质波,它的加速度卷波为
(17)
在中心态n = 0时,如果加速度卷波的相干长度足够长,则当粒子在时空中的闭合轨道上运动时,其头部可能与其尾部重叠,如图4(a)所示,在重叠区,其头部和尾部之间的加速度卷波将发生相互干涉。由于加速度卷波围绕着时间轴旋转并与自身重叠,重叠的波动由下式计算
(18)
式中N是重叠数,该重叠数由加速度卷波的相干长度来确定,δ是一次轨道运动后的相位差变化,ω是太阳自转的角速度。在光学中,上述方程是一个多缝干涉公式,对于较大的N,称为法布里–珀罗干涉公式。
在量子力学中根据Max Born的解释,|ψ|2等于找到电子的概率;在天体物理学方面,|ψ|2等于在天文尺度上平均找到一个核子(质子或中子)的概率,不管它是处在束缚态还是处在等离子体态,因为所有质量主要由核子质量构成,所以
(19)
根据光学的多缝干涉公式,重叠数N为
(20)
什么物质在太阳或地球中扮演“一个小波”的角色?我们选择地球表面海平面上的空气(含水蒸汽)作为“参考物质:一个小波”。因此,重叠数N由下式计算:
(21)
尽管今天太阳表面没有空气(含水蒸汽),但是不妨碍把它作为参考物质,太阳核心的最大密度为1.5e+5 kg/m3 [26],与地球上的海平面上的空气(含水蒸汽)密度1.29 kg/m3相比,太阳的加速度卷波重叠数N计算为N = 341。地核密度为5.53e+3 kg/m3,地球的加速度卷波重叠数N计算为N = 65。
对于太阳、地球和火星,其中心密度和参考物质密度如表2所示。

Table 2. Estimating the overlapping number N by comparing solid core to reference matter, regarding protons and neutrons as basis particles
表2. 通过比较固体核与参考物质,将质子和中子视为基本粒子,估算重叠数N
太阳赤道的自转角速度是ω = 2π/(25.05*24*3600),单位s−1。其质量1.9891e+30 (kg),半径6.95e+8 (m),平均密度1408 (kg/m3),极值加速度β = 2.961520e+10 (m/s2),太阳核心的最大密度为1.5e+5 kg/m3 [26],hM = 9.100745e+14 (m2/s)。根据N = 341,计算出来的太阳的物质分布|ψ|2在图4(b)中,它与太阳内部的一般描述吻合。
 (a)
(a)  (b)
(b)
Figure 4. (a) The head of the acceleration-roll wave may overlap with its tail. (b) The matter distribution |ψ|2 of the Sun has been calculated in radius direction
图4. (a) 加速度卷波的头部可与其尾部重叠。(b) 计算了半径方向上的太阳的物质分布|ψ|2
在图4(b)中,太阳半径计算值为r = 7e+8 (m),相对误差为0.72%,这表明太阳半径与太阳自转有强烈的依赖关系。
5. 地球的中心态与空间碎片分布
当我们考虑月球和地球时,我们也给地球指定一个量子数n = 0,并声称地球处于中心态。月球是地球唯一的天然卫星,如图5(a)所示。地球有五颗已知的准卫星,还需要考虑准卫星的近地点,如图5(b)所示,例如月球和2004_GU9等,但这一考虑需要进一步了解其五颗准卫星的行为 [29]。
 (a)
(a) 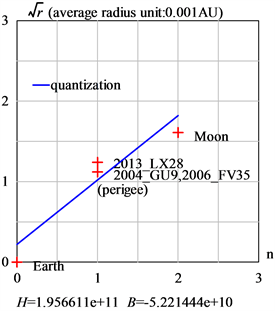 (b)
(b)
Figure 5. Orbital quantization for moon and quasi-satellites to the Earth, H = hM
图5. 月亮和地球准卫星的量子化轨道
将轨道量子化的线性回归关系应用于月球,我们得到图5(a),极值加速度为β = 1.377075e+14 (m/s2)。现在让我们来讨论地球的中心态,地球的自转角速度是ω = 2π/(24*3600),单位s−1。其质量为5.97237e24 (kg),半径为6.378e+6 (m),平均密度为5530 (kg/m3),极值加速度为β = 1.377075e14 (m/s2),常数hM = 1.956611e11 (m2/s)。
地球的中心态的加速度卷波的重叠数N = 65,计算出来的半径方向上的物质分布|ψ|2如图6(a)所示。赤道附近的自转周期为24小时,运动一圈的相位变化为
(22)
物质分布在中心有一个极大值,它在地球表面附近逐渐减小到零,然后上升出现几个次峰,然后再衰减到零。利用加速度卷波的干涉,计算出地球半径r = 6.4328e+6 (m),相对误差为0.86%。大气层上空的空间碎片有着复杂的演化过程 [16] [18],有着自身的速度
(23)
计算出了2000公里高度内大气中的干涉次峰,如图6(b)所示,这与空间碎片观测结果吻合很好 [16];890公里高度附近的峰值主要是由于2007年1月对风云-1C气象航天器的故意摧毁,而峰值集中在大约770公里高度是由2009年2月Iridium 33 (active) and Cosmos 2251 (derelict)通信航天器的意外碰撞造成的 [16]。2006年7月和2015年10月位于78˚N的非相干散射雷达EISCAT ESR的观测结果 [21] [22] [23] 分别如图6(c)和图6(d)所示。对次峰值的预测也与其他空间碎片观测结果吻合很好 [24] [25]。
 (a)
(a) 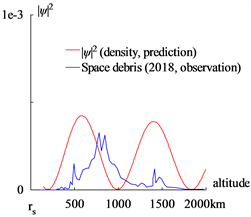 (b)
(b)  (c) (d)
(c) (d)
Figure 6. (a) The radius of the Earth is calculated out r = 6.4328e+6 (m) with a relative error 0.86% by the interference of its acceleration-roll wave; (b) The prediction of the space debris distribution up to 2000 km altitude; (c) The pace debris distribution in Jul. 2006, Joint observation based on the incoherent scattering radar EISCAT ESR located at 78˚N [21] ; (d) The space debris distribution in Oct. 2015, Joint observation based on the incoherent scattering radar EISCAT ESR located at 78˚N [21]
图6. (a) 通过其加速度卷波的干涉计算出地球半径r = 6.4328e+6 (m),相对误差为0.86%;(b) 2000公里高空内空间碎片分布预测;(c) 2006年7月的空间碎片分布,基于78˚N非相干散射雷达EISCAT ESR的联合观测 [21];(d) 2015年10月的空间碎片分布,基于78˚N非相干散射雷达EISCAT ESR的联合观测 [21]
6. 相干宽度和太阳黑子周期
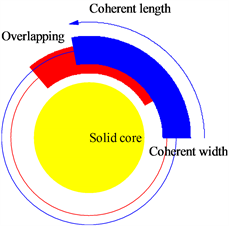
在量子力学中,波的相干长度经常被提及,但很少讨论波的相干宽度,因为后者不会成为电子、核子或光子的关心问题,而它却成为天体物理学的关心问题。分析观测数据告诉我们,在行星尺度上,加速度卷波的相干宽度可以延伸到1000公里甚至更多,如示意图7(a)所示,重叠可以在宽度方向上发生,从而为波的干涉带来新的特性。
在太阳对流区,相邻的对流阵列形成顶层气流、中层气体和底层气流,就像电磁学中的分子电流概念。顶层气流和中层气体之间存在明显的速度差,如图7(b)所示,其中它们的加速度卷波的干涉为
(24)
 (a)
(a)  (b)
(b)
Figure 7. (a) Illustration of overlapping in coherent width direction. (b) Convective rings at the equator, the speed difference causes a beat frequency
图7. (a) 相干宽度方向上的重叠示意图。(b) 赤道处的对流环,速度差导致拍频
这里C是耦合系数。它们的波动干涉会导致拍频现象
(25)
它们的速度计算如下
(26)
这里将Evershed流视为顶层气流的喷发,其速度有报导为大约6000 m/s [26],另外,用热力学方法在绝对温度5700 K估算v1 = 6200 m/s [29]。这里取v1 = 6100 m/s,这样计算出的它们的拍周期Tbeat是一个非常特别的值:10.93 (年),与太阳黑子周期值(平均11年)基本一致。
(27)
//C语言计算源码 [30]
double beta,H,M,r,rs,rot,v1,v2,K1,K2,T1,T2,T,Lamda,L;
int main(){beta=2.961520e10; H=SPEEDC*SPEEDC*SPEEDC/beta; M=1.9891E30; rs=6.95e8;
rot=2*PI/(25.05*24*3600);v1=rot*rs;K1=v1*v1/2; v2=6100; K2=v2*v2/2;
T2=2*PI*H/(K2-K1);T=T2/24*3600*365.2422; Lamda=2*PI*H/(v2-v1);L=2*PI*rs/Lamda;
printf(v1=%d, v2=%d, T=%.2f y,λ=%e, L=%f,v1,v2,T, Lamda,L);
}#v07=?>A
使用加速度卷波计算出拍周期,与11年平均值的相对误差为0.6%。这个拍的解释为:它是一个核子密度的上下波动驱动着太阳黑子周期的演化。拍频波长λbeat太长,无法观察,只有拍周期很容易观察到,如图8所示。
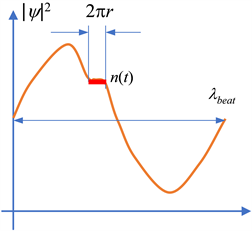
Figure 8. The equatorial circumference 2πr only occupies a little part of the beat wavelength, what we see is the expansion and contraction of the nucleon density
图8. 赤道圆周2πr只占拍频波长的一小部分,我们看到的是核子密度的膨胀和收缩
在上面的计算中,虽然这仅仅是一个计算模型,但太阳半径、太阳自转、太阳密度和类普朗克常数h之间存在明显的关联性。
7. 全球气候变化
可以从南极冰层样本中对过去80万年的温度和二氧化碳含量水平进行详细估计。那里的冰层已经堆积了一百多万年。通过钻入冰层,科学家可以检测气泡以发现古代的二氧化碳含量,并检测不同氧同位素的百分比以估计温度。这些详细的测量结果如图9所示 [27]。在这个时间范围内,地球温度随着冰川作用和二氧化碳水平的变化而升高或降低——震荡。

Figure 9. Earth’s temperature has gone up and down, with CO2 levels
图9. 地球温度随着二氧化碳水平的升高而升高或降低——震荡
Milankovitch周期描述了数千年来地球运动变化对气候的整体影响。这个词是以塞尔维亚地球物理学家和天文学家Milutin Milankovitch的名字命名的。20世纪20年代,他假设地球偏心率、轴向倾斜和进动的变化共同导致地球表面太阳辐射的年内和纬度分布的周期性变化,这种轨道扰动强烈影响了地球的气候模式。Joseph Adhemar, James Croll和其他人在19世纪提出了类似的天文假设,但验证很困难,因为当时没有可靠的证据,也不清楚哪些时期是重要的。近年来,人们研究了地球上几千年不变的物质(通过冰、岩石和深海沉积物岩芯获得),以表明地球气候的历史。尽管与Milankovitch假说大致一致,但该假说并未解释许多具体观察结果。
用ω表示地球固体核心的地球自转角速度,大气中的空气由于CO2杂质含量的变化,宏观上的空气角速度ωair与核心ω有一些不同。考虑转动惯量的恒定性,通过以下公式估计差异:
(28)
这里ρidle表示对地球空气自转变化没有贡献的CO2含量,即很长一段时间以来,其作用已被地球固体核心吸收了。在本文计算中,ρidle约为40 ppm。空气加速度卷波和地壳加速度卷波在它们的相干宽度内发生重叠干涉,如示意图10(a)所示,它们是
(29)
其中C是耦合系数,它们在相干宽度方向上的重叠干涉导致赤道半径r位置处的拍频现象
(30)
这样,CO2浓度的拍频波动为
(31)
在过去的800,000年中,空气中的平均CO2密度约为220 ppm,通过拟合观测数据我们知道耦合系数C = 0.136,因此很容易计算出CO2密度的拍周期为100.6千年,这一结果与南极冰测量结果一致,如图10(b)所示。拍频波长l太长,无法观察,只有拍周期很容易观察到。
 (a)
(a)  (b)
(b)
Figure 10. Earth’s temperature has gone up and down, with CO2 levels
图10. 地球温度随着二氧化碳水平的变化而升高或降低——震荡
假设全球变暖主要源于CO2杂质。大气压力由下式计算:
(32)
因为ρ和ρair不是常数,上述积分一般不能直接进行积分,海拔越高空气密度越低,Δρ和ρair比值越大。所以用杂质的堆叠系数γ常数来近似表示它们的变化,将通过实验来确定γ常数。设nair表示平均分子量为28.966的空气分子密度;
表示分子量为44的CO2分子密度。由杂质增加引起的压力变化为:
(33)
大气温度由下式计算:
(34)
按摩尔分数(即,按分子数),干燥空气含有78.08%氮气、20.95%氧气、0.93%氩气、0.0417%二氧化碳和少量其他气体 [31]。空气中还含有不同数量的水蒸气,在海平面平均约为1%,在整个大气中为0.4%。在拟合过去80万年的CO2密度后,通过拟合观测数据,堆叠系数取γ = 13.16。因此,通过上述方程预测全球变暖,如图11所示的红色曲线,结果与冰样本的观测结果一致。

Figure 11. Earth’s temperature has gone up and down, with CO2 levels
图11. 地球温度随着二氧化碳水平的升高而升高或降低——震荡
如图12所示,在过去的一个世纪里,二氧化碳水平上升了约30%。这一增长远远超过了过去1000万年的任何自然变化,因此大多数科学家将其归因于人类对化石燃料的燃烧增加。砍伐森林、开采煤炭和开采金属元素等,人类活动也减少了碳的储存场所。在同一时期,海洋和空气的平均温度上升了约0.8℃,这一现象被称为全球变暖。
在过去的一个世纪里,人类活动——各种采矿、提取化石燃料排放向大气中、飞机在空中飞行等等,都会造成大气的微小变化。堆叠系数仍取γ = 13.16,这个系数是从过去800,000年的数据中拟合获得的。因此,如图12所示,上述方程预测了全球变暖:在过去一个世纪,全球温度上升了约0.8℃,这一结果与教科书 [27] 中的估计值(0.8℃/百年)一致。
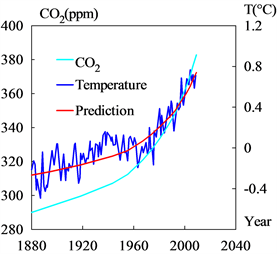
Figure 12. The prediction of global warming agrees well with the observation for the past century
图12. 全球变暖的预测与过去一个世纪的观测结果一致
8. 结论
与极值速度c类似,存在极值加速度b,任何物体的加速度都不能超过这个极限β。太阳系中的极值加速度β = 2.961520e+10 (m/s/s)。因为这个极值加速度是一个大数字,任何与β相关的效应都很容易测试,包括量子引力测试。本文提出了一种将极值加速度与量子理论联系起来的方法,提出了一种行星尺度的相对论物质波模型。这个模型计算出了太阳黑子周期为10.93年。拟合观测数据并计算出了全球气候变化的大尺度周期为100.6千年,与Milankovitch周期一致;估算出过去一个世纪全球气温上升了0.8℃。