1. 引言
在地震波法隧道超前地质预报数据采集过程中,炸药爆炸产生的空气振动波总会被地震波传感器所接收,在地震波信号记录中,空气振动波总会与有效的地震波信号相互重叠,从而对超前预报数据处理结果的真实性产生了影响 [1]。超前预报数据处理过程中怎样消除空气振动波,是提高数据信噪比及地质异常体准确定位的重要步骤 [2] [3] [4]。经过目前常用的带通滤波处理后发现,空气振动波并不能在单个频率域被有效地剔除。反射地震波隧道超前地质预报中非常依赖对数据的处理,通过对采集数据去噪,经过初至拾取、波场分离、反射波提取、偏移成像等最终确定反射界面的位置 [5],所以对反射波的识别极为重要,而声波的出现刚好与地震波反射信号重叠,这会对地震反射波的提取造成很大的困扰。
反射地震波隧道超前地质预报中,可将采集的数据看做非平稳信号,而在非平稳信号的处理中,时频变换是一种非常重要的信号分析方法 [6] [7]。炸药爆炸声波造成的检波器干扰在TSP数据记录中是比较复杂的,空气振波速度一般在344 m/s,而地壳中地震波平均速度达6200 m/s [8],超前预报中的地震波波速也往往在1500 m/s以上 [9],二者在波形记录时间上有时间差,且二者的频带范围也有差异,其主频略高于地震波的主频,频带大部分与地震波的频带相交,所以单单通过带通滤波是难以虑除的。声波对检波器的干扰过程是空气振动波进入对检波器的保护外套管、检波器钻孔内形成管内叠加振动以及空气振动波引起保护外套管的振动两者相互叠加形成的复杂干扰,干扰波没有一个有固定斜率的同相轴,故通过Radon变换、τ-p变换或FK变换难以去除 [10] [11] [12] [13] [14]。综上,利用时频域去噪方法比较适合对空气振动波的去除。
2. 时频域去噪方法原理
时频域去噪方法是将信号从时间维度变换到时间-频率维度,以便于进行与时间及频率有关的噪声去除方法,常用的时频域去噪方法有:短时傅里叶变换时频域去噪方法、小波变换时频域去噪方法、S变换时频域去噪方法等 [15] [16] [17]。短时傅里叶变换是在1946年由Gabor提出一种加时间窗口的傅里叶变换,将信号进行等时间、小间隔的分段,对每个小的时间间隔进行傅里叶变换,用以对传统的傅里叶变换加入时间性 [18] [19] [20]。小波变换是20世纪80年代后期发展起来的一门新兴的应用数学分支,近年有学者将小波变换引入到工程振动信号分析等领域中 [21] [22] [23]。S变换是1996年由地球物理学家Stockwell提出的一种给信号加特殊时窗的短时傅里叶变换表示法,即S变换从短时傅里叶变换发展而来,其窗口可随频率做适应性变化,Pinneger等人将S变换应用于含噪声的非平稳信号处理 [24] [25] [26] [27]。文章接下来会对短时傅里叶变换、小波变换及S变换这三种时频域提取算法进行详细介绍,对比其在TSP数据处理中对空气振动波干扰的滤除效果,通过对实际采集的TSP数据进行处理,分析了短时傅里叶变换、小波变换以及S变换的时频分析特性,与短时傅里叶变换、小波变换两种时频分析方法进行对比,分析了S变换的特点。
2.1. 短时傅里叶变换
短时傅里叶变换原理,见图1:

Figure 1. Theory of Short Time Fourier Transform
图1. 短时傅里叶变换原理
(1)
式(1)中,t表示时间,s(t)为时域信号,
,f表示频率,
,“
”号表示内积,“*”号表示复共轭 [28]。
根据复变函数欧拉公式
[29],傅里叶变换可表示为:
(2)
傅里叶逆变换可表示为:
(3)
短时傅里叶变换的表达式为:
(4)
从定义式(4)可以看出,h(t)是一个“滑动的”窗口,当t发生变化时,它随着t的变化而沿着信号s(z)滑动 [30]。由此利用窗函数把整段信号先分解成一系列近似平稳的“小片段”,再对每一个不同的“小片段”进行傅里叶变换得到对应的频谱,这些频谱的总和即为信号的时频分布,即“频谱图”,其中,
为角频率 [31] [32]。短时傅里叶变换的逆变换表达式为:
(5)
2.2. 小波变换
首先,若函数
满足条件:
(6)
且能保证能量单位化
(7)
称函数
为母小波或基小波。式(7)中,a称为伸缩因子或尺度因子,用来调整子波频率的覆盖范围;b称为平移因子,用来调整子波的时域位置 [22];一般地:
(8)
称为母小波
生成的连续小波函数,它是依赖于参数a,b的小波基函数,可表示一类由同一基本小波经过伸缩、平移后得到的函数族 [31] [32]。
若
平方可积并且其傅里叶变换
满足连续小波变换的允许性条件:
(9)
则信号s(t)在尺度a、位置b的连续小波变换定义为:
(10)
这里,
(11)
根据Parseval恒等式 [33] [34]
(12)
若母小波函数
满足公式(12),那么有:
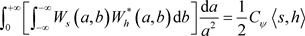 (13)
(13)
则连续小波变换的逆变换为:
(14)
2.3. S变换
在短时傅里叶变换中,根据信号分析的不确定原理,窗函数为高斯类函数时,窗口面积达到最小 [35]。结合短时傅里叶变换公式,S变换可表示为
的内积形式 [36],即(图2)
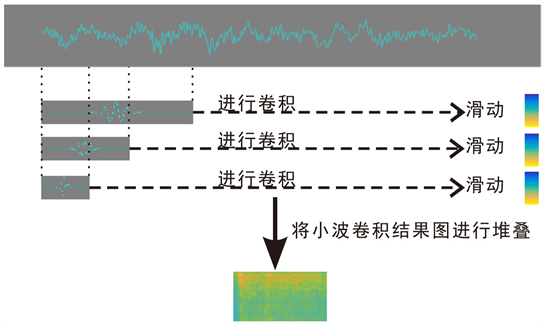
Figure 2. Schematic diagram of wavelet transform
图2. 小波变换原理图
(15)
可以得出,S变换与傅里叶变换之间有关系 [37] [38]
(16)
根据短时傅里叶变换在时频域的相互转化,可得到S变换在频域的表示:
(17)
其中,
与f是相同的意义,H(y)表示S变换窗函数h(t)的傅里叶变换 [39]。由此可得出无损S变换逆变换(IST)的表达式为:
(18)
3. 实际数据处理与分析
TSP原始数据见图3(a),从图中可知,空气振动波的干扰非常强烈,大部分的地震反射波信号被覆盖在空气振动波的干扰中,该数据在2020年9月25日采集于兰张三四线铁路古浪段某隧道。在地震记录中声波干扰部分往往表现为干扰时间长、振幅大、时间长的特点 [40],而干扰波初至的连线刚好为344 m/s,这表明检波器在接受到空气振动波干扰的时候,同时也接收了由空气振动波引起的其他干扰振动(图3(b))。
对该隧道采集的TSP原始地震信号进行短时傅里叶变换、小波变换及S变换的时频域提取及声波去噪处理,并进行结果分析及算法特点介绍。
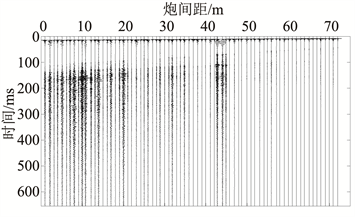
 (a) 兰张三四线铁路古浪段某隧道TSP记录 (b) 地震记录频谱
(a) 兰张三四线铁路古浪段某隧道TSP记录 (b) 地震记录频谱
Figure 3. Seismic Record (a) and Spectrum (b) of Tunnel in Gulang of Lanzhang Railway
图3. 兰张三四线铁路古浪段隧道地震记录(a)与频谱(b)
3.1. 短时傅里叶变换
对原始TSP数据进行短时傅里叶变换计算时,需要提前指定参数,根据信号的特点,采用Hamming窗;矩形窗的基波各振幅都比较尖,其对应的频谱中频宽较宽且主频分散,主要是矩形窗的主瓣较窄,对频率高的数据部分有较好的分辨率,但其旁瓣增益较高,基波相邻谐波之间的干扰严重,容易发生频率泄露,而Hamming窗则无明显的频率泄露 [41]。每个窗口的长度设为300个采样点;每相邻两个窗口的重叠率为窗口长度的一半;每个窗口的FFT采样点数为与窗口长度最接近的2的N次方的数,参数指定完成后,对数据进行短时傅里叶变换,提取出时频域数据,见图4。
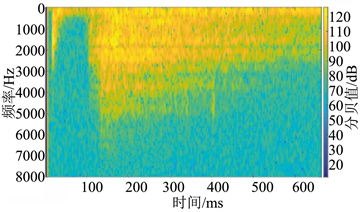
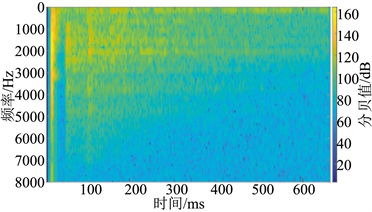 (a) 第10道数据短时傅里叶变换后的时频图 (b) 第70道数据短时傅里叶变换后的时频图
(a) 第10道数据短时傅里叶变换后的时频图 (b) 第70道数据短时傅里叶变换后的时频图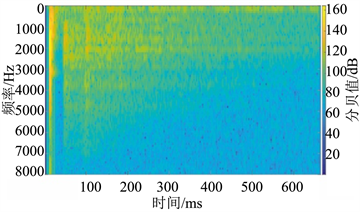
 (c) 全部道数据短时傅里叶变换后的时频图 (d) 经过短时傅里叶变换去噪后的地震记录图
(c) 全部道数据短时傅里叶变换后的时频图 (d) 经过短时傅里叶变换去噪后的地震记录图
Figure 4. Time Spectrum and Seismic Record of Short time Fourier Transform
图4. 短时傅里叶变换处理前后的地震记录图
通过原始地震信号图3(a)可知:第10道的声波干扰较强,其对应的时频图见图4(a);第70道的声波干扰非常弱,其对应的时频图见图4(b);对比图4中的(a)、(b)可以看出短时傅里叶变换时频分析的结果符合该原始地震信号声波干扰特征。对原始地震信号的全部道进行短时傅里叶变换时频分析结果见图4(c),对时间靠后的高频信号进行去除后,在进行逆短时傅里叶变换可得到去噪后的地震信号见图4(d),初至地震波被有效的保留下来,而声波干扰部分的高频信号被去除,取得有较好的去噪效果。
短时傅里叶变换克服了傅里叶变换对非平稳信号分析时,没有时间性的缺陷,算法增加了窗函数后,就实现了时间–频率分析,算法简单实用,降低了初学者研究时频分析算法时的门槛。
短时傅里叶变换不足之处在于,对于局部变化较大的非平稳信号处理效果较差。短时傅里叶变换使用的窗函数是固定长度的,计算时其形状就不再改变,即分辨率也就确定了。如果要改变分辨率,则需要重新选择窗函数,不能兼顾频率与时间分辨率的需求。受到测不准原理的限制,短时傅里叶变换窗函数的时间与频率分辨率不能同时达到最优 [7]。
3.2. 小波变换
小波变换必须通过小波基的运算进行实现,可以视为将短时傅里叶变换无限长的三角函数基换成了有限长的会衰减的小波基,其能量有限,都集中在某一点附近,且积分的值为零 [42]。通过公式(8)可知,可以通过小波变换的尺度a得到频率,通过平移量b得到时间,故可提取出信号的时频谱。选用复的morlet小波基,其带宽参数和中心频率取得越大,时频图上反映的时频聚集性越好,选择尺度为512,通过小波变换变换的时频分析可得的图5。
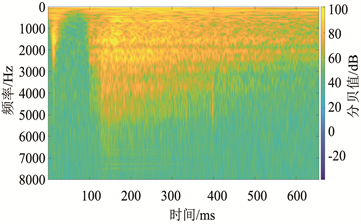
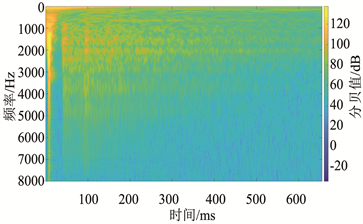 (a) 第10道数据小波变换后的时频图 (b) 第70道数据小波变换后的时频图
(a) 第10道数据小波变换后的时频图 (b) 第70道数据小波变换后的时频图
 (c) 全部道TSP数据小波变换叠加时频图 (d) 小波变换去噪后的地震记录图
(c) 全部道TSP数据小波变换叠加时频图 (d) 小波变换去噪后的地震记录图
Figure 5. Time Spectrum and Seismic Record of Wavelet Transform
图5. 小波变换处理前后的地震记录图
对比图5中的(a)、(b)可以看出小波变换时频分析的结果符合该原始地震信号声波干扰特征。对原始地震信号的全部道进行小波变换时频分析结果见图5(c),去除噪声信号后,进行逆小波变换可得到图5(d),初至地震波被有效的保留下来,而声波干扰部分的高频信号被去除,取得有良好的声波去噪效果。
小波变换具有多分辨特性,通过适当地选择尺度因子、平移因子及基本小波,就可以使小波变换在时域和频域都具有较好的分辨能力 [21]。小波变换的原理与傅里叶变换在无穷区间上对相互正交的三角函数信号和原信号分段进行积分的原理是类似的,但小波基函数可根据信号特征构造,这为信号和噪声的分离以及分频处理带来了很大的方便 [22]。小波变换的缺点在于将时间信号分解到时间尺度域,而非时频域,尺度并不是真实的频率。除此之外,小波变换的自适应性是建立在需要选定一个适合原始数据的小波基函数,这两点可能会导致小波变换在作信号处理时得到较低的时频分辨率 [23]。
3.3. S变换
进行S变换计算时,需要提前定义一个可进行伸缩与平移的高斯窗函数作为S变换的唯一基函数,其余的计算步骤与短时傅里叶变换、小波变换中的一些步骤一致。通过对给定的实际TSP地震数据进行处理,可以得到图6中(a)、(b)、(c)图,去噪后的地震记录见图6(d),可知S变换拥有很好的时频提取效果及噪声去除效果。

 (a) 第10道TSP数据S变换后的时频图 (b) 第70道TSP数据S变换后的时频图
(a) 第10道TSP数据S变换后的时频图 (b) 第70道TSP数据S变换后的时频图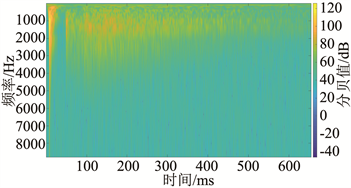
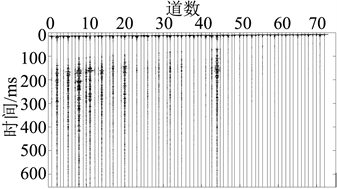 (c) 全部道TSP数据S变换叠加时频图 (d) 经过S变换去噪后的地震记录图
(c) 全部道TSP数据S变换叠加时频图 (d) 经过S变换去噪后的地震记录图
Figure 6. Time Spectrum and Seismic Record of S-transform
图6. S变换处理前后的地震记录图
S变换算法是对小波变换的一种相位修正算法,其分辨率可随信号的实际频率而变化,且具有明确频率意义的。其缺点时当信号的频率较高时,S变换的频宽窗口就比较大,而时间窗口就比较小,从而导致了频率分辨率较低而时间分辨率较高。
4. 结论
时频域去噪方法是处理地震反射波法隧道地质超前预报声波干扰的重要工具。该方法将信号分解到时间–频率域,突出了信号的频谱随时间的变化规律。通过对实际采集地震波数据对比分析,结果表明,时频域去噪三种方法中由于S变换的时频窗口随频率自适应调整,S变换在隧道超前地质预报时变滤波中效果更具精度优势。