1. 引言
我国是世界上最大的烟草生产国,烟叶产量、卷烟产量与烟草行业从业人数均位列世界第一,烟草行业作为我国财政收入的一大来源,近年行业竞争愈发激烈。在卷烟生产中,工艺是关键,质量是核心,制丝流程的工艺水平成为诸多卷烟企业一较高下的决胜因素,对该流程的工艺参数分析将为工艺技术和生产品质的提升提供有力支持。
经过调研发现,烟厂坚持致力于引入新设备,新技术,改进过程质量管理系统,追求更高的产品质量,但实际应用效果却始终没有达到最优,海量的加工过程数据没有得到充分的处理和分析、统计过程控制与诊断(Statistical Process Control and Diagnosis, SPCD)理论没有落到实处、质量评价与分析过程仍主要依靠人为经验判断等,烟草的整个加工过程中质量损失较大、产品内在稳定性较低等一些问题有待改进。
在卷烟的三大加工工艺中,烟叶制丝流程是至关重要的一环,该流程产物的质量好坏决定了卷烟产品的品质高低。而制丝工艺主要包含松散回潮、加料、切烘等子过程,是一个多耦合、自相关、非线性、多干扰的复杂过程,对于该流程的参数分析和优化已经成为了一类具有挑战性的课题。因此,从制丝流水线参数数据出发的关联分析有助于探寻各阶段参数的关联关系,进而实现各阶段的参数优化,具有较高的研究价值与现实意义。
目前,有不少国内学者从不同角度切入该课题,结合不同的统计方法,尝试建立模型评估优化制丝过程的工艺参数。赵蓉蓉 [1] 和鲁宇童等人 [2] 采用正交试验设计方法,探究分析了松散回潮、加料和烘丝工序的工艺参数对叶丝结构、烟气、烟支的物理特性和感官质量的影响,并用直观分析、方差分析和综合平衡法进行参数的优化分析。赵佳成等人 [3] 从切丝工艺入手,对不同切丝宽度条件下的成品烟丝结构数据进行方差分析,之后利用灰色关联度分析法对其烟丝结构分布的稳定性进行综合评价。张刘渲楠 [4] 和雷振等人 [5] 利用烘丝机加工过程中的不同工艺参数的数据,通过Pearson相关性分析和主成分分析探究了烘丝机工艺参数的数据特征。何邦华等人 [6] 选取制丝工艺中5个关键参数进行均匀试验设计,之后根据各试验组检测的烟丝填充值、整丝率和碎丝率对工艺参数和质量指标进行BP神经网络建模,预测不同参数组合对应的烟丝物理质量。
现阶段针对制丝工艺参数的研究大多从松散回潮、加料、切烘中的某一个阶段出发,探讨该阶段内参数调整对制丝流程产品质量的影响,即单一阶段的关联发掘。然而,对于三阶段串联后各阶段间参数关联关系的探究则并不多见。而神经网络等机器学习方法建模虽然可以有很高的预测精度,但是缺乏对工艺过程的机理分析,缺乏实际指导意义。
简言之,在这一课题上,诸多学者从不同方向进行了探索性研究,提出了许多可行的制丝流程优化思路。目前,仍有许多方法和模型还未加以尝试,这一领域的研究依然面临着不小的挑战。
结构方程模型(Structural equation modeling, SEM)是一种融合了因素分析和路径分析的多元统计技术。自Joreskog和Wiley (1973)提出以来,众多学者不断深入挖掘这一模型的可能性,SEM分析逐渐成为当今以社会科学和心理学为代表的诸多领域中极为重要的一种统计方法并广泛用于实证研究中。黄秋杰 [7] 通过结构方程模型分析了中国财险公司的盈利能力,发现具有直接影响的是企业规模,并提出了提高营利能力的相关举措。李新杰等 [8] 利用SEM模型对中部六省的数据展开研究,评估了新生代农民工的心能、智能、体能和技能四个人力资源能力。申珅 [9] 从形成性偏最小二乘结构方程模型(简称PLS-SEM)出发,探究了烟草种植、税收及消费等因素对烟草生产的影响,并给出有针对性的政策建议。
总体来说,SEM分析经过数十年的发展,已具备较为坚实完善的理论体系,得到了广大研究者的认可和广泛应用。与其它研究相比,结构方程模型除了能够计算评估各指标间的关联程度,还能将各阶段参数进行串联,刻画完整的工艺流程以及其中的指标关系,并进行相关统计计算,是目前比较理想的处理研究数据的模型。
因此,本研究基于某烟厂制丝流程流水线上的工艺参数数据展开,从数据分析的角度出发,数据进行清洗后,将研究重点主要集中在松散回潮工序、加料工序和烘丝工序的工艺参数关联关系发掘,通过建立形成性PLS-SEM探索各工艺参数对制丝流程的主要品质衡量指标填充值的影响,尝试在现有工艺经验的基础上发掘制丝流程中各阶段工艺参数与输出指标的多重关联性。对这些指标影响显著的阶段和显著的工艺参数给出可能的调整策略,为实际生产过程中工艺参数的调整优化给出可行建议。
2. 数据
选取上海卷烟厂中华牌号制丝工艺线为研究对象,收集了2019年1月1日至2020年9月27日期间包括批次号、日期以及制丝工艺过程中松散回潮、加料和切烘三个阶段各类工艺参数共121个变量在内无缺失值的3064条生产记录。
考虑到原数据集内共121个工艺参数变量,直接使用原数据集进行建模分析,变量过多可能导致模型运算量过大,很多变量间的相关关系也会导致建模效果不稳健。基于此,在不损失过多信息的前提下必须精简建模的变量和数据集。删除描述批次号和日期时间的变量;计算数据的样本方差值,删除部分在生产过程中取值基本固定不变(变量标准化后的样本方差值 ≤ 0.05)的变量。结合异常值检测,在删除变量的异常值后,绘制变量的分布图,通过分布的卡方拟合优度删除分布情况较差的变量。对3064条工艺过程记录进行清洗和变量初步筛选后,依照制丝工艺过程中松散回潮、加料和切烘的工艺流程阶段,依次讨论各阶段变量间的(多重)共线性情况,通过计算变量Pearson相关系数和方差膨胀因子(VIF)值对变量间的(多重)共线性进行评估,最终确定各阶段的观察变量(具体见表1)。
Diamantopoulos和Siguaw等人 [10] 2006年指出,为保证建模效果保持在较高水平,最好将SEM模型中的观察变量间的VIF控制在3.3以下。经验证可得数据集中所有自变量指标的VIF值都小于3.3。三个阶段的变量的相关系数热力图如下图1,相关系数最大值不超过0.41。
3. 方法与模型
一个完整的SEM包含测量模型和结构模型两部分,前者用于刻画观察变量与潜在变量之间的关联情况,后者用于描述潜在变量之间的关联情况,其中测量模型又可以分为反映性模型(reflective model)与
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 1. Diagram of variable correlation coefficient
图1. 变量相关系数图
形成性模型(formative model)两种不同情形.两种测量模型的主要差异在于观察变量和潜在变量之间的因果关系不同。对于反映性测量模型,潜在变量是“因”,观察变量是“果”,观察变量可以视为对应潜在变量含义的一种表现,同一潜在变量的观察变量之间具有高相关性且可互相替代;形成性测量模型则正相反,观察变量是“因”,潜在变量是“果”,观察变量解释对应潜在变量的一部分信息,进而同一潜在变量的观察变量之间不相关也无法互相替代。
另一方面,根据估计关联性时使用的算法不同,SEM可分为基于变量间协方差结构方程模型(Covariance-Based SEM,简称CB-SEM)与PLS-SEM两类模型。CB-SEM是基于变量间的协方差矩阵展开、使用极大似然估计法进行关联性估计的模型,更偏向于对理论的检验性分析,对于数据量和数据分布也有较高要求;PLS-SEM则从变量的方差出发,使用以最小二乘回归为基础的统计方法对变量之间的关联性进行分析,在发掘数据间关联结构和预测方面有较好表现,对于数据量和分布的要求也相对较低.一般情况下,对于模型复杂度较高、涉及形成性构念、数据分布非正态或小样本的情形下,PLS-SEM具有更好表现。
本研究中,考虑到潜在变量所包含的信息为各观察变量的结合,即观察变量是“因”,潜在变量是“果”,另一方面,本研究所使用的部分数据分布非正态,且研究属于探索式研究,所以选择形成性PLS-SEM作为研究方法。
模型的解释能力由R2、外部权重、外部因子载荷来反映,通过路径系数及Bootstrapping检验结果反映模型变量间的因果关系。
4. 结果与分析
本研究在数据清洗的基础上,使用Smart PLS 3软件(3.2.9版本软件)以填充值为输出指标,建立了形成性PLS-SEM。采用结构方程模型探究了制丝过程中松散回潮、加料和切烘三个阶段的输出指标与最终输出指标的关联性;用测量模型发掘了各阶段的观察变量与潜在变量之间的关系。考虑到各阶段的观察变量数量较多,因此本研究使用重复指标方法,将各阶段输出指标设置为二阶外生潜在变量,在其下分别定义“温度”和“湿度”两个一阶外生潜在变量,用以具体探究各观察变量的作用情况。图2示意了本研究中使用的结构方程模型,其中潜在变量用圆圈表示,观察变量用矩形框表示。

Figure 2. Diagram of structural equation model path
图2. 研究用结构方程模型路径示意图
各阶段相关联的观察变量与潜在变量由表1给出。并给出了各阶段观察变量在一阶外生潜在变量和二阶外生潜在变量下的VIF值。从表中可知所有观察变量的VIF均小于3.3,可以认为观察变量间基本不存在(多重)共线性带来的影响,这一结论与数据清洗阶段的讨论与处理结果是一致的。
通过计算可得,对于最终输出指标填充值,模型
与
均为0.688,参照Chin [11] 提出的结构方程模型
评估标准,这一数值大于0.67,因此可以认为在现有模型中,“预配含水率”、“加料后含水率”与“切烘阶段输出”三个外生潜在变量对于最终输出指标填充值的解释度与预测精度都达到了较高水平。此外,作为对
的补充说明,本研究计算了填充值这一指标的预测相关度,计算结果
,也反映了现阶段建立的是一个能够较好预测填充值的模型。
基于良好的预测精度与预测相关性,本研究在PLS-SEM的基础上,利用原数据对填充值进行预测,从10折交叉验证的预测结果可以看到,对于填充值的预测结果中,均方根误差RMSE = 0.058与平均绝对误差MAE = 0.046都较低,可以认为本研究构建的形成性PLS-SEM对于填充值表现出高模型解释度以及高预测精度。图3给出了填充值模型路径图,图中包含各观察变量的外部权重、潜在变量的判定系数
以及潜在变量间的路径系数。
观察变量在一、二阶外生潜在变量下的外部权重以及显著性检验的结果如表2所示。
可以看到,一、二阶外生潜在变量下外部权重均不小于0.1且显著,这一类变量包括“松散回潮工艺气体温度”、“松散蒸汽温度”、“松散回潮加水比例”、“加料机排潮风温度”、“加料温度”、“切烘温度等级”、“切烘HT蒸汽温度切温”、“进风风速”等。这些指标反映了对应外生潜在变量较多信息,同时也具有较高的显著性。
在松散回潮阶段,“松散回潮工艺气体温度”与“松散回潮加水比例”分别是该阶段中对一阶外生潜在变量“温度”和“湿度”影响最显著的两个变量,其中后者对于二阶外生潜在变量“预配含水率”的影响最显著;在加料阶段中,对于“温度”和“湿度”影响最显著的分别是“加料温度”和“加料HT蒸汽压力等级”两个变量,“加料温度”对二阶外生潜在变量“加料后含水率”的影响更显著;切烘阶段,“切烘HT蒸汽温度与切烘温度温差”和“进风风速”在各自构成的一阶外生潜在变量下最显著,前者对“切烘阶段输出”的贡献更显著。
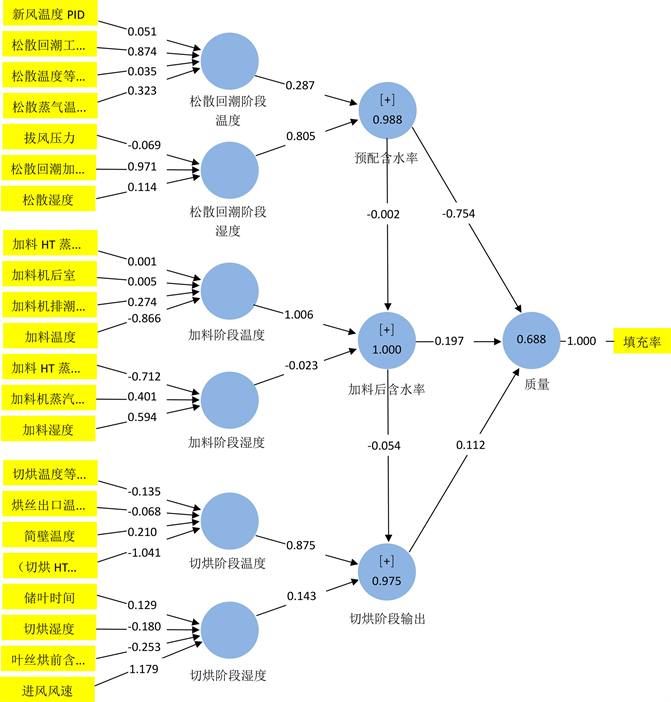
Figure 3. Path analysis model of variable filling value
图3. 填充值路径分析模型

Table 2. Weighted value and significant test of variables
表2. 观察变量的权重值及显著性检验
**表示高度显著。

Table 3. Path coefficients of significant variables and Bootstrapping analysis
表3. 各显著变量的路径系数和Boostrapping分析结果
表3列出了潜在变量之间的路径系数以及路径系数的显著性检验结果,反映了各潜在变量之间的影响关系。在结构模型中,各路径的潜在变量之间的VIF均小于3.3,因此认为潜在变量之间基本不存在(多重)共线性,结构模型后续各项分析与检验不会受到影响。
又,全部路径的路径系数p值 < 0.05,说明这些路径上的影响关系都是显著的。“加料阶段温度→加料后含水率”这一路径的路径系数高达1.006。可以认为在以填充值作为最终输出指标的结构方程模型中,“加料阶段温度”对“加料后含水率”的影响是绝对显著的,即在加料流程中,温度对于这一阶段的输出品质起决定性作用。
此外,“松散回潮阶段湿度”和“切烘阶段温度”分别对“预配含水率”和“切烘阶段输出”的影响更为显著,即湿度与温度分别是决定松散回潮阶段和切烘阶段输出品质的关键因素。在松散回潮、加料和切烘三个阶段输出指标中,松散回潮阶段的输出品质对填充值造成的影响更大,体现在“预配含水率”对于填充值的影响更加显著,二者之间存在较强的负相关关系,即“预配含水率”每产生单位变化,填充值随之产生−0.754单位变化。
综上测量模型和结构模型分析可得,填充值的显著影响路径依次为松散回潮加水比例→松散回潮阶段湿度→预配含水率→填充值。
5. 结论
本研究对某烟厂制丝流水线上获得的工艺参数数据进行筛选清洗后,以填充值为最终输出指标建立了偏最小二乘法测度下的形成性结构方程模型,发掘松散回潮、加料和切烘阶段对于最终输出指标具有显著影响的工艺阶段与具体参数。与其它研究相比,本研究不仅仅关注某一阶段的工艺参数带来的影响,而是着眼于制丝流程多阶段串联后显著关联关系的发掘。模型评估结果表明,本研究建立的结构方程模型对于填充值具有较好的模型解释度/预测精度。松散回潮阶段的影响相较于其它阶段更显著,表现为负向影响(−0.754)。具体而言,该阶段显著工艺参数为“松散回潮加水比例”。因此,生产过程中对于制丝流程产品的填充值的提升有必要重点关注松散回潮阶段的湿度参数的调整。总体而言,湿度的影响要强于温度,生产过程中需要更多关注湿度参数的调整。
基金项目
受上海市浦江人才计划资助项目(项目编号2019PJD055)和高等学校大学数学教学研究与发展中心项目(项目编号CMC20210411)资助。