1. 引言
随着化石能源的日益枯竭和对环境保护的日益重视,可再生资源规模化利用将在未来的电力行业中发挥举足轻重的作用,其中风力发电因具有环境友好、应用广泛、建设周期短且规模效益好等优点而成为发展最快的新型能源 [1]。但是风能是一种天然能源,具有间歇性和波动性,将风力发电并网后给系统的功率、电压和稳定性带来诸多不利影响,难以满足电力系统稳定的供电需求,将储能技术引入风力发电系统,调节储能系统使其快速有效地改善风电场的输出、平滑输出功率,可以将并网的风电出力波动限制在允许范围内,很好地解决了风电大规模并网的问题。
大规模风电并网和规模化储能利用将会成为未来电网的主要特征之一 [2]。如何利用规模化储能技术有效改善风电系统的运行特性、提高风电电力系统的安全稳定性,将会是未来储能广泛应用及大规模风电并网消纳进程中的一个重要课题,也是一个亟需研究解决的问题。
风力发电因其具有资源分布广泛、存储容量大、环境友好、开发技术成熟等特点,已经成为全球最受欢迎的可再生能源之一,是各国未来能源战略中的重要组成部分 [3]。大规模发展风力发电已经成为了全球能源开发中的一种主流趋势,如何低成本且有效地利用风力发电和储能系统供电,设计可靠的供电平衡策略是各国的电力系统要攻坚的重要内容。
2. 问题提出
下面以高比例风电电力系统为例,探究“供给侧”低碳化转型对电力系统运行经济性、可靠性影响。
待研究系统包含火电、风电、储能和负荷,火电机组3台、装机容量1050 MW;某日风电、负荷归一化功率(1.0 p.u.风电对应其装机容量,1.0 p.u.负荷对应最大负荷功率),风电渗透率(最大风电功率与最大负荷功率之比)递增可能造成系统弃风、失负荷,影响系统功率平衡。
定义:系统单位供电成本 = 系统发电总成本/系统总负荷电量,发电总成本 = 火电成本 + 风电成本 + 储能成本 + 弃风损失 + 失负荷损失,其中:
1) 火电成本包括运行成本、碳捕集成本,其中火电运行成本由运行维护成本和发电煤耗成本构成,发电煤耗与其出力关系:
,F为机组煤耗量(kg/h),p为机组出力/MW;运行维护成本按照0.5倍煤耗成本考虑,碳捕集成本取决于碳排放量及碳捕集单价,火电机组相关参数见表1,电煤价格为700元/t。

Table 1. Related parameters of thermal power unit
表1. 火电机组相关参数
2) 风电成本仅考虑运维成本,相关参数见表2。

Table 2. Wind power operation cost parameters
表2. 风电运行成本参数
3) 储能成本由投资成本、运维成本构成,相关参数见表3。注:在计算每天成本时,需将投资成本平摊至每天,即平均每天投资成本 = 总投资成本/运行年限/365天。

Table 3. Energy storage cost parameter
表3. 储能成本参数
4) 弃风损失按0.3元/kWh计算,失负荷损失按8元/kWh计算。
假设系统日负荷功率最大值900 MW,单位碳捕集成本为100元/t,摄动风电渗透率,分析计算以下问题:
一、在无风电和储能系统接入,并且三个不同参数的火力发电机组以最小成本平衡供电时,绘制各机组日发电计划曲线,计算出系统单位供电成本为多少?
二、当用风电装机300 MW替代火力发电机组3时,电力系统功率平衡将会如何变化?所产生的弃风电量为多少?系统单位供电成本多大?在此场景下,为减少弃风损失并且又不失负荷的情况下,风电接入装机容量最多可以降低多少?
三、考虑储能系统的接入,为不失负荷,需要配置的最小储能容量将是多少(储能充放电效率90%)?如果考虑储能成本(取60元/t)、单位碳捕捉成本,此时系统单位供电成本为多大?
3. 问题分析
3.1. 问题一的分析
本文利用非线性优化模型 [4],根据一天的用电供需情况,得出三台火电机组的最佳平衡策略。从而绘制出各机组日发电计划曲线,计算出各机组的供电成本。
3.2. 问题二的分析
用风电装机代替火电机组3,整个系统的额定功率额将会上升,但装机容量不变,这样会导致系统供电平衡稳定性下降。若已知当天的风力资源,弃风电量即为超出当天某时刻供需的电量。在问题一中火电成本的基础上,当两个机组的最低功率总和加上风力资源大于用户端的供需,必定会出现弃风损失,此时成本就为最小成本。若两个机组的最低功率总和加上风力资源小于用户端的供需,是提高两火电机组的功率满足用户端的供需,还是无视用户端的供需,增加弃负荷成本,选取哪种最优策略则由两种情况所需的成本更低来决定。
3.3. 问题三的分析
在供电需求和风力资源已知,且不失负荷的情况下,考虑储能系统的接入,那么在面对满足用户端的供需时有两种选择:一是按照问题二的做法,不考虑储能,在风力资源不足时,通过提高火电机组的功率来满足用户端的供需。二是在发生弃风时,将弃风电量储存到储能设备中,之后再通过储能系统来提供给用户端使用。通过非线性优化求出最优策略,而一天中储能设备的储电最大数值即为可配置的最小储能容量。
4. 符号说明
用于对解决问题一、问题二和问题三所建立的模型中的一些参量符号的说明解释,说明其具体的实际意义。
5. 模型建立与求解(模型中符号说明见表4)
5.1. 问题一模型的建立与求解
5.1.1. 模型的建立
本文利用非线性优化模型,根据一天的用电供需情况,得出三台火电机组的最佳平衡策略。从而绘制出各机组日发电计划曲线,计算出各机组的供电成本,具体见表5。
由题可得:
(1)
(2)
(3)
(4)
基于非线性规划,得:
5.1.2. 模型的求解
解得P1、P2、P3,将其代入下式:
(5)
(6)
(7)
(8)
(9)

Table 5. Calculation results of question one
表5. 问题一的计算结果
分别画出P1、P2、P3与t的对应关系于图1:
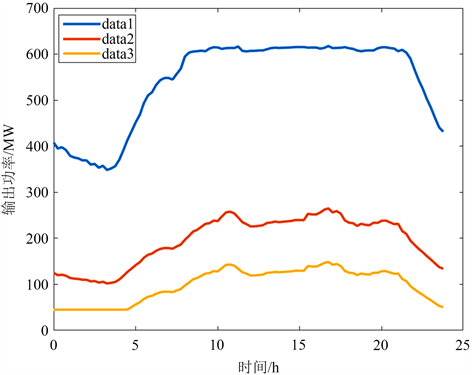
Figure 1. Daily power generation schedule curve chart of thermal power units
图1. 各火电机组日发电计划曲线图
5.2. 问题二模型的建立与求解
5.2.1. 模型的建立
由题可得:
(10)
当
时,必会有弃风损失,无失负荷损失,则基于非线性规划,得:
当
时,无弃风损失,可能会有失负荷损失,此时
,则基于非线性规划,得:
5.2.2. 模型的求解
问题1时,
,问题2时,
,
,则风电装机300 MW替代火电机组3时,系统功率平衡降低。给出风力资源的最大值为300 MW,风电装机为300 MW,故在此场景下,为减少弃风又不失负荷,风电接入装机容量可以降低0 MW,如表6所示。
(11)
(12)
(13)
(14)
(15)
(16)
(17)

Table 6. Calculation results of question two
表6. 问题二的计算结果
5.3. 问题三模型的建立与求解
5.3.1. 模型的建立
基于非线性规划,得:
其中:
(18)
(19)
5.3.2. 模型的求解
解得P1、P2、P3,将其代入(6)、(7)、(8)式以及下式(结果见表7):
(20)
(21)
(22)
(23)
(24)
(25)

Table 7. Calculation results of question three
表7. 问题三的计算结果
6. 模型评价
6.1. 模型的优点
模型思路简单清晰,文字注释完整且实用性较高,紧扣当今时代发展的趋势,能较好地模拟出一些理想的情况,并提供合理的最优化策略。
该模型适用范围广,可运用到多种发电模式且产生的误差在一个可接受的范围内。
模型在一定程度上准确且巧妙地描述了问题,且对其进行了相当地简化,易于理解操作。
6.2. 模型的缺点
该模型未考虑到国家政策的调控与自然灾害的影响等实际情况,结果容易受其改变。
模型涉及的因素较多,不能对其进行全面的考虑,造成与实际有一定的不相符之处。
7. 结语
本文利用非线性优化模型及利用微积分方法,根据一天的用电供需情况,得出火电机组的最佳平衡策略,并计算出各机组的供电成本。
用风电装机代替火电机组,整个系统的额定功率额将会上升,但装机容量不变,这样会导致系统供电平衡稳定性下降。本文通过比较两个机组的最低功率总和加上风力资源与用户端需求的大小关系,可以得出,当前者大于后者会出现弃风损失,此时成本即为最小成本。当前者不超过后者,会出现两种选择:一是提高火电机组的功率来满足用户端的供需,二是无视用户端的供需,增加弃负荷成本,选取哪种最优策略则由两种选择中所需的成本更低来决定。
在供电需求和风力资源已知,为不失负荷的情况下,考虑储能系统的接入,那么在面对满足用户端的供需时有两种选择:一是不考虑储能,在风力资源不足时,通过提高火电机组的功率来满足用户端的供需。二是在发生弃风时,将弃风电量储存到储能设备中,之后再通过储能系统来提供给用户端使用。通过非线性优化求出最优策略,从而计算出一天中储能设备的储能电量最大值即为最优储能容量。
基金项目
湖南省大学生创新创业训练计划项目(3501)。
NOTES
*通讯作者。