考虑网红直播影响力的品牌商动态定价决策研究

Research on Dynamic Pricing Decision of Brands Considering the Influence of Live Streaming

摘要: 随着直播电商的发展，网红主播的影响力在直播电商中发挥着不可忽视的力量，吸引了大量品牌商的关注。品牌商是否开通直播渠道以及如何发挥网红主播的影响力是其实现利益增长的重要问题。本文考虑网红主播的直播影响力，针对直播单一渠道和直播与直销双渠道，考虑每种渠道的“加价”和“佣金”两种模式，分别探究品牌商和网红主播的最优定价策略，并分析网红主播的影响力、直播市场需求比例对品牌商和网红主播均衡决策的影响。研究结果表明：产品的直播价格和网红主播的服务努力程度都将随着时间的推移而达到稳定状态，且取决于网红主播的初始引流量以及稳态网红主播引流量之间的差距；网红主播的影响力较大时，品牌商更愿意降低产品直播价格，进一步激励网红主播的直播服务努力程度，从而实现利润最优。相比于单渠道，“直销 + 直播”双渠道下供应链整体的利润更优，且网红“佣金”模式优于网红“加价”模式，只要网红主播和品牌商之间的佣金比例和坑位费设置合理，双方便可实现“双赢”。

Abstract: With the development of live broadcast e-commerce, the influence of online celebrity anchors has played an important role in live broadcast e-commerce, attracting the attention of a large number of brands. Whether brands open live broadcast channels and how to give full play to the influence of popular webmasters are important issues for their benefit growth. This paper considers the influence of online celebrity anchors on live broadcast, considers the “price increase” and “commission” models of each channel for single live broadcast channel and dual channels of live broadcast and direct sales, explores the optimal pricing strategies of brands and online celebrity anchors respectively, and analyzes the influence of online celebrity anchors and the influence of the proportion of live broadcast market demand on the balanced decision-making of brands and online celebrity anchors. The research results show that both the live broadcast price of the product and the service effort of the popular webmaster will reach a stable state over time, and depend on the difference between the initial traffic volume of the popular webmaster and the traffic volume of the stable popular webmaster; When online celebrity anchors have great influence, brands are more willing to reduce the price of live product, further stimulate the efforts of online celebrity anchors in live service, so as to achieve the optimal profit. Compared with the single channel, the overall profit of the supply chain under the dual channel of “direct sales + live broadcast” is better, and the online celebrity “commission” mode is better than the online celebrity “price increase” mode. As long as the commission ratio and pit fee between the online celebrity anchor and the brand are set reasonably, both parties can achieve a “double-win”.

1. 引言

近年来，网红直播带货作为一种新的营销手段，受到了众多品牌商家和人们的追捧。根据数据显示，截至2020年5月份月网络直播用户规模达5.60亿，占网民整体的62.0%，直播销售总额超过9000亿元，占到网络销售总体规模近10%。由此可见，网红直播带货正在改变着电商市场的格局。

随着2016年淘宝直播的正式上线，电商开启了直播浪潮。进入2018年后，网红直播带货迎来了首次快速增长，直播作为一种新型销售渠道闯入传统电商行业，且逐渐由一种社会现象演变成经济发展常态，特别是2020年抗击新冠疫情期间，直播带货更是成为了刺激国内消费，促进我国经济增长的新助力，政府部门相继出台支持政策，不断推进“互联网+”，打造数字化经济新优势，直播带货作为电商新晋“宠儿”，受到了各个行业的青睐。到如今，直播带货已经逐渐常态化，成为了供应链企业提高利润的新型策略。

直播带货过程中，网红主播是整个直播的核心所在，其自身的粉丝基础及影响力就是最好的宣传，利用好网红优势，把握好网红身后千千万万的“粉丝”群体，通过直播平台将一些博人眼球或是专业化的内容转化为购买力，将流量、知名度等一系列热度变现。相较于传统的线上直销渠道，网红直播拥有着更为生动的传播效果，利用一种活动式的销售方法更容易吸引消费者的眼球，加之网红本身所具有的粉丝信誉度，更是起到了博人眼球的效果。然而，网红直播带货渠道的热潮下，是对传统直销电商的巨大冲击。目前，在考虑网红主播的影响力以及合作模式的不同下，如何更好地利用网红直播实现利润最大化是品牌商家所面临的重大难题。

因此，本文在传统直销渠道下引入网红主播直播渠道，由单一的直销模式扩展为双渠道销售模式；同时，基于品牌商和网红主播间的不同合作模式，考虑网红直播影响力对产品需求的动态影响，通过构建其动态微分方程，分析不同策略下品牌商和网红的最优决策，探讨品牌商家是否引入网红直播渠道，以及直播渠道下如何更好的与网红主播合作，分析网红主播的影响力、直播市场需求比例等参数对供应链企业决策的影响。

2. 国内外研究现状

与本文相关的研究主要集中在直播电商供应链和动态定价两个方面。

目前，关于直播电商供应链问题的研究相对较少，多集中为实证研究，从直播的发展模式、作用机理以及盈利模式等方面展开研究。刘凤军 [1] 等基于拟社会交往和心流理论，探讨网红直播对消费者购买意愿的影响。梁玲 [2] 等以ABC态度理论为基础，探究直播带货下用户购买行为的影响因素状况及机理结果。少数学者将直播纳入供应链运营管理，运用数学建模的思想和方法，通过构建相关供应链成员博弈模型，研究直播电商供应链中运营决策相关问题。Wang [3] 等从薪酬机制的角度，考虑了工会、平台与主播之间的互动关系，分析了工会最优薪酬机制的性质，并进一步分析平台对工会和主播的分成率对联盟薪酬机制的影响。郑森圭 [4] 等人针对直播平台盈利不足问题，以委托代理为基础，分别考虑主播不签约和主播签约两种情形下对直播平台打赏收入分成模式进行研究。邢鹏 [5] 等人考虑了直播服务平台的营销努力与主播的服务质量交互作用的影响，并将其纳入决策模型，运用博弈论的方法分析直播电商供应链的服务质量努力问题。郭延禄 [6] 等人重点关注了直播带货下的产品质量问题，运用三方博弈演化模型探究网红直播带货中产品质量问题出现的机理，深入探讨了网红主播风险态度变化对直播带货努力的影响。于天阳 [7] 等考虑需求受网红直播带货影响，分别构建网红主导、电商卖家主导和双方权利对等三种不同权力结构下的供应链决策模型，探究权力结构和直播营销成本效率等对供应链成员最优决策的影响。

国内外学者关于供应链中动态定价的相关研究成果较多，大多学者运用动态微分博弈，针对广告投入、减排技术投入以及库存等方面展开动态策略研究。鲁馨蔓 [8] 等人考虑了产品技术先进度的时间因素，运用微分动态博弈的方法，分别探讨了创新成本分担和收益共享两种契约下云服务产品最优动态定价及技术创新决策。段永瑞 [9] 等人从不考虑参照效应和考虑参照效应两种情形下分别探讨自有品牌的最优动态定价策略。徐琪 [10] 等人采用动态规划的方法，研究双边平台匹配努力下的共享供应链动态定价问题。叶欣 [11] 等人运用微分方程刻画产品的商誉和减排量的动态变化，分析了单一渠道和双渠道下供应链成员的最优均衡决策，并运用广告合作–减排成本分担契约对供应链进行协调。胡娇 [12] 等人在考虑参照效应和主播影响力情形下研究直播平台和主播的合作决策问题，并进一步分析了参照效应和主播影响力对供应链个成员均衡决策的影响。

上述文献可以发现，网红直播确实会对用户的购买行为产生影响，目前而言，只有少数的学者将网红直播考虑到供应链运营策略研究中，对直播平台以及主播之间的合作和收入分成问题展开了探讨。但是，尚未有学者考虑网红主播的影响力对产品需求的影响，基于此，本文考虑网红主播的影响力对需求的影响，将网红主播的引流量作为状态变量构建微分博弈模型，探究不同渠道模式下品牌商和网红主播的合作策略，并分析网红主播的影响力对最优均衡决策的影响。

3. 问题描述及假设

考虑由一个品牌商和一个网红主播构成的二级供应链。品牌商拥有线上直销和线上直播两种销售渠道，既可以选择单一线上直销或单一线上直播的单一渠道销售，也可以选择线上直销和线上直播双渠道销售产品。线上直播渠道需要与网红主播合作，通过网红主播线上直播与粉丝互动来销售产品。网红主播对“粉丝”群体采取定向营销，以一些博人眼球或专业化内容等将粉丝转化为真实的消费者，实现流量的转移。网红主播的庞大粉丝群体及其强大影响力是线上直播相较于线上直销的最大优势。品牌商与网红主播间的合作模式主要有两种(如图1和图2所示)：一种是网红“加价”模式，即由品牌商为网红提供产品的批发价格 $w\left(t\right)$，网红在批发价的基础上加价 $d\left(t\right)$，以 $w\left(t\right)+d\left(t\right)$ 的价格销售给消费者，网红主播赚取加价利润；另一种是“佣金”模式，即品牌商决策产品的销售价格 $p_e\left(t\right)$，同时支付网红一定比例 $\lambda$ 的佣金和坑位费F，网红主播决策直播的服务 $s\left(t\right)$，两种模式下，网红主播的影响力对销售量均起着至关重要的作用。现实中，网红直播带货时的短时间内网红的影响力所带来的销售红利并不会递减，但是对于长期直播而言，也即多次直播后，网红主播的直播影响力对粉丝的影响将递减，市场的潜在需求量也会随时间的推移而发生变化。因此，本文考虑网红主播的影响力，动态地刻画网红主播引流量的变化，探讨不同合作模式下品牌商和网红主播的最优定价和服务决策问题。

本文研究基于如下假设：

假设1：网红直播带货下，网红主播的自身影响力对市场潜在需求具有拓展作用，且当网红主播的直播服务努力水平越高，其对潜在市场的拓展量越大。网红主播的直播服务努力水平是指网红为了保证直播带货效果所做的努力，例如网红在带货语言技术、专业能力、粉丝互动等过程中付出的努力。在直播中，通常网红的影响力越大，选择进入网红直播间的观众会越多；网红直播间的服务努力水平越高，直播间选择停留观看的观众越多，从竞争直播间中争夺的观众也越多，从而市场的潜在需求拓展量也越大。考虑到市场潜在需求拓展量的变化与商誉的变化情况相似，这里借鉴市场广告商誉模型，描述网红引流量的微分方程如下：

$\text{d}N\left(t\right)=\left[\phi s\left(t\right)-\mu N\left(t\right)\right]\text{d}t$ (1)

$N\left(0\right)=\phi N_0\ge 0$ (2)

其中， $\phi$ 表示网红直播影响力， $\phi$ 越大表明网红单位直播服务努力程度对网红引流量的影响越大。 $\mu$ 表示网红引流量的衰减系数。由于消费者会在竞争网红直播间转移，因而网红直播服务努力和平台的直播质量等都会造成网红引流量的衰减。

假设2：产品的需求受到产品价格和渠道竞争价格的影响，网红直播带货和自营直销下的需求函数如下：

$Q_e=\alpha +N\left(t\right)-p_e\left(t\right)+m\left(p_d\left(t\right)-p_e\left(t\right)\right)$ (3)

$Q_d=1-\alpha -p_d\left(t\right)+m\left(p_e\left(t\right)-p_d\left(t\right)\right)$ (4)

假设3：网红直播服务成本随着直播服务努力水平的提高而增大，假设其成本函数为 $G=\frac{c{s}^2}{2}$，其中，c为直播服务成本系数，系数越大，网红服务成本也越大。

假设4：品牌商家和网红的贴现率均为 $\rho$，决策期为 $[0,\infty )$。

本文主要的参数设定及符号说明如下表1：

Table 1. Description of parameters and symbols

表1. 参数及符号说明

4. 模型的构建及求解

本节从单渠道和双渠道两个角度出发，考虑网红主播影响力，探讨品牌商和网红主播间“加价”和“佣金”两种模式下，品牌商的最优动态定价策略以及网红主播的最优直播服务努力程度。

4.1. 单一渠道模式

对于单一渠道，我们分单一线上直销基础模式、单一直播加价模式和单一直播佣金模式三种讨论。

4.1.1. 单一线上直销基础模式(策略NT)

首先构建品牌商不选择与网红主播间合作时的单一直销渠道基础模型。当品牌商只开通线上直销模式，并且品牌商和网红主播间没有合作，产品的需求不受渠道竞争的影响，同时也不受主播影响力的影响，即 $Q_d^{NT}=1-p_d\left(t\right)$，品牌商的目标利润函数为：

$\underset{p_d\left(t\right)}{\max }{\pi }_M^{NT}=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\left\{p_d\left(t\right)\left[1-p_d\left(t\right)\right]\right\}\text{d}t}$ (5)

可以求得最优的产品直销价格为： $p_d^{NT}=\frac{1}{2}$，品牌商的最优利润为 ${\pi }_M^{NT}=\frac{\rho }{4}$。

4.1.2. 单一直播加价模式(策略NY)

品牌商和网红主播合作下，单一渠道分为“加价”模式和“佣金”模式两类。

单一渠道“加价”模式下，品牌商只开通单一线上直播渠道，品牌商和网红主播之间存在合作，产品的需求不受渠道竞争的影响，但受主播影响力的影响，也即需求受网红直播引流量的影响，此时需求为 $Q_e^{NY}=\alpha +N\left(t\right)-p_e\left(t\right)$。

品牌商为网红提供产品的最低价格w，由网红主播自主决策加价d，同时决策直播服务水平s，通过直播将产品销售给消费者，网红赚取差价获利。品牌商和网红主播的目标利润函数为：

$\underset{w\left(t\right)}{\max }{\pi }_M^{NY}=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\left\{w\left(t\right)\left[\alpha -\left(w\left(t\right)+d\left(t\right)\right)+N\left(t\right)\right]\right\}\text{d}t}$ (6)

$\underset{d\left(t\right),s\left(t\right)}{\max }{\pi }_O^{NY}=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\left\{d\left(t\right)\left[\alpha -\left(w\left(t\right)+d\left(t\right)\right)+N\left(t\right)\right]-\frac{c{s}^2\left(t\right)}{2}\right\}\text{d}t}$ (7)

根据stackelberg博弈时序，可以将该供应链系统的微分博弈模型概括如下。

$\begin{array}{l}\underset{w}{\max }{\pi }_M^{NY}\left(w;s,d\right)\\ \text{s}\text{.t}\{\begin{array}{l}\underset{s,d}{\max }{\pi }_O^{NY}\left(w;s,d\right)\\ \text{d}N\left(t\right)=\left[\phi s\left(t\right)-\mu N\left(t\right)\right]\text{d}t,N\left(0\right)=\phi N_0\ge 0\end{array}\end{array}$ (8)

为了确保系统收敛到有效的稳态，设定以下约束： $4\mu \left(\rho -3\mu \right)<\frac{{\phi }^2}{2c}<{\left(2\mu -\rho \right)}^2$

由上述式(7)~式(9)及约束，我们可以得到命题1。

命题1当品牌商只开通线上直播模式，且与网红主播采取加价模式时，品牌商的最优批发价格为 $w^{NY*}=\frac{\alpha +N}{2}$，网红主播的最优加价和直播服务水平决策为 $d^{NY*}=\frac{N+\alpha }{4},s^{NY*}=\frac{\phi V_O^{-Y}}{c}$，产品的直播价格为： $p_e^{NY*}=w+d=\frac{3\left(N+\alpha \right)}{4}$。

从命题1可知采用单一直播加价模式时为了获得品牌商与网红主播均衡stackelberg策略，必须确定网红主播的最优值函数的具体形式。

命题2 品牌商家和网红主播的最优值函数为：

$\{\begin{array}{l}{V}^{M*}=a_1^{NY*}{N}^2+a_2^{NY*}N+a_3^{NY*}\\ V^{O*}=b_1^{NY*}{N}^2+b_2^{NY*}N+b_3^{NY*}\end{array}$ (9)

其中：

$\{\begin{array}{l}{a}_1^{NY*}=\frac{1}{8f}\\ a_2^{NY*}=\frac{\alpha \left(4cf\left(f+\rho \right)+{\phi }^2\right)}{8cf{\left(f+\rho \right)}^2}\\ a_3^{NY*}=\frac{{\alpha }^2\left(4c^{2}f{\left(f+\rho \right)}^3+4cf{\phi }^2\left(f+\rho \right)+{\phi }^4\right)}{32c^{2}f\rho {\left(f+\rho \right)}^3}\end{array}$， $\{\begin{array}{l}{b}_1^{NY*}=\frac{c\left(-f-2\mu +\rho \right)}{4{\phi }^2}\\ b_2^{NY*}=\frac{\alpha }{4\left(f+\rho \right)}\\ b_3^{NY*}=\frac{{\alpha }^2\left(2c{\left(f+\rho \right)}^2+{\phi }^2\right)}{32c\rho {\left(f+\rho \right)}^2}\end{array}$

命题3 当品牌商与网红主播选择单一直播“加价”模式时，该直播电商供应链系统的动态均衡stackelberg策略为：

$w^{NY*}=w^{NY**}+\frac{1}{2}\left(\phi N_0-N^{**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -4\mu -f\right)}$ (10)

$d^{NY*}=d^{NY**}+\frac{1}{4}\left(\phi N_0-N^{NY**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -4\mu -f\right)}$ (11)

$s^{NY*}=s^{NY**}+\left(\frac{\rho -2\mu -f}{2\phi }\right)\left(\phi N_0-N^{NY**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -4\mu -f\right)}$ (12)

$p_e^{NY*}=p_e^{NY**}+\frac{3}{4}\left(\phi N_0-N^{NY**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -4\mu -f\right)}$ (13)

$N^{NY*}=\left(\phi N_0-N^{NY**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -4\mu -f\right)}+N^{NY**}$ (14)

其中： $w^{NY**}=\frac{\alpha }{2}$ ； $d^{NY**}=\frac{\alpha }{4}$ ； $p_e^{NY**}=\frac{3\alpha }{4}$ ； $s^{NY**}=\frac{6\alpha \mu \phi -2\alpha \rho \phi +2\alpha \phi f}{16c{\mu }^2-2{\phi }^2+16c\mu f}$

$N^{NY**}=\frac{\alpha {\phi }^2}{-8c{\mu }^2+{\phi }^2-8c\mu f}$ ； $f=\sqrt{{\left(2\mu -\rho \right)}^2-\frac{{\phi }^2}{2c}}$

由命题1和命题3可以推出，单一直播加价模式下，稳态均衡策略下网红主播会在品牌商给定的批发价基础上进行加价50%，即 $d^{NY**}=\frac{1}{2}{w}^{NY**}$，当直播的销售市场规模 $\alpha <\frac{2}{3}$ 时，产品的直播价格相对于单一直销模式的产品价格较低。

由以上讨论，可以看到，在单一直播加价模式下，网红主播的直播服务努力程度随时间的而单调变化，且取决于网红主播的初始引流量以及稳态网红主播引流量之间的差距。当网红主播的影响力较大，初始引流量大于稳态引流量，网红主播的直播服务努力程度最初较高，随着时间推移将不断降低；当网红主播的影响力较小，初始引流量小于稳态引流量，则网红主播的直播服务努力程度随着时间的推移不断提高；当网红直播的初始引流量和稳态引流量一致，则其直播服务努力程度将保持在稳定状态。对于网红主播而言，当其本身的影响力较大时，直播的服务努力收获的边际效益较低，网红主播在直播服务努力程度方面缺乏动力。而对于影响力较小的网红主播而言，为了更好的销售产品，必须加强直播服务努力程度，吸引直播间的观众留存。

此外，品牌商和网红主播的均衡动态定价策略受到网红初始引流量和稳态引流量的影响。

当网红主播的初始引流量大于稳态均衡引流量时 $\left(\phi N_0>N^{NY**}\right)$，品牌商和网红主播采取价格撇除策略，即随着时间的推移，降低产品的批发价和网红加价。当网红主播的初始引流量小于稳态均衡引流量 $\left(\phi N_0<N^{NY**}\right)$，品牌商和网红主播采取价格渗透策略，即随着时间的推移，其产品的批发价和网红加价均随之提高。当网红主播的初始引流量等于稳态均衡引流量 $\left(\phi N_0=N^{NY**}\right)$，品牌商和网红主播均采取价格不变策略，产品的批发价及网红加价均保持恒定状态。这一推论很好的证实了现实中例子。对于初始影响力较大的网红主播，由于单位服务努力程度引流量边际效益小，将随着时间推移不断降低直播服务努力程度，从而会造成直播间消费者的流失，此后为了更好的吸引顾客实现利润最大，只能降低产品的直播价格。

4.1.3. 单一直播佣金模式(策略NR)

当品牌商和网红主播采取单一直播佣金模式时，品牌商家首先决策直播价格 $p_e$，网红主播决策直播服务努力水平s。品牌商通过直播渠道，借助网红直播影响力将产品销售给消费者，制造商需支付网红一定比例 $\lambda$ 的佣金和固定坑位费F。此模式下，品牌商和网红主播的目标利润函数分别为：

$\underset{p_e\left(t\right)}{\max }{\pi }_M^{NR}=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\left\{\left(1-\lambda \right)p_e\left(t\right)\left[\alpha -p_e\left(t\right)+N\left(t\right)\right]-F\right\}\text{d}t}$ (15)

$\underset{s\left(t\right)}{\max }{\pi }_O^{NR}=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\left\{\lambda p_e\left(t\right)\left[\alpha -p_e\left(t\right)+N\left(t\right)\right]-\frac{c{s}^2\left(t\right)}{2}+F\right\}\text{d}t}$ (16)

根据stackelberg博弈时序，该佣金模式下的电商直播供应链系统的微分博弈模型如下：

$\begin{array}{l}\underset{p_e}{\max }{\pi }_M^{NR}\left(p_e;s\right)\\ \text{s}\text{.t}\{\begin{array}{l}\underset{s}{\max }{\pi }_O^{NR}\left(p_e;s\right)\\ \text{d}N\left(t\right)=\left[\phi s\left(t\right)-\mu N\left(t\right)\right]\text{d}t,N\left(0\right)=\phi N_0\ge 0\end{array}\end{array}$ (17)

为了确保系统收敛到有效的稳态，需要设定以下约束： $2{\mu }^2+2\mu \rho \in \left[\frac{\lambda {\phi }^2}{c}-{\rho }^2,\frac{\lambda {\phi }^2}{c}\right]$

命题4 当品牌商只开通线上直播模式，且与网红主播采取佣金模式时，品牌商的最优直播价格为 $p_e^{NR*}=\frac{\alpha +N}{2}$，网红主播的最优决策为 $s^{NR*}=\frac{\phi V_O^{NR*}\text{'}\left(N\right)}{c}$。

由命题4可知，当 $\alpha +N>1$ 时，单一直播渠道且采取佣金模式时，产品的直播价格将会高于单一直销渠道下产品直销价格。这也说明，在一定的网红主播影响力下，在单一的直播渠道下，采取佣金模式时，产品的直播价格更高，但是网红加价模式下的产品直播价格对 $\alpha$ 的敏感度较高。

命题5 品牌商家和网红主播的最优值函数为：

$\{\begin{array}{l}{V}_M^{NR*}=a_4^{NR*}{N}^2+a_5^{NR*}N+a_6^{NR*}\\ V_O^{NR*}=b_4^{NR*}{N}^2+b_5^{NR*}N+b_6^{NR*}\end{array}$ (18)

其中：

$\{\begin{array}{l}{a}_4^{NR*}=-\frac{\lambda -1}{4\left(M+{\rho }^2-\rho \right)}\\ a_5^{NR*}=-\frac{\alpha \left(\lambda -1\right)\left(c\left({\rho }^{2}M+4{\mu }^2+4\mu \rho +{\rho }^3\right)-\lambda {\phi }^2\right)}{c\left(M+\rho \right)\left(M+{\rho }^2-\rho \right)\left(M+2{\rho }^2-\rho \right)}\\ a_6^{NR*}=\frac{{\alpha }^2\left(-\lambda \right)+{\alpha }^2-4F}{4{\rho }^2}-\frac{{\alpha }^2\left(\lambda -1\right)\lambda {\phi }^2\left(c\left({\rho }^{2}M+4{\mu }^2+4\mu \rho +{\rho }^3\right)-\lambda {\phi }^2\right)}{{\rho }^2{c}^2{\left(M+\rho \right)}^2\left(M+{\rho }^2-\rho \right)\left(M+2{\rho }^2-\rho \right)}\end{array}$ (19)

$\{\begin{array}{l}{b}_4^{NR*}=\frac{c\left(-M+2\mu +\rho \right)}{4{\phi }^2}\\ b_5^{NR*}=\frac{\alpha \lambda }{M+\rho }\\ b_6^{NR*}=\frac{{\alpha }^2{\lambda }^2{\phi }^2}{2c\rho {\left(M+\rho \right)}^2}+\frac{{\alpha }^2\lambda +4F}{4\rho }\end{array}$ (20)

其中： $M=\sqrt{\frac{c{\left(2\mu +\rho \right)}^2-2\lambda {\phi }^2}{c}}$。

由此，根据命题4可得，网红主播的最优决策为 $s^{NR*}=\frac{2\alpha \lambda {\phi }^2-cN\left(M^2-2M\mu -\rho \left(2\mu +\rho \right)\right)}{2c\phi \left(M+\rho \right)}$。

命题6 当品牌商与网红主播选择单一直播“佣金”模式时，该电商直播供应链系统的动态均衡stackelberg策略为：

$p_e^{NR*}=p_e^{NR**}+\frac{1}{2}\left(\phi N_0-N^{NR**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -M\right)}$ (21)

$s^{NR*}=s^{NR**}+\left(\frac{2\mu +\rho -M}{2\phi }\right)\left(\phi N_0-N^{NR**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -M\right)}$ (22)

$N^{NR*}=\left(\phi N_0-N^{NR**}\right){\text{e}}^{-\frac{1}{2}t\left(\rho -M\right)}+N^{**}$ (23)

其中： $p_e^{NR**}=\frac{\alpha \left(c\mu \left(\mu +\rho \right)-\lambda {\phi }^2\right)}{2c\mu \left(\mu +\rho \right)-\lambda {\phi }^2}$， $s^{NR**}=\frac{\alpha \lambda \phi \left(-M+\mu +\rho \right)}{\lambda {\phi }^2-2c\mu \left(\mu +\rho \right)}$， $N^{NR**}=-\frac{\alpha \lambda {\phi }^2}{2c\mu \left(\mu +\rho \right)-\lambda {\phi }^2}$。

由命题6可知，单一直播佣金模式下，产品的直播价格 $p_e^{NR**}<\frac{\alpha }{2}$，与单一渠道策略对比，其产品的

稳态均衡价格最低。单一直播佣金模式下，稳态均很产品的直播价格、网红主播服务努力程度以及网红引流量随时间单调变化，且受网红初始引流量和稳态均衡引流量间差距影响，其影响与单一直播加价模式下情况类似。

4.2. 双渠道销售模式

双渠道是指品牌商不仅开通线上直销渠道，且开通线上直播渠道，借助网红主播的影响力来扩大产品的需求。

4.2.1. 网红“加价”模式下(策略Y)

当品牌商选择“加价”模式时，品牌商为网红提供产品的最低价格w，同时决策直销渠道产品价格 $p_d$，由网红主播自主决策加价d，并决策直播服务水平s，通过直播将产品销售给消费者，网红通过赚取差价获利。此时，直销和直播双渠道下品牌商的目标利润函数为：

$\begin{array}{c}\underset{w\left(t\right),p_d\left(t\right)}{\max }{\pi }_M^Y=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\{w\left(t\right)\left[\alpha -\left(w\left(t\right)+d\left(t\right)\right)+m\left(p_d\left(t\right)-w\left(t\right)-d\left(t\right)\right)+N\left(t\right)\right]}\\ +p_d\left(t\right)\left[1-\alpha -p_d\left(t\right)+m\left(w\left(t\right)+d\left(t\right)-p_d\left(t\right)\right)\right]\}\text{d}t\end{array}$ (24)

网红主播的目标利润函数为：

$\underset{d\left(t\right),s\left(t\right)}{\max }{\pi }_O^Y=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-\rho t}\left\{d\left(t\right)\left[\alpha -\left(w\left(t\right)+d\left(t\right)\right)+m\left(p_d\left(t\right)-w\left(t\right)-d\left(t\right)\right)+N\left(t\right)\right]-\frac{c{s}^2\left(t\right)}{2}\right\}\text{d}t}$ (25)

根据stackelberg博弈时序，该双渠道电商直播供应链系统的微分博弈模型如下：

$\begin{array}{l}\underset{w,p_d}{\max }{\pi }_M^Y\left(w,p_d;s,d\right)\\ \text{s}\text{.t}\{\begin{array}{l}\underset{s,d}{\max }{\pi }_O^Y\left(w,p_d;s,d\right)\\ \text{d}N\left(t\right)=\left[\phi s\left(t\right)-\mu N\left(t\right)\right]\text{d}t,N\left(0\right)=\phi N_0\ge 0\end{array}\end{array}$ (26)

为了获取网红“加价”模式合同下供应链系统的动态均衡策略，首先利用逆向归纳法获取网红主播的服务努力水平和加价价格的反应策略，然后基于网红主播的反应策略获取品牌商家的直销价格和批发价格的最优策略。

命题7 直销与直播双渠道下品牌商选择网红“加价”合同时，网红主播的服务努力水平和加价价格的反应策略为：

$s^{Y*}=\frac{V_O^{Y*}\text{'}\left(N\right)\phi }{c}=\frac{\left(2b_1^{Y*}N+b_2^{Y*}\right)\phi }{c}$ (27)

$d^{Y*}=\frac{N-w-mw+\alpha +m{p}_d}{2\left(1+m\right)}$ (28)

证明：给定品牌商家的直播价格 $p_e$ 和批发价格w，利用最优控制理论，可得网红主播的服务努力水平和加价价格策略应该满足HJP (哈密尔顿–雅克比–贝尔曼)方程。

$H_O^Y=\rho V_O^{Y*}=\underset{s,d}{\max }\left\{d\left(\alpha -\left(w+d\right)+m\left(p_d-w-d\right)+N\right)-\frac{c{s}^2}{2}+V_O^{Y*}\text{'}\left(N\right)\left(\phi s-\mu N\right)\right\}$ (29)

其中， $V^{RO}$ 为Y策略下网红主播的最优值函数， $V_N^{YO}$ 为网红主播的最优值函数对网红引流量N的一阶偏导数，求解式(25)右端的最优化，得到网红主播的直播服务努力水平和加价价格的反应策略：

$s^{Y*}=\frac{\phi V_O^{Y*}\text{'}\left(N\right)}{c}$， $d^{Y*}=\frac{N-w-mw+\alpha +m{p}_d}{2\left(1+m\right)}$。

由此可看到，双渠道网红“加价”模式下，品牌商的批发价格较低时，网红加价高；且网红的加价价格会随着直销渠道与直播渠道间的竞争而减小。

该结论由式(29)可知， $\frac{\partial d^{Y*}}{\partial w}=\frac{-1}{2}<0$， $\frac{\partial d^{Y*}}{\partial m}=-\frac{N+\alpha -p_r}{2{\left(1+m\right)}^2}<0$，因此，网红主播的加价价格与批发

价格和渠道竞争系数成反比。也就是说，当网红的直播产品批发价格较低时，网红的加价价格将会越高，其利润空间也会越大；而当产品的批发价格越高时，网红将通过降低加价价格来扩大产品的需求，从而实现利润最优。同时，直播和直销渠道间的竞争越大，直播价格与直销价格差异对需求的影响也越大，网红会更愿意降低加价扩大产品的需求。

命题8 直销与直播双渠道下品牌商选择网红“加价”合同时，品牌商的最优批发价格和最优直销价格为：

$p_d^{Y*}=\frac{m-\alpha +Nm+1}{4m+2}$ (30)

$w^{Y*}=\frac{N+\alpha +m+Nm}{4m+2}$ (31)

网红主播的最优加价价格为：

$d^{Y*}=\frac{N+\alpha }{4+4m}$ (32)

产品的直播价格为：

$w^{Y*}+d^{Y*}=\frac{N+m+Nm+\alpha }{2+4m}+\frac{N+\alpha }{4+4m}$ (33)

通过对命题8分析可知，在网红“加价”模式下，品牌方的动态最优批发价、最优直销价格和网红的最优加价价格均随着网红引流量的变化而变化。由式(31)~式(32)可得 $\frac{\partial w^{Y*}}{\partial N}=\frac{1+m}{4m+2}>0$， $\frac{\partial p_d^{Y*}}{\partial N}=\frac{m}{4m+2}>0$， $\frac{\partial d^{Y*}}{\partial N}=\frac{1}{4m+4}>0$，显而易见，品牌方的动态最优批发价、最优直销价格和网红的最优加价价格均随着网

红引流量的提高而增加，且产品的直播价格比直销价格对网红引流量的反应更敏感。另外，最优的批发价格和加价价格会随着直播渠道需求比例的扩大而提高，而最优的直销价格会随着直播需求比例的扩大而降低。也就是说，当消费者更愿意在直播间购买产品时，直播间的价格可以适当提高；而直销渠道的价格应该降低，用低价吸引消费者进行购买。

证明：为了获得品牌商的最优批发价格和最优直播价格，将式(28)和式(29)代入品牌商的目标利润函数式(25)。利用最优控制理论，品牌商的最优策略应该满足HJP (哈密尔顿–雅克比–贝尔曼)方程，即：

$\begin{array}{l}{H}_M^Y=\rho V_M^{Y*}=\underset{p_d,w}{\max }\{w\left[\alpha -\left(w+d\right)+m\left(p_d-w-d\right)+N\right]\\ +p_d\left[1-\alpha -p_d+m\left(w+d-p_d\right)\right]+V_M^{Y*}\text{'}\left(N\right)\left(\phi s-\mu N\right)\}\end{array}$ (34)

其中， $V^{YM}$ 为Y策略下品牌商的最优值函数， $V_N^{YM}$ 为品牌商的最优值函数对网红引流量N的一阶偏导数，将式子(29)代入式(35)，然后求解式(35)右端的最优化，得到品牌商的最优直销价格和最优直播价格策略：

$p_d^{Y*}=\frac{m-\alpha +Nm+1}{4m+2}$， $w^{Y*}=\frac{N+\alpha +m+Nm}{4m+2}$

从命题7、8可知为了获得品牌商家采用网红“加价”模式时，供应链的均衡stackelberg策略，必须确定品牌商家和网红主播的最优值函数的具体形式。这将面临偏微分方程求解问题。为此，下面给出了最优值函数的具体求解过程。

命题9 品牌商家和网红主播的最优值函数为：

$\{\begin{array}{l}{V}_M^{Y*}=a_1^{Y*}{N}^2+a_2^{Y*}N+a_3^{Y*}\\ V_O^{Y*}=b_1^{Y*}{N}^2+b_2^{Y*}N+b_3^{Y*}\end{array}$ (35)

其中：

$\{\begin{array}{l}{a}_1^{Y*}=-\frac{c\left(1+2m+2m^2\right)}{8\left(1+m\right)\left(1+2m\right)\left(2c\mu -c\rho +4{\phi }^2{b}_1\right)}\\ a_2^{Y*}=-\frac{c\left(2m+2m^2+\alpha \right)+8\left(1+3m+2m^2\right){\phi }^2{a}_1{b}_2}{4\left(1+m\right)\left(1+2m\right)\left(c\left(\mu -\rho \right)+2{\phi }^2{b}_1\right)}\\ a_3^{Y*}=\frac{c\left(2+2m^2-4\alpha +3{\alpha }^2+2m\left(2-2\alpha +{\alpha }^2\right)\right)+8\left(1+3m+2m^2\right){\phi }^2{a}_2{b}_2}{8c\left(1+m\right)\left(1+2m\right)\rho }\end{array}$ (36)

$\{\begin{array}{l}{b}_1^{Y*}=\frac{-c\left(2\mu -\rho +\sqrt{{\left(\rho -2\mu \right)}^2-\frac{{\phi }^2}{2c\left(1+m\right)}}\right)}{4{\phi }^2}\\ b_2^{Y*}=-\frac{c\alpha }{8\left(1+m\right)\left(c\mu -c\rho +2{\phi }^2{b}_1\right)}\\ b_3^{Y*}=\frac{b_2^2{\phi }^2}{2c\rho }+\frac{{\alpha }^2}{16\rho \left(1+m\right)}\end{array}$ (37)

证明：为了确定品牌商家和网红主播的最优值函数 $V^{M*}$ 和 $V^{O*}$。我们将命题8中的动态均衡策略代入式(31)~式(33)，得到品牌商家和网红主播最优值函数满足的偏微分方程组。

$\begin{array}{l}\rho \left(a_1{N}^2+a_{2}N+a_3\right)\\ \equiv \frac{N^2\left(c\left(1+2m+2m^2\right)+16c\left(1+3m+2m^2\right)\mu a_1+32\left(1+3m+2m^2\right){\phi }^2{a}_1{b}_1\right)}{8c\left(1+m\right)\left(1+2m\right)}\\ +\frac{N\left(2c\left(2m+2m^2+\alpha \right)+8c\left(1+3m+2m^2\right)\mu a_2+16\left(1+3m+2m^2\right){\phi }^2{a}_2{b}_1+16\left(1+3m+2m^2\right){\phi }^2{a}_1{b}_2\right)}{8c\left(1+m\right)\left(1+2m\right)}\\ +\frac{2c+2c{m}^2-4c\alpha +3c{\alpha }^2+2cm\left(2-2\alpha +{\alpha }^2\right)+8\left(1+3m+2m^2\right){\phi }^2{a}_2{b}_2}{8c\left(1+m\right)\left(1+2m\right)}\\ \rho \left(b_1{N}^2+b_{2}N+b_3\right)\equiv \frac{{\alpha }^2}{16\left(1+m\right)}+N^2\left(\frac{1}{16\left(1+m\right)}+2\mu b_1+\frac{2{\phi }^2{b}_1^2}{c}\right)+\frac{{\phi }^2{b}_2^2}{2c}+N\left(\frac{\alpha }{8\left(1+m\right)}+\mu b_2+\frac{2{\phi }^2{b}_1{b}_2}{c}\right)\end{array}$

为了求解以上方程，尝试一下待定系数的品牌商家和网红主播的最优值函数形式：

$\begin{array}{l}{V}_M^{Y*}=a_1{N}^2+a_{2}N+a_3\\ V_O^{Y*}=b_1{N}^2+b_{2}N+b_3\end{array}$

利用上式方程系数的恒等关系，可以得到待定系数可以满足的非线性方程组。接下来，利用上述非线性方程组获得待定系数。其过程是：首先计算 $b_1^{Y*}$，然后计算 $a_1^{Y*}$，随后计算 $a_2^{Y*}$ 和 $b_2^{Y*}$，最后确定 $a_3^{Y*}$ 和 $b_3^{Y*}$。

命题10 当品牌商与网红主播选择网红“加价”模式时，该双渠道供应链系统的动态均衡stackelberg策略为：

$w^{Y*}=w^{Y**}+\left(\frac{1+m}{4m+2}\right)\left(\phi N_0-N^{Y**}\right){\text{e}}^{-\left(\frac{2*b_4^{Y*}-c*\mu }{c}\right)t}$ (38)

$d^{Y*}=d^{Y**}+\left(\frac{1}{2m+2}\right)\left(\phi N_0-N_m^{Y**}\right){\text{e}}^{-\left(\frac{2*b_4^{Y*}-c*\mu }{c}\right)t}$ (39)

$p_d^{Y*}=p_d^{Y**}+\left(\frac{1+m}{4m+2}\right)\left(\phi N_0-N^{Y**}\right){\text{e}}^{-\left(\frac{2*b_4^{Y*}-c*\mu }{c}\right)t}$ (40)

$s^{Y*}=s^{Y**}+\left(\frac{2\mu +\rho -\rho A}{2\phi }\right)\left(\phi N_0-N^{Y**}\right){\text{e}}^{-\left(\frac{2*b_4^{Y*}-c*\mu }{c}\right)t}$ (41)

其中， $p_d^{Y**}=\frac{1+m-\alpha }{2+4m}-\frac{2m\alpha {\phi }^2}{c\left(1+m\right)\left(2+4m\right)\left(8\mu -2\rho +X\right)\left(2\rho +X\right)}$ ；

$w^{Y**}=\frac{m+\alpha }{2+4m}-\frac{2\alpha {\phi }^2}{c\left(2+4m\right)\left(8\mu -2\rho +X\right)\left(2\rho +X\right)}$ ；

$d^{Y**}=\frac{\alpha \left(-{\phi }^2+2c\left(1+m\right)\mu \left(2\mu +X\right)\right)}{c{\left(1+m\right)}^2\left(8\mu -2\rho +X\right)\left(2\rho +X\right)}$ ； $s^{Y**}=\frac{\alpha \phi \left(6\mu -2\rho +X\right)}{c\left(1+m\right)\left(8\mu -2\rho +X\right)\left(2\rho +X\right)}$

$X=\sqrt{4{\left(-2\mu +\rho \right)}^2-\frac{2{\phi }^2}{c+cm}}$

证明：根据命题7可以得到网红主播的服务水平反应函数： $s^{Y*}=\frac{\phi V_O^{Y*}\text{'}\left(N\right)}{c}=\frac{\phi \left(2b_1^{Y*}N+b_2^{Y*}\right)}{c}$，将其代入式(27)的约束条件，可以得到网红直播引流量的状态方程为： $\text{d}N\left(t\right)=\left[\frac{\left(2b_1^{Y*}{\phi }^2-c\mu \right)}{c}N+\frac{{\phi }^2{b}_2^{Y*}}{c}\right]\text{d}t$，随着时间的推移，网红直播的引流的稳态方程为：

$N_Y^{\text{*}*}=\left(\phi N_0-\frac{{\phi }^2{b}_2^{Y*}}{2b_1^{Y*}{\phi }^2-c\mu }\right){\text{e}}^{-\left(\frac{2b_1^{Y*}{\phi }^2-c\mu }{c}\right)t}+\frac{{\phi }^2{b}_2^{Y*}}{2b_1^{Y*}{\phi }^2-c\mu }$ (42)

为了保证引流量能在计划期内收敛，我们需要引入约束 $2b_1^{Y*}{\phi }^2-c\mu >0$，即 $\frac{{\phi }^2}{2c\left(1+m\right)}>4\mu \left(\rho -3\mu \right)$

将式(38)分别代入式(28) (29) (31) (32)，我们可以得到在网红“加价”模式下品牌商和网红主播的均衡决策式(39)至式(42)。

推论1：在双渠道网红“加价”模式下，直播渠道需求规模比例的变化会对网红直播引流量产生影响，进而会对品牌商和网红的产品决策产生影响，即：

$\frac{\partial N^{Y**}}{\partial \alpha }<0$， $\frac{\partial w^{Y**}}{\partial \alpha }>0$， $\frac{\partial d^{Y**}}{\partial \alpha }>0$， $\frac{\partial s^{Y**}}{\partial \alpha }>0$， $\frac{\partial p_d^{Y**}}{\partial \alpha }>0$ (43)

推论1表明，双渠道网红“加价”模式下，随着直播渠道需求规模比例的扩大，会使网红的直播服务水平降低，从而网红直播引流量将会降低，进而直播和直销两种渠道下的产品价格将会受到影响。首先，直播渠道下，随着直播需求比例的扩大，也就是说消费者更愿意从直播渠道购买产品，此时，品牌商应该通过提高产品的批发价来实现利润最大化，而网红也将提高产品的加价价格来获利，总体而言，产品的直播价格会随着直播需求比例的扩大而提高，呈现正向关系。其次，在品牌商的直销渠道下，直播需求规模比例对产品直销价格的影响比较复杂。

推论2：双渠道网红“加价”模式下，网红的直播影响力因子对直播和直销渠道价格决策产生反向影响，对网红的引流量产生正向影响，即

$\frac{\partial p_d^{Y**}}{\partial \phi }<0$， $\frac{\partial w^{Y**}}{\partial \phi }<0$， $\frac{\partial d^{Y**}}{\partial \phi }<0$， $\frac{\partial N^{Y**}}{\partial \phi }>0$ (44)

推论2表明，在网红“加价”模式下，网红直播影响力因子越大，即网红的影响力越大，网红直播的引流量将增大，产品两种渠道下的总需求量将会提高，直销与直播渠道产品的价格将越小。这与现实事实相符，网红的直播影响力越大，将会吸引更多的粉丝或受众下单，从而提高了直播渠道下产品的需求量；另外，直播渠道需求量越大，品牌商给出的批发价格会越低，网红也更喜欢通过低价来获取利润。对于直销渠道而言，品牌商也应该采取降低价格的策略来实现利润的最大化，这是因为降低直销价格可以减小两渠道间的价格竞争。

推论3：双渠道网红“加价”模式下，网红直播服务成本系数对直播和直销渠道价格决策产生正向影响，对网红的引流量产生反向影响，即

$\frac{\partial p_d^{Y**}}{\partial c}>0$， $\frac{\partial w^{Y**}}{\partial c}>0$， $\frac{\partial d^{Y**}}{\partial c}>0$， $\frac{\partial N^{Y**}}{\partial c}<0$ (45)

推论3表明，随着网红直播服务成本系数的变大，网红主播的直播服务成本越高，会使得网红的直播服务水平下降，从而导致网红直播的引流量越低。直播服务成本的提高会导致网红直播服务成本的增加，因此，为了实现利润最大化，网红应该提高加价价格。而对于品牌商而言，直播渠道下的产品存在边际效应，会更偏向于直销渠道下的销售，因此，品牌商应该提高产品批发价，促使更多的需求转移到直销渠道，同时直销渠道的价格也将会提高。

4.2.2. 佣金模式下(策略R)

直销与直播双渠道下，当品牌商选择佣金模式时，品牌商家首先决策直播价格 $p_e$ 和直销价格 $p_d$，通过直播渠道，借助网红直播影响力将产品销售给消费者，制造商需支付网红一定比例 $\lambda$ 的佣金和固定坑位费F，直播带货中，网红需决策直播服务努力水平s。此时，品牌商的目标利润函数为：

$\begin{array}{c}\underset{p_e\left(t\right),p_d\left(t\right)}{\max }{\pi }_M^R=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-rt}\{\left(1-\lambda \right)p_e\left(t\right)\left[\alpha -p_e\left(t\right)+m\left(p_d\left(t\right)-p_e\left(t\right)\right)+N\left(t\right)\right]}\\ +p_d\left(t\right)\left[1-\alpha -p_d\left(t\right)+m\left(p_e\left(t\right)-p_d\left(t\right)\right)\right]-F\}\text{d}t\end{array}$ (46)

网红的目标利润函数为：

$\underset{s\left(t\right)}{\max }{\pi }_O^R=E{\displaystyle \underset{0}{\overset{\infty }{\int }}{\text{e}}^{-rt}\left\{\lambda p_e\left(t\right)\left[\alpha -p_e\left(t\right)+m\left(p_d\left(t\right)-p_e\left(t\right)\right)+N\left(t\right)\right]-\frac{c{s}^2\left(t\right)}{2}+F\right\}\text{d}t}$ (47)

在该合同下，根据stackelberg博弈时序，可以将供应链系统的微分博弈模型概括如下。

$\begin{array}{l}\underset{p_e,p_d}{\max }{\pi }_M^R\left(p_e,p_d;s\right)\\ \text{s}\text{.t}\{\begin{array}{l}\underset{s}{\max }{\pi }_O^R\left(p_e,p_d;s\right)\\ \text{d}N\left(t\right)=\left[\phi s\left(t\right)-\mu N\left(t\right)\right]\text{d}t,N\left(0\right)=\phi N_0\ge 0\end{array}\end{array}$ (48)

为了获取佣金合同下供应链系统的动态均衡策略，首先利用逆向归纳法获取网红主播的服务努力水平的反应策略，然后基于网红主播的反应策略获取品牌商家的直播价格和直销价格的最优策略。

命题11 品牌商选择佣金合同时，网红主播的服务努力水平的反应策略为：

$s^{R*}=\frac{\phi V_O^{R*}\text{'}\left(N\right)}{c}$ (49)

证明同命题7。

命题12 双渠道下品牌商选择佣金合同时，品牌商的动态最优直销价格和最优直播价格为：

$p_d^{R*}=-\frac{\left(\lambda -1\right)\left(2\left(\alpha -1\right)+m\left(\alpha \lambda +N\left(\lambda -2\right)-2\right)\right)}{4\left(\lambda -1\right)+{\lambda }^2{m}^2+8\left(\lambda -1\right)m}$ (50)

$p_e^{R*}=\frac{2\left(\lambda -1\right)\left(\alpha +N\right)+m\left(\alpha \lambda +2N\left(\lambda -1\right)+\lambda -2\right)}{4\left(\lambda -1\right)+{\lambda }^2{m}^2+8\left(\lambda -1\right)m}$ (51)

为了保证产品的价格均有意义，故 $4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2<0$，即 $m^2{\lambda }^2<4\left(1+2m\right)\left(1-\lambda \right)$。

证明同命题8。

由命题12可知，产品的动态最优产品直销价格和直播价格均随着网红直播引流量的状态变化而变化，根据式(51) (52)得 $\frac{\partial p_e^{R*}}{\partial N}>0,\frac{\partial p_d^{R*}}{\partial N}>0$，故当网红主播的引流量提高时，品牌方应该适当的提高价格来获取利润的最大化，这表明消费者愿意为引流量大的网红直播产品买单。

命题13 品牌商家和网红主播的最优值函数为：

$\{\begin{array}{l}{V}_M^{R*}=a_4^{R*}{N}^2+a_5^{R*}N+a_6^{R*}\\ V_O^{R*}=b_4^{R*}{N}^2+b_5^{R*}N+b_6^{R*}\end{array}$ (52)

其中，

$\{\begin{array}{l}{a}_4^{R*}=-\frac{c\left(1+m\right){\left(-1+\lambda \right)}^2}{\left(-4-8m+4\lambda +8m\lambda +m^2{\lambda }^2\right)\left(2c\mu +c\rho -4{\phi }^2{b}_4\right)}\\ a_5^{R*}=\frac{-\frac{\left(-1+\lambda \right)\left(2\alpha \left(-1+\lambda \right)+m\left(-2+\lambda +\alpha \lambda \right)\right)}{\left(4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2\right)\rho }+\frac{2{\phi }^2{a}_4{b}_5}{c\rho }}{1+\frac{c\mu -2{\phi }^2{b}_4}{c\rho }}\\ a_6^{R*}=-\frac{F+\frac{\left(-1+\lambda \right)\left(-1+2\alpha +{\alpha }^2\left(-2+\lambda \right)+m\left(-1+\alpha \lambda \right)\right)}{4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2}-\frac{{\phi }^2{a}_5{b}_5}{c}}{\rho }\end{array}$

$\{\begin{array}{l}{b}_4^{R*}=\frac{c\left(2\mu +\rho \left(\rho -A\right)\right)}{4{\phi }^2}\\ b_5^{R*}=\frac{c\lambda L}{B^2\left(c\rho +\mu \rho +2b_4{\phi }^2\right)}\\ b_6^{R*}=\frac{F}{\rho }+\frac{b_5{}^2{\phi }^2}{2c\rho }+\frac{\lambda \left(\lambda m\left(1+m\right)+\alpha \left(-2+2\lambda -4m+3\lambda m\right)\right)\left(\left(-2+\lambda \right)m+\alpha \left(-2+\lambda \left(2+m\right)\right)\right)}{B^2\rho }\end{array}$

证明同命题9。

命题14 当品牌商与网红主播选择佣金模式时，供应链系统的稳态最优均衡stackelberg策略为：

$\begin{array}{l}{p}_e^{R*}=p_e^{R**}+\left(\frac{-2-2m+2\lambda +2m\lambda }{4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2}\right)\left(\phi N_0-N^{R**}\right){\text{e}}^{-\left(\frac{2\mu +{\rho }^2-\rho A}{2{\phi }^2}-\mu \right)t}\\ p_d^{R*}=p_d^{R**}+\left(-\frac{\left(-1+\lambda \right)\left(-2m+m\lambda \right)}{4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2}\right)\left(\phi N_0-N^{R**}\right){\text{e}}^{-\left(\frac{2\mu +{\rho }^2-\rho A}{2{\phi }^2}-\mu \right)t}\\ s^{R*}=s^{R**}+\left(\frac{2\mu +\rho -\rho A}{2\phi }\right)\left(\phi N_0-N^{R**}\right){\text{e}}^{-\left(\frac{2\mu +{\rho }^2-\rho A}{2{\phi }^2}-\mu \right)t}\\ N_Y^{R*}=\left(\phi N_0-N^{R**}\right){\text{e}}^{-\left(\frac{2\mu +{\rho }^2-\rho A}{2{\phi }^2}-\mu \right)t}+\frac{b_5^{R*}{\phi }^2}{2{\phi }^2{b}_4^{R*}-c\mu }\end{array}$ (53)

其中：

$p_d^{R**}=\frac{\left(-1+\lambda \right)\left(2+2m-2\alpha -m\alpha \lambda \right)}{B}+\frac{4m\left(-2+\lambda \right)\left(-1+\lambda \right)\lambda L{\phi }^2}{c{B}^3{\rho }^2\left(A^2-1\right)}$， $N^{R**}=\frac{b_5^{*}{\phi }^2}{2{\phi }^2{b}_4^{*}-c\mu }$

$p_e^{R**}=\frac{2\alpha \left(-1+\lambda \right)+m\left(-2+\lambda +\alpha \lambda \right)}{4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2}-\frac{8\left(1+m\right)\left(-1+\lambda \right)\lambda L{\phi }^2}{c{B}^3{\rho }^2\left(A^2-1\right)}$， $s_{}^{R**}=-\frac{4\lambda L\left(\mu +\rho -\rho A\right)}{c{B}^2{\rho }^2\left(A^2-1\right)}$，

$A=\frac{1}{\rho }\sqrt{{\left(2\mu +\rho \right)}^2-\frac{16\left(1+m\right)\left(-1+\lambda \right)\lambda \left(2\left(-1+\lambda \right)+4m\left(-1+\lambda \right)+m^2\lambda \right){\phi }^2}{c{B}^2}}$

$B=4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2$

$L=8\alpha {\left(-1+\lambda \right)}^2+4m\left(1+5\alpha \right){\left(-1+\lambda \right)}^2+4m^2\left(-1+\lambda \right)\left(-2-2\alpha +2\lambda +3\alpha \lambda \right)+m^3\lambda \left(-4+\left(3+\alpha \right)\lambda \right)>0$

为了使系统在计划期内收敛，需要满足以下条件： $0<A<1$

证明同命题12。

推论4：在佣金模式下，品牌商的直播价格和直销价格、网红的直播服务水平以及网红直播引流量会随着直播渠道规模比例的变化而变化，即：

$\frac{\partial p_e^{R**}}{\partial \alpha }\{\begin{array}{ll}>0\hfill & \lambda \in \left[0,\frac{2}{2+m}\right]\hfill \\ <0\hfill & \lambda \in \left[\frac{2}{2+m},\frac{2+4m}{2+4m+m^2}\right]\hfill \end{array}$， $\frac{\partial p_d^{R**}}{\partial \alpha }<0$， $\frac{\partial s^{R**}}{\partial \alpha }>0$， $\frac{\partial N^{R**}}{\partial \alpha }<0$ (54)

由推论4可知：

1) 当 $\lambda \in \left[0,\frac{2}{2+m}\right]$ 时，产品的直播价格随着直播渠道需求比例的扩大而提高；当 $\lambda \in \left[\frac{2}{2+m},\frac{2+4m}{2+4m+m^2}\right]$ 时，产品的直播价格随着直播渠道需求比例的扩大而降低。

由式(54)可以求得 $\frac{\partial p_e^{**}}{\partial \alpha }=\frac{-2+\left(2+m\right)\lambda }{4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2}$。当 $\lambda \in \left[0,\frac{2}{2+m}\right]$ 时， $\frac{\partial p_e^{R**}}{\partial \alpha }>0$，即直播渠道需求比例越大，产品的直播价格越大；当 $\lambda \in \left[\frac{2}{2+m},\frac{2+4m}{2+4m+m^2}\right]$ 时， $\frac{\partial p_e^{R**}}{\partial \alpha }<0$，即直播渠道需求

比例越大，产品的直播价格越小。也就是说，当网红主播的分成比例较小时，直播渠道需求比例越大，品牌商更愿意提高产品直播价格来获利；而当网红主播的分成较大时，直播渠道需求比例越大，品牌商更愿意牺牲直播价格来扩大需求，实现利润最大。理论上，只有 $\lambda$ 非常接近1时，才会出现这种状况，但是现实中数据调查显示，网红主播的佣金比例大约处于5%~30%之间，不会出现佣金比例接近1的情景。

2) 品牌商的直销价格总是随着直播渠道市场规模比例的扩大而降低，也就是说，品牌商总是希望通过降低价格来获利。

由式(54)可得 $\frac{\partial p_d^{R**}}{\partial \alpha }=-\frac{\left(-1+\lambda \right)\left(2+m\lambda \right)}{4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2}<0$，当直播渠道需求比例较大时，品牌商总是降低产品的直销价格以提高产品需求来获利。

3) 网红主播的直播服务水平随着直播渠道市场规模比例的扩大而提高。

由式(54)知 $\frac{\partial s^{R**}}{\partial \alpha }=\frac{2\lambda \left(8{\left(-1+\lambda \right)}^2+20m{\left(-1+\lambda \right)}^2+m^3{\lambda }^2+4m^2\left(-1+\lambda \right)\left(-2+3\lambda \right)\right)\phi }{c{\left(4\left(-1+\lambda \right)+8m\left(-1+\lambda \right)+m^2{\lambda }^2\right)}^2\rho \left(1+A\right)}>0$，随着直播渠道需求比例的扩大，网红主播的直播服务水平总是被激励。

推论5：在佣金模式下，品牌商的直播价格和直销价格、网红的直播服务水平以及网红直播引流量会随着网红直播服务成本系数的变化而变化，即：

$\frac{\partial p_e^{R**}}{\partial c}>0$， $\frac{\partial p_d^{R**}}{\partial c}>0$， $\frac{\partial s^{R**}}{\partial c}<0$， $\frac{\partial N^{R**}}{\partial c}<0$ (55)

推论5表明，网红的直播服务成本系数会对网红的直播服务水平和直播引流量产生影响，进而影响产品的直销价格和直播价格。当直播服务成本系数越大，其直播成本将越大，因此网红将降低直播服务水平来实现利润最大化，二者之间呈负相关。另外，直播引流量的变化与网红直播服务水平呈正相关，直播服务成本系数的变化也将间接影响直播引流量的变化，并也呈现负相关变化趋势。对于品牌商而言，当网红直播服务成本较高时，品牌商应当提高产品的直播价格和直销价格以实现利润最大化。因为佣金模式下，品牌商需将直播渠道下的利润以一定的佣金率分配给网红，此种模式需实现直播渠道利润最大化，同时也将实现二者的利润最大化，网红直播服务成本系数的提高会导致供应链中成本的增加，因此产品的价格也将随之而有所提高。

由于不同渠道模式下，品牌商和网红主播的利润最优值函数的复杂性，无法用解析的方式进行证明分析，本文将在下一节采用数值模拟来求证。

5. 数值分析

本节将借助数值模拟，进一步分析验证系统参数的变化对品牌商渠道模式选择和价格决策以及网红主播价格和服务决策的影响。基本参数值的选取基于的Lu [13] 的研究，并进行相应调整以满足模型假设条件，具体设置如下： $\alpha =0.2;c=0.8;\lambda =0.2;\mu =0.01;m=0.3;\rho =0.6;\phi =0.5;G_0=0.4$ ；本文利用通过mathmatics实现。

5.1. 产品直播价格和网红主播服务努力程度的最优路径分析

单一渠道模式下，品牌商只可以选择线上直销或者线上直播模式进行销售。当品牌商选择线上直播时，通过借助网红主播的直播影响力来引流，进而扩大产品需求。不同策略下，产品的直播价格和网红主播服务努力水平的最优路径如图1(a)和图1(b)所示。双渠道模式下，品牌商同时选择线上直销和线上直播进行销售，品牌商和网红主播间不同策略下，产品的直播价格和网红主播的服务努力水平最优路径如图1(c)和图1(d)所示。

从图1可知，无论何种策略下，产品的直播价格和网红主播的服务努力程度都将随着时间的推移而达到稳定状态，且与网络的基本引流量无关。同时，可以看出，无论是单渠道模式还是双渠道模式下，品牌商和网红主播佣金策略下的产品稳态直播价格会低于加价策略下的稳态价格。

(a) (b)(c) (d)Figure1. The path map of the best live product price under Single Channel/Dual Channels图1. 单/双渠道下最优产品直播价格和直播服务水平路径图

5.2. 网红主播影响力对产品直播价格的影响分析网红主播可通过自身的影响力，扩大产品的市场需求，起到一定的引流效果，从而会对品牌商和网红主播的价格和服务努力决策产生影响。图2刻画了不同渠道策略下网红主播的影响力对产品的直播价格的影响。从图2可知，无论何种策略下，产品的直播价格均随着网红主播影响力的提高而降低，相对加价模式，佣金策略下产品的直播价格较低。这是由于网红主播的影响力较大意味着引流量的初始值也将处于高位，对产品的需求影响较高，品牌商也愿意为提高产品需求而降低价格。这也可以说明在现实中，为什么影响力较大的网红主播具有一定的议价能力，可以与品牌产品谈到一个较低的价格。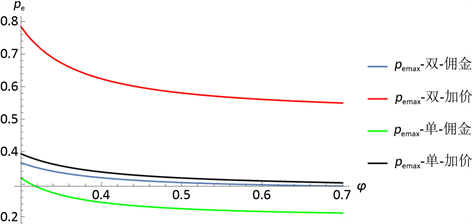

Figure 2. The influence of anchor influence on the price of live product r

图2. φ对产品直播价格的影响

5.3. 最优利润值分析

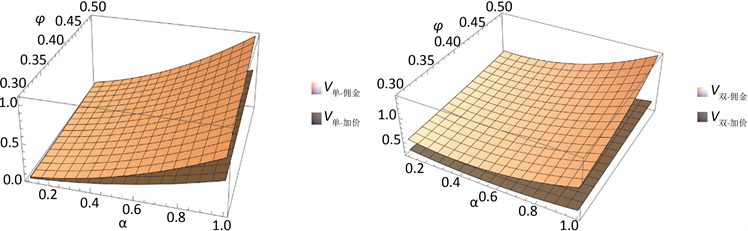(a) (b)

Figure 3. The Influence of α and m on the Profit of Supply Chain under Single/Dual Channels

图3. α和m对单渠道供应链整体利润的影响

如图3(a)和图3(b)所示，网红“佣金”模式下供应链整体的利润始终要高于网红“加价”模式下的供应链整体利润。单渠道模式，随着直播时长比例需求的增大，供应链整体的利润也随之增大。双渠道模式下，供应链整体的利润先随着直播市场比例的增大而减小，当直播市场需求比例超过某一值时，供应链整体利润将随之而增大，呈现正比例上升趋势。这是因为当直播市场需求比例较小时，供应链中直销渠道占据优势，获利较大，网红主播的直播低价策略会降低整体的利润。当直播市场需求比例大于某一值时，直销渠道不再占据优势，网红主播将更愿意提高服务努力程度来提高引流量，从而提高供应链整理的利润，且网红“佣金”模式下的供应链整体利润要高于网红“加价”模式下的供应链利润。

6. 结论与展望

直播电商的进入为市场打开了新的通道，网红主播的参与是否会为市场带来新的生机，品牌商与网红主播之间又应采取何种模式策略已成为了大家共同关注的问题。本文考虑网红主播的影响力，探究线上品牌商是否进入直播电商以及应与网红主播采取如何合作实现利润最优。本文主要关注品牌商与网红主播间的“加价”和“佣金”两种合作模式，考虑网红主播动态引流量的影响，从单渠道和双渠道角度出发，分别探究两种不同模式下品牌商和网红主播的均衡策略和利润，进一步分析网红主播影响力和直播市场需求比例对品牌商的均衡决策以及其直播服务努力程度的影响。研究发现：

1) 当品牌商引入网红直播渠道时，无论采取何种模式，网红主播的直播服务努力程度均随时间而单调变化，且取决于网红主播的初始引流量以及稳态网红主播引流量之间的差距。同时，品牌商和网红主播的均衡动态定价策略也受到网红初始引流量和稳态引流量的影响。当网红主播的影响力较大，初始引流量大于稳态均衡引流量时，网红主播的直播服务努力程度随着引流量的增加而降低，品牌商和网红主播采取价格撇除策略，即随着时间的推移，降低产品的批发价和网红加价价格；反之亦反。

2) 无论何种渠道下，产品的直播价格与网红主播的影响力成反比，网红主播的直播服务努力与网红主播的影响力成正比。当网红影响力越大时，网红主播的直播引流量越大，产品的直播需求量越大，网红的议价能力也将会有所体现，故产品的直播价格会随之降低。另外，当网红主播的影响力越大，其单位直播服务努力所带来的边际效益越大，加之产品直播价格的降低，均激励网红主播提高其直播服务努力程度。此外，采取网红“佣金”模式时的产品直播价格均会低于采取网红“加价”模式下的产品直播价格，而其直播服务努力程度也较高。

3) 直播市场需求比例会对品牌商和网红主播的策略产生影响。当直播市场需求比例较大时，意味着直播市场具有较大潜力，网红主播更愿意提高直播服务努力程度；品牌商会随着直播需求比例的提高而降低产品的直销价格，提高产品的直播价格。该结论表明，在直播市场需求比例较高时，网红主播的直播服务努力程度会被激励，品牌商更倾向于直播渠道中提高直播价格，直销渠道中降低直销价格来获取更大的利润。

4) 网红“佣金”模式下供应链整体的利润要高于网红“加价”模式下的供应链整体利润。随着直播市场需求比例的扩大，双渠道下供应链整体利润先减少后增大。直播市场需求比例过小，其低价策略会使得整体利润下降，当直播市场比例较大时，产品的直播将有所提高，网红主播的引流优势也将会突显，从而供应链整体利润上升。这也侧面说明在刚刚开通直播渠道时，直播市场比例较小，供应链整体利润是呈现下降趋势，但是一旦打通直播渠道，具备一定的“粉丝”基础，供应链的整体利润将会有所提高，这也是为什么许多直销店铺要开通直播间的原因。现实中许多网红店铺就是先吸引粉丝，具备一定流量后，直播卖货并取得了较好的成效。只要能够合理的制定分配比例和坑位费，品牌商和网红主播便能实现“双赢”的局面。

目前本文存在一定的局限性，仅考虑了网红主播在直播渠道的动态引流量，未来可以在研究中考虑直播渠道下网红引流量的溢出效应，以更加的贴近现实，为直播电商及网红主播是否进入市场提供一定的参考价值。