基于MATLAB的自锚式悬索桥空间主缆找形计算分析

Form Finding Calculation and Analysis of Space Main Cable of Self Anchored Suspension Bridge Based on MATLAB

摘要: 本文阐述了自锚式悬索桥空间主缆线形计算方法和空间主缆MATLAB程序开发思路，结合分段悬链线理论为依据编制的解析法计算程序，利用有限元法程序建立某自锚式悬索桥完整的成桥模型。结合某一实际自锚式悬索桥空间主缆找形，通过数值计算法结合有限元计算法解决自锚式悬索桥空间主缆成桥找形，精度满足施工要求。利用求得的主缆无应力长度建立空缆模型，用于后续施工过程模拟，对后续施工中主缆、吊杆下料长度计算，主缆挂设控制，索夹的安装预偏，吊杆的张拉方案等工作有着重要的指导意义。

Abstract: This paper describes the calculation method of spatial main cable shape of self anchored suspension bridge and the development idea of spatial main cable MATLAB program. Combined with the analytical method calculation program compiled based on the segmented centenary theory, a complete bridge model of a self anchored suspension bridge is established by using the finite element method program. Combined with the form finding of the spatial main cable of a practical self anchored suspension bridge, the form finding of the spatial main cable of the self anchored suspension bridge is solved by numerical calculation method and finite element calculation method, and the accuracy meets the construction requirements. The unstressed length of the main cable is used to establish an empty cable model, which is used for the simulation of the subsequent construction process. It has an important guiding significance for the calculation of the blanking length of the main cable and the suspender, the control of the main cable hanging, the pre-deflection of the cable clamp installation, and the tensioning scheme of the suspender in the subsequent construction.

1. 引言

现代交通日益发达的背景之下，桥梁作为国家交通建设的重要组成部分，其建设受到了越来越多的重视，国家也在全力支持桥梁的发展。所以近些年来，我国新建桥梁的跨度一次次创下新高，桥面宽度也不断增大，同时桥梁的形式也日益丰富。目前桥梁主要的结构形式包括梁桥、拱桥、斜拉桥、悬索桥等等，而悬索桥以其优美的外形，合理的受力结构得到了广泛的运用。无论是作为城市中的景观桥梁还是作为跨越大河或者连接两座山的重要纽带，我们都能看到悬索桥的身影。悬索桥又分为自锚式悬索桥和地锚式悬索桥，自锚式悬索桥以其自身独特的一些优势，在很多地方被采用。

自锚式悬索桥的成桥状态包括体系各部分的内力和线形，它们对悬索桥设计和施工控制尤为重要。其中，吊索索力和主缆线形是最重要的两个状态指标，吊索索力是求解主缆线形的基础，也决定了自锚式悬索桥加劲梁的内力分布。很多国内外学者对确定自锚式悬索桥索力展开研究，提出了梁段重量法、刚性支撑连续梁法、弯曲应变能最小法、影响矩阵法等多种方法 [1]。随着桥梁建设水平的提高，悬索桥计算理论由平面缆索向空间缆索过渡，计算方法不断向更精细、更高效的目标发展。

2. 自锚式悬索桥主缆线形计算方法

悬索桥成桥状态时主缆不仅承受沿弧长分布的均布荷载q (例如主缆自重，主缆缠丝及防护，主缆检修道)，还承受吊索传递来的集中荷载Pi的作用(例如索夹，吊索自重及其传递来的加劲梁恒载，锚具自重等) [2]，因此需要引入分段悬链线理论进行主缆成桥状态的线形分析，此时主缆受力示例图如图1所示。

将主缆分成n段，满足下列力学条件：

$\begin{array}{l}{H}_L^1=-H_R^1=H_L^i=-H_R^i\\ V_R^i=q{S}_0^i-V_L^i=P_i-V_L^{i+1}={\displaystyle \underset{k=1}{\overset{i}{\sum }}q{S}_0^k}+{\displaystyle \underset{k=1}{\overset{i-1}{\sum }}{P}_k-V_L^1}\end{array}$ (1)

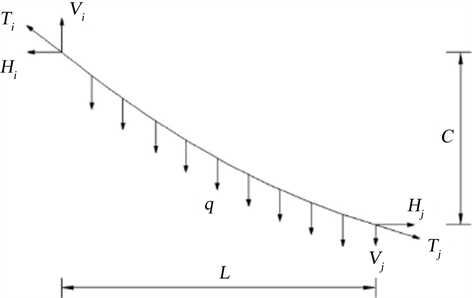
Figure 1. Diagram of main cable stress in section catenary theory

图1. 分段悬链线理论主缆受力示意图

当主缆其中一端的水平分力、竖直分力以及各段的无应力长度已知时，即已经给出H、V和S₀的值时，可以将这些值代入到式(1)中，能够轻易求出主缆的跨度L和高差C，那么也得出了此跨主缆的线形。在已知主缆无应力长度求解空缆状态线形时可以利用此方法计算。

当主缆其中一端的水平分力、竖直分力以及跨度已知时，即已经给出H、V和L的值时，求解非线性方程组的具体方法如下：

1) 根据抛物线理论计算出主缆的水平分力的初值H₀和竖直分力的初值V₀如下：

$H_L^1=\frac{\omega l^2}{8f},V_L^1=\frac{\omega l}{2}+H_L^1\frac{C}{L}$ (2)

2) 利用牛顿迭代法计算出主缆第一段的无应力长度：

$\left[\frac{H_L^{i+1}}{V_L^{i+1}}\right]=K^{-1}\left[\frac{\Delta l_i}{\Delta c_i}\right]+\left[\frac{H_L^i}{V_L^i}\right]$ (3)

式(3)表明了主缆的跨度和高差变化量与内力变化量之间的关系，即为水平分力初值和竖直分力初值的修正公式。

3. 基于MATLAB空间主缆找形

空间缆悬索桥是一种由主缆和吊杆组成的、复杂的三维几何体系。相较平面缆来说，它具有竖向承载能力相当、而横向刚度和抗扭刚度更大的特点，但其设计计算难度则远远高于平面缆。主缆空缆状态的线形计算目前一般采用的是基于分段悬链线分析理论的解析法，该方法的参数变量容易控制，运算速度快，计算结果精度高，能够很好地满足设计要求。此方法是基与主缆的无应力长度不变的性质和主缆的质量守恒，以成桥状态计算出的主缆无应力长度，各个索鞍的初始位置，主缆截面特性和初始锚固点的坐标等作为初始条件，采用与主缆成桥线形相同的计算逻辑，通过悬链线方程进行各跨内每个索段的循环，判断另一端点的坐标是否与控制点坐标相符，如相符就说明假定的索端水平力，竖向力值正确，否则需要修正假定的初值重新计算，直到满足收敛精度 [3]。

成桥状态时塔顶两侧的主缆水平分力是一样的，因此塔顶不发生偏移且塔底没有弯矩，因此索鞍在成桥状态时没有剪力。而在空缆状态下，主缆没有外荷载作用(如吊索力，索夹重量等)，只有自重，由于主塔两侧主缆不是完全对称的，因此空缆状态下塔顶主缆水平分力大小不一致，若此时索鞍仍按照成桥位置安装，将会产生很大的不平衡力，这些力需要主塔来承担，这样可能会产生需要较大张拉力、主缆架设精度难以满足、主塔偏移等几种不利的情况，提高工程造价，增加施工难度。

在计算自锚式悬索桥主缆空间线形时，需要计算成桥状态下的主缆无应力索长，锚固点的位置坐标已经给出，即此时的几何边界条件已知。目前市场上已知的商用软件如Midas Civil等，仅涉及悬索桥平面缆找形计算 [4]。基于此，本文设计与开发便于工程师应用的悬索桥空间主缆找形MATLAB程序。程序基本流程如图2所示：

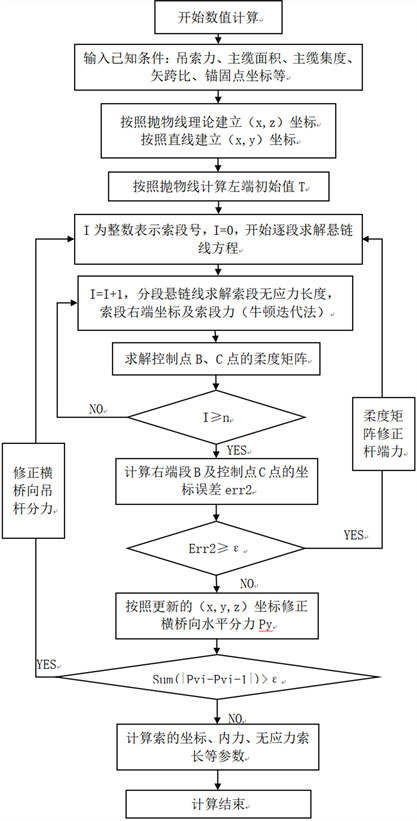
Figure 2. Basic operation flow chart of space main cable form finding MATLAB program

图2. 空间主缆找形MATLAB程序基本操作流程图

4. 工程案例

黄河特大桥主桥为独塔自锚式悬索桥，为提高悬索桥整体刚度，增加1对斜拉索，跨径布置为50 + 350 + 350 + 50 = 800 m。整体上采用先梁后缆施工方法。主梁为分离式钢箱梁全宽47 m，桥塔采用独柱型。主缆为空间线形，布置在钢箱梁两侧。将大北环特大桥主桥桥梁参数整理成固定格式带入MATLAB编写开发的程序，计算主缆的无应力索长、主缆的控制点的坐标参数、采用计算的坐标计算吊杆的无应力索长。将MATLAB建模计算参数带入Midas Civil进行迭代计算。主塔、主梁、主缆的位移如图3所示，将悬索桥数值计算的程序带入Midas迭代计算位移基本为零，成桥状态是稳定的。

Figure 3. Member displacement diagram

图3. 构件位移图

根据主缆无应力长度不变的性质以及主缆空缆线形的计算方法，利用解析法对该大桥的空缆线形进行计算，黄河特大桥空缆状态下主缆的各吊索点的坐标如表1所示。

Table 1. Main cable empty cable state alignment

表1. 主缆空缆状态线形

选择1~20号吊杆，导入MATLAB进行数值计算；计算得到无应力索长LS₀，每个吊杆节点的三维坐标(X_P, Y_P, Z_P)；每个节点横向分力P_y等数据。按照基本数据在Midas Civil进行建模，将MATLAB计算数据(X_P, Y_P, Z_P)导入Midas Civil，进行建模，无应力索长LS₀带入Midas Civil；主缆的竖向P_z和横向力P_y均带入Midas Civil。Midas Civil节点、单元、荷载等均要和MATLAB保持一致。利用Midas civil进行非线性计算分析，吊杆变形量如图4所示，可以看出Midas Civil迭代计算位移接近于零，误差满足施工精度要求。

Figure 4. Hanger deformation diagram

图4. 吊杆变形图

由图4可知，通过理论计算的成桥主缆线形和有限元仿真计算出的成桥主缆线基本一致，绝大多数控制点高差均在0.33 mm之内，相比于350 m的总跨度，可以认为理论计算线形和有限元计算线形相同。由此说明本文所提出的主缆线形的MATLAB嵌套精细化计算方法的准确性，同时也说明了所建立有限元模型的正确性。

5. 结语

主缆线形作为自锚式悬索桥的关键部位，其自身受力的安全性以及传力的可靠性往往决定设计的成败。本文通过对空间主缆线形的理论分析，及某一具体实际桥梁进行有限元模拟分析，采用数值计算法综合有限元计算法，解决了自锚式悬索桥空间主缆成桥找形的难题。本文所采用的分析方法和所得结论为该自锚式悬索桥主缆找形的构造设计提供了指导性依据，并供同类型桥梁设计参考。