1. 引言
近年来国家交通建设发展迅速，城市地铁、地下通道等隧道为人们的生活提供了极大的便利，但随着地下隧道开挖深度的加大，隧道围岩环境也愈发复杂。围岩侧压系数作为影响隧道围岩环境的一个重要指标，对隧道、巷道等地下工程中的围岩稳定性有着重要的影响。国内外众多学者针对隧道开挖过程中围岩的变形规律开展了多方面的研究，在采用经验公式法 [1] [2] 、模型试验法 [3] [4] 等研究手段的基础上，总结分析了多种条件下的隧道变形规律，为解决隧道开挖过程中的沉降变形问题及变形预警预测提供了理论依据。方超等 [5] 利用ABAQUS软件，研究了在不同侧压力系数下围岩的变形规律和支护措施的力学响应规律；余莉等 [6] 通过对高地应力地区隧道围岩分级研究，指出了在高地应力隧道中侧压力系数对隧道稳定性有着重要的影响；李仲奎 [7] 提出了适用于深埋隧道数值模拟初始地应力场生成的方法，研究成果可为采用数值模拟手段分析围岩稳定性规律提供参考。
上述学者在隧道围岩稳定性研究方面进行了深入探讨，取得了众多卓有成效的研究成果。但是，通过对隧道稳定性研究现状的总结可以发现：在利用数值模拟软件进行隧道开挖的模拟时，较少有学者提及初始应力场的响应问题，而以侧压力系数为代表的地应力场分布情况却直接影响隧道开挖后围岩的稳定性。为此，本文结合三维有限差分数值模拟软件FLAC3D，分析不同侧压力系数对隧道开挖稳定性的影响规律，以期在总结相关规律的基础上，为相似地质条件下隧道开挖过程中的围岩支护提供理论依据。
2. FLAC3D简介
FLAC3D [8] 是由美国Itasca公司研发推出的有限差分数值分析软件，适用于建立三维连续介质模型用以模拟三维岩土体及其他介质中工程结构的受力与变形状态，广泛应用于边坡工程、釆矿工程、地下洞室、岩土工程等多个领域，并已被公认为进行岩土力学数值模拟研究行之有效的方法之一。
FLAC3D [9] 程序是建立在拉格朗日算法基础上，特别适合模拟大变形和扭曲。FLAC3D采用显式算法来获得模型全部运动方程(包括内变量)的时间步长解，从而可以追踪材料的渐进破坏和垮落，这对研究边坡设计是非常重要的。FLAC3D程序具有强大的后处理功能，用户可以直接在屏幕上绘制或以文件形式创建和输出打印多种形式的图形，还可根据需要将若干个变量合并在同一图形中进行研究分析。
3. 数值模拟建立
3.1. 数值模型
以某地下直墙半圆拱形隧道模型为例，建立数值模型，直墙半圆拱隧道由矩形与半圆组成，其中半圆部分的半径为2 m，直墙部分高度为2 m、隧道底部长度为4 m，按照矩形部分的0.5 m间隔划分网格。采用FLac3D软件建立隧道二维数值模型，对应模型尺寸：x * y * z = 50 m * 1 m * 80 m，数值模型如图1所示，所选取的围岩物理力学参数如表1所示。
Table 1. Model physical and mechanical parameters
表1. 模型物理力学参数
在FLAC3D模型计算中，围岩中采用的是摩尔–库伦(Mohr-Coulomb)弹塑性材料模型，在岩石力学计算分析中相关的模量参数有剪切模量、体积模量等，这些参数可根据弹性力学中的计算公式(式1)换算求得 [10] ：
(1)
式中：k为体积模量、E为弹性模量、G为剪切模量、μ为泊松比。
为进一步探究隧道在开挖过程中的位移及塑性区等变化规律，在隧道顶、底及两侧位置处设立监测点A、B、C、D (如图2所示)，隧道开挖后提取监测点的垂直位移、水平位移等相关数据进行分析。
3.2. 边界条件
模型的上、下(z = −40 m、z = 40 m)；左、右(x = −25 m、x = 25 m)；前、后(y = 0 m、x = 1 m)六个面皆为固定位移边界，以模型原点位置处所在位置的垂直应力szz = 10 MPa为基准，按照垂直应力梯度22000 Pa/m定义整个模型垂直应力的初始值，不同侧压力系数可通过改变szz、sxx、syy的初始值及梯度比例关系进行反演，当侧压力系数λ = 1 m时，在FLAC3D数值模拟软件可用如下形式表达：szz = sxx = syy = 10 MPa，sxxgrad = syygrad = szzgrad = 22000 Pa/m。
3.3. 结果分析
在隧道开挖过程中，采用巷道模型一次挖空的方法进行处理。计算采用摩尔–库伦(Mohr-Coulomb)弹塑性材料模型。下面以不同侧压力系数λ影响下，隧道开挖后塑性区、监测点垂直位移、水平位移演化规律作为研究对象，取侧压力系数λ分别为：1、1.5、2、2.5为研究条件。
3.3.1. 塑性区演化规律分析
隧道施工开挖时因为周边土体会产生应力重分布，可能会导致围岩造成屈服破坏而产生塑性区。依据已得到研究内容可以获得，塑性区大小对围岩稳定性具有关键影响，与围岩的应力尺寸、岩土体的特性密切相关，因此塑性区产生的影响在研究围岩稳定性时不容忽视。本实验中分别取侧压力系数为1、1.5、2、2.5作为研究条件，隧道开挖后不同侧压力系数条件下塑性区的云图如图3所示：
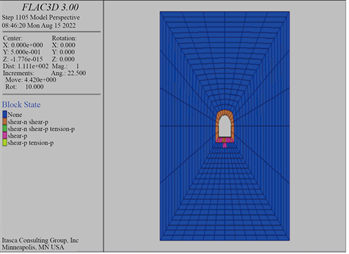
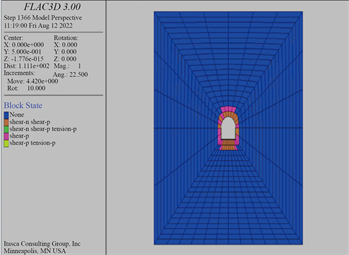λ = 1 λ = 1.5
λ = 2 λ = 2.5
Figure 3. Nephogram of plastic zone after tunnel excavation under different lateral pressure coefficients
图3. 不同侧压力系数条件下隧道开挖后塑性区云图
由图3可以看到，在其余条件保持不变的情况下，当侧压力系数λ分别为：1、1.5、2、2.5时，对应围岩的塑性区范围分别为：2 m、4 m、6 m、12 m，即表明随着侧压力系数λ的增大，隧道开挖后围岩塑性区云图范围呈现不断增大趋势，且增长率不断增大。
当侧压力系数为1时，可以看到此时整个隧道的开挖区塑性范围比较小，并且隧道边墙塑性区范围比隧道顶部塑性区范围大。当侧压力系数增加到2.5时隧道的开挖区塑性范围明显增大且向拱顶处扩大，且此时的水平应力是要大于垂直应力的。
以上研究表明：在其余条件不变的情况下，侧压力系数越大、隧道开挖之后围岩不稳定且不稳定区域集中在拱顶、拱底与拱肩处，此时应采取有效加固措施，以防止围岩发生较大变形。
3.3.2. 垂直位移演化规律
为进一步探究不同测压系数影响下围岩变形特征，以拱顶点A、拱底点B监测数据为依据，探究垂直位移随侧压力系数变化规律，以λ = 1、2时拱顶监测点A垂直位移随计算时间步数变化关系为例说明，对应监测点A处垂直位移随模拟中的计算步数变化关系如图4、图5所示。
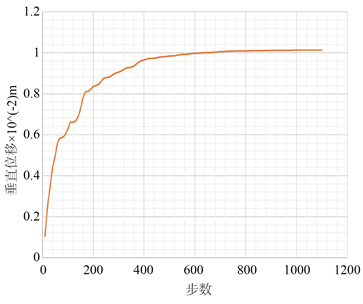
Figure 4. The vertical displacement curve of point A (λ = 1)
图4. λ = 1时监测点A的垂直位移曲线
Figure 5. The vertical displacement curve of point A (λ = 2)
图5. λ = 2时监测点A的垂直位移曲线
由图4、图5中曲线变化规律可知随着计算时间步数的增加，检测点A垂直位移量逐渐增加然后趋于平衡，最终的平衡值则是隧道开挖后检测点的最终垂直位移量，据此可得λ = 1时垂直位移量为1.01 cm；λ = 2时垂直位移量为1.98 cm，同时可以看出垂直位移曲线均有几处明显的突变点，且随着时间计算步数的增加，突变点越明显，说明当时间计算步数变大，隧道拱顶位移量变大，且拱顶在应力释放时位移会突然发生变化。对其余监测点进行垂直位移随计算时间步数变化数据提取也得到同样的规律。
由λ = 1、2为例得出变化规律，遂以λ = 1、1.5、2、2.5得出垂直位移随侧压力系数变化规律如图6所示，当侧压力系数分别为1、1.5、2、2.5时，对应隧道顶部监测点垂直位移分别为：1.01 cm、1.32 cm、1.98 cm、2.63 cm，即随侧压力系数的增大，垂直位移也逐渐增大，且增长趋势也在增大。同时对比拱顶A点和拱底B点进行横向比较，如图6、图7所示，图7中当侧压力系数分别为1、1.5、2、2.5时，对应隧道底部监测点垂直位移分别为：1.51 cm、1.82 cm、2.48 cm、3.13 cm，均表明在拱顶、拱底垂直位移均随侧压力系数增大而增大，且斜率逐渐增大。得出结论：在其余条件保持不变的条件下，无论在任何监测点，垂直位移均随侧压力系数增加而增加。
Figure 6. The relationship between vertical displacement and lateral pressure coefficient (A)
图6. 垂直位移随侧压力系数变化关系(A)
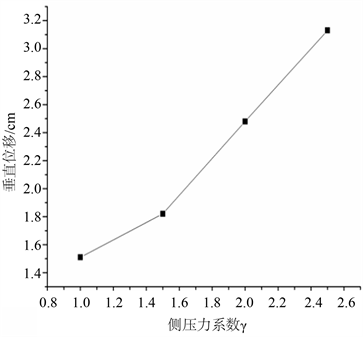
Figure 7. The relationship between vertical displacement and lateral pressure coefficient (B)
图7. 垂直位移随侧压力系数变化关系(B)
3.3.3. 水平位移演化规律
为进一步探究不同测压系数影响下围岩变形特征，以边墙点C、D监测数据为依据，探究水平位移随侧压力系数变化规律，以λ = 1、2时边墙监测点C水平位移随计算时间步数变化关系为例说明，对应监测点C处水平位移随模拟中的计算步数变化关系如图8、图9所示。
Figure 8. The horizontal displacement curve of point C (λ = 1)
图8. λ = 1时监测点C的水平位移曲线
由图8、图9中曲线变化规律可知随着计算时间步数的增加，检测点C的水平位移量逐渐增加然后趋于平衡，位移曲线突变点逐渐消失，最后趋于稳定，最终的平衡值则是隧道开挖后检测点C的最终水平位移值，据此可得λ = 1时最终水平位移量为0.99 cm，λ = 2时最终水平位移量为2.73 cm。当时间计算步数较小时拱腰处的监测点C位移变化量也相对于时间计算步数增大后的位移变化量较小。对其余监测点进行水平位移随时间计算步数变化数据提取也得到同样的规律。
Figure 9. The horizontal displacement curve of point C (λ = 2)
图9. λ = 2时监测点C的水平位移曲线
由λ = 1、2为例得出变化规律，遂以λ = 1、1.5、2、2.5得出水平位移随侧压力系数变化规律如图10所示，当侧压力系数分别为1、1.5、2、2.5时，对应隧道监测点C水平位移分别为：0.99 cm、1.72 cm、2.73 cm、4.05 cm，即随侧压力系数的增大，水平位移也逐渐增大，且增长趋势也在增大。提取监测点C、D水平位移数据进行横向比较，如图10、图11所示，图11中当侧压力系数分别为1、1.5、2、2.5时，对应隧道边墙监测点D水平位移分别为：0.99 cm、1.72 cm、2.73 cm、4.05 cm，均表明在其余条件保持不变的情况下，随着侧压力系数增大，隧道边墙监测点处的水平位移也表现出相应增加，且增长率呈现不断增大趋势。得出结论：在其余条件保持不变的情况下，在任何监测点水平位移均随侧压力系数增大而增大。
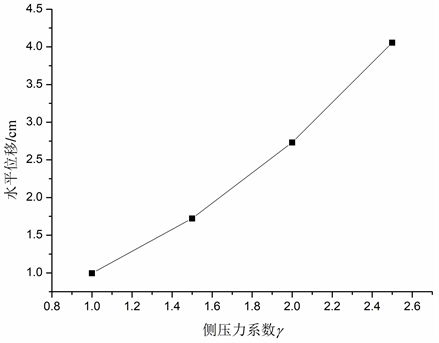
Figure 10. The relationship between horizontal displacement and lateral pressure coefficient (C)
图10. 水平位移随侧压力系数变化关系(C)
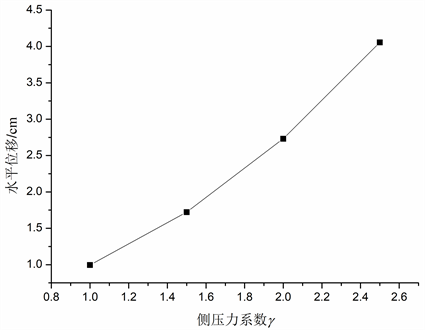
Figure 11. The relationship between horizontal displacement and lateral pressure coefficient (D)
图11. 水平位移随侧压力系数变化关系(D)
4. 结论
通过运用FLAC3D有限差分软件建立隧道模型，研究不同测出压力系数的条件下隧道开挖后塑性区分布规律和围岩变形规律，所取得主要结论如下：
1) 在其余条件保持不变的情况下，当侧压力系数λ分别为：1、1.5、2、2.5时，对应围岩的塑性区范围分别为：2 m、4 m、6 m、12 m，即表明随着侧压力系数λ的增大，隧道开挖后围岩塑性区云图范围呈现不断增大趋势，且增长率不断增大。
2) 侧压力系数分别为1、1.5、2、2.5时，对应隧道顶部监测点A垂直位移分别为：1.01 cm、1.32 cm、1.98 cm、2.63 cm，因此在其余条件保持不变的情况下，随着侧压力系数增大，隧道顶部相同位置处的垂直位移也相应增加，且近似呈现正比关系。
3) 侧压力系数分别为1、1.5、2、2.5时，对应隧道边墙监测点C水平位移分别为：0.99 cm、1.72 cm、2.73 cm、4.05 cm，因此在其余条件保持不变的情况下，随着侧压力系数增大，隧道边墙位置处的水平位移也表现出相应增加，且增长率呈现不断增大趋势。
侧压系数是对于隧道的稳定性有重要的作用，在施工初期应该重视侧压系数对围岩稳定性的影响。在不同侧压系数条件下进行隧道开挖会形成不同程度的塑性变形，隧道围岩会发生一定的变形以释放部分压力，从而维持围岩的稳定性，对于性质较差的岩体会发生一定的破坏，以拉张性破坏和剪切破坏为主。应根据不同围岩的成分选择合适的支护形式进行保护，确保围岩的稳定性和隧道开挖的安全性。
基金项目
宿州学院大学生创新创业项目ZCXM22-327。
NOTES
*通讯作者。