基于混合算法优化BP-PID控制的负压吸引器研究

Research on Negative Pressure Aspirator Based on Hybrid Algorithm to Optimize BP-PID Control

摘要: 负压伤口治疗技术(Negative Pressure Wound Therapy, NPWT)是一种创面治疗新技术，负压吸引器应用该技术广泛应用于临床伤口愈合治疗中。真空泵作为负压源是主要的工作部件，针对其存在外部干扰、传感器延迟以及建模不精确等引起的负压强度不稳定的现象，提出一种应用于真空泵的连续负压控制优化方法。首先，提取真空泵及导管等的关键参数，建立负压吸引器创面治疗过程中的数学模型；其次，结合BP神经网络和PID控制，通过识别并优化真空泵伺服动态控制参数，并反馈到控制器输入端；最后，引入灰狼算法(GWO)与粒子群算法(PSO)的混合算法优化BP神经网络，进一步提高神经网络的精度。通过仿真，与传统PID、BP-PID及PSO-BP-PID相比，所提出的混合算法分别提前了1.0s 、0.5 s和0.4 s，稳态误差分别减少了98%、90%和80%，且几乎无振荡和超调，并通过实验验证了应用于负压吸引器上有良好的控制效果。

Abstract: Negative Pressure Wound Therapy (NPWT) is a new wound healing technology, and the negative pressure suction device is widely used in clinical wound healing treatment. The vacuum pump is the main working component as the negative pressure source. Aiming at the unstable negative pressure intensity caused by external interference, sensor delay and inaccurate modeling, a con-tinuous negative pressure control optimization method applied to the vacuum pump is proposed. Firstly, the key parameters of vacuum pump and catheter were extracted, and the mathematical model of vacuum suction device in wound treatment was established; secondly, combining BP neu-ral network and PID control, the dynamic control parameters of vacuum pump servo are identified and optimized, and fed back to the controller input; finally, a hybrid algorithm of Grey Wolf Optimi-zation (GWO) and Particle Swarm Optimization (PSO) is introduced to optimize the BP neural net-work to further improve the accuracy of the neural network. Through simulation, compared with the traditional PID, BP-PID and PSO-BP-PID, the proposed hybrid algorithm is advanced by 1.0s, 0.5s and 0.4s respectively, the steady-state error is reduced by 98%, 90% and 80% respectively, and there is almost no oscillation and overshoot. The experimental results show that the proposed hybrid algorithm has a good control effect on the negative pressure suction.

1. 引言

负压伤口治疗技术(NPWT)在促进各种创面修复中作用十分显著 [1] [2] [3]。负压吸引器结构模型如图1(a)所示，应用NPWT原理，在患者开放性创口处营造一个封闭的负压环境，在负压的作用下吸引去除渗出物，从而改善微血管血流，促进伤口愈合，可以有效防止感染的发生，进而帮助组织快速生长 [4] [5]。其操作机理如图1(b)所示。

负压吸引器在创面处产生的压力是影响创面治疗效果的关键，而真空泵作为负压吸引器的重要组成部分，其稳定运行至关重要。由于容积变化、传感器信号的延迟以及建模不精确等因素的影响，负压吸引过程存在着一定的干扰和不确定性。自PID算法提出以来，它在自动控制技术中占据了非常重要的地位。传统PID通过提前离线调节设置参数，在面对复杂的实际控制对象时，依靠传统的人工整定方法会导致速度慢和不准确的问题 [6]。

负压吸引器在创面处产生的压力是影响创面治疗效果的关键，而真空泵作为负压吸引器的重要组成部分，其稳定运行至关重要。由于容积变化、传感器信号的延迟以及建模不精确等因素的影响，负压吸引过程存在着一定的干扰和不确定性。自PID算法提出以来，它在自动控制技术中占据了非常重要的地位。传统PID通过提前离线调节设置参数，在面对复杂的实际控制对象时，依靠传统的人工整定方法会导致速度慢和不准确的问题 [6]。BP神经网络具有自适应、自组织以及自学习的特点，对工业过程控制中的流量、温度、压力以及成分等预测以及其他控制领域内都有着广泛的应用 [7] [8] [9]。将BP神经网路应用于控制算法中，优化PID的控制参数，通过自适应学习可以有效的克服系统参数变化和外部干扰的影响 [10]。郭清 [11] 等通过采用BP神经网络在线动态调整输出PID各参数的最优值，有效的缩短了系统的阶跃响应周期，且提高了控制精度。但是由于BP神经网络采用梯度下降法，初始值是随机选取的，这就使得BP神经网络在学习过程中容易陷入局部极值，从而导致网络出现振荡，影响整个系统的高效运行 [12]。

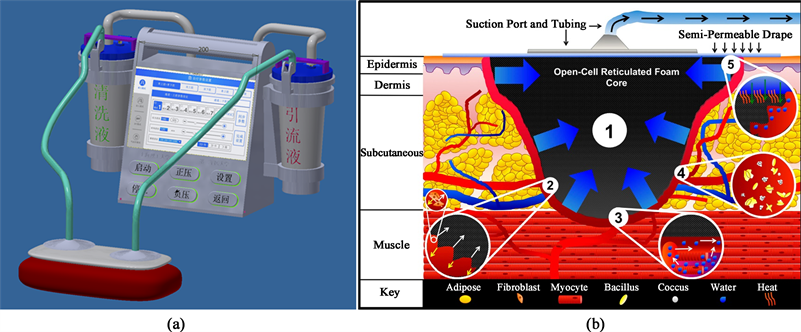
Figure 1. Operating mechanism of negative pressure wound treatment device. (a) Structure model of negative pressure suction device; (b) working mechanism of NPWT [5]

图1. 负压伤口治疗装置操作机理。(a) 负压吸引器结构模型；(b) NPWT工作机理 [5]

负压吸引器在创面处产生的压力是影响创面治疗效果的关键，而真空泵作为负压吸引器的重要组成部分，其稳定运行至关重要。由于容积变化、传感器信号的延迟以及建模不精确等因素的影响，负压吸引过程存在着一定的干扰和不确定性。自PID算法提出以来，它在自动控制技术中占据了非常重要的地位。传统PID通过提前离线调节设置参数，在面对复杂的实际控制对象时，依靠传统的人工整定方法会导致速度慢和不准确的问题 [6]。BP神经网络具有自适应、自组织以及自学习的特点，对工业过程控制中的流量、温度、压力以及成分等预测以及其他控制领域内都有着广泛的应用 [7] [8] [9]。将BP神经网路应用于控制算法中，优化PID的控制参数，通过自适应学习可以有效的克服系统参数变化和外部干扰的影响 [10]。郭清 [11] 等通过采用BP神经网络在线动态调整输出PID各参数的最优值，有效的缩短了系统的阶跃响应周期，且提高了控制精度。但是由于BP神经网络采用梯度下降法，初始值是随机选取的，这就使得BP神经网络在学习过程中容易陷入局部极值，从而导致网络出现振荡，影响整个系统的高效运行 [12]。

为了进一步提高控制效果，保证控制精度，需要对神经网络中的初始值进行优化选取。群体智能算法是一种智能优化算法，算法的机制大多是从生物或社会的行为中提取出来的 [13]，比如遗传算法(GA)、蚁群算法(AOC)等等。由于这些算法具有更好的寻找全局最优解的能力，因此被广泛应用于科学技术、工业等领域 [14]。灰狼算法是由Mirjalili等于2014年提出 [15]，模拟了自然界灰狼种群的领导层级和狩猎制度，具有设置参数少和寻优能力强的优点，预测准确度较高。但是灰狼算法局部收敛速度较慢，因此容易陷入局部最优解，通过引入非线性因子加快其收敛可以促使其跳出局部最优解。粒子群算法是通过模拟鸟群觅食行为而发展起来的一种参数简单、功能强大的群智能算法，自1995年提出粒子群算法以来，它已成功应用于科学和工程领域，如PID的调谐，路径估计，参数优化和机器人等领域，PSO算法结构简单，易于实现，特别是在求解非线性和不可微分的复杂优化问题时 [16]。因此，本文欲通过将粒子群算法与灰狼算法进行结合，在提高算法寻优的准确性的同时又可以更快速的收敛。

综上所述，本文针对负压引流器的控制效果不理想问题，通过真空泵系统及负压动力系统参数建立了其数学模型，提出使用BP-PID对负压吸引清创过程进行动态控制，为了进一步提高控制效果和控制精度，通过将GWO和PSO结合的混合算法，对神经网络的初值进行选取优化，最后通过实验证明了提出的控制方法的有效性。

2. 负压吸引器数学模型

负压吸引器主要包括一个产生吸力的泵，一个连接到半透水敷料上的吸口，以及对局部创面施加负压并将渗出液输送到收集单元的管道(腔管)。管腔、阀门和罐构成气动回路。负压吸引器工作原理图如图2所示。

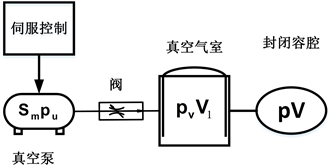
Figure 2. Working principle diagram of negative pressure suction device

图2. 负压吸引器工作原理图

负压吸引器在工作时，敷料贴于病人伤口处并在其上覆盖密封膜，在伤口处形成了一个微型的封闭容腔，其大小取决于伤口面积及伤口深度。通过负压泵持续抽取引流瓶内气体形成真空气室，病人伤口处的脓液等混合物也在负压的作用下不断的流入引流瓶内。

根据图2，由连续性方程、伯努利方程及真空技术基本方程等 [17] 对系统的负压回路进行分析，可得：

$V\frac{\text{d}p}{\text{d}t}=-S_{e}p+Q_1$ (1)

$S_e=SC/\left(S+C\right)$ (2)

$S=S_m\left(1-p_u/p\right)$ (3)

$\frac{1}{C}={{\displaystyle \sum }}^{\text{}}\frac{1}{C_i}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}$ (4)

其中p、V、S_e、Q₁分别为封闭容腔的压力、体积、入口抽速、泄漏量，S、S_m和p_u分别为真空泵实际抽速、名义抽速和极限压力；C₁、C₂、C₃分别为真空气室、电–气伺服阀及负压回路管路处的流导，C表示负压回路的总流导。

根据公式(1)~(4)，封闭容腔的压力p与负压回路总流导C有关，而C₁与C₃要远大于C₂，故封闭容腔的压力主要由电气伺服控制阀处的流导影响。阀口处的流量Q_m表示为

$Q_m=\{\begin{array}{l}C{p}_2{\rho }_0\sqrt{T_0/T_1}\sqrt{1-{\left(\frac{P_1/P_2-b}{1-b}\right)}^2},\left(p_1/p_2>b\right)\\ C{p}_2{\rho }_0\sqrt{T_0/T_1},\left(p_1/p_2\le b\right)\end{array}$ (5)

式中， ${\rho }_0$ 和T₀分别为标准大气压下的空气密度气体温度；T₁为当前温度；b为临界压力比，取0.3；p₁和p₂分别为阀口两端的压力

在考虑电–气伺服阀的流量后，得到负压回路的数学模型如下

$\frac{\text{d}p}{\text{d}t}=\{\begin{array}{l}-\frac{KR{T}_1{C}_{2}p{\rho }_0}{V}\sqrt{T_0/T_1}\\ \sqrt{1-\left(\frac{p_v/p-b}{1-b}\right)}\left(p_1/p_2>b\right)\\ -\frac{KR{T}_1{C}_{2}p{\rho }_0}{V}\sqrt{T_0/T_1}\left(p_1/p_2\le b\right)\end{array}$ (6)

$\frac{\text{d}{p}_v}{\text{d}t}=\frac{\text{d}p}{\text{d}t}-\frac{K{S}_m{p}_v}{v}\left(1-p_v/p\right)$ (7)

式中，v为泵到阀之间的管路体积；p_v为管路中的气体压力；K为绝热指数；R为气体常数。

根据建立的负压连续控制系统的数学模型，通过四阶龙格库塔方法进行求解，并采用Matlab控制软件进行仿真研究。系统采用将BP神经网络与PID控制相结合组成的BP-PID控制器进行控制。

3. BP神经网络PID控制算法

基于真空泵的负压连续控制系统，通过调节伺服控制装置，输出连续的负压信号，可以实现封闭容腔内负压高精度高响应连续可调。由于PID控制器具有简单、坚固、适应性强、可靠性高等优良性能，广泛应用于工业过程控制领域。PID控制器的控制算法分为增量式和位置式两种。经典增量式数字PID的算法公式为

$u\left(k\right)=u\left(k-1\right)+K_p\left[e\left(k\right)-e\left(k-1\right)\right]+K_{i}e\left(k\right)+K_d\left[e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right)\right]$ (8)

其中， $K_p$ 、 $K_i$ 和 $K_d$ 分别是PID控制器的比例增益、积分增益和微分增益。 $e\left(k\right)$ 是当前采样时间的预期输出与实际输出之间的差额，是当前采样时间的控制输出。

BP神经网络为三层前馈网络结构，由输入层、隐含层以及输出层组成，它使用梯度搜索技术来最小化预期输出值和实际输出值的均方误差，本文中的网络输入层有4个单元，隐藏层有5个单元，输出层有3个单元。BP神经网络的结构图如图3所示。

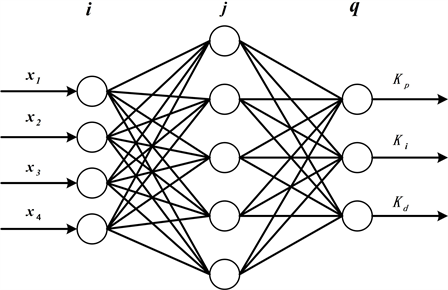
Figure 3. The structure of BP Neural Network

图3. BP神经网络的结构

根据式(8)设置神经网络的输入层为 $e\left(k\right)$ 、 $e\left(k\right)-e\left(k-1\right)$ 、 $e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right)$ 和常数1。即：

$\begin{array}{l}I{n}_1=x_1=e,I{n}_2=x_2=e\left(k\right)-e\left(k-1\right),\\ I{n}_3=x_3=e\left(k\right)-2e\left(k-1\right)+e\left(k-2\right),I{n}_4=x_4=1\end{array}$ (9)

隐含层采用Sigmoid作为激励函数，隐含层的输入、输出为：

$I_j\left(k\right)={\displaystyle \underset{j=0}{\overset{4}{\sum }}{\omega }_{ij}{x}_i}$ (10)

$O_j\left(k\right)=f\left(I_j\left(k\right)\right),\left(j=1,2,\cdots ,5\right)$ (11)

其中 ${\omega }_{ij}$ 为隐含层的加权系数，隐含层采用Sigmoid作为激励函数：

$f\left(x\right)=\text{tanh}\left(x\right)=\frac{{\text{e}}^x-{\text{e}}^{-x}}{{\text{e}}^x+{\text{e}}^{-x}}$ (12)

输出层的输入、输出为：

$I_q\left(k\right)={\displaystyle \underset{t=0}{\overset{4}{\sum }}{\omega }_{jq}{O}_j}$ (13)

$O_q\left(k\right)=g\left(I_q\left(k\right)\right),\left(q=1,2,3\right)$ (14)

其中 ${\omega }_{jq}$ 为输出层的加权系数，输出层使用非负的Sigmoid函数作为输出层神经元的激励函数：

$g\left(x\right)=\frac{1}{2}\left(1+\tanh \left(x\right)\right)=\frac{{\text{e}}^x}{{\text{e}}^x+{\text{e}}^{-x}}$ (15)

输出层的三个输出分别对应的是BP神经网络PID控制器的参数 $K_p$ 、 $K_i$ 和 $K_d$，分别如下：

$O_q\left(1\right)=K_p,O_q\left(2\right)=K_i,O_q\left(3\right)=K_d$ (16)

性能指标输出误差二次方函数 $E\left(k\right)$ 如下：

$E\left(k\right)={\left(r_{in}\left(k\right)-y_{out}\left(k\right)\right)}^2/2$ (17)

通过应用梯度下降法对神经网络的权值系数进行在线动态修正，可得权值系数变换公式为：

$\Delta {\omega }_{ij}\left(k\right)=\eta {\delta }_q{O}_J\left(k\right)+\alpha \Delta {\omega }_{ij}\left(k-1\right)$ (18)

${\delta }_q=e\left(k\right)\mathrm{sgn}\left(\frac{\partial y\left(k\right)}{\partial u\left(k\right)}\right)\frac{\partial u\left(k\right)}{\partial O_q\left(k\right)}{g}^{\prime }\left[I_q\left(k\right)\right]$ (19)

其中 $\eta$ 为学习速率， $\alpha$ 为惯性因子，而隐含层的权值计算公式同理：

$\Delta {\omega }_{jq}\left(k\right)=\eta {\delta }_{j}I{n}_i\left(k\right)+\alpha \Delta {\omega }_{jq}\left(k-1\right)$ (20)

${\delta }_j=f^{\prime }\left[I_j\left(k\right)\right]{\displaystyle \underset{q=0}{\overset{2}{\sum }}{\delta }_q{\omega }_{jq}\left(k\right)}$ (21)

式中

$g^{\prime }\left[x\right]=g\left(x\right)\left[1-g\left(x\right)\right],f^{\prime }\left[x\right]=\frac{1-f^2\left(x\right)}{2}$ (22)

BP神经网络采用梯度下降法，迭代过程中的学习率 $\eta$ 和惯性系数 $\alpha$ 的初值对结果影响较大，若初值设置不合理可能会在迭代过程中陷入局部极值，从而导致网络出现振荡，影响控制的性能。因此，需对初值的设置进一步优化。

4. 混合算法优化BP-PID控制算法

为了保证控制精度，提高控制效率，BP神经网络的初值的选取至关重要，本文欲采用GWO结合PSO算法在迭代中对 $\eta$ 和 $\alpha$ 进行全局寻优，从而保证BP神经网络能够更为精准有效的找到动态控制参数，提高控制系统的稳定性。应用GWO-PSO混合算法优化BP-PID控制系统的结构如图4所示。

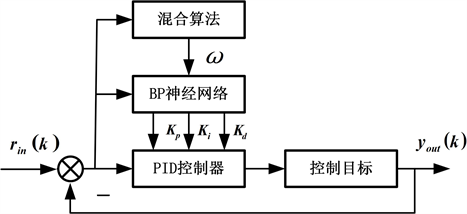
Figure 4. Structure of BP-PID control system optimized by hybrid algorithm

图4. 混合算法优化BP-PID 控制系统结构图

总体的适应度函数由BP网络的输出与预期输出值之间的方差函数表示，并根据 [18] 有

$F=\frac{1}{T}\underset{i=1}{\overset{T}{{\displaystyle \sum }}}{\left(y_i-{y^{\prime }}_i\right)}^2$ (23)

式中，T为训练次数； $y_i$ 与 ${y^{\prime }}_i$ 分别为第i次的预测输出和期望输出。

灰狼算法源于自然界中灰狼的等级制度与狩猎行为，根据计算得到的适应度值将整个狼群分为最优、次优、第三优灰狼和其他灰狼四个等级，并分别简称 $\alpha$ 狼， $\beta$ 狼、 $\delta$ 狼和 $\omega$ 狼。通过计算灰狼个体与猎物之间的距离，实现灰狼位置的更新。

灰狼 $\omega$ 的位置更新如下

$X\left(t+1\right)=\frac{A_1{X}_1+A_2{X}_2+A_3{X}_3}{C_1+C_2+C_3}$ (24)

其中，X₁，X₂，X₃是 $\alpha$ 狼， $\beta$ 狼和 $\delta$ 狼的位置，系数A₁，A₂，A₃，C₁，C₂，C₃根据下式计算所得：

$A=2a\cdot r_1-a$ (25)

$C=2r_2$ (26)

其中，r₁和r₂是0到1之间的随机数，a是收敛因子，计算式如下：

$a=2-2\left(\frac{1}{e-1}\times \left(e^{\frac{t}{m}}-1\right)\right)$ (27)

直到迭代结束，选取最优的 $\alpha$ 狼作为输出，表示为

$x_{gwo}=\left[\eta ,\alpha \right]$ (28)

由PSO进行下一步的迭代，并记为

$x_{i,j}={\left[\eta ,\alpha \right]}_{ij}$ (29)

根据灰狼算法产生的输出随机选择PSO的第一个粒子，如下式：

$x_{1,j}=rand\left(\left[x_{gwo}-\tau ,x_{gwo}+\tau \right]\right)$ (30)

其中， $\tau$ 为参数公差。粒子的下一次迭代如下

$x_{i,j}=x_{i-1,j}+v_{i,j}$ (31)

其中 $v_{i,j}$ 表示粒子的迭代速度和方向，表示如下：

$v_{i,j}={\lambda }_i\times v_{i-1,j}+c_1\times ran{d}_1\times p_{best,i-1}-c_2\times ran{d}_2\times g_{best}-x_{i,j}$ (31)

其中 $ran{d}_1$ 和 $ran{d}_2$ 是介于0~1之间变化的随机数； $c_1$ 和 $c_2$ 为加速常数， $p_{best,i-1}$ 和 $g_{best}$ 分别为粒子最优位置和全局最优位置。 ${\lambda }_i$ 为惯性权重，由下式计算：

${\lambda }_i=0.05\times {\lambda }_{i-1}$ (32)

基于混合算法的设计流程图如图5所示。

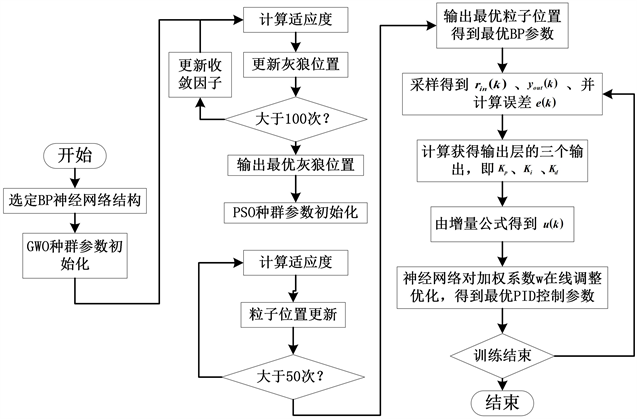
Figure 5. Optimization of BP-PID control algorithm flow based on hybrid algorithm

图5. 基于混合算法优化BP-PID 控制算法流程

5. 实验与分析

5.1. 算法仿真分析

首先应用Matlab进行仿真，本文中混合算法的最大迭代设置为150次，其中100次由GWO完成，其余的通过PSO继续进行迭代。GWO和PSO的种群规模均为30。图6表示混合算法每次迭代中最佳目标函数的值。

由图6可知，目标函数在前100次迭代中迅速收敛，这表明通过GWO确定的最佳目标函数值逐渐向全局最优收敛，但最后趋于平稳且收敛缓慢，而后在迭代的后1/3部分进一步收敛至最优解，这表明通应用PSO算法有效的提高了算法的收敛速度。

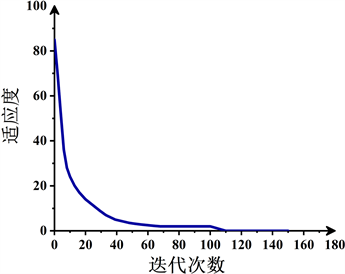
Figure 6. Curve of fitness function change

图6. 适应度变化曲线图

为了验证本文提出的复合算法优化BP-PID控制器的控制效果，通过提前设置BP神经网络的学习因子α为0.05，惯性系数η为0.5，并根据传统PID参数设置的实际经验提前设置比例积分微分控制系数。控制系统网络结构和初始参数如表1所示。

Table 1. Network structure and initial parameters

表1. 网络结构及初始参数

首先记录下控制器的阶跃响应曲线，并分析同等条件下应用混合算法优化的控制效果同传统PID、BP-PID、和PSO-BP-PID进行对比，得到阶跃响应曲线图、误差曲线图对比图如图7，图8所示。

由图7和图8可以看出，传统的PID控制波动较大，超调明显且趋于平稳用时最长。应用BP-PID进行控制，虽然有效避免了振荡，但还是存在一定的超调，且趋于稳态用时依旧较长。引入了PSO算法的PSO-BP-PID控制相较于传统PID和BP-PID控制有效的减少了趋于稳态的用时，但仍存在一定的超调现象，说明单独应用PSO算法的寻优效果并不理想。而采用GWO和PSO的混合算法下的BP-PID控制的控制效果表现相对良好，不仅在很短的时间内就收敛至目标，且超调更小，验证了混合算法优化下控制的有效性。

将四种控制方法仿真得到的阶跃响应结果数据进行处理得到关于稳态时间、稳态误差、振荡次数和最大超调量四个指标数值，如表2所示。

从表2可以看出，本文提出的GWO-PSO-BP-PID稳态用时0.2 s相较于其他三种控制器分别提前了1.0 s、0.5 s和0.4 s，稳态误差分别减少了98%、90%和80%，且几乎无超调和振荡现象，说明应用GWO-PSO-BP-PID算法下的控制器有效的提高了系统的响应速度、控制精度以及系统的稳定性。

Figure 7. Step response curve

图7. 阶跃响应曲线图

Figure 8. Error curve

图8. 误差变化曲线图

Table 2. Comparison of performance indexes

表2. 性能指标对比

5.2. 实验与应用

实验装置图如图9所示，主要工作元件包括引流瓶、过滤器、压力传感器、压力阀、真空泵、树莓派、电源驱动模块、敷料及导管等组成。

Figure 9. Schematic diagram of experiment

图9. 实验示意图

基本结构参数如表3所示。其中真空泵选用型号为KPV8。

Table 3. Structural parameters

表3. 结构参数

将控制器用于负压吸引控制系统中，根据文献 [17] 得知，负压吸引治疗过程中的最佳负压值为−125~−450 mmHg (−0.017~−0.060 MPa)，通过提前设定期望压强为−0.04 Mpa，在室内温度为15的情况下采用XGZP040DB1R系列的压力传感器，并记录压力随时间变化的数据，得到负压变化曲线如图10所示。

从图10中可以看出，开始时压力并没有变化，这是由于此时真空室气体持续抽取中，压力变化不太明显，而曲线在4秒开始压力值迅速变化，在10s时收敛到接近40 kpa并趋于稳定，且几乎没有产生超调，在初始设定目标压力值为33.9 kpa的情况下，其稳态误差较小，表明该控制器对于负压吸引器有良好的控制效果。

6. 结论

本文以负压引流器为研究对象，针对在控制过程中存在外部干扰、传感器延迟以及建模不精确等引起的负压强度不稳定的现象，首先建立了负压引流器工作过程中的数学模型，然后采用BP神经网络和PID控制算法结合，通过识别并优化真空泵伺服动态控制参数，并反馈到控制器输入端。最后引入灰狼算法和粒子群算法的混合算法优化BP神经网络，进一步提高了控制精度和控制效果。通过仿真实验，应用GWO-PSO-BP-PID控制器的阶跃响应只需要0.2 s，比较于传统PID、BP-PID和PSO-BP-PID三种

Figure 10. Pressure change curve

图10. 压力变化曲线

控制器分别提前了1.0 s、0.5 s和0.4 s，稳态误差分别减少了98%、90%和80%，振荡次数和最大超调量为0，相较于BP-PID和PSO-BP-PID控制器振荡次数2次，几乎实现了无振荡和超调，稳态误差仅为0.0001。说明GWO-PSO-BP-PID控制器具有良好的控制性能。另外，通过实验验证在预设目标为33.9 kpa下，在几乎没有超调的情况下实现了稳定控制，验证了该控制方法对负压吸引器动态控制的有效性，为研究负压吸引器的动态控制以及相应控制算法的优化提供了一种新的思路，具有一定的现实意义。

基金项目

国家自然科学基金(No.51375314)资助项目。

NOTES

^*通讯作者。