织物射流冲击干燥下温度变化数值模拟

Numerical Simulation of Temperature Change of Fabric under Jet Impingement Drying

摘要: 本文针对织物射流冲击干燥特性建模中对流换热系数与主流温度设定困难的问题，采用UDF程序对ANSYS FLUENT进行二次开发，耦合了射流冲击外流场供热与织物内水分蒸发过程，建立了射流冲击下织物干燥特性模型，探索了热风速度、热风温度、织物密度、织物厚度等参数对冲击干燥下织物温度的影响，研究了5种不同织物干燥过程的温度变化曲线差异，并开展相关实验验证。结果表明：针对不同织物材料参数，织物克重对织物干燥特性影响最大，比热容影响最小，孔隙率和材料密度的影响类似；对不同种类织物，棉织物表观密度最大，所需干燥时间最长约56 s，聚脂纤维表观密度最小，所需干燥时间为最短约33 s；该研究可为印染热定型设备设计与生产工艺参数优化提供理论参考，具有较好的社会效益与经济效益。

Abstract: In order to solve the problem that it is difficult to set the convective heat transfer coefficient and the mainstream temperature in the modeling of the jet impact drying characteristics of porous fabrics, the software ANSYS FLUENT was secondary developed by using the UDF program. The external sup-ply of heat and the water evaporation process in the porous fabric under the jet impact were cou-pled, and the drying characteristics model of the fabric under the jet impact without convective heat transfer coefficient was established. The effect of hot wind velocity, hot wind temperature, fab-ric density, fabric thickness and other parameters on the temperature of the porous fabric under impact drying was explored. The differences in the temperature variation curves of five different fabrics during the drying process were studied. And build related experiments to verify the simula-tion model. The results show that: for different fabric material parameters, the fabric weight has the greatest influence on the drying characteristics of the fabric, and the specific heat capacity has the least influence. The influence of porosity and material density is similar. For different types of fab-rics, cotton fabric has the highest apparent density and the longest drying time is about 56 s, while polyester fiber has the lowest apparent density and the shortest drying time is about 33 s. This study can provide theoretical reference for the design of printing and dyeing heat setting equip-ment and the optimization of process parameters, and has good social and economic benefits.

1. 引言

当前，控制碳排放已成为国际社会的共识 [1]。作为高排放、高能耗的印染行业，亟需加快设备升级，进一步降低印染热定型设备能耗。在印染行业中，热风干燥被广泛使用 [2] [3]。目前，在热定形设备制造上我国已具备较强的能力，但与国际先进水平相比在能耗、高端织物热定形性能等方面仍有较大的差距 [4] [5]。因此，有必要开展织物干燥过程传热传质机理研究，为印染热定形装备的结构设计和热定形工艺参数优化提供理论依据 [6]。

国内外研究者已对织物干燥过程的水分传热传质特性开展了相关的研究。Etemoglu等 [7] 建立了热风冲击下织物传热传质模型，研究了热风温度、热风速度等工艺参数对织物干燥特性的影响。Akyol等 [8] 采用神经网络算法对织物的干燥特性进行了建模，预测了织物的干燥过程，得到了较佳的温度、压力等工艺参数。Khan等 [9] 研究了湿度和热风速度对多孔介质干燥的影响规律，利用非热平衡传热传质理论建立了其干燥特性模型，并通过实验对计算模型进行了验证。Elhalwagy等 [10] 运用计算流体动力学(CFD)建立了多孔材料的干燥特性模型，发现多孔材料干燥阻力与材料自身特性直接相关。Defraeye等 [11] [12] 利用FLUENT软件和自编写HAM程序，对多孔介质干燥过程的气体流动区域和干燥特性进行了分析，与利用热平衡的计算结果进行了对比分析，对传热传质类比关系进行了验证。钱淼等 [13] [14] [15] 研究了织物在冲击干燥下的传热传质特性，建立了二维织物干燥传热传质模型，对织物的温度变化进行了预测。热风冲击干燥多孔织物时，主要通过对流向织物传递热量。上述的常用干燥模型中的对流换热系数往往设定为恒定值。可是热空气冲击干燥过程中对流换热系数会随时间发生变化，这使得前期已建立的基于集总参数法干燥特性模型在分析冲击干燥织物传热传质过程存在一定的不足 [16]。

本文通过UDF (User Defined Function)和FLUENT联合仿真，耦合了热空气流场和织物内水分蒸发的织物热风冲击干燥过程 [17]。通过编写UDF将织物干燥数学模型添加到FLUENT中，首先通过FLUENT计算出热流密度q，在通过UDF计算得到织物干燥过程的温度/水分变化情况。通过联合仿真，FLUENT自动得到热风传递给织物的瞬时热流密度，无需输入对流换热系数和主流温度，避免了随时间变化对流换热系数确定困难的问题。基于该模型，本文研究了热风速度、温度等外部物理特性和织物密度、厚度、初始含水率等织物自身特性对冲击干燥过程的温度变化的影响，并对棉、丝绸、羊毛、聚酰胺纤维、聚脂纤维织物的干燥特性进行了研究。本文的研究结果可为纺织印染热定型过程中的装备设计与工艺参数优化提供一定的参考价值。

2. 多孔织物热风冲击干燥建模

首先对多孔织物热风冲击干燥物理问题进行合理简化，将其简化为二维圆周对称的物理模型，然后分别对外流场和多孔织物进行建模，最后通过FLUENT二次开发将外流场和多孔织物的数值模型耦合，用于计算得到多孔织物热风冲击干燥整体的温度变化分布。

2.1. 物理模型建立

织物在进行热定形干燥时，由风道喷嘴吹出的热风直接冲击在织物上，单个喷嘴在织物上的冲击作用区域为一圆形区域。为减少计算量，在本文中将实际冲击干燥的三维流场简化为只有长L和高H的二维圆周对称的物理模型，忽略织物厚度影响，利用冲击作用区域圆周对称特性，将织物的计算区域简化为一条直线 [18] [19]。

2.2. 射流冲击外流场建模

图1所示为简化后的织物计算域示意图，其中将单喷嘴织物冲击干燥的外流场简化为长27 mm、高150 mm的二维计算区域。外流场假设如下：热风工质为空气；热风流动状态为湍流；由于热风温度变化不大，因此热风物性参数设置为常数。边界条件设定如下：喷嘴出口为速度进口，冲击表面(织物表面)设置为壁面，将每个壁面设为绝热边界条件。

本文采用计算流体动力学软件FLUENT对外流场进行数值模拟。在求解过程中，连续性、动量、能量和湍流方程采用SIMPLE算法求解。

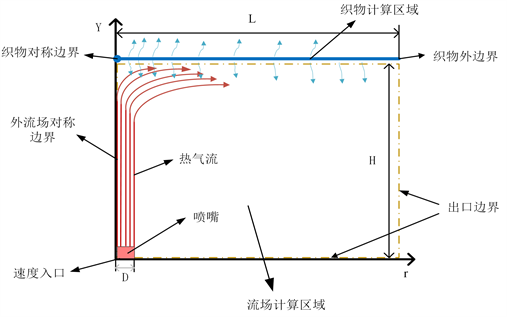
Figure 1. Simplified diagram of fabric calculation area

图1. 织物计算区域简化示意图

2.3. 多孔织物干燥建模

织物内部水分蒸发模型采用集总参数模型。由于简化的织物模型计算域为圆对称，因此将多孔织物在干燥过程中的控制方程建立在极坐标下。

能量守恒方程 [20] [21] [22]：

$\rho c_{\text{p}}\times H\times \frac{\partial T}{\partial \tau }=q-h_{\text{a}}\left(T-T_{\text{a,e}}\right)+\frac{1}{r}\times \frac{\partial }{\partial r}\left(\frac{\partial T}{\partial r}\times r\times k\right)\times H-m_{\text{s}}\times \alpha$ (1)

式中，ρc_p项可用式(2)表示：

$\rho c_{\text{p}}={\rho }_{\text{ros}}\times c_{\text{ros}}+{\rho }_{\text{ros}}\times c_{\text{L}}\times U$ (2)

其中：ρ为多孔织物的绝干密度，kg/m³；c_p为多孔织物的的比热容，J/(kg∙K)；H为织物厚度，m；T为织物温度，K；τ为干燥时间，s；h_a为自然对流换热系数，W/(m²∙K)；T_a,e为环境温度，K；k为多孔织物的导热系数，W/(m∙K)；α为水的汽化潜热，J/kg；ρ_ros为多孔织物的固相纤维密度，kg/m³；c_ros为多孔织物固相纤维比热容，J/(kg∙K)；c_L为水的比热容，J/(kg∙K)；U为干基含水率，%；m_s为织物蒸发速率，kg/(m²∙s)。织物蒸发速率可用式(3)表示：

$m_{\text{s}}=h_{\text{m}}\left({\rho }_{\text{v}}-{\rho }_{\text{ve}}\right)$ (3)

其中：h_m为织物表面传质系数，m/s；ρ_v为水蒸气密度，kg/m³；水蒸气密度可用式(5)表示：

${\rho }_{\text{v}}=\frac{P\times M}{R\times T}$ (4)

质量守恒方程：

${\rho }_{\text{ros}}\times H\times \frac{\partial U}{\partial \tau }={\rho }_{\text{ros}}\times H\times \frac{1}{r}\times \frac{\partial }{\partial r}\left(\frac{\partial U}{\partial r}\times r\times D_L\right)-m_{\text{s}}$ (5)

其中，水分在织物中的扩散系数D_L可用式(6)表示 [23]：

$D_{\text{L}}=D_{\text{0}}\left(\frac{U_{\text{0}}-U_{\text{eq}}}{U_{\text{ms}}-U_{\text{eq}}}\right)\times {\text{e}}^{-\frac{E_{\text{d}}}{RT}}$ (6)

在r = 0处设置为对称边界条件；在r = L处，设置为与外界无热量和水分传递的边界条件，数学方程可用式(7)~(8)表示：

$\frac{\partial T}{\partial r}=0$，r = 0或r = L (7)

$\frac{\partial U}{\partial r}=0$，r = 0或r = L(8)

本文使用有限差分法求解上述多孔织物干燥数学模型，将上述微分方程改写为差分方程，表达式如下：

$\begin{array}{c}\rho c_{\text{p}}{}_i^{n-1}\times H\times \frac{T_i^n-T_i^{n-1}}{\Delta \tau }=h_{\text{c}}\times \left(T_{\text{hot}}-T_i^n\right)-h_{\text{a}}\times \left(T_i^n-T_{\text{a,e}}\right)-m_{\text{s}}{}_i^n\times \Delta h_w\\ +\frac{k_i^n{r}_i{T}_{i+1}^n-\left(k_i^n{r}_i+k_{i-1}^n{r}_{i-1}\right)T_i^n+k_{i-1}^n{r}_{i-1}{T}_{i-1}^n}{\Delta r^2}\times H\times \frac{1}{r_i}\end{array}$ (9)

${\rho }_{\text{d}}\times H\times \frac{U_i^n-U_i^{n-1}}{\Delta \tau }=\frac{D_{\text{L}}{}_i^n{r}_i{U}_{i+1}^n}{\Delta r^2}+\frac{D_{\text{L}}{}_{i-1}^n{r}_{i-1}{U}_{i-1}^n}{\Delta r^2}\times {\rho }_{\text{d}}\times H\times \frac{1}{r_i}-m_{\text{s}}{}_i^n-\frac{\left(D_{\text{L}}{}_i^n{r}_i+D_{\text{L}}{}_{i-1}^n{r}_{i-1}\right)U_i^n}{\Delta r^2}$ (10)

$\frac{U_i^n-U_i^{n-1}}{\Delta \tau }=0$，r = 0或r = L (11)

$\frac{T_i^n-T_i^{n-1}}{\Delta \tau }=0$，r = 0或r = L (12)

2.4. 外流场与织物干燥耦合方法与流程

图2所示为多孔织物冲击干燥过程的热风与织物界面的传热传质过程。热风射流与织物表面发生碰撞，在界面处通过对流换热干燥织物，并蒸发水分带走织物吸收热风带来的能量E [24]。

通过二次开发FLUENT，编写UDF将上述织物干燥数学模型添加到FLUENT计算中，实现外流场供热与织物内水分蒸发的耦合计算。外流场冲击下多孔织物干燥过程的计算流程如图3所示。由FLUENT软件仿真得到外流场与织物界面处的瞬时热流密度q的分布，并将界面单元的热流密度q和ID储存到UDM (User Defined Memory)中。UDF将UDM中的热流密度q匹配到多孔织物计算单元ID上，将其代入到多孔织物干燥数学模型中得到多孔织物的温度变化情况，计算完成后将结果保存到UDM中，为下一时间步长FLUENT流场计算提供数据。为提高计算效率、减少计算时间，FLUENT采用并行计算同时编写并行多核心UDF程序。

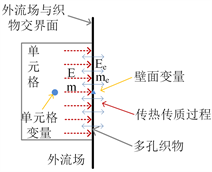
Figure 2. Fabric drying process under the impact of hot air flow

图2. 织物在热气流冲击下干燥过程

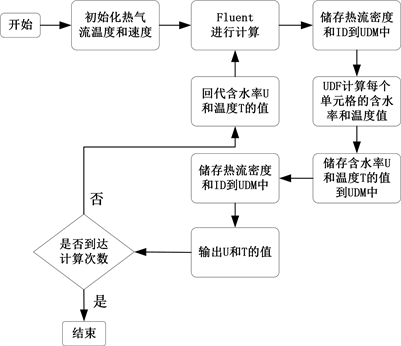
Figure 3. Drying mathematical model overall calculation flow chart

图3. 干燥数学模型整体计算流程图

3. 多孔织物热风冲击干燥实验

为验证计算模型的可行性，本文以棉织物为实验对象，开展相关实验研究。实验系统主要由干燥炉、轧车系统、热风机、红外热成像仪组成，实验系统如图4所示。具体实验过程如下：

Figure 4. Experimental system

图4. 实验系统

首先将织物放到恒温干燥箱至完全干燥，对织物进行多次称重，取平均值，并测量织物的尺寸，计算得到织物的体积平均密度。根据式(13)计算得到织物的孔隙率 [25]：

$\theta =\frac{V_{\text{d}}}{V_{\text{d}}+V_{\text{s}}}=\frac{\rho }{{\rho }_{\text{p}}}\times 100\%$ (13)

其中，V_d为织物的孔隙体积，m³；V_s为织物固体基材所占体积，m³；ρ_p为多孔织物的本征固体密度，kg/m³；ρ为多孔织物的体积平均密度，kg/m³。

对于织物干燥，含水率是影响织物干燥过程的一个重要初始条件，本文选用干基含水率来描述织物干燥过程中水分变化，实验中首先将干布放入水中静置一段时间，利用轧车对含湿织物进行湿度均匀化处理，并对处理后的湿织物进行称重处理，计算其干基含水率。干基含水率 [26] 可用式(14)表示：

$X=\frac{m_{\text{l}}}{m_{\text{l}}+m_{\text{d}}}\times 100\%$ (14)

其中，m_l为织物内液态水的质量，kg；m_d为干燥织物的质量，kg，可近似为织物干质固体的质量。

接下来调节好风机风速和温度，预运行风机20分钟，保证喷嘴出口风速和温度达到稳定。当温度仪测试的喷嘴出口温度稳定后，热风开始垂直吹向织物表面使其升温，红外摄像机开始记录织物的温度变化。热风温度和风速由温度仪和风速仪测量得到。每个实验进行三次，当织物的温度分布没有变化时，红外摄像仪停止记录。

4. 仿真结果与分析

首先对棉织物干燥特性在不同喷嘴热风速度和温度条件下进行模拟，将模拟结果和实验结果进行比较，验证数值模型的可靠性。然后对织物在不同的干燥条件进行模拟分析，得出不同织物材料参数对织物干燥特性的影响规律，最后，对织物材料参数在不同种类织物的影响规律做进一步的模拟分析，得出织物自身物理参数对织物干燥特性的影响差异。

4.1. 理论与实验对比

通过实验和模型计算，织物中心点温度随时间变化曲线如图5所示。在喷嘴出口V = 8.6m/s，T = 125℃，V = 4.6 m/s T = 125℃，V = 8.6 m/s，T = 110℃三种条件下，通过对模拟与实验的中心点温度随时间变化曲线进行对比发现：模型的计算结果与实验结果一致，最大误差小于5%，表明了理论模型的可行性。

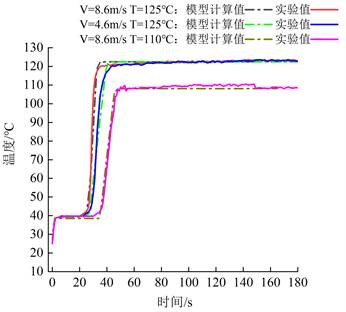
Figure 5. The time-dependent curve between the model calculated value and the experimental measured value of the central point temperature of the fabric drying process is obtained

图5. 织物干燥过程中心温度的模型计算值与实验测量值随时间变化曲线

通过对图5中干燥特性曲线的对比，可以发现：织物外部热气流的变化对织物干燥过程有显著的影响，提高热风出口的V和T，能够加快织物干燥过程，提高织物干燥完成后温度。当T = 125℃和V = 8.6 m/s时，织物从开始干燥到干燥完成所需时间t = 41 s，降低温度后T = 110℃时织物完成干燥t = 56 s，降低出口风速后V = 4.6 m/s织物完成干燥t = 46 s。通过对比发现T比V对织物干燥特性影响更大，降低T织物所需干燥时间t增加36%，而降低V织物干燥所需时间t增加12%。具体表现为，织物恒速干燥段时间缩减，降速干燥段和干燥完成段曲线斜率增大，干燥完成段织物最终平衡温度增加。在实际印染热定形工艺参数设定时，可在适当提高温度的同时增加风速，来提高织物干燥性能。

4.2. 不同干燥条件织物干燥特性曲线研究

本文研究织物比热容c_ros、材料密度ρ_ros、孔隙率θ、克重ω 4个材料参数对冲击干燥特性的影响规律，计算模型设置为T = 125℃，V = 8.6 m/s，改变干燥模型中相应的物理参数值，得到了不同参数下织物中心点温度随时间变化特性曲线，如图6(a)~(d)所示。由图中温度变化曲线的对比可见：比热容c_ros对织物干燥特性的影响较小，克重ω对织物干燥特性的影响最大，孔隙率θ和材料密度ρ_ros对织物干燥特性的影响较为接近。

由图6(a)还可见，c_ros分别为670 J/kg/K、1210 J/kg/K和1360 J/kg/K时，织物各个干燥阶段所需时间差距小于5%，并且各个干燥阶段的平衡温度差距同样小于5%。由于c_ros表示物质提高温度所需热量的能量，而不是吸收或者散热能力，热风冲击干燥过程提供的能量完全超过织物提高温度所需能量，从而导致c_ros对织物干燥特性的影响较小。图6(b)和图6(c)反映了θ和ρ_ros对干燥特性的影响，θ和ρ_ros两者的影响类似，这是由于θ和ρ_ros的改变会直接导致织物结构特性的改变，随着θ和ρ_ros的增大，热风穿透织物更加困难，织物背风侧传热传质能力下降导致降速干燥段和干燥完成段温度上升速度有所放缓，但恒速干燥段时间增加，织物干燥最终温度无变化。图6(d)反映了ω对织物干燥特性的影响，这里“克重”是指一平方米织物的重量克数。ω增加会直接导致织物含水率、密度、孔隙率等的增加，致使冲击热风对织物穿透能力和织物背风侧传热传质能力均下降，水分蒸发所需能量增加。当ω为75 g/m²时总用时32 s，当ω增加到200 g/m²时总用时76 s，总时间增加超过137%，由此可见织物ω增加会使织物干燥时间快速增加。但织物各个干燥阶段的平衡温度变化极小，织物ω对干燥的平衡温度影响不大。因此在设定热定型的工艺参数时，可对不同材料的织物进行对比分析，根据不同织物物理特性之间的差异，对已有的工艺进行一定的改进。

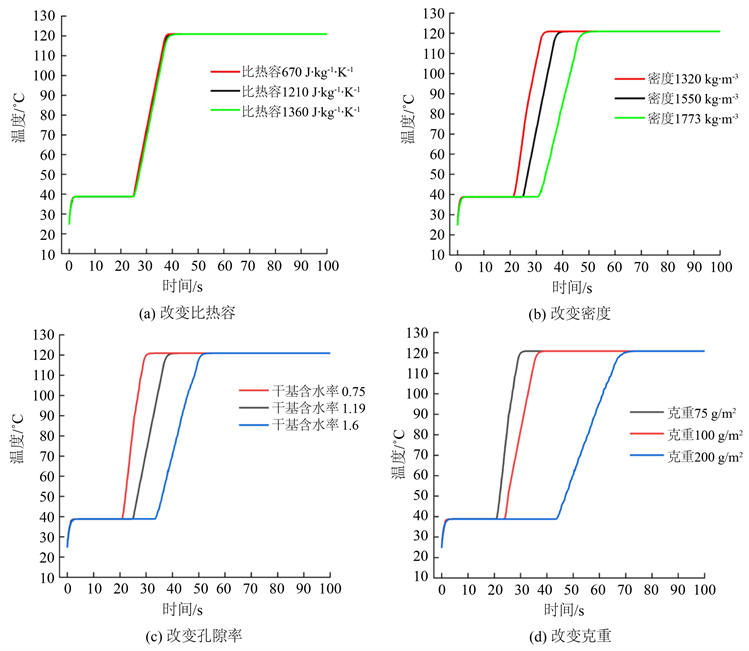
Figure 6. Change curve of fabric center temperature with time under different material parameters

图6. 不同材料参数下织物中心温度随时间变化曲线

4.3. 不同种类织物对比

为了研究不同种类织物在相同冲击干燥条件下的干燥特性，以5种厚度均为2 mm的常见纺织材料作为研究对象，其部分物理特性见表1所示 [27]。

Table 1. Physical properties of fabric

表1. 织物物理特性

其中织物的表观密度是指材料密度和孔隙率的乘积。通过UDF与FLUENT联合仿真得到不同种类织物对应的中心点温度随时间变化特性曲线，如图7所示。

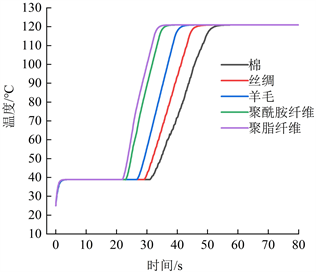
Figure 7. Change curve of center temperature of different kinds of fabric with time

图7. 不同种类织物中心温度随时间变化曲线

由图7可见：5种织物在干燥时间上各不相同，但在恒速干燥段和干燥完成后的温度相同，可见织物自身物理参数对2个平衡段的温度影响不大，改变织物种类主要会导致冲击干燥时间发生变化。在上文中发现c_ros对干燥特性影响较小，ω影响最大，增大θ和ρ_ros会明显增加干燥时间，其中θ和ρ_ros的乘积为表观密度ρ_θ。通过对5种织物参数的对比发现，棉织物ρ_θ最大，所需干燥时间也最长约56s，聚脂纤维ρ_θ最小，所需干燥时间为最短约33 s。另外聚脂纤维与聚酰胺纤维ρ_ros不同，θ也不同，但它们的乘积表观密度ρ_θ，较为接近，所需干燥时间也较为接近，这就解释了图中5种织物干燥特性曲线为何会各不相同。由此可以发现θ和ρ_ros的乘积表观密度ρ_θ可以为织物干燥特性提供一定的预判价值。

5. 结论

本文采用FLUENT软件并通过编写UDF程序对单喷嘴情况下织物的冲击干燥特性进行了分析研究，并通过实验对数学模型的可靠性进行了验证，得到以下主要结论：

1) 研究发现V、T、ρ_ros、θ、ω发生改变对织物冲击干燥特性产生较为明显的影响，c_ros发生改变对织物冲击干燥特性影响较小。增大T会提高织物最终干燥完成时的温度。增加ρ_ros、θ均会降低织物的干燥速率，延长干燥时间t，但不改变织物最终干燥完成时的温度。

2) 通过对棉、丝绸、羊毛、聚酰胺纤维、聚脂纤维5种不同织物干燥特性曲线的计算，得到了5种织物的干燥特性，结果表明5种织物在干燥时间上各不相同，但恒速干燥段和干燥完成后的温度相同。另外θ和ρ_ros的乘积表观密度ρ_θ，可以为织物干燥特性提供一定的预判价值。

本文基于ANSYS FLUENT，采用UDF程序对其进行二次开发，设计了考虑外流场传热及织物内传热传质的耦合织物单喷嘴冲击干燥特性算法，相较传统织物干燥模拟精确度进一步提高，可为印染热定形机设计和热定形工艺参数优化提供理论参考。

基金项目

浙江省重点研发计划(2023C01158)。