基于水凝胶的血管吻合器设计与实验研究

Design and Experimental Study of Vascular Stapler Based on Hydrogel

摘要: 研究基于水凝胶增强的椎动脉血管吻合器，并验证其可靠性。利用海藻酸钙水凝胶作为血管连接与防渗漏关键部件，分别设计了贴合式和袖套式水凝胶血管吻合器，运用ANSYS软件进行了流固耦合的有限元计算，最后进行了离体实验，对比分析两种吻合模型的血管的变形及壁面剪切应力分布、水凝胶的变形及应力应变分布和血管爆破压大小。在两种结构设计中血液流动均表现平稳，具有较好的吻合和粘合条件。其中袖套式吻合模型中水凝胶所受应力应变较小，分别为15.679 Pa，0.3%；爆破压测试中袖套式吻合血管所能承受的压力较正常血管相近，保持在1321.1 mmHg左右。研究表明，水凝胶材料在血管吻合器设计具有较好的潜在应用，对比不同结构设计，袖套式吻合方法较贴合式吻合方法更加可靠。

Abstract: To study the vertebral artery vascular stapler based on hydrogel enhancement and verify its relia-bility. Calcium alginate hydrogel was used as the key component of vascular connection and leakage prevention. The fitting type and sleeve type hydrogel vascular stapler were designed respectively. The finite element calculation of fluid-structure coupling was carried out by ANSYS software. Finally, the in vitro experiment was carried out. The blood vessel deformation and wall shear stress distri-bution, hydrogel deformation and stress-strain distribution and vessel bursting pressure were compared and analyzed. The blood flow was stable in both structures with good anastomosis and adhesion conditions. In the sleeve anastomosis model, the stress and strain of hydrogels were smaller (15.679 Pa, 0.3%). In the burst pressure test, the pressure of the sleeve anastomotic vessel was similar to that of the normal vessel, and kept at about 1321.1 mmHg. Studies have shown that hydrogel materials have a good potential application in vascular stapler design. Compared with dif-ferent structural designs, the sleeve anastomosis method is more reliable than the fit anastomosis method.

1. 引言

血管吻合技术作为外科手术的基石 [1]，应用于临床的血管吻合方法主要有缝合法、粘合法、针环法和激光焊接法等 [2]。多年来，国内外学者不断创新血管吻合技术，以期缩短吻合时间，提高血流通畅率。由于传统手工缝合技术操作复杂、吻合时间长且会造成内膜损伤等问题，无缝线的血管吻合器逐渐被运用到临床，但不可降解的吻合器会影响吻合口处血管正常收缩与舒张的生理功能 [3]，限制血管生长，同时还会引起无菌性炎症反应，增大血管阻塞风险。

近年来，可降解血管吻合器逐渐成为研究热点，研究人员不断探索各类可降解材料以期运用到血管吻合器中。广泛应用于血管、心肌等软组织再生的水凝胶 [4]，是一种具有亲水性的三维网状结构胶体，聚合物链之间的交联可以使水凝胶保持稳定的结构 [5]，与一些生物组织在温度、电场、PH值和酶的变化下的生物学、化学和物理表现较相似 [6]。Suo等 [7] 通过实验证明可生物降解的壳聚糖黏合剂可将水凝胶与软组织紧密粘合；Lv等 [8] 首次报道了在器官移植中使用水凝胶进行血管吻合的病例，为该领域开辟了新的方向。海藻酸钙(Calcium Alginate, CA)来源于巨型海藻，因其具有良好的生物相容性、止血性、降解性及抗菌性 [9]，可直接作用于伤口巨噬细胞，已广泛应用于再生医学、组织工程及支架药物释放等领域。初晓夏 [10] 等人的研究表明不同浓度梯度的海藻酸钙纤维敷料细胞毒性均为1级，无细胞毒性。海藻酸钙水凝胶在水性溶剂中易加工，具有可控降解的特性。Liu等 [11] 通过实验发现人脐静脉内皮细胞能够附着在海藻酸盐水凝胶支架上，并在水凝胶内形成新的血管网络；可见由海藻酸钙单体制备的水凝胶在血管等软组织再生方面有广阔的应用前景。

本文旨在设计一款新型血管吻合器应用于椎动脉重建术中。颈椎骨肿瘤通常根据起源和性质可分为良性骨肿瘤、恶性骨肿瘤、有恶性倾向的骨肿瘤、良性脊椎附属组织肿瘤及恶性脊椎附属组织肿瘤。对于良性肿瘤，可采取根治性放疗或选择性动脉栓塞治疗；对于恶性肿瘤，治疗或缓解其症状的首选方法是脊柱肿瘤全椎切除术 [12]。不论原发性肿瘤或转移性肿瘤，凡能耐受手术者均应尽早手术，以防止截瘫的发生，若切除不充分容易导致局部复发，压迫脊髓和神经根 [13]。椎骨置换手术过程如图1所示。将整个锥体切除，采用人工锥体置换，可重建颈椎稳定性，降低并发症发生概率 [14]。其中，椎动脉重建是椎骨置换术中恢复充足血流的一个重要环节。

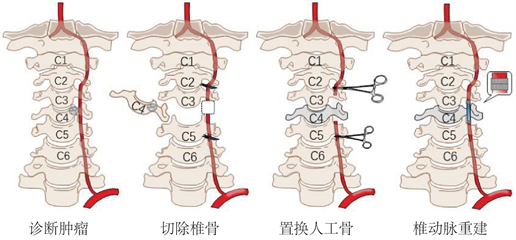
Figure 1. Vertebrae replacement surgery

图1. 椎骨置换手术过程

为了降低传统针线缝合对血管内皮造成的损伤以及机械吻合刚性结构对血管的束缚，本文提出基于海藻酸钙基水凝胶(Calcium Alginate Hydrogel, CAH)的血管吻合技术，设计了贴合式及袖套式两种椎动脉吻合模型，采用流固耦合(Fluid-Structure Interaction, FSI)方法，对比两种吻合模型中血管变形、血管壁面剪切力的分布情况，并进行离体爆破压实验，以探究两种吻合方法的优缺点。由于不同的吻合方法会影响吻合部位的血流动力学环境，进而影响急性血栓以及动脉粥样硬化等的形成，因此，针对不同吻合方式的对比分析对血管吻合技术具有重要的参考价值。

2. 材料与方法

2.1. 海藻酸钙水凝胶

本研究采用苏州凝智新材料发展有限公司制备的聚丙烯酰胺–海藻酸钙水凝胶(Polyacrylamide/Calcium Alginate Hydrogel, PAAm-CAH)进行实验。Hang等 [6] 已验证该水凝胶在磷酸盐缓冲盐水(Phosphate-Buffered Saline, PBS)和半胱氨酸混合的模拟体液中可完全降解。

弹性模量表示水凝胶保持结构完整性的能力 [15]，是表征水凝胶力学性能的主要参数，较大弹性模量的水凝胶可使吻合面不易被血液冲散而破裂。参考国标GB/T1701-2001，在室温下准备三块尺寸为30 mm × 2 mm × 10 mm的溶胀平衡试样，采用聚苯乙烯片将水凝胶固定于冲击试验机(UH6503)的夹具上，进行单轴拉伸实验，加载速度为2 mm/min，测试得到应力应变曲线，如图2(a)所示，λ为初始无应力拉伸长度，PAAm-CAH可拉伸至初始长度4倍不发生断裂现象。图2(b)为PAAm-CAH在拉伸实验中应变量为0~350%时对应的应力应变曲线，由图可以明显看出，由于水凝胶的超弹性，材料已明显呈现非线性关系。

2.2. 吻合器建模与有限元仿真计算

2.2.1. 椎动脉吻合模型建立

采用SolidWorks 2016 (Dassault Systems, U.S.A)软件对内直径为4 mm、管壁厚为0.3 mm的椎动脉血管建立长度为40 mm的贴合式及袖套式椎动脉吻合三维模型，分别如图3(a)、图3(b)所示，吻合处的水凝胶厚度均为1 mm。为简化后续有限元计算量并将结果清晰展示，仅建模了半个模型。

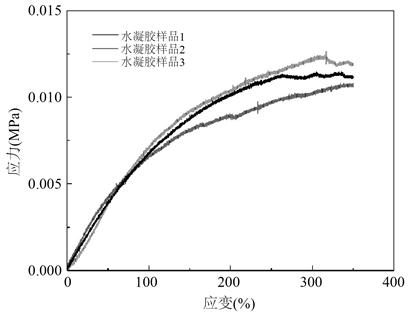(a)(b)

Figure 2. The elastic modulus of PAAm-CAH (a) tensile test of PAAm-CAH, (b) stress-strain curves of PAAm-CAH tensile test

图2. PAAm-CAH的弹性模量(a) PAAm-CAH拉伸实验；(b) PAAm-CAH拉伸实验应力应变曲线

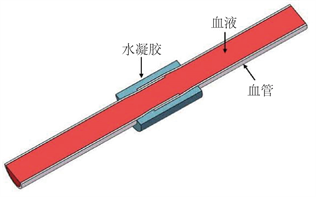(a) (b)

Figure 3. Vertebral artery anastomosis model (a) joint type, (b) sleeve type

图3. 椎动脉吻合模型(a) 贴合式；(b) 袖套式

2.2.2. 计算模型

血细胞黏附与血浆黏度使血液表现出非牛顿流体特性，本文选择Carreau-Yasuda黏度模型作表征血液的非牛顿行为 ^[16] ：

$\frac{\mu -{\mu }_{\infty }}{{\mu }_0-{\mu }_{\infty }}={\left[1+{\left(\lambda \gamma \right)}^z\right]}^{\frac{n-1}{z}}$ (1)

式中：μ为黏度(单位Pa∙s)； ${\mu }_0$ 为零剪切黏度，数值为2.2 × 10⁻² Pa∙s； ${\mu }_{\infty }$ 为无限剪切黏度，数值为2.2 × 10⁻³ Pa∙s； $\lambda$ 为时间，数值为3.313 s；n为模型指数，数值为0.3568 [17]；z为幂律指数，数值为0.644； $\gamma$ 为切应变率。

由于水凝胶具有超弹性，应变能密度函数能较好地表达超弹性材料的力学特性，文本采用Neo-Hookean模型对水凝胶的单轴拉伸实验数据进行拟合，表达式为：

$W=\frac{1}{2}\lambda {\left(\text{ln}J\right)}^2-\mu \text{ln}J+\frac{1}{2}\mu \left(I_1-3\right)$ (2)

式中：W为应变能； $\lambda$ 为伸长率；J为变形体积比值；μ为材料的应力量纲常数； $I_1$ 为拉伸方向上的张量不变量。对于Neo-Hookean超弹性材料，在小应变极限下，线弹性材料的材料常数与超弹性材料的材料常数是相同的。

此外，血液流动控制方程主要根据Navier-Stokes方程 [18] 求解，公式如下：

$\rho \frac{\partial u}{\partial t}+\rho \left(u·\nabla \right)u=\rho g-\nabla p+\mu {\nabla }^{2}u$ (3)

$\nabla ·u=0$ (4)

式中： $\rho$ 为血液密度； $u$ 为血流速度矢量；g为重力加速度矢量；t为时间；p为压力；μ为黏性系数。本模型设定血液密度ρ_f = 1056 kg/m³，粘度系数μ = 0.0035 Pa∙s [19]。将椎动脉管壁设置为均匀、各向同性线弹性材料，密度为1.15 × 10³ kg/m³，壁厚均为0.3 mm，弹性模量为1.7 MPa，泊松比为0.499 [20]。

本文计算模型通过软件ANSYS Workbench 19.2 (ANSYS, Pennsylvania, US)进行数值求解。

2.2.3. 网格划分

将X_T格式文件直接导入ANSYS Workbench 19.2中进行网格划分，网格大小及单元类型是保证耦合面迭代计算收敛性的主要原因。经过多次尝试，将两个模型均设置为体网格划分。其中，贴合式吻合模型的网格节点数为17,498，单元数量为87,726；袖套式吻合模型的网格节点数为59,726，单元数量为316,307。

2.2.4. 边界设定

将血管出入口内边缘设置固定约束，血管内壁面为流固耦合面，中轴线所在平面为对称面。假定血液充满血管，且血液与血管之间无相对滑移。口边界条件采用流速控制 [21]，在一个心动周期(0.8 s)内选取流速的最大值0.569 v/(m∙s⁻¹)进行瞬态分析；出口设置为压力出口，在环境大气压下(101325 Pa)的表压为0 [22]。基于入口最大速度和血管直径的雷诺数为289.6 (小于2000)，即血液在椎动脉中的流动属于层流状态。

2.2.5. 计算及结果后处理

创建双向流固耦合工程，在CFX求解器中运行，经过多次尝试，将流场和固体计算的总时间设置为1 s，最大时间步为0.1 s时，计算可达到收敛。

2.3. 爆破压测试实验

本实验采用的血管样品为9根自购的猪动脉血管，冷链运输时间为24 h。除正常血管需作为对照组，其余血管剪成2段，用水凝胶吻合器重新连接。

将吻合后40 mm的血管置于平台，如图4(a)所示，使用实验室自制装备测定爆破压 [23]。血管一端置入医用延长三通管连接量程为0~100 KPa (0~750.06 mmHg)的压力表，并妥善结扎固定，另一端使用止血夹闭合，如图4(b)所示；三通管另一端与充满水的500 ml注射器相连，形成密闭空间。推动注射器使血管逐渐膨胀，直到血管发生破裂，漏气瞬间的气压值定义为爆破压，记录此时测压装置的数值。

(a) (b)

Figure 4. Burst pressure test (a) anastomosed blood vessels, (b) explosion pressure test platform

图4. 爆破压实验(a) 吻合后的血管；(b) 爆破压实验设备

3. 结果与讨论

3.1. 有限元计算结果与分析

3.1.1. 血管

在0.5 s时刻，椎动脉的整个壁面位移达到最大，图5为贴合式及袖套式吻合模型的变形云图，其中(a)为贴合式血管吻合模型的变形云图，最大变形量约为0.2183 mm，约为血管壁厚的72.8%；(b)为袖套式血管吻合模型的变形云图，最大变形量约为0.27545 mm，约为血管壁厚的91.8%。

(a) (b)

Figure 5. The deformation distribution (a) deformation cloud map of fitting model, (b) deformation cloud image of sleeve fitting model

图5. 变形分布(a) 贴合式吻合模型的变形云图；(b) 袖套式吻合模型的变形云图

除此以外，血管吻合模型的壁面剪切应力分布均匀，贴合式血管吻合模型的壁面剪切应力平均值为8.7 × 10⁻⁵ MPa；袖套式血管吻合模型的壁面剪切应力最大值为4.9 × 10⁻⁵ MPa。

椎动脉位于锥孔之中，较大的变形会促使血管与椎骨接触产生摩擦，增大水凝胶吻合失败风险。贴合式与袖套式血管吻合模型变形量相差较小，且均不及血管壁厚的100%，有利于血管吻合的成功。壁面剪切应力(Wall Shear Stress, WSS) 体现的是血管内皮组织在血液流动时所受摩擦力，较大的壁面剪切力促使动脉内膜渗透性增加，内皮细胞脱落，中间层变薄，导致动脉瘤的形成 [24]；同时，过低的WSS会减少调节局部血流和防止内膜增生形成所需血小板聚集抑制剂的分泌，对血小板的活化和聚集有较大影响，是造成动脉粥样硬化的危险因素之一 [25]。由结果可知，袖套式血管吻合模型的WSS与贴合式血管吻合模型的WSS处于正常范围，能够避免动脉瘤的形成并降低动脉粥样硬化的风险。

3.1.2. 水凝胶

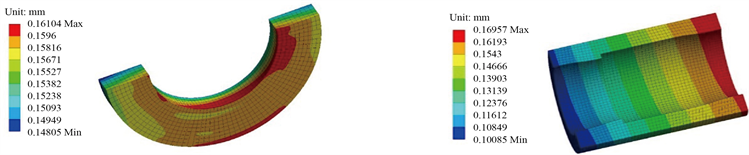
图6(a)、图6(b)为贴合式及袖套式吻合模型中水凝胶的变形云图，贴合式血管吻合模型中水凝胶的最大变形量约为0.16104 mm，袖套式血管吻合模型中水凝胶的最大变形量约为0.16957 mm。

从材料强度方面分析，应力高部位是材料最容易破坏的位置，即导致水凝胶吻合失败。由图6(c)、图6(d)可知，贴合式模型中水凝胶的最大应力、应变分别为119.77 Pa、2.4%，袖套式血管吻合模型中水凝胶所受应力较小，最大应力、应变分别为15.679 Pa、0.3%，能够降低血管吻合后水凝胶发生拉伸破坏的可能性，在整个计算过程中，二者的应力都处于很低的应力范畴，可以预计在较大血流周期中，水凝胶不会出现疲劳现象。

(a) (b)(c) (d)

Figure 6. Distribution of shear stress on vascular wall (a) Hydrogel deformation cloud image in fit vascular anastomosis model; (b) Hydrogel deformation cloud image in cuff vascular anastomosis model; (c) Hydrogel stress distribution in fitted vascular anastomosis model; (d) Hydrogel stress distribution in cuff vascular anastomosis model

图6. 血管壁面切应力分布(a) 贴合式血管吻合模型中水凝胶变形云图；(b) 袖套式血管吻合模型中水凝胶变形云图；(c) 贴合式血管吻合模型中水凝胶应力分布；(d) 袖套式血管吻合模型中水凝胶应力分布

3.2. 爆破压分析

贴合式及袖套式水凝胶血管吻合方式均能实现血管吻合，其中，贴合式吻合血管的爆破压与正常血管爆破压相差较大(见表1)。对比可知，袖套式吻合血管爆破压与正常血管爆破压相近，约为1321.1 mmHg (1 mmHg = 0.133 kPa)。

Table 1. Comparison of burst pressure between normal vessels and vessels after anastomosis (mmHg)

表1. 正常血管和吻合后血管爆破压比较(mmHg)

在本实验过程中，除正常血管外，其余在血管处爆裂的样本均不做统计，采用新样本继续实验，直至爆破部位位于水凝胶吻合处。成年人正常生理状态下的血压为60/80~100/120 mmHg，因此，采用袖套式水凝胶吻合血管的方法足够承受人体正常状态下的血压。

4. 结论

本文重点研究PAAm-CA复合水凝胶在血管吻合中的可靠性，为水凝胶在生物软组织再生方面提供力学参考。PAAm-CA复合水凝胶在血管吻合中的可靠性主要体现在吻合后血液对血管和水凝胶产生的变形及应力上。本文针对两种水凝胶血管吻合方式，应用FSI方法在1个脉动周期内选取最大血液流速进行仿真，研究椎动脉血流对吻合后血管的作用，并详细分析PAAm-CA复合水凝胶在血管吻合中的可靠性，主要研究结论是：

1) 分析血管可知，使用水凝胶吻合后的血管变形量均不及管壁厚的100%，能够保证血管生长过程中的稳定性；吻合后血管的WSS均处于正常范围，可更大程度保证椎动脉吻合的可靠性。

2) 分析PAAm-CA复合水凝胶可知，袖套式血管吻合模型中水凝胶所受应力应变较小，进一步降低水凝胶在吻合过程中发生断裂的可能。

3) 分析吻合后血管爆破压可知，袖套式水凝胶吻合的血管爆破压明显高于贴合式水凝胶吻合的血管爆破压，且与正常血管爆破压相近，能够达到预期血管重建的效果。

本文提出两种基于水凝胶的椎动脉吻合方法，运用FSI方法对PAAm-CA复合水凝胶椎动脉吻合模型进行仿真，主要对比变形及应力分布，探究不同吻合方法对血管及水凝胶的影响；搭建爆破压实验平台，将吻合后的血管与正常血管进行对比，证明水凝胶在软组织粘合方面的可靠性，对可降解血管吻合器的发展具有积极意义，同时，证明了袖套式吻合方法在水凝胶吻合血管方面有较大的优势。后将继续深入研究，对PAAm-CA复合水凝胶进行降解实验探究其降解周期，并设计该水凝胶血管吻合器的辅助操作工具，期望可降解水凝胶血管吻合器能够高效应用于生物体内，为血管吻合器研究做出有益的探索。

基金项目

国家自然科学基金项目(51735003)；2019年科技部数字诊疗装备研发计划(2019YFC0120402)；上海理工大学医工交叉基金。

NOTES

^*第一作者。

^#通讯作者。