三维固体稳态传热问题的等几何分析

Isogeometric Analysis for Steady-State Heat Transfer in Three-Dimensional Solid Problems

摘要: 在芯片微电子、增材制造等领域的机械结构设计中，设备的工作温度往往会影响整体性能，而等几何分析方法作为近年来比较热门的新型数值计算方法，在动力学以及流体力学领域已有部分应用。本文尝试发挥等几何分析不会损失几何精度的特点推展到三维稳态传热分析问题，利用多片拼接NURBS体参数化模型实现几何的多样性，并提出了对三维空间的等几何方式离散，以及对热传导及热对流两种状态下的数值分析结果。实验结果表明等几何分析法在大幅提高计算小效率的同时，在传热分析计算精度上能够等效于传统有限元方法。

Abstract: In the mechanical structure design of chip microelectronics, additive manufacturing and other fields, the working temperature of the equipment often affects the overall performance. The iso-metric analysis method, as a popular new numerical calculation method in recent years, has been partially applied in the field of dynamics and fluid mechanics. In this paper, this paper attempts to extend the characteristics of isometric analysis without loss of geometric accuracy to the three- di-mensional steady-state heat transfer analysis problem, uses multi-piece splicing NURBS body par-ametric model to achieve geometric diversity, and proposes the discretization of isogeometric methods in three-dimensional space and the numerical analysis results in heat conduction and heat convection. Experimental results show that the isometric analysis method can be equivalent to the traditional finite element method in terms of calculation accuracy of heat transfer analysis while greatly improving the calculation efficiency.

1. 引言

传热问题按传热方式的不同，分为热传导(导热)、热对流及热辐射三种，在机械设计中会直接影响产品的工作效率和性能，在各种工程问题的仿真中，常见的商业软件数值求解方法有以下三种：有限元法(FEM)、有限差分法(FDM)以及有限容积法(FVM) [1]，这三种方法都具有各自独特的空间和时间的离散化方法，系统方程的离散方式和矩阵求解方法。其中有限元法应用最为广泛，在解决传热问题时对不规则的域或边界有良好的适应性。等几何方法作为近些年涌现出的新数值计算方法 [2]，它同时包含了有限元方法及无网格法的优点：首先等几何方法通过NURBS样条的自然参数域的划分以代替网格划分，减少分析的工作量；同时等几何分析统一了几何模型与分析模型，对于结构优化、大变形模流分析及网格细化等问题，可以节省计算机辅助设计的精确建模与计算机仿真的网格模型之间的数据交换 [3] [4]。目前等几何已在板壳 [5]、振动 [6]、接触分析 [7] 及流体等领域被成功应用，但主要都是针对他们的力学性能研究 [8]。本文旨在利用多片等几何方法实现三维稳态热传导和热对流两种问题的分析求解，并与目前商业有限元的结果对比，证明了等几何在处理多片传热问题的可行性。

2. 等几何热分析的模型构建

2.1. NURBS基础理论

等几何分析方法的基本思想是在建模和分析使用统一的几何模型表示，目前CAD系统通常将非均匀有理B样条(NURBS)用于几何表达，并使用形函数代替有限元的基函数。两者的相同之处在于他们都采用了伽辽金变分原理。在进行等几何分析时，对于二维平面或板壳NURBS模型，表达式如下：

$S\left(\xi ,\eta \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{R}_{i,j}^{p,q}\left(\xi ,\eta \right)P_{i,j}}}$ (1)

式中p、q分别表示ξ、η两个方向上的基函数次数，n × m个控制点P_ij生成控制网格，对于二维平面问题 $d_{ij}\in R^2$ ，对于板壳曲面 $d_{ij}\in R^3$ ， $\omega$ 是基函数对应的权重。同理可以将上述NURBS曲面推广到等几何三维实体，用三个节点矢量定义张量积样条，样条表达式如下：

$V\left(\xi ,\eta ,\varsigma \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{\displaystyle \underset{k=1}{\overset{l}{\sum }}{R}_{i,j,k}^{n,m,l}\left(\xi ,\eta ,\zeta \right)P_{i,j,k}}}}$ (2)

其中形函数R的表达式如下：

$R_{i,j,k}^{p,q,r}\left(\xi ,\eta ,\xi \right)=\frac{N_{i,p}\left(\xi \right)M_{j,q}\left(\eta \right)Q_{k,r}\left(\zeta \right){\omega }_{ijk}}{{\displaystyle \underset{i=1}{\overset{l}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{\displaystyle \underset{k=1}{\overset{n}{\sum }}{N}_{i,p}\left(\xi \right)M_{j,q}\left(\eta \right)Q_{k,r}\left(\zeta \right){\omega }_{ijk}}}}}$ (3)

以一个NURBS体单元为例，其控制点数量为L，基函数向量序列为：

$R=\left(R_1,R_2,\cdots ,R_L\right)$ (4)

各控制点的处的基函数表达为：

$R_s=M_i{N}_j{Q}_k$ (5)

$s=\left(k-1\right)mn+\left(j-1\right)n+i$ (6)

其中

$i=1,2,\cdots ,n$ ； $j=1,2,\cdots ,m$ ； $k=1,2,\cdots ,l$ (7)

该单元的几何张量场的插值形式为：

$G_e\left(\xi ,\eta ,\zeta \right)=P_e^{\text{T}}R$ (8)

$P_e=\left(\begin{array}{ccc}{x}_1& y_1& z_1\\ x_2& y_2& z_2\\ ⋮& ⋮& ⋮\\ x_L& y_L& z_L\end{array}\right)$ (9)

2.2. 多片模型构建

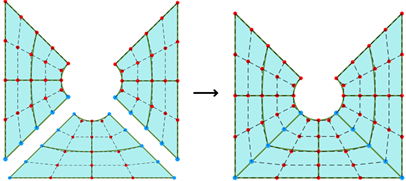
由于目前大部分CAD模型采用边界表示法(B-Rep)表达精准的几何模型 [9]，而等几何分析需要在几何体内部同时生成控制点及网格，因此将CAD模型转化成分析可用的样条格式使现在和未来都值得深入的研究，也是等几何难以冲击传统有限元的瓶颈所在。对于相对复杂的模型，本文通过引入片(Patch)的概念并将多个片进行拼接，从而实现一个非四边形或非六面体的NURBS模型的建立 [10]。如图1所示，我们假设(b)所表示的物理域Ω是由N_ptc = 3的并集组成的，那么其表示方式为 $\bar{\Omega }={\displaystyle {\cup }_{i=1}^{N_{\text{ptc}}}{\bar{\Omega }}_i}$ ，(b)中蓝色标注控制点的区域，即每个片的公共面上的边界函数需要一一对应且与之对应的节点矢量相同才能使模型的离散空间保证连续。在GeoPDEs等现有开源等几何分析代码中需要对每个片面的公共边界编号以检索边界，实验证明在宏观尺寸下，直接通过在对整个Ω物理域控制点排序的过程中对比控制点坐标及权重信息同样可以判断这些片与片之间重合的控制点。

(a) (b)

Figure 1. NURBS planar multi-piece stitching

图1. NURBS平面多片拼接

2.3. 参数域划分

等几何分析继承了有限元中等参单元的思想，由于NURBS体的基函数有节点矢量定义，张量积样条的节点适量可以与参数域的规则网格相对应，这一特点使等几何分析无序对几何模型再进行网格剖分的工作，只需要通过节点即可剖分分析对象的物理域模型。同时NURBS基函数具有局部支撑性，即在一个参数区间 $\left[{\xi }_i,{\xi }_i{}_{+\text{1}}\right]$ 中至多有p + 1个基函数非零，在经过伽辽金法离散后生成的刚度矩阵为稀疏矩阵。因此我们可以把等几何分析的单元定义为节点之间测度非零的间隙，节点则定义为单元各顶点的控制点。以图2(a)例，一个由两片二维张量积样条组成的二次NURBS平面，通过将各方向控制点数量为3的两个片通过一次k-均值细化成5 × 5，图中的绿色实线条为模型的单元剖分，不难看出单元内非零基函数为 $\left(p+1\right)\times \left(q+1\right)=9$ 个，其中p和q为各方向基函数的次数。当我们有限元法做温度场求解时，首先需要得到形函数的偏导数，可以根据复合函数的求导法并稍作转化，便可获得：

$\left[\begin{array}{c}\frac{\partial N_i}{\partial \tilde{\xi }}\\ \frac{\partial N_i}{\partial \tilde{\eta }}\end{array}\right]=\left[\begin{array}{cc}\frac{\partial x}{\partial \tilde{\xi }}& \frac{\partial y}{\partial \tilde{\xi }}\\ \frac{\partial x}{\partial \tilde{\eta }}& \frac{\partial y}{\partial \tilde{\eta }}\end{array}\right]\left[\begin{array}{c}\frac{\partial N_i}{\partial x}\\ \frac{\partial N_i}{\partial y}\end{array}\right]=J\left[\begin{array}{c}\frac{\partial N_i}{\partial x}\\ \frac{\partial N_i}{\partial y}\end{array}\right]$ (10)

在等几何中基函数代替了形函数，上式中的雅可比矩阵J即可转化为：

$J=\left[\begin{array}{cc}\frac{\partial x}{\partial \tilde{\xi }}& \frac{\partial y}{\partial \tilde{\xi }}\\ \frac{\partial x}{\partial \tilde{\eta }}& \frac{\partial y}{\partial \tilde{\eta }}\end{array}\right]=\left[\begin{array}{cc}{\displaystyle \underset{i=1}{\overset{9}{\sum }}\frac{\partial R_i}{\partial \xi }{x}_i}& {\displaystyle \underset{i=1}{\overset{9}{\sum }}\frac{\partial R_i}{\partial \xi }{y}_i}\\ {\displaystyle \underset{i=1}{\overset{9}{\sum }}\frac{\partial R_i}{\partial \eta }{x}_i}& {\displaystyle \underset{i=1}{\overset{9}{\sum }}\frac{\partial R_i}{\partial \eta }{y}_i}\end{array}\right]*\left[\begin{array}{cc}\frac{1}{2}\left({\xi }_{i+1}-{\xi }_i\right)& 0\\ 0& \frac{1}{2}\left({\eta }_{j+1}-{\eta }_j\right)\end{array}\right]$ (11)

为了便于代码的实现，我们将矩阵J乘号左右两边的部分拆分为J₁、J₂，分别代表图2中物理域(a)与参数域(b)之间的映射关系以及参数域到母域(c)之间的映射关系。如图2(b)为一个单片的参数域展示，每一个单元的顶点都有一个相对应的节点矢量，在计算机实现参数坐标到母单元坐标变换时，其对应的坐标变换行列式为：

$\left|J_2\right|=\left({\xi }_{i+1}-{\xi }_i\right)\left({\eta }_{j+1}-{\eta }_j\right)/4$ (12)

对于三维问题只需要对上述矩阵增加一个维度即可，这里不多做赘述。

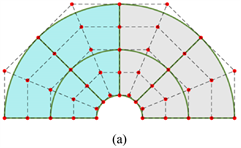
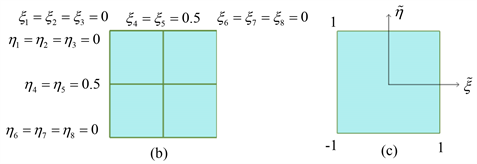
Figure 2. Physical domain, parameter domain and parent domain coordinates

图2. 物理域、参数域和母域坐标

3. 稳态传热问题的等几何分析推导

3.1. 等几何推导

常见传热问题可以分为热传递、热对流以及热辐射三种，本文主要对前两者的稳态问题展开研究。三维固体瞬态热传导方程如下 [11]：

$\rho c\frac{\partial T\left(x,y,z,t\right)}{\partial t}=\left(k_x\frac{{\partial }^{2}T}{\partial x^2}+k_y\frac{{\partial }^{2}T}{\partial y^2}+k_z\frac{{\partial }^{2}T}{\partial z^2}\right)+Q\left(x,y,z,t\right)$ (13)

其中 $Q\left(x,y,z,t\right)$ 是固体内部热产生的速率，ρ是密度，c是比热容，k_x、k_y和k_z分别表示各方向的导热系数，稳态问题可以省略时间域的影响，可以将方程简化为：

$k_x\frac{{\partial }^{2}T}{\partial x^2}+k_y\frac{{\partial }^{2}T}{\partial y^2}+k_z\frac{{\partial }^{2}T}{\partial z^2}=Q\left(x,y,z\right)$ (14)

因此在稳态问题的研究中我们可以忽略材料的密度及比热容所带来的影响，对于边界条件可以表示为以下三类：

狄利特雷边界： ${T|}_{\Gamma }=T_{\text{k}}$

纽曼边界条件： $-{k\frac{\partial T}{\partial n}|}_{\Gamma }=q_0$

罗宾边界条件： ${k\frac{\partial T}{\partial n}|}_{\Gamma }=h_{\text{c}}\left(T-T_{\infty }\right)$

其中T₀是起始温度，T_k是已知温度，T_∞为环境介质温度，q₀是规定边界的热通量，h_c是对应的对流系数。

根据第一章等几何理论的描述可知对模型进行离散化的过程中单元内的形函数我们用NURBS基函数代替，同时温度场是一种标量计算，每个控制点的自由度为1，因此几何矩阵B_e的定义如下：

$B_e=\left[\begin{array}{cccc}\frac{\text{d}{R}_1}{\text{d}x}& \frac{\text{d}{R}_2}{\text{d}x}& \cdots & \frac{\text{d}{R}_L}{\text{d}x}\\ \frac{\text{d}{R}_1}{\text{d}y}& \frac{\text{d}{R}_2}{\text{d}y}& \cdots & \frac{\text{d}{R}_L}{\text{d}y}\\ \frac{\text{d}{R}_1}{\text{d}z}& \frac{\text{d}{R}_2}{\text{d}z}& \cdots & \frac{\text{d}{R}_L}{\text{d}z}\end{array}\right]$ (15)

其中L为单元所含的控制点数目。值得注意的是，尽管稳态问题省略了热容及密度的影响，但我们仍需要对赋予第三边界条件的平面做一个局部表面传热计算并添加在等式右侧以确保边界上的热通量对整个传热系统方程的影响。结合上述热传导方程及边界条件，通过伽辽金变分原理我们可以获得他的等效积分形式：

$\left(K_t+N_t\right)\left\{T\right\}=\left\{Q_t\right\}+\left\{Q_c\right\}$ (16)

式中的矩阵的意义及计算方法分别为：

温度场刚度矩阵：

$K_t={\displaystyle \underset{\Omega }{\int }{B}^{\text{T}}\left[\begin{array}{ccc}{k}_x& 0& 0\\ 0& k_y& 0\\ 0& 0& k_z\end{array}\right]B\cdot J_1{J}_2\text{d}\Omega }$ (17)

局部表面传热矩阵：

$N_t={\displaystyle \underset{\Omega }{\int }{h}_{\text{c}}\cdot R^{\text{T}}R\cdot J_1{J}_2\text{d}\Omega }$ (18)

不同边界条件下等效表面热源载荷矩阵：

$Q_t=Q\cdot {\displaystyle \underset{{\Omega }_h}{\int }{R}^{\text{T}}{J}_1{J}_2\text{d}{\Omega }_h}$ (19)

$Q_c={\displaystyle \underset{{\Omega }_h}{\int }{R}^{\text{T}}{h}_{\text{c}}\left(T_{\infty }-T\right)\cdot J_1{J}_2\text{d}{\Omega }_h}$ (20)

其中h_c是边界热通量，Q代表热源，R是NURBS基函数，J₁为物理域到参数域的雅各比变换矩阵，J₂为母域到参数域的雅各比变换矩阵，T为域内所有节点的温度场向量，T_∞为环境温度，对于三维传热问题的研究，Ω_h表示边界条件施加的边界面。

3.2. 程序实现

上文展示了等几何传热问题的系统方程离散化及各个矩阵的计算方法，同样在1.3章节中介绍了多片NURBS模型及其参数域的划分，因此在程序设计的过程中我们不仅需要像有限元一样在每个单元内完成各项物理矩阵的计算，还需要对每一片的结果进行组装。如图3的流程所示，我们将每个NURBS片的几何信息及它的边界信息分别存放在两个类型的结构体中，为了提高计算效率可以让最终系统方程所需的全局矩阵做并行运算，方程的求解则可以通过将K转化为稀疏矩阵节省内存空间并对赋予第一边界条件的控制点对应得维度进行省略。

Figure 3. Program implementation flow

图3. 程序实现流程

4. 算例分析

本文分别针对热传递问题和热对流问题给出两个三维算例，充分验证了等几何方法得适用性，由于目前等几何分析还没有进入商业软件领域，本文的等几何分析方法的算例皆由MATLAB实现，实验结果对比选取COMSOL Multiphysics的有限元方法进行比较。主要从分布及部分参考点的温度以及特殊表面温度变化等方面进行对比。

4.1. 算例一

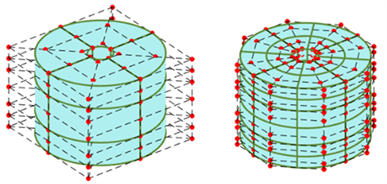
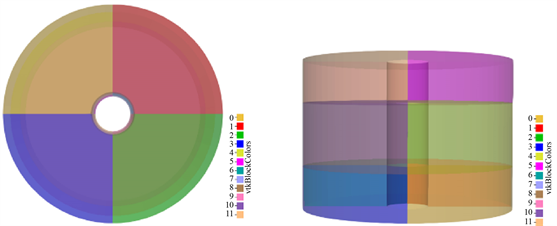
本算例为一个完全的三维圆筒模型，其物理属性及边界条件如表1所示，高为0.14米，内圆的直径为0.04米，外圆的直径为0.2米，如图4所示，通过将模型分成12片以实现对圆筒内高度区间在0.04至0.1米部分的内圆表面区域的热源施加，其分片状态如图5所示。用于对比的COMSOL Multiphysics有限元模型选择全局极细化网格单元大小，软件显示域单元数量为1144427。NURBS建模中的剖分功能使等几何模型的网格可以类似有限元方法，根据问题的需要进行相对应的划分。

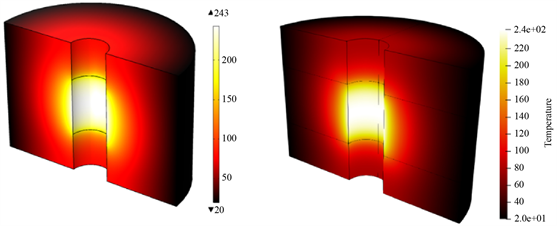
首先是模型及网格的建立，以各方向控制点数量为3的二次NURBS体建立圆筒的基本几何造型，各方向节点矢量分别为 $U=\left\{0,0,0,1,1,1\right\}$ 、 $V=\left\{0,0,0,1,1,1\right\}$ 和 $W=\left\{0,0,0,1,1,1\right\}$ ，经过两次k均值细化后的模型结果如图4(b)和图4(c)所示。经2次细化后各方向节点矢量均为{0, 0, 0, 0.25, 0.5, 0.75, 1, 1, 1}，即每片中包含了64个单元，每个单元由27个控制点组成。计算结果的温度分布如图6所示，为了更直观的数据对比我们选取坐标为(0, 0.02, 0.07)、(0, 0.02, 0.1)、(0, 0.02, 0.14)和(0, 0.06, 0.14)的四个特征参考点对比，结果如表2所示，实验结果表明当圆筒模型在进行两次细化后即可获得较高精度的计算结果，由于建模后网格信息可以直接生成，因此计算的时间复杂度也大幅度降低。

(a) (b)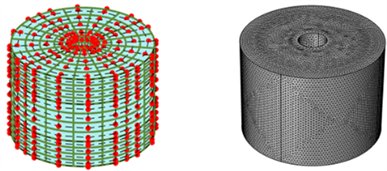(c) (d)

Figure 4. Three-dimensional cylinder and isogeometric models and fine finite element mesh. (a) k = 0; (b) k = 1; (c) k = 2; (d) Finite element mesh

图4. 三维圆筒等几何模型及精细有限元网格。(a) k = 0；(b) k = 1；(c) k = 2；(d) 有限元网格

(a) (b)

Figure 5. 3D cylinders and isogeometric models slice

图5. 三维圆筒等几何模型分片

(a) (b)

Figure 6. Temperature distribution. (a) Very fine mesh finite element results; (b) Isogeometric results

图6. 温度分布。(a) 极精细网格有限元结果；(b) 等几何结果

Table 1. Parameters and properties of algorithm 1

表1. 算例1的参数及属性

Table 2. Parameters and properties of algorithm 1

表2. 算例1的参数及属性

4.2. 算例二

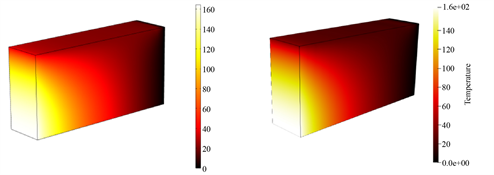
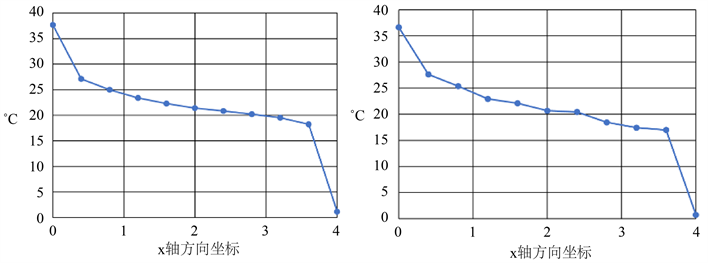
本文给出了一个基于存在对流边界问题的三维单片等几何分析案例，该算例仅由单片构成，几何模型各方向均采用二次NURBS样条并最终k均值细化两次，其物理属性和边界条件如图7所示，这里我们不再对模型的细节做介绍。图8的数值分布表明在含对流边界的温度场计算结果与有限元近似。重点观察赋予热通量的边界，即长方体顶部表面沿x轴方向的温度变化。由图9可以看出对流边界的温度变化，受外接温度影响，精细网格有限元结果和二次细化后的等几何结果都在20℃左右浮动，并且等几何在节点数量远小于有限元结果的情况下依然可以在边界上获得一条过渡平滑的曲线。

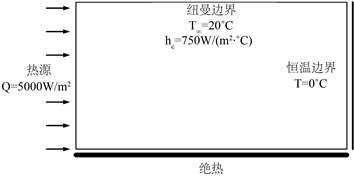
Figure 7. Definition of three-dimensional convective heat transfer problem

图7. 三维对流传热问题定义

(a) (b)

Figure 8. Temperature distribution. (a) Very fine mesh finite element results; (b) Isogeometric results

图8. 温度分布。(a) 极精细网格有限元结果；(b) 等几何结果

(a) (b)

Figure 9. Convective surface temperature change. (a) Very fine mesh finite element results; (b) Isogeometric results

图9. 对流面温度变化。(a) 极精细网格有限元结果；(b) 等几何结果

5. 结束语

本文将等几何方法运用并拓展到三维稳态的传热问题中，并与商业软件的极高精细网格划分下的分析结果进行对比，表明了该方法的可行性。等几何以NURBS体的基函数代替有限元的形函数，使分析网格可以更加精准、高阶光滑地表达模型的几何边界，同时等几何也可以在较少的节点数量下获得与精确解高度近似的结果。同时等几何分析统一了建模与仿真的所有模型的参数化工作，减少了数据处理量并提高了计算速度，为铸件冷却及热流耦合等多物理场问题的拓展奠定基础。后续工作将本文方法推广到热应力及相关结构优化上，充分发挥等几何在几何表达及高阶连续的特点并实现计算获得的形变结果直接反映在几何模型上。