下肢外骨骼助力机构及滑模步态轨迹跟踪控制方法

Lower Extremity Exoskeleton Assisted Mechanism and Sliding Mode Gait Tracking Control Method

摘要: 构建高精度下肢外骨骼步态方法有助于下肢康复效果的提升。针对下肢外骨骼辅助残疾患者康复治疗时电机跟踪精度不足的问题，基于下肢结构建立动力学模型，并设计线性执行机构驱动的外骨骼结构模型。为提高步态输出精度，减小外骨骼工作时外部干扰的影响，设计了一种结合非线性干扰观测器(Nonlinear Disturbance Observer, NDO)的滑模(Sliding Mode Control, SMC)控制方法，并使用优化器对控制模型参数全局寻优，获得最优反演滑模控制律参数。通过比较SMC与NDO-SMC在引入干扰信号下的跟踪精度，发现NDO方法可有效减少外部干扰的影响，使跟踪精度提升31%；比较SMC与AO-SMC控制器的轨迹跟踪误差，优化器相较于遗传算法在控制算法参数收敛速度方面有较大提升，并使步态轨迹跟踪精度提升了63%。

Abstract: The construction of high precision lower limb exoskeleton gait method is helpful to improve the lower limb rehabilitation effect. Aiming at the problem of insufficient motor tracking accuracy in the rehabilitation treatment of patients with disabilities assisted by lower limb exoskeleton, a dy-namic model was established based on lower limb structure, and a linear actuator driven exoskele-ton structure model was designed. In order to improve the accuracy of gait output and reduce the influence of external Disturbance in exoskeleton operation, a Sliding Mode Control (SMC) method combining Nonlinear Disturbance Observer (NDO) is designed. The optimizer is used to globally op-timize the parameters of the control model to obtain the optimal inversion sliding mode control law parameters. By comparing the tracking accuracy of SMC and NDO-SMC in the presence of interfer-ence signals, it is found that the NDO method can effectively reduce the influence of external inter-ference and improve the tracking accuracy by 31%. Comparing the trajectory tracking errors of SMC and AO-SMC controller, compared with genetic algorithm, the optimizer greatly improves the con-vergence speed of control algorithm parameters, and improves the gait trajectory tracking accuracy by 63%.

1. 引言

为避免中风患者在中风后发生痉挛、肌肉萎缩甚至永久性残疾，适当的康复治疗是必不可少的 [1]。康复治疗师资源有限，已有多种下肢外骨骼被应用于患者康复治疗 [2]。下肢外骨骼是一种辅助下肢运动的助力装置，其通过使用电力或储能元件为下肢关节提供动力，以协助膝关节与髋关节在矢状面上的屈伸，可用于肌肉力量康复或增强负重能力。由于下肢外骨骼在使用时易受到来自使用者肢体的干扰，使输出步态轨迹产生偏差，影响康复治疗效果，故有必要对其进行优化 [3]。

对类似下肢外骨骼的非线性系统，使用滑动模式控制(Sliding Mode Control, SMC)的方法可得到较好的跟踪效果 [4] [5]，相比PID方法在电机转矩控制方面有更高的精确性 [6]。然而，外部随机干扰和执行器故障在实际应用中普遍存在 [7]。针对这一问题研究人员使用了趋近律 [8] 等方法，但也遇到了难以兼顾控制效果、结构复杂，稳定性低等问题。为了改进控制器对随机扰动的补偿机制，文献 [9] 中提出了一种基于非线性扰动观测器的滑模控制(NDO-SMC)方案。同时在滑模控制及其各类改进控制方法中普遍存在多个设计参数，对参数的选定直接影响到整个系统的控制效果 [10]。目前广泛使用如遗传 [11] 、粒子群 [12] 、蚁群 [13] 等经典算法可有效优化设计参数，有效消除系统的不确定性。但不同优化算法存在收敛缓慢、陷入局部最优解等常见问题 [14]。各类算法的混合方法被相继开发以作弥补 [15]，如混合粒子群与遗传算法的PSO-GA方法 [16] 优化四自由度的下肢外骨骼PID控制器参数，改善了遗传算法收敛缓慢的特点，但该类优化方法不具有广泛的适用性，更适合解决特定问题。

针对以上下肢外骨骼控制轨迹跟踪中遇到的问题，本文提出一种基于滑模控制的下肢外骨骼步态轨迹跟踪控制方法。设计滑模控制方法(Sliding Mode Control, SMC)与非线性干扰观测器(Nonlinear Disturbance Observer, NDO)减少滑模控制抖振现象与估计外部干扰。另外针对难以选定最优设计参数的问题，本文创新性得使用Aquila参数优化器 [17] 优化控制参数，提高整个系统的控制效果，该算法根据迭代过程的推进分别设计四种迭代方法，兼顾了寻找最优解过程中的寻优范围与速度。

2. 下肢外骨骼助力机构

下肢外骨骼整体组成部分如图1所示，主要结构部件包括背部连接支架、髋关节助力机构、膝关节助力机构、踝关节固定机构等，助力结构主要符号说明如表1所示。本章分析了助力机构中各零件的连接与位置关系，建立电机位置输出与助力机构姿态的联系，作为后续步态控制的理论基础。下肢外骨骼助力机构原理图如图2所示。

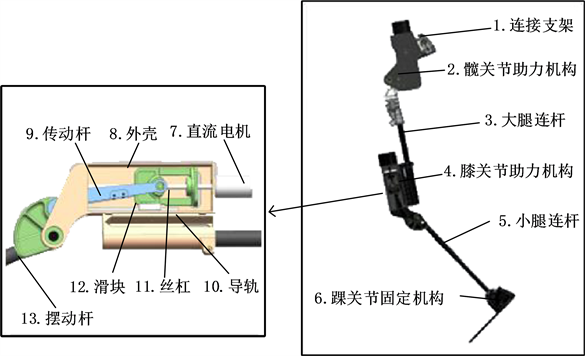
Figure 1. 3D model of lower limb exoskeleton

图1. 下肢外骨骼三维模型

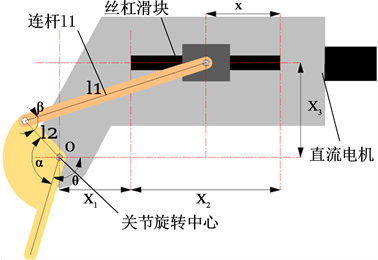
Figure 2. Schematic diagram of lower extremity exoskeleton structure

图2. 下肢外骨骼结构原理图

图2中，直流电机作为动力源，丝杠滑块机构带动连杆 $l_1$ ，以带动关节旋转中心O点旋转。滑块位置x与关节摆角 $\theta$ 的关系可表示为：

$\begin{array}{l}x=f\left(\theta \right);\\ f\left(\theta \right)=x_1+x_2+\sin \left(\frac{\pi }{2}+\theta -\alpha \right)\cdot l_2-\sqrt{l_1^2-{\left[x_3-\cos \left(\frac{\pi }{2}+\theta -\alpha \right)\cdot l_2\right]}^2}\end{array}$ (1)

Table 1. Power assist structure symbol description

表1. 助力结构符号说明

$\gamma$ 为传动杆 $l_1$ 与摆动杆 $l_2$ 之间的夹角，表示为：

$\gamma =\frac{\pi }{2}-\arccos \left(\frac{O{B}^2+l_1^2-l_2^2}{2\cdot l_1\cdot OB}\right)-\arctan \left(\frac{x_1+x_2-x}{x_3}\right)$ (2)

考虑助力机构活动范围与电机转速限制，本研究设计对应的结构设计参数，见表2。

Table 2. Structural dimension parameters

表2. 结构尺寸参数

3. 滑模步态轨迹跟踪控制方法

下肢外骨骼控制方法逻辑如图3所示，其中理论轨迹y由公式1中滑块位置与关节摆角的转换关系为基础进行设计。控制过程主要由滑模控制器、非线性干扰观察器(NDO)与Aquila优化器组成，其中：滑模控制器接收轨迹信息，生成电压控制电机转动；NDO观察受到干扰的下肢外骨骼轨迹跟踪精度，实时调整以减少滑模控制中的抖振；Aquila参数优化器迭代优化NDO中的设计参数，进一步提高跟踪精度。

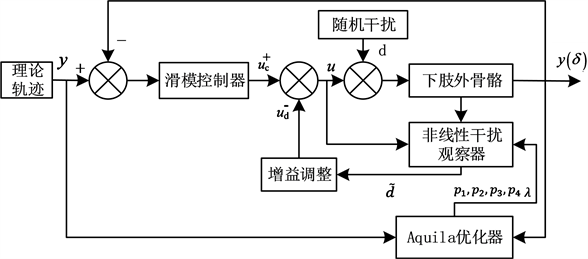
Figure 3. Control diagram of lower limb exoskeleton

图3. 下肢外骨骼控制图

3.1. 非线性干扰观测器(NDO)设计

首先，将步态轨迹状态方程描述为如下向量形式：

$\stackrel{\dot{}}{x}=F\left(x\right)+H\left(x\right)u_f+D\left(x\right)d$ (3)

其中 $F\left(x\right)=\left[\begin{array}{c}{x}_2\\ g\left(x_3\right)\end{array}\right]$ ， $H\left(x\right)=\left[\begin{array}{c}0\\ \begin{array}{c}⋮\\ 0\end{array}\end{array}\right]$ ， $D\left(x\right)=\left[\begin{array}{c}0\\ \begin{array}{c}⋮\\ 1\end{array}\end{array}\right]$。

$\{\begin{array}{l}\hat{d}=v+p\left(x\right)\\ \stackrel{\dot{}}{v}=-K\left(x\right)\left(F\left(x\right)+H\left(x\right)u_f+D\left(x\right)\left(v+p\left(x\right)\right)\right)\end{array}$ (4)

式中，p为大于0的常数；定义NDO的观测误差为，的时间导数可表示为：

$\tilde{d}=d-\hat{d}\approx K\left(x\right)\left(F\left(x\right)+H\left(x\right)u_f+D\left(x\right)\left(v+p\left(x\right)\right)\right)-K\left(x\right)\stackrel{\dot{}}{x}=-p_4{\tilde{d}}^2$ (5)

为使NDO的运动轨线在有限时间内到达切换面，选择如下李雅普诺夫函数 [8] ：

$V_0=\frac{1}{2}{\tilde{d}}^2$ (6)

$V_0$ 的时间导数是：

${\stackrel{\dot{}}{V}}_0=\tilde{d}\stackrel{\dot{}}{\tilde{d}}=-p_4{\tilde{d}}^2$ (7)

可得到 ${\stackrel{\dot{}}{V}}_0<0$ ，因此可知NDO线性稳定。NDO的输出变量定义为：

$u_d=\frac{1}{h\left(x\right)}\hat{d}$ (8)

3.2. 滑模控制器设计

使用非线性干扰观测器后，该系统用公式(3)表示的子系统可使用下式表示：

$\begin{array}{c}{x}_2=f\left(x\right)+h\left(x\right)u+D\\ =f\left(x\right)+h\left(x\right)\left(u_d-u_{do}\right)+D\left(x\right)\\ =f\left(x\right)+h\left(x\right)u_d-\hat{D}+D\\ =f\left(x\right)+h\left(x\right)u_d+\tilde{D}\end{array}$ (9)

由上式可观察到系统扰动由变为，公式(9)可简化为：

$\begin{array}{l}y=x_1\\ {\stackrel{\dot{}}{x}}_1=x_2\\ {\stackrel{\dot{}}{x}}_2=f\left(x\right)+h\left(x\right)u_{sb}+\tilde{D}\end{array}$ (10)

系统误差可以定义为：

$\begin{array}{l}{e}_1=y-y_d\\ e_2=x_2+k_1{e}_1-{\stackrel{\dot{}}{y}}_d\end{array}$ (11)

式中为设计轨迹位置，为实际轨迹位置。取滑动面的一般形式 [13]，定义滑动面为：

$s=c_1{e}_1+e_2;c_1>0.$ (12)

假设对于所有，存在任意正常实数使得方程成立。自适应率采用：

$\stackrel{\dot{}}{\hat{\delta }}=\lambda \left|s\right|$ (13)

式中为设计参数；控制率为：

$u_s=\frac{c_1\left(k_1{e}_1-e_2\right)-f\left(\theta \right)+{\stackrel{\dot{}}{a}}_1\left(x_1\right)-e_1-hs-\hat{\delta }\mathrm{sgn}\left(s\right)}{b}$ (14)

为保证系统稳定的控制效果，以下证明系统控制率的稳定性。选择与公式(6)相同的李雅普诺夫函数：

$V=\frac{s^2}{2}$ (15)

对函数求关于时间的导数，得到：

$\stackrel{\dot{}}{V}=\stackrel{\dot{}}{s}\cdot s$ (16)

将公式(12)代入上式可得：

$\stackrel{\dot{}}{V}=\left[\hat{d}-\hat{\delta }\left(t\right)-\rho \mathrm{sgn}\left(\hat{s}\right)\right]\hat{s}$ (17)

故可得该李雅普诺夫函数关于时间的导数，既可推得系统是稳定的。

3.3. 使用Aquila优化器优化设计参数

本节使用Aquila优化器优化非线性干扰观测模型、公式(11)与公式(16)中的设计参数()。Aquila算法模拟自然界中猛禽捕食的过程，由最优解范围探测及最优解捕获两部分组成，具有较快的收敛速度与更大的搜索范围。算法步骤如图4所示。

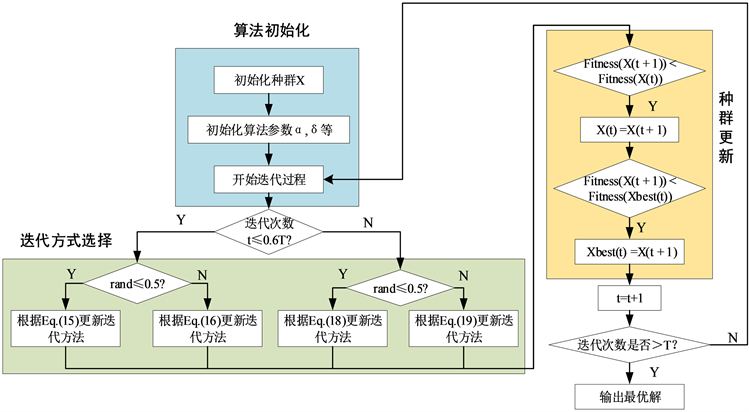
Figure 4. Optimization process of Aquila optimizer

图4. Aquila优化器寻优过程

3.3.1. 最优解范围探测

在探索空间选择过程中通过迭代选择最佳的求解范围，该迭代过程表示为：

$X_1\left(t+1\right)=X_{best}\left(t\right)\times \left(1-\frac{t}{T}\right)+\left(X_M\left(t\right)-X_{best}\left(t\right)\times rand\right)$ (18)

式中t与T分别表示迭代的当前次数与最大迭代次数；表示当前迭代最优解，表示当前迭代参数平均值；rand是取值为[0, 1]间的一个随机值。

确定最优解所在范围后，通过在最优解近似位置等高盘旋的方式对最优解选定区域进行小范围的探索，该迭代过程可表示为：

$X_2\left(t+1\right)=X_{best}\left(t\right)\times Levy\left(D\right)+X_R\left(t\right)+\left(y-x\right)\times rand$ (19)

式中D是种群维数空间，称为飞行分步函数 [17]，表示为：

$Levy\left(D\right)=s\times u\times \frac{\sigma }{{\left|v\right|}^{\frac{1}{\beta }}}$ (20)

其中s取值为0.01；u与v为取值为[0, 1]间的一个随机数，为表达盘旋行为的螺旋线函数。

3.3.2. 最优解范围探测

在确定最优解所在范围后，模仿猛禽的俯冲行为，对最优解快速逼近，可表示为：

$X_3\left(t+1\right)=\left(X_{best}\left(t\right)-X_M\left(t\right)\right)\times \alpha -rand+\left(\left(UB-LB\right)\times rand+LB\right)\times \delta$ (21)

式中UB表示给定变量的上边界，LB表示给定变量的下边界， $\alpha$ 与为开采调整参数，最小值取0.1。最后在迭代过程靠近最优解时，根据最优解在迭代过程中的随机变化抓取最优解精确值，可表示为：

$X_4\left(t+1\right)=QF\times X_{best}\left(t\right)-\left(G_1\times X\left(t\right)\times rand\right)-G_2\times Levy\left(D\right)+rand\times G_1$ (22)

其中 $G_1=2\times rand-1$ ， $G_2=1-t/T$ ，分别用以跟踪最优解运动与表现2到0的递减值。表示用于均衡策略的质量函数，可表示为：

$QF\left(t\right)=t^{\frac{2\times rand-1}{{\left(1-T\right)}^2}}$ (23)

4. 实验

4.1. 实验准备

为了验证本文所提出控制算法的有效性，包括轨迹跟踪性能与抵抗外部未知干扰的能力，建立二自由度下肢外骨骼实验平台，平台由三部分组成：1) 上位机控制部分：控制方法在Matlab/Simulink中编程并编译，加载到Labview中观察相应控制效果；2) 信号采集部分：由安装在髋关节与膝关节的两个绝对编码器与数据采集卡测量运动步态数据；3) 下肢外骨骼执行部分：由安装在外骨骼上的两个直流电机与模拟量输出卡组成，以驱动二自由度下肢外骨骼原型并实现所需的运动。

实验平台结构如图5所示。

为了验证本文使用的SMC方法与Aquila优化器的有效性，应用不同的控制方法(PID、SMC、GA-SMC与AO-SMC)观察控制效果，比较步态跟踪精度的区别。

对于PID控制器，比例系数为1.2、积分系数为31、微分系数为0.4，PID控制下的跟踪曲线如图6所示。在传统SMC控制器中，开关增益系数为300，轨迹跟踪效果如图7所示。对于GA-PID控制器，种群数量设置为100，迭代次数为50，变异概率与交叉概率设置分别为0.2与0.1，步态跟踪精度如图8所示。对于AO-AMC控制器，参数选取与文献 [17] 中相同，轨迹跟踪结果如图9所示。

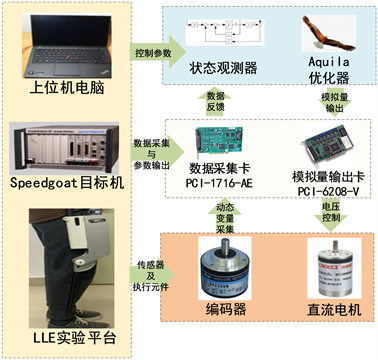
Figure 5. Lower extremity exoskeleton experimental platform

图5. 下肢外骨骼实验平台

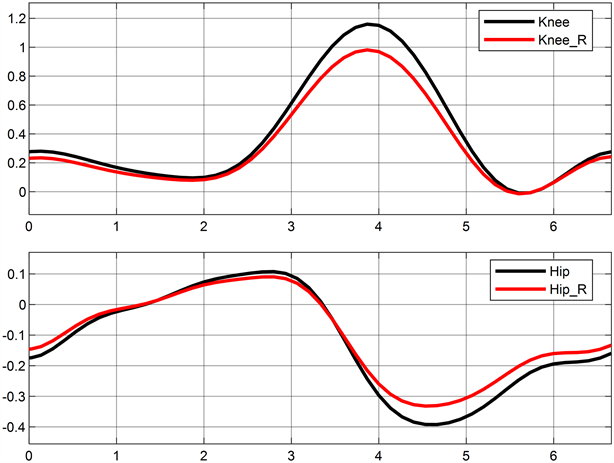
Figure 6. PID joint trajectory tracking diagram

图6. PID关节轨迹跟踪图

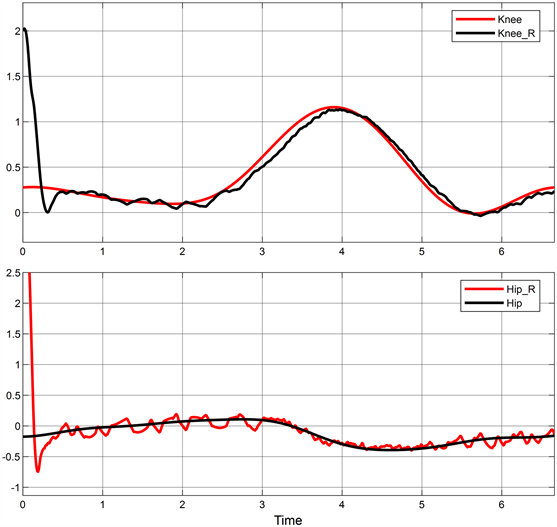
Figure 7. SMC joint trajectory tracking diagram

图7. SMC关节轨迹跟踪图

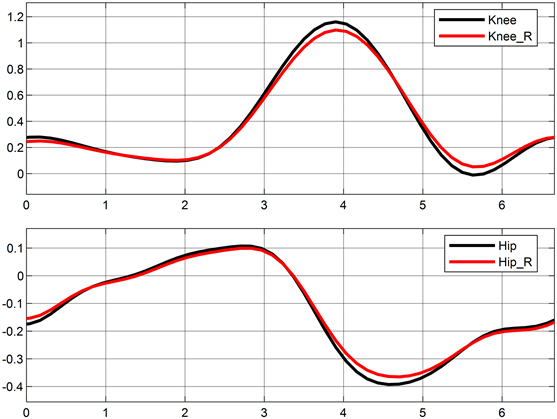
Figure 8. GA-SMC joint trajectory tracking diagram

图8. GA-SMC关节轨迹跟踪图

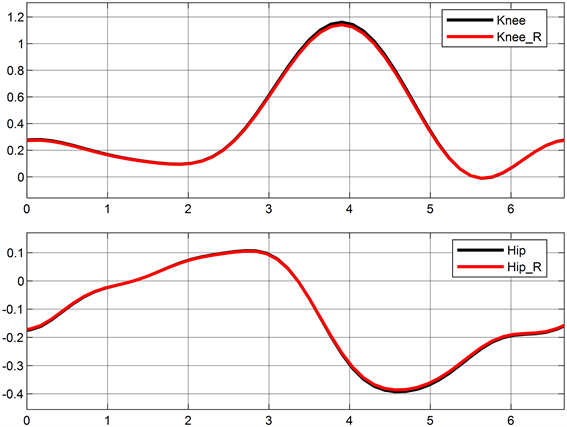
Figure 9. AO-SMC joint trajectory tracking diagram

图9. AO-SMC关节轨迹跟踪图

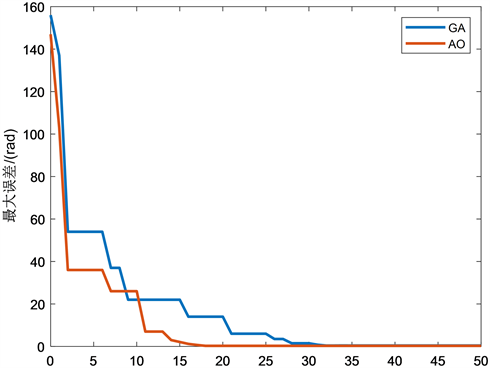
Figure 10. Comparison of iterative algebra and tracking accuracy between GA and Aquila optimizer

图10. GA与Aquila优化器迭代代数与跟踪精度对比

图6中，PID控制方法下的最大跟踪误差约为1.3 rad，约为图7中SMC方法误差的2.4倍，可知SMC方法拥有更稳定的跟踪精度，对此类非线性问题具有更好的控制效果。图8与图9分别使用遗传算法优化器(GA)与Aquila优化器进一步提高控制器的跟踪精度，最大跟踪误差分别为0.41 rad与0.28 rad，分别是传统SMC方法的31%与22%。其迭代过程如图10所示，由图10可知两者分别在第32与第19次迭代过程中得到最优参数。实验表明，Aquila优化器具有更快的参数寻优速度，Aquila优化器可使控制器有更好的轨迹跟踪控制效果。

4.3. NDO抗干扰能力评估

为考察NDO的抗干扰能力，将SMC方法与NDO-SMC方法比较，观察两者在引入干扰信号情况下的跟踪精度。实验中SMC控制器的参数保持不变。两者的跟踪精度比较如图11与图12所示。

对比图7与图11可观察到，图11中最大跟踪误差为2.34 rad，是无干扰时的1.4倍，说明干扰信号对控制器跟踪精度有较大影响。对比图11与图12可以观察到，图12中NDO-SMC的步态轨迹跟踪最大误差为1.73 N，跟踪精度相比较SMC方法的轨迹跟踪精度提升了31%。由此得到结论，NDO可检测到干扰误差并作出相应的补偿干扰，带有NDO的控制器具有更好的抗干扰能力。

4.4. AO-SMC方法的性能评估

为验证AO-SMC在干扰环境下的轨迹跟踪效果，分别比较SMC与AO-SMC控制器的轨迹跟踪误差。同时观察不同控制方法下的控制信号振幅，以比较不同控制方法的控制信号稳定性。AO-SMC方法迭代出的控制参数数值如表3所示。

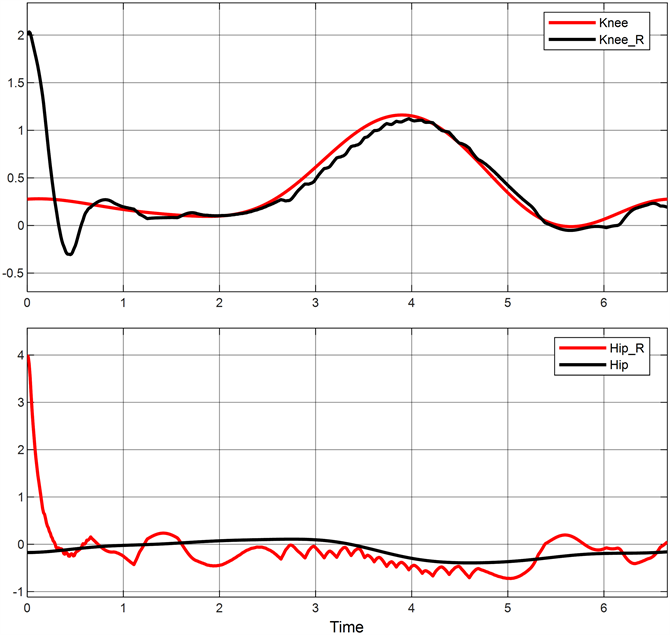
Figure 11. SMC joint trajectory tracking diagram with interference

图11. 带有干扰的SMC关节轨迹跟踪图

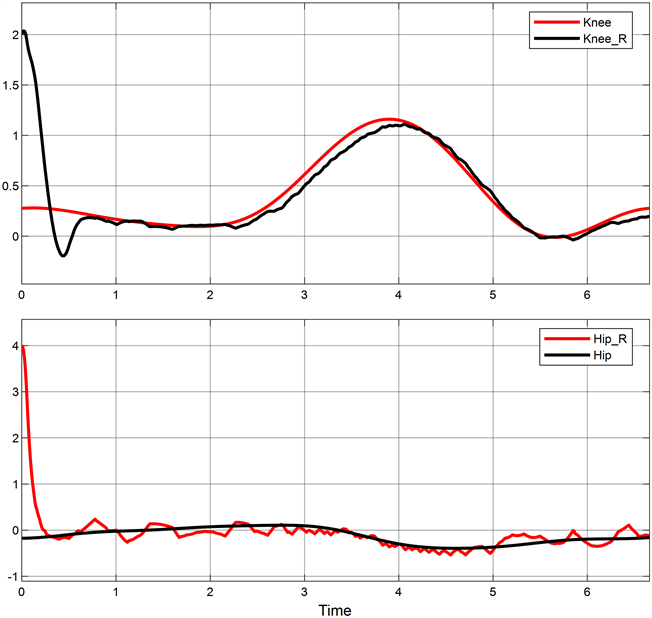
Figure 12. NDO-SMC joint trajectory tracking diagram with interference

图12. 带有干扰的NDO-SMC关节轨迹跟踪图

Table 3. AO-SMC control parameters

表3. AO-SMC控制参数

两种控制方法的曲线跟踪效果与控制信号振幅比较如图12与图13所示。

比较图13中SMC方法与AO-SMC方法的最大跟踪误差可得：AO-SMC方法最大跟踪误差约为0.21 rad，优化后的步态精度提高了63%，表明AO-SMC方法有更好的轨迹跟踪精度。同时从图14中可以观察到AO-SMC的控制信号振动幅度更小，约为SMC方法的21%，表明使用AO-SMC方法有更好的控制信号稳定性，对控制信号振动幅度有较好的抑制作用。

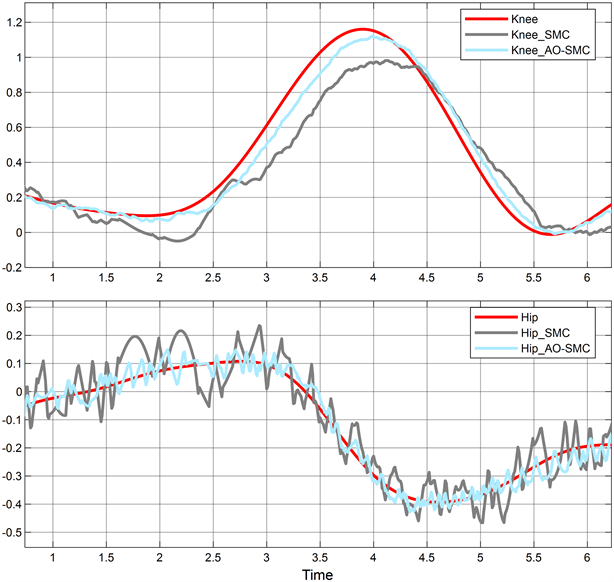
Figure 13. Comparison of SMC and AO-SMC trajectory tracking

图13. SMC与AO-SMC轨迹跟踪比较

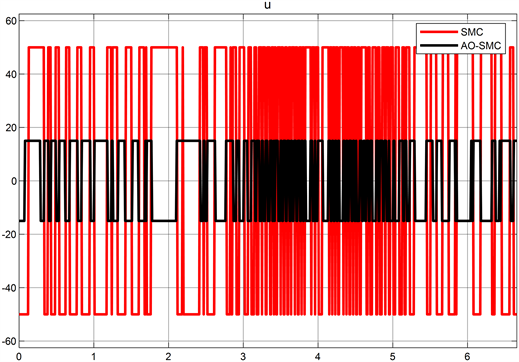
Figure 14. Comparison of amplitudes of SMC and AO-SMC control signals

图14. SMC与AO-SMC控制信号振幅比较

5. 结束语

本文以双关节下肢助力外骨骼作为研究对象，设计了一种结合非线性观测器的滑模控制方法，并验证该方法有效性。实验表明，改进的优化器有较好的寻优能力，带有NDO的控制器具有更好的抗干扰能力，对比传统SMC方法与本文AO-SMC方法的控制效果，AO-SMC方法的步态跟踪精度提升了63%。后续研究考虑在外骨骼中增加IMU等其他传感器以进一步提高步态精确性。