瞬态非牛顿流体非定常流动问题的等几何分析

Isometric Analysis of Unsteady Flow of Tran-sient Non-Newtonian Fluids

摘要: 非牛顿流体非定常流动问题是指流动过程中流体的物理性质随时间变化的复杂流动问题，为了改进传统分析方法在处理复杂流动问题上精度及效率不足的缺陷。本文从经典N-S方程入手，推导出了一种高效等几何求解方法，通过选择合适的等效流动参数，确定等价定常流动条件，将复杂非定常问题转化为一组等价的定常流动问题。最后以平板拖曳模型为例，得到了各时刻流体的速度分布，并与商业分析软件进行对比，通过不同的迭代步长的计算精度，来验证该方法的计算效率。该方法能帮助工程人员更好地理解流体的流动特性，为设计优化工艺过程和提高机器设备的效率提供重要的理论依据。

Abstract: Non-newtonian fluid unsteady flow problem refers to the complex flow problem in which the physi-cal properties of the fluid change with time. In order to improve the defect of the traditional analy-sis method in dealing with the complex flow problem, the accuracy and efficiency are insufficient. Based on the classical N-S equation, an efficient isogeometric solution method is derived. By select-ing appropriate equivalent flow parameters and determining equivalent steady flow conditions, complex unsteady problems are transformed into a set of equivalent steady flow problems. Finally, the fluid velocity distribution at each moment is obtained by taking the flat plate towing model as an example, and compared with commercial analysis software, the computational efficiency of the proposed method is verified by calculating accuracy of different iteration steps. This method can help engineers better understand the flow characteristics of the fluid and provide important theo-retical basis for optimizing the design process and improving the efficiency of machinery and equipment.

1. 引言

流体等几何分析是一种处理复杂流动问题的计算机辅助图形学方法，用于研究各类流体在不同条件下的流动特性。它通常用于探究物理参数随时间和空间的变化特性，从而增强工程人员对流体运动的理解。等几何流体分析可以用来研究流体的压强、速度场和能量守恒等物理量，并且可以用来模拟流体在不同流动状态下的行为。这种方法通常用于流体力学领域，并广泛应用于工业、航空、航天和水利等领域 [1]。

在流体工业中，等几何分析的优势在于它可以帮助研究人员更好地理解流体的流动特性，从而更好地设计工艺过程和机器设备 [2]。等几何分析可以帮助研究人员预测流体在不同压力、温度和流速条件下的流动行为。例如，可以分析流体与固体物体的相互作用，比如流体经过一个闸门时产生的水力压力，或者流体与桨叶等旋转物体相互作用时产生的流动特态 [3]。

此外，还可以分析流体在管道、容器或其他机械设备中的流动情况，捕捉流体中的湍流现象 [4]。由于等几何分析的天然优势，使其可高效地探究不同的设计参数对流体流动的影响 [5]。这些信息对于优化工艺过程、提高机器设备的效率和降低能耗都非常重要。

本文将等几何分析方法引入非牛顿流体非定常流动问题中进行求解，并结合平板拖曳模型对该方法进行了验证及误差分析，验证了该方法既能简化非定常的计算也能有比较高的计算精度，为流体仿真工业计算提供了帮助。

2. 等几何分析的基本思想

等几何分析方法拥有着其独特的内在核心思想，其体参数化建模几何基函数和仿真分析的形函数采用同样的网格模型，能实现具有高准确性几何模型的仿真分析。以二维问题的平面表示方法为例，NURBS(非均匀有理B样条)曲面表示的样条空间可以通过以下公式定义 [6]：

$S\left(\xi ,\eta \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{N}_{i,j}^{p,q}\left(\xi ,\eta \right)P_{i,j}}}$ (1)

其中 $\xi$ 和 $\eta$ 为样条参数， $P_{i,j}$ 为控制点，双变量的NURBS基函数表达式为

$N_{i,j}^{p,q}\left(\xi ,\eta \right)=\frac{B_{i,p}\left(\xi \right)B_{j,q}\left(\eta \right){\omega }_{i,j}}{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{\displaystyle \underset{j=1}{\overset{m}{\sum }}{B}_{i,p}\left(\xi \right)B_{j,q}\left(\eta \right){\omega }_{i,j}}}}$ (2)

式中 $B_{i,p}\left(\xi \right)$ 和 $B_{j,q}\left(\xi \right)$ 为单变量的B样条的样条基，阶次分别为p和q， ${\omega }_{i,j}$ 为特征点 $P_{i,j}$ 对应的权重。以某一单元为研究对象，设此单元的基函数节点向量为 $N=\left(N_1,N_2,\cdots ,N_L\right)$，则该单元的几何场的插值形式如下：

$X_e\left(\xi ,\eta \right)=P_e^{\text{T}}N={\left[x\left(\xi ,\eta \right)y\left(\xi ,\eta \right)\right]}^{\text{T}}$ (3)

其中，

$P_e=\left[\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\\ ⋮& ⋮\\ x_L& y_L\end{array}\right]$ (4)

3. 非牛顿流体非定常流动等几何分析方法理论

3.1. 数学方程

不考虑外度温度交换且忽略惯性项影响的非定常N-S方程组可表示为以下形式：

连续性方程:

$\frac{\partial u}{\partial x}+\frac{\partial v}{\partial y}=0$ (5)

x向运动方程：

$\rho \frac{\partial u}{\partial t}+\frac{\partial p}{\partial x}-\left(\frac{\partial {\tau }_{xx}}{\partial x,y}+\frac{\partial {\tau }_{xy}}{\partial y}\right)=0$ (6)

y向运动方程：

$\rho \frac{\partial v}{\partial t}+\frac{\partial p}{\partial y}-\left(\frac{\partial {\tau }_{yx}}{\partial x}+\frac{\partial {\tau }_{yy}}{\partial y}\right)=0$ (7)

式中，p为流体密度，切应力 $\tau$ 的计算式为：

$\tau =\left(\begin{array}{ll}{\tau }_{xx}\hfill & {\tau }_{xy}\hfill \\ {\tau }_{yx}\hfill & {\tau }_y\hfill \end{array}\right)=\mu \left(\begin{array}{cc}2\frac{\partial u}{\partial x}& \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\\ \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}& 2\frac{\partial v}{\partial y}\end{array}\right)$ (8)

代入上式得到：

$\rho \frac{\partial u}{\partial t}+\frac{\partial p}{\partial x}-\mu \left[2\frac{\partial }{\partial x}\left(\frac{\partial u}{\partial x}\right)+\frac{\partial }{\partial y}\left(\frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\right)\right]=0$ (9)

$\rho \frac{\partial v}{\partial t}+\frac{\partial p}{\partial y}-\mu \left[\frac{\partial }{\partial x}\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)+2\frac{\partial }{\partial y}\left(\frac{\partial v}{\partial y}\right)\right]=0$ (10)

3.2. 边界条件

流体等几何分析中常用的物理边界条件主要有以下几种 [7]，包括：

流入、流出边界：它表征了系统在流体或颗粒流进入流域的边界处的物理表现，常常以出入口的速度为边界值，直接影响速度参数，在流体工业中特别的重要。

壁边界条件：指定固体边界的条件(例如无滑移或滑移条件)。固体壁边界条件设定了流体与壁面相互接触时的状态，或是被壁面反射或吸收等一系列状态量。

压力边界条件：直接施加在力项中，阐述了流体受到各种外界力学状态变化(例如大气压力或水泵施加的压力)的力学边界上的行为。

一般来说，等几何流体分析中，边界条件的选取，需要考虑问题的具体表现，以及该问题解决方案的准确性要求。为了从仿真计算中获得精确且高效的结果，根据实际情况选择正确的边界条件十分重要。本文流体边界条件是设置在壁面无滑移假设的情况下，即本文研究问题的速度边界条件为：

${u|}_{\Gamma }=\hat{u},\hat{p}=0,{v|}_{\Gamma }=\hat{v}$ (11)

3.3. 运动方程的单元方程

在等几何分析网格搭建计算过程中，需要在三个域中进行参数转换，它们分别是物理域 $\Omega$ 和它的子域 ${\Omega }_e$，参数域 $\hat{\Omega }$ 和它的子域 ${\hat{\Omega }}_e$ 以及母域 $\tilde{\Omega }$ 和它的子域 ${\tilde{\Omega }}_{\text{e}}$。它们之间的含有如下文所示的映射关系，母域到参数子域的映射可表示为： ${\tilde{\varphi }}_e:\tilde{\Omega }\to {\hat{\Omega }}_e$，从参数子域映射到物理子域的映射可表示为 $S:{\hat{\Omega }}_e\to {\Omega }_e$。对于2D平面情况，参数空间中的元素为 ${\hat{\Omega }}_e=\left[{\xi }_i,{\xi }_{i+1}\right]\otimes \left[{\eta }_j,{\eta }_{j+1}\right]$ 参数空间中的任意一点 $\left(\xi ,\eta \right)$ 都可以通过映射 ${\tilde{\varphi }}_e:\tilde{\Omega }\to {\hat{\Omega }}_e$ 用点 $\left(\tilde{\xi },\tilde{\eta }\right)$ 来表示 [7]。

$\left[\begin{array}{c}\xi \\ \eta \end{array}\right]={\tilde{\varphi }}^e\left(\xi \right)=0.5\left[\begin{array}{c}\left({\xi }_{i+1}-{\xi }_i\right)\tilde{\xi }+\left({\xi }_{i+1}+{\xi }_i\right)\\ \left({\eta }_{j+1}-{\eta }_j\right)\tilde{\eta }+\left({\eta }_{j+1}+{\eta }_j\right)\end{array}\right]$ (12)

映射 $S:{\hat{\Omega }}_e\to {\Omega }_e$ 的雅可比变换矩阵为

$J_1=\left[\begin{array}{cc}\frac{\partial x}{\partial \xi }& \frac{\partial x}{\partial \eta }\\ \frac{\partial y}{\partial \xi }& \frac{\partial y}{\partial \eta }\end{array}\right]$ (13)

由参数坐标到母单位坐标变换的雅可比矩阵变换行列式为：

$J_2=\left[\begin{array}{cc}\frac{1}{2}\left({\xi }_{i+1}-{\xi }_i\right)& 0\\ 0& \frac{1}{2}\left({\eta }_{j+1}-{\eta }_j\right)\end{array}\right]$ (14)

$X_e:\tilde{\Omega }\to {\Omega }_e$ 映射的雅可比矩阵为

$J=J_1\ast J_2$ (15)

3.4. 多片模型体参数化空间的选定

在NURBS体参数化空间的造构过程中，我们应该合理选择离散空间，在参数域中，样条空间 $N_P\left(\zeta ,\eta \right)$ 用于定义几何的压力NURBS空间，对于速度空间，它的的次数和节点向量与NURBS几何体本身一致，但应增加次数 [8]。定义空间 $S_{p+1}\left(\zeta ,\eta \right)$，其中每个 $N_P\left(\zeta ,\eta \right)$ 与 $S_{p+1}\left(\zeta ,\eta \right)$ 具有相同的节点，但样条次数增加了1，不同的形函数交叠求解，可以避免流体仿真求解震荡 [8]，流体等几何分析方法积分过程原理图如下图1所示：

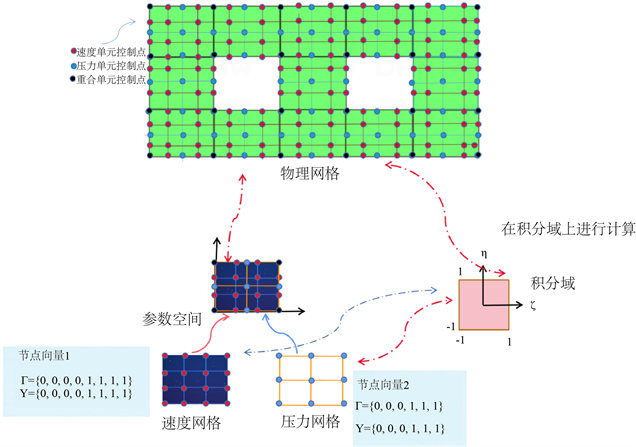
Figure 1. Integral process of isogeometric fluid analysis

图1. 流体等几何分析积分过程

物理域内某一点的速度、压力参数可以用以下节点数据与形函数的乘积代表：

$u_k\left(\xi ,\eta \right)={\displaystyle \underset{i=1}{\overset{n}{\sum }}{u}_{k,i}{S}_i\left(\xi ,\eta \right)}$ (16)

$p\left(\xi ,\eta \right)={\displaystyle \underset{j=1}{\overset{m}{\sum }}{u}_j{N}_j\left(\xi ,\eta \right)}$ (17)

将总体区域的参数通过积分变换转变到单元区域，并且将式(16)、式(17)代人到运动方程各项中。对于计算时间项，x和y方向的运动方程计算中，时间项可分别由以下形式表达：

${\displaystyle {\iint }_{\sigma }\Phi \rho \frac{\partial u}{\partial t}\left|J\right|\text{d}x\text{d}y}=\rho {\displaystyle {\iint }_{\sigma }\left|J\right|{\Phi }^{\text{T}}\text{d}x\text{d}y}\stackrel{\dot{}}{u}=M^e\stackrel{\dot{}}{u}$ (18)

${\displaystyle {\iint }_{\sigma }\Phi \rho \frac{\partial u}{\partial t}\left|J\right|\text{d}x\text{d}y}=\rho {\displaystyle {\iint }_{\sigma }\left|J\right|{\Phi }^{\text{T}}\text{d}x\text{d}y}\stackrel{\dot{}}{u}=M^e\stackrel{\dot{}}{v}$ (19)

式中，

$M^e=\rho {\displaystyle {\iint }_{\Omega }\left|J\right|\Phi {\Phi }^{\text{T}}\text{d}x\text{d}y}$ (20)

得到单元方程为：

$B{e}_{1}u+B{e}_{2}v=0$ (21)

$M^e\stackrel{\dot{}}{u}+D_{11}^e{u}_I^e+D_{12}^e{v}_I^e-C_1^e{p}_I^e=-F_1^e$ (22)

$M^e\stackrel{\dot{}}{v}+D_{21}^e{u}_I^e+D_{22}^e{v}_I^e-C_2^e{p}_I^e=-F_2^e$ (23)

式中，D子块的求解需要先得到结点黏度，黏度的推导满足幂律流体本构公式：

$\tau =\mu \stackrel{\dot{}}{\gamma }=m{\left|\stackrel{\dot{}}{\gamma }\right|}^{n-1}\stackrel{\dot{}}{\gamma }=m{\left|\sqrt{2\underset{\_}{\underset{\_}{D}}:\underset{\_}{\underset{\_}{D}}}\right|}^{n-1}\stackrel{\dot{}}{\gamma }$ (24)

式中，m是稠度，n为幂律指数，剪切速率 $\stackrel{\dot{}}{\gamma }$ 包含速度的导数，在流体等几何分析中剪切速率 $\stackrel{\dot{}}{\gamma }$ 可表示为：

$\stackrel{\dot{}}{\gamma }={\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}^2\right]}^{\frac{1}{2}}$ (25)

最终可以获得流体黏度的表达式：

$\mu =m{\left[2{\left(\frac{\partial u}{\partial x}\right)}^2+2{\left(\frac{\partial v}{\partial y}\right)}^2+{\left(\frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right)}^2\right]}^{\frac{n-1}{2}}$ (26)

3.5. 总体方程的组合

通过上述单元刚度矩阵的描述，可对等几何分析单元方程进行组合，可得到总体方程。因此流体三大运动方程可表述为以下形式：

连续性总体方程：

$B_{1}u+B_{2}v=0$ (27)

运动总体方程：

$M\stackrel{\dot{}}{u}+D_{11}u+D_{12}v-C_{1}p=-F_1$ (28)

$M\stackrel{\dot{}}{v}+D_{21}u+D_{22}v-C_{2}p=-F_2$ (29)

3.6. 非定常问题非线性方程组的求解方法

通过式(28)、(29)中可以看出， $\stackrel{\dot{}}{u}$ 、 $\stackrel{\dot{}}{v}$ 分别为速度u、v对时间的导数，即：

$\stackrel{\dot{}}{u}=\frac{u^{n+1}-u^n}{\text{Δ}t}$ (30)

$\stackrel{\dot{}}{v}=\frac{v^{n+1}-v^n}{\text{Δ}t}$ (31)

式中，n + 1和n代表相近两个时刻，n + 1表示当前时刻，n表示上一时刻。

此时，设置参数 $\theta$，将式(27)、(28)中的未知数u，v以及压力p表示为当前时刻(n + 1)和前一时刻n分布结果的加权解：

$u=\theta u_{n+1}+\left(1-\theta \right)u_n$ (32)

$v=\theta v_{n+1}+\left(1-\theta \right)v_n$ (33)

$p=\theta p_{n+1}+\left(1-\theta \right)p_n$ (34)

式中， $0\le \theta \le \text{1}$。将式(32)和式(33)、(34)分别代入式(27)、式(28)、式(29)，得到：

$\begin{array}{l}M{u}_{n+1}+\Delta t{D}_{11}\theta u_{n+1}+\Delta t{D}_{12}\theta v_{n+1}-\Delta t{C}_1\theta p_{n+1}\\ =M{u}_n-\Delta t{D}_{11}\left(1-\theta \right)u_n-\Delta t{D}_{12}\left(1-\theta \right)v_n+\Delta t{C}_1\left(1-\theta \right)p_n-\Delta t{F}_1\end{array}$ (35)

$\begin{array}{l}M{v}_{n+1}+\Delta t{D}_{21}\theta u_{n+1}+\Delta t{D}_{22}\theta v_{n+1}-\Delta t{C}_2\theta p_{n+1}\\ =M{v}_n-\Delta t{D}_{21}\left(1-\theta \right)u_n-\Delta t{D}_{22}\left(1-\theta \right)v_n+\Delta t{C}_2\left(1-\theta \right)p_n-\Delta t{F}_2\end{array}$ (36)

$B_1{u}_{n+1}+B_2{v}_{n+1}=0$ (37)

可获得总体方程的线性表达式为：

$Kx=b$ (38)

其中：

$K=\left(\begin{array}{ccc}M+\Delta t{D}_{11}& \Delta t{D}_{12}\theta & -\Delta t{C}_1\theta \\ \Delta t{D}_{21}\theta & M+\Delta t{D}_{22}\theta & -\Delta t{C}_2\theta \\ B_1& B_2& 0\end{array}\right)$ (39)

$x=\left(\begin{array}{c}{u}_{n+1}\\ v_{n+1}\\ p_{n+1}\end{array}\right)$ (40)

式中，

$b=\left(\begin{array}{c}M{u}_n-\Delta t{D}_{11}\left(1-\theta \right)u_n-\Delta t{D}_{12}\left(1-\theta \right)v_n+\Delta t{C}_1\left(1-\theta \right)p_n-\Delta t{F}_1\\ M{v}_n-\Delta t{D}_{21}\left(1-\theta \right)u_n-\Delta t{D}_{22}\left(1-\theta \right)v_n+\Delta t{C}_2\left(1-\theta \right)p_n-\Delta t{F}_2\\ 0\end{array}\right)$ (41)

3.7. 误差分析

在迭代分析过程中，当相近两次计算结果的绝对误差或相对误差小于所需精度要求时，判定为计算收敛，即当前(n + 1)时刻的迭代计算结束，转至后续步骤；否则，回到n时刻的计算迭代流程中重新计算。绝对和相对偏差的表达公式分别为：

$R_{1绝对}=\max \left\{\left|u_{n+1}^{k+1}-u_{n+1}^k\right|,\left|v_{n+1}^{k+1}-v_{n+1}^k\right|,\left|p_{n+1}^{k+1}-p_{n+1}^k\right|,\left|{\mu }_{n+1}^{k+1}-{\mu }_{n+1}^k\right|\right\}$ (42)

$R_{1相对}=\max \left\{\frac{\left|u_{n+1}^{k+1}-u_{n+1}^k\right|}{\left|u_{n+1}^k\right|},\frac{\left|v_{n+1}^k-v_{n+1}^k\right|}{\left|v_{n+1}^k\right|},\frac{\left|p_{n+1}^k-p_{n+1}^k\right|}{\left|p_{n+1}^k\right|},\frac{\left|{\mu }_{n+1}^{k+1}-{\mu }_{n+1}^k\right|}{\left|{\mu }_{n+1}^k\right|}\right\}$ (43)

在计算当前(n + 1)时刻与前一时刻(n)分布误差R₂时，如果合计计算用时小于时间上限，且 $R_2\le \epsilon$，则表明计算达到目的，停止计算；如果合计计算时间抵达时间上限，但是 $R_2>\epsilon$，则说明，等几何分析流场分布还未平稳，直到计算时间达到时间上限，停止计算，非定常等几何流动问题的绝对误差和相对误差分别表示为：

$R_{2绝对}=\max \left\{\left|u_{n+1}-u_n\right|,\left|v_{n+1}-v_n\right|,\left|p_{n+1}-p_n\right|,\left|{\mu }_{n+1}-{\mu }_n\right|\right\}$ (44)

$R_{2相对}=\max \left\{\frac{\left|u_{n+1}-u_n\right|}{\left|u_n\right|},\frac{\left|v_{n+1}-v_n\right|}{\left|v_n\right|},\frac{\left|p_{n+1}-p_n\right|}{\left|p_n\right|},\frac{\left|{\mu }_{n+1}-{\mu }_n\right|}{\left|{\mu }_n\right|}\right\}$ (45)

4. 求解实例

本节将利用等几何分析方法研究如图2所示区域内的非牛顿流体的非定常流动，流体黏度服从Bird-Carreau模型 [9]：

$\mu ={\mu }_{\infty }+\left({\mu }_0-{\mu }_{\infty }\right){\left(1+{\lambda }^2{\stackrel{\dot{}}{\gamma }}^2\right)}^{\frac{n-1}{2}}$ (46)

模型中各符号的含义见下表1，流体部分是一个50 cm × 40 cm的矩形区域，中间内嵌固体区域的尺寸为10 cm × 10 cm，上方有一固体平板，从左往右与域内流体发生接触运动，且板的移动速率在10 s内从0 m/s缓慢增加到1 m/s，随后十秒内速度由1 m/s缓缓减速到0。求解不考虑流动惯性项影响且与外界无能量交换。

Table 1. Partial physical property parameter

表1. 部分物性参数

Figure 2. Flatbed towed flow model

图2. 平板拖曳流动模型

结果分析

在开始等几何流体分析计算前，需要给定初始条件，设流域初始速度为零，流动迭代运算的时间步长间隔为1 s，进入迭代计算，最终得出流场各个时刻的速度分布，如下图3所示，前半部分(0 s~10 s)过程中，流场处于加速流动状态，后半部分(0 s~10 s)流场处于减速流动状态。

为了验证等几何流体分析方法的准确性，本文利用等几何分析方法并用Matlab生成的流域速度分布与成熟商业有限元软件Fluent得到的有限元分析结果相对比，以此来验证等几何分析方法的准确性，以1 s、5 s、10 s、15 s、20 s这几个时刻的分析结果为对照，得到前20 s的速度分布对比如下：

由上图可以看出，各个时刻的分析结果大体上分布一致，且T = 10 s时，等几何分析方法得出的最大流域速度为1.43 m/s，有限元分析软件得出的最大流速为1.35 m/s，两种分析方法在数值上接近，也验证了该方法的准确性。

需要重视的是，在T = 20 s时，流域的速度并未完全等于0 m/s的理论速度。实际上，如果将时间步长取得足够小(趋近于0)，流域前后两个时刻的速度应该互相独立。但是，实际程序实现过程中，由于迭代时间步长的影响，T = 20 s时，速度分布却不为零，实际的流域均速为4.27 × 10⁻⁴ m/s，直到T = 23 s时，流域平均速度才降至1.91 × 10⁻¹⁵ m/s。将迭代步长设置为0.5 s时，T = 20 s时流域平均流速变为2.13

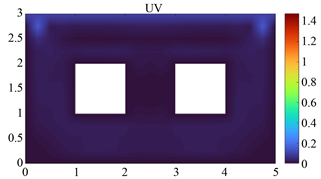
T = 1 s

T = 5 s

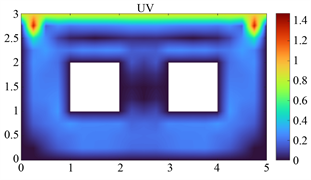
T = 10 s

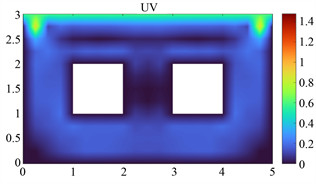
T = 15 s T = 20 s

Figure 3. Isogeometric analysis method (left) and commercial analysis software (right) instantaneous comparison of 0~20 s flow field velocity distribution

图3. 等几何分析方法(左)与商业分析软件(右) 0~20 s流场速度分布瞬时对比图

× 10⁻⁴ m/s，当T = 20.5 s时，区域流速达到6.83 × 10⁻¹⁷ m/s的收敛条件。综上所述，迭代计算时间间隔越小，两个时刻之间的影响就会越小。

为了验证不同迭代步长对程序计算精度的影响，在不考虑非牛顿流体的微小惯性的情况下，选取T = 20 s的时刻作为对比，此时流域速度的理论值应该为0 m/s，对不同时间步长1 s、0.5 s、0.1 s、0.01 s分别进行迭代计算，得到了如下表2所示的计算用时及精度对比表：

Table 2. Calculation time and precision under different time steps

表2. 不同时间步长下的计算用时及其精度

由上表可知，时间步长越短，达到收敛的时刻越早，计算结果越精确，但程序计算用时也同步增加，使用等几何分析方法的工程人员可根据精度、时间、便捷的选取合适的时间步长，提高流体仿真工业计算效率。

5. 总结与展望

本文以等几何分析方法为基础，将流体分析方法与体参数化模型相融合，并加以拓展，推导出非牛顿流体的等几何分析求解方法，讲述了非牛顿流体黏度的计算方法以及非牛顿流体问题求解的迭代方法。最后加入时间项，引入平板拖曳流模型，讲述瞬态非牛顿流体非定常流动的理论及其实例求解，并通过对比不同迭代步长分析其对计算精度的影响，证明了该方法在迭代步长足够小时间，能有较高的计算精度。

本文的模型是一个理论模型，后续可以对诸多实际问题展开研究，例如环境保护、能源利用、航天航空、船舶工业等领域。这些问题往往涉及到流体运动的复杂性和不确定性，需要使用更加精细的数学模型和计算方法来进行分析和预测 [10]。随着计算机技术的发展，流体等几何分析的计算机模拟和计算能力也会得到提升，为流体运动的分析和预测提供强大的工具，未来的流体等几何分析也会更加注重自动化和智能化，帮助工程人员提高工作效率。