非线性脉冲系统有限时间输入到状态稳定性研究

Study on Finite-Time Input-to-State Stability of Nonlinear Impulsive Systems

摘要: 基于李雅普诺夫理论，给出了在固定驻留时间条件下非线性脉冲系统有限时间输入到状态稳定(FTISS)的一个充分条件。在连续动力学部分和脉冲动力学部分均考虑了外部输入的情况下，对于不稳定的脉冲作用，给出了系统有限时间输入到状态稳定脉冲频率、系统结构和外部扰动之间的关系。并通过实例说明了该理论的正确性。

Abstract: Based on Lyapunov theory, a sufficient condition for finite-time input-to-state stability (FTISS) of nonlinear impulsive systems with fixed dwell time is given. In the case that the external input is considered in both the continuous dynamics part and the pulse dynamics part, the relationship between the finite-time input-to-state stability pulse frequency, the system structure and the ex-ternal disturbance is given for the unstable pulse action. A numerical example is provided to demonstrate the correctness of the theoretical results.

1. 引言

在科技领域和自然界物理现象的许多变化过程中，运动状态可能会在某一时刻发生突变，而这个时间可以看作是瞬间发生的，即以脉冲的形式出现。脉冲系统是一类特殊的混杂系统，由三部分构成：用微分方程描述连续动力学部分，控制系统在脉冲之间的运动；用差分方程描述离散动力学部分，控制瞬时状态跳跃或者脉冲瞬间的重置；以及脉冲频率，决定这些脉冲何时发生。在过去几十年，脉冲系统越来越受到学者的关注 [1] [2]。一般来说，脉冲系统问题可以分为两类，即脉冲控制问题 [3] [4] 和脉冲干扰问题 [5] [6] [7]，并在许多领域得到了广泛应用，如网络控制系统 [5]、生物模型 [6] 和多智能体控制 [7] 等。

稳定性理论的研究是非线性系统研究中经久不衰的一个课题。相较于传统的Lyapunov渐近稳定性，有限时间稳定性(FTS)在控制理论研究中具有广泛的应用价值，如高阶滑膜控制问题 [8] [9]。FTS不仅需要李雅普诺夫稳定性，而且需要有限时间的收敛性。近年来，不少学者对非线性系统FTS做了广泛的研究。例如，Bhat给出了连续非Lipschitz自治系统平衡点FTS [10]，Polyakov提出两种非线性控制算法给出了闭环系统的全局有限时间稳定性 [11]，Lu利用Lyapunov的反函数提供了有限时间收敛的充分条件 [12]。对于非线性脉冲系统的有限时间稳定性，文献 [13] 建立了非线性系统分别在具有镇定效应的脉冲和脉冲扰动作用下FTS的李雅普诺夫定理，并提供了估计关于脉冲时间序列的沉降时间的充分条件。文献 [14] 研究了非线性脉冲系统的有限时间稳定性和固定时间稳定性，并得到了更为一般的李雅普诺夫定理。在输入系统中，输入到状态稳定(ISS)描述了外部输入对系统稳定性的影响，除了作为分析工具之外，在非线性控制系统的设计中具有核心作用，使其在过去几年也引起了许多关注。例如，Cai研究了基本预测器反馈的逆最优性和干扰衰减性质 [15] 以及加性对象扰动ISS [16]，Dashkovskiy证明非线性脉冲系统在满足广义平均驻留时间条件的序列ISS [17]。文献 [18] 中首次引入了FTISS，并提出了非线性系统FTISS的几个充分条件和必要条件。到目前为止，由于非线性系统的非光滑性有关的技术难度和复杂性，即使是在线性系统中对FTISS的研究也很少 [19] [20]。最近，文献 [21] 利用李雅普诺夫理论和驻留时间法给出了非线性脉冲系统FTISS的充分条件，具体地说，存在具有局部Lipschitz连续函数 $V:{ℝ}^n\to {ℝ}_{+}$ 使得

$D^{+}V\left(x\left(t\right)\right)\le -c{V}^{\alpha }\left(x\left(t\right)\right)$，当 $V\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$，

其中 $c>0$， $\alpha \in \left(0,1\right)$， $\omega$ 为外部输入。然而，在很多实际应用中，对上式李雅普诺夫函数的导数有以下形式：

$D^{+}V\left(x\left(t\right)\right)\le -c{V}^{\alpha }\left(x\left(t\right)\right)-qV\left(x\left(t\right)\right)$，当 $V\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$，

其中 $q>0$。如果直接将后面的 $-qV\left(x\left(t\right)\right)$ 用0替代，则我们在估计的收敛时间时会出现较大的误差。受上述思想的启发，本文将改进推广文献 [21] 中的结论，并给出了更一般的非线性脉冲系统FTISS的充分条件。

2. 预备知识

令 $ℝ$ 为实数集； ${ℝ}_{+}$ 为非负实数集； $\mathbb{N}$ 为正整数集； ${\mathbb{Z}}_0$ 为非负整数集； ${ℝ}^n$ 为n维欧氏空间； $\left|\cdot \right|$ 为二维欧氏范数； $a\vee b$ 和 $a\wedge b$ 分别为a和b的最大值和最小值；对于 $I\subseteq ℝ$， $m\ge 1$，令 $\omega :I\to {ℝ}^m$ 是一个可测的基本有界函数且为最大范数，特别地 ${\Vert \omega \Vert }_{\infty }:={\Vert \omega \Vert }_{\left[0,\infty \right)}$，对于 $\rho >0$，。

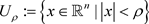考虑一个非线性脉冲系统

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=f\left(x\left(t\right),\omega \left(t\right)\right),t=t_k,\\ x\left(t\right)=g\left(x\left(t^{-}\right),\omega \left(t^{-}\right)\right),t\ne t_k,\\ x\left(0\right)=x_0,\end{array}$ (1)

这里 $x\left(t\right)\in {ℝ}^n$ 为系统状态； $x_0\in {ℝ}^n$ 是一个已知的初始状态； $\omega \left(t\right)\in {ℝ}^m$ 是一个可测的基本有界的外部输入； $f:{ℝ}^n\times {ℝ}^m\to {ℝ}^n$ 和 $g:{ℝ}^n\times {ℝ}^m\to {ℝ}^n$ 是满足 $f\left(0,0\right)=g\left(0,0\right)=0$ 的连续函数；脉冲时间序列 ${\left\{t_k\right\}}_{k\in \mathbb{N}}$ 满足 $0:=t_0<t_1<\cdots <t_k<\cdots$ 且 ${\lim }_{k\to +\infty }{t}_k=+\infty$ ；假设函数f满足适当的条件使得解 $x\left(t\right)=x\left(t,x_0\right)$ 在相关时间间隔内存在唯一正向解；假设 $x\left(t\right)$ 和 $\omega \left(t\right)$ 是左连续；对于给出的脉冲时间序列 $\left\{t_k\right\}$， $N\left(t,s\right)$ 表示系统(1)在半开区间 $(s,t]$ 上的脉冲次数。

对于一个局部Lipschitz连续函数 $V:{ℝ}^n\to {ℝ}_{+}$，沿着系统(1)的解 $x\left(t\right)$ 的右上导数定义为

$D^{+}V{\left[x\left(t\right)\right]}_f=\lim {\sup }_{h\to 0^{+}}\frac{1}{h}\left(V\left(x\left(t\right)+hf\left(x\left(t\right),\omega \left(t\right)\right)\right)-V\left(x\left(t\right)\right)\right)$.

定义1.1：如果函数 $\gamma :{ℝ}_{+}\to {ℝ}_{+}$ 是连续的，严格递增并且 $\gamma \left(0\right)=0$，则称函数 $\gamma$ 是 $\mathcal{K}$ 类函数。如果函数 $\gamma \in \mathcal{K}$ 也是无界的，则称函数 $\gamma$ 是 ${\mathcal{K}}_{\infty }$ 类函数。

定义1.2：如果函数 $\beta :{ℝ}_{+}\times {ℝ}_{+}\to {ℝ}_{+}$ 满足：

i) 对每一个固定 $t\ge 0$， $\beta \left(\cdot ,t\right)$ 关于第一个变量是 $\mathcal{K}$ 类函数；

ii) 对于每一个固定 $s\ge 0$，且当 $t\to \infty$ 时， $\beta \left(s,t\right)$ 递减趋于0；

则称 $\beta$ 是 $\mathcal{K}\mathcal{L}$ 类函数。

定义1.3 [21]：如果函数 $\beta :{ℝ}_{+}\times {ℝ}_{+}\to {ℝ}_{+}$ 满足：

i) 对于每一个固定 $s\ge 0$，存在 $T\left(s\right)<\infty$，使得当 $t\to T\left(s\right)$ 时， $\beta \left(s,t\right)$ 递减趋于0；

ii) $\beta \left(0,0\right)=0$ ；

iii) 对于每一个固定 $t\ge 0$ 有

$\{\begin{array}{l}\beta \left(s_1,t\right)>\beta \left(s_2,t\right),\text{if}\beta \left(s_1,t\right)>0,s_1>s_2,\\ \beta \left(s_1,t\right)=\beta \left(s_2,t\right),\text{if}\beta \left(s_1,t\right)=0,s_1>s_2,\end{array}$

则称函数 $\beta :{ℝ}_{+}\times {ℝ}_{+}\to {ℝ}_{+}$ 是 $\mathcal{K}{\mathcal{L}}_0$ 类函数。

定义1.4：设 $U\subseteq {ℝ}^n$ 是一个包含原点的开集，如果存在 $\beta \in \mathcal{K}{\mathcal{L}}_0$， $\gamma \in {\mathcal{K}}_{\infty }$ 使得对任意 $x_0\in U$ 和 $\omega \left(t\right)\in {ℝ}^m$，系统(1)的解 $x\left(t,x_0\right)$ 满足

$\left|x\left(t,x_0\right)\right|\le \beta \left(\left|x_0\right|,t\right)+\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$，对 $\forall t\ge 0$， (2)

则系统(1)是FTISS。

与传统的ISS相比，FTISS的主要区别在于对于给定的初始状态 $x_0\in {ℝ}^n$， $x\left(t,x_0\right)$ 将在有限时间内进入最终界限，并且此后不超过这个界限。

假设 $\mathcal{F}$ 表示一类可容许的脉冲时间序列， ${\mathcal{F}}_{\tau }$ 表示一类满足固定驻留时间(FDT)条件的脉冲时间序列，即 ${\inf }_{k\in {\mathbb{Z}}_0}\left\{t_{k+1}-t_k\right\}\ge \tau$， $\forall \left\{t_k\right\}\in {\mathcal{F}}_{\tau }$。

3. 主要结果

下面，利用FDT条件建立非线性脉冲系统(1)的FTISS的充分条件。

定理2.1：假设 $V:{ℝ}^n\to {ℝ}_{+}$ 是一个局部Lipschitz连续函数，如果存在函数 ${\phi }_1,{\phi }_2,\chi \in {\mathcal{K}}_{\infty }$，常数 $c>0$， $\alpha \in \left(0,1\right)$， $q>0$， $\eta >1$， $\vartheta >0$，使得：

(A₁) ${\phi }_1\left(\left|x\right|\right)\le V\left(x\right)\le {\phi }_2\left(\left|x\right|\right)$， $x\in {ℝ}^n$ ；

(A₂) $V\left(g\left(x,\omega \right)\right)\le \eta V\left(x\right)+\chi \left(\left|\omega \right|\right)$， $x\in {ℝ}^n$， $\omega \in {ℝ}^m$ ；

(A₃) 当 $V\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 时：

$D^{+}V{\left[x\left(t\right)\right]}_f\le -c{V}^{\alpha }\left(x\left(t\right)\right)-qV\left(x\left(t\right)\right)$， $t\ne t_k$， (3)

其中 $x\left(t\right)$ 为系统(1)初值为 $x\left(0\right)=x_0$ 的解，这里 $x_0\in U_{\vartheta }$ ；

(A₄) $\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\tau }\right)>\left({\text{e}}^{-q\left(1-\alpha \right)\tau }-\frac{1}{{\left(2\eta \right)}^{1-\alpha }}\right){\mu }^{1-\alpha }\left(\vartheta \right)$，

这里 $\mu \left(\vartheta \right):=\left(2\eta \chi \left({\Vert \omega \Vert }_{\infty }\right)\right)\vee {\phi }_2\left(\vartheta \right)$，则系统(1)在 ${\mathcal{F}}_{\tau }$ 上是FTISS。

证明：对于任意满足条件(A₄)的 $\tau >0$，可以找到一个充分小的常数 $\delta >0$ 使得

$\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\tau }\right)\ge \left({\text{e}}^{-q\left(1-\alpha \right)\tau }-\frac{1}{{\left(2\eta \right)}^{1-\alpha }}\right){\mu }^{1-\alpha }\left(\vartheta \right)+\delta$ 且 $q\left(1-\alpha \right)\tau \ge \delta$。 (4)

因为 $\eta >1$，所以对任意 $\lambda \in \left[\frac{2{\eta }^2}{2\eta -1},2\eta \right]$，有 $\lambda >\eta$ 且 $\frac{\lambda }{\lambda -\eta }\le 2\eta$。令 $\rho :=1\wedge \left(\lambda -\eta \right)$，当 $\lambda -\eta <1$ 时， $\frac{1}{\rho }=\frac{1}{\lambda -\eta }<\frac{\lambda }{\lambda -\eta }=\frac{\lambda }{\rho }\le 2\eta$ ；当 $\lambda -\eta \ge 1$ 时， $\frac{1}{\lambda -\eta }\le \frac{1}{\rho }=1<\frac{\lambda }{\rho }=\lambda \le 2\eta$。因此，我们有

$\frac{1}{\rho }<\frac{\lambda }{\rho }\le 2\eta$。 (5)

令 $\left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 为任意脉冲时间序列。假设 $x\left(t\right)=x\left(t,x_0\right)$ 是系统(1)以 $x\left(0\right)=x_0$ 为初值的解，这里 $x_0\in U_{\vartheta }$。为了方便，我们令 $\nu \left(t\right):=V\left(x\left(t\right)\right)$。对于任意 $s\ge 0$，定义：

${\beta }_1\left(s,t\right):={\mu }^{1-\alpha }\left(s\right)-{\displaystyle {\sum }_{i=0}^{k-1}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_k}{t_{k+1}-t_k}}\right)$,

这里 $t\in \left[t_k,t_{k+1}\right)$ 且 $k\in {\mathbb{Z}}_0$。定义

${\beta }_2\left(s,t\right):=\{\begin{array}{l}{\beta }_1^{\frac{1}{1-\alpha }}\left(s,t\right),t\in \left[0,T\left(s\right)\right),\\ 0,t\ge T\left(s\right),\end{array}$

这里 $T\left(s\right):=\inf \left\{t\ge 0|{\beta }_1\left(s,t\right)\le 0\right\}$。下面证明

$\nu \left(t\right)\le {\beta }_2\left(\left|x_0\right|,t\right)\vee \left(2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)\right)$, 对 $\forall t\ge 0$。 (6)

因为 $x\left(t\right)$ 和 $\omega \left(t\right)$ 在脉冲点上右连续，所以存在一个时间序列 $0:=t_0^{\vee }\le t_1^{\wedge }<t_1^{\vee }<t_2^{\wedge }<t_2^{\vee }<\cdots$ 使得对于 $l\in {\mathbb{Z}}_0$ 有

$\rho \nu \left(t\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$， $\forall t\in \left[t_{l-1}^{\vee },t_l^{\wedge }\right)$， (7a)

$\rho \nu \left(t\right)\le \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$， $\forall t\in \left[t_l^{\wedge },t_l^{\vee }\right)$。 (7b)

定义在区间 $\left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ 上的脉冲点为 $t_{{\xi }_l+1},\cdots ,t_{{\xi }_l+N\left(t_l^{\wedge },t_{l-1}^{\vee }\right)}$，这里 ${\xi }_l=N\left(t_{l-1}^{\vee },t_0^{\vee }\right)$。

首先引入变量变换 $Z\left(t\right)={\nu }^{1-\alpha }\left(t\right)$，则(3)式变为 $D^{+}Z\left(t\right)\le -c\left(1-\alpha \right)-q\left(1-\alpha \right)Z\left(t\right)$，由常数变易公式和比较原理得

$Z\left(t\right)\le {\text{e}}^{-q\left(1-\alpha \right)\left(t-t_k\right)}\left({\displaystyle {\int }_{t_k}^t-c\left(1-\alpha \right){\text{e}}^{q\left(1-\alpha \right)\left(s-t_k\right)}\text{d}s}+Z\left(t_k\right)\right)$， $t\in \left[t_k,t_{k+1}\right)$。

故

${\nu }^{1-\alpha }\left(t\right)\le {\text{e}}^{-q\left(1-\alpha \right)\left(t-t_k\right)}{\nu }^{1-\alpha }\left(t_k\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t-t_k\right)}\right)$. (8)

下面我们分两种情况考虑：情况(i) $t_1^{\wedge }>0$，即 $\left[0,t_1^{\wedge }\right)\ne \varnothing$ ；情况(ii) $t_1^{\wedge }=0$，即 $\left[0,t_1^{\wedge }\right)=\varnothing$。若情况(i)成立，对于 $\forall t\in \left[0,t_1^{\wedge }\right)$，当 $N\left(t_1^{\wedge },0\right)=0$ 时，即在区间 $\left[0,t_1^{\wedge }\right)$ 上没有脉冲，由(A₁)、(4)和(8)得

$\begin{array}{c}{\nu }^{1-\alpha }\left(t\right)\le {\text{e}}^{-q\left(1-\alpha \right)t}{\nu }^{1-\alpha }\left(x_0\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)t}\right)\le {\text{e}}^{-q\left(1-\alpha \right)t}{\nu }^{1-\alpha }\left(x_0\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\tau \frac{t}{t_1}}\right)\\ \le {\text{e}}^{-q\left(1-\alpha \right)t}{\nu }^{1-\alpha }\left(x_0\right)-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t}{t_1}}\right)\le {\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t}{t_1}}\right).\end{array}$ (9)

当 $N\left(t_1^{\wedge },0\right)>0$ 时，在区间 $\left[0,t_1^{\wedge }\right)$ 上的脉冲点为 $t_{{\xi }_1+i}=t_i$， $i\in \left\{1,\cdots ,N\left(t_1^{\wedge },0\right)\right\}$。所以由(9)得

${\nu }^{1-\alpha }\left(t\right)\le {\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t}{t_1}}\right)$， $t\in \left[0,t_1\right)$。

当 $t\in \left[t_1,t_2\wedge t_1^{\wedge }\right)$ 时，由(7a)可知， $\left(\lambda -\eta \right)\nu \left(t_1^{-}\right)\ge \rho \nu \left(t_1{}^{-}\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t_1\right)}\right)$。结合条件(A₂)，我们有

$\nu \left(t_1\right)\le \eta \nu \left(t_1^{-}\right)+\chi \left({\Vert \omega \Vert }_{\left[0,t_1\right)}\right)=\lambda \nu \left(t_1^{-}\right)-\left(\left(\lambda -\eta \right)\nu \left(t_1^{-}\right)-\chi \left({\Vert \omega \Vert }_{\left[0,t_1\right)}\right)\right)\le \lambda \nu \left(t_1^{-}\right).$

由(4)和(8)式得

$\begin{array}{c}{\nu }^{1-\alpha }\left(t_1\right)\le {\lambda }^{1-\alpha }{\nu }^{1-\alpha }\left(t_1^{-}\right)\\ \le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)t_1}{\nu }^{1-\alpha }\left(x_0\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)t_1}\right)\right)\\ \le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)\tau }{\nu }^{1-\alpha }\left(x_0\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\tau }\right)\right)\\ \le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)\tau }{\phi }_2^{1-\alpha }\left(\left|x_0\right|\right)-{\text{e}}^{-q\left(1-\alpha \right)\tau }{\mu }^{1-\alpha }\left(\left|x_0\right|\right)+\frac{1}{{\left(2\eta \right)}^{1-\alpha }}{\mu }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)\\ \le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-\delta .\end{array}$

继续将上式结果结合(4)和(8)式，对 $t\in \left(t_1,t_2\wedge t_1^{\wedge }\right)$ 我们有

${\nu }^{1-\alpha }\left(t\right)\le {\nu }^{1-\alpha }\left(t_1\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t-t_1\right)}\right)\le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_1}{t_2-t_1}}\right)$。

当 $t\in \left[t_2,t_3\wedge t_1^{\wedge }\right)$ 时，我们有

$\begin{array}{c}{\nu }^{1-\alpha }\left(t_2\right)\le {\lambda }^{1-\alpha }{\nu }^{1-\alpha }\left(t_2^{-}\right)\\ \le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)\left(t_2-t_1\right)}{\nu }^{1-\alpha }\left(t_2^{-}\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t_2-t_1\right)}\right)\right)\\ \le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)\tau }{\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\text{e}}^{-q\left(1-\alpha \right)\tau }\delta +\frac{1}{{\left(2\eta \right)}^{1-\alpha }}{\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\text{e}}^{-q\left(1-\alpha \right)\tau }{\mu }^{1-\alpha }\left(\left|x_0\right|\right)-\delta \right)\\ \le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -{\text{e}}^{-q\left(1-\alpha \right)\tau }\delta \end{array}$

及

$\begin{array}{c}{\nu }^{1-\alpha }\left(t\right)\le {\text{e}}^{-q\left(1-\alpha \right)\left(t-t_2\right)}{\nu }^{1-\alpha }\left(t_2\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t-t_2\right)}\right)\\ \le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-\delta -{\text{e}}^{-q\left(1-\alpha \right)\tau }\delta -\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_2}{t_3-t_2}}\right).\end{array}$

下面我们将证明

${\nu }^{1-\alpha }\left(t\right)\le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\displaystyle {\sum }_{i=0}^{k-1}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_k}{t_{k+1}-t_k}}\right)$， $\forall t\in \left[t_k,t_{k+1}\wedge t_1^{\wedge }\right)$。 (10)

现在假设在区间 $\left[0,t_k\right)$ 上，k满足 $1<k<N\left(t_1^{\wedge },0\right)$ 并且 $\forall t\in \left[t_m,t_{m+1}\right)$， $m=1,\cdots ,k-1$，可以得到

${\nu }^{1-\alpha }\left(t\right)\le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\displaystyle {\sum }_{i=0}^{m-1}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_m}{t_{m+1}-t_m}}\right)$。

在 $t\in \left[t_k,t_{k+1}\wedge t_1^{\wedge }\right)$ 上，由(8)式得到

$\begin{array}{c}{\nu }^{1-\alpha }\left(t_k\right)\le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)\left(t_k-t_{k-1}\right)}{\nu }^{1-\alpha }\left(t_{k-1}\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t_k-t_{k-1}\right)}\right)\right)\\ \le {\lambda }^{1-\alpha }\left({\text{e}}^{-q\left(1-\alpha \right)\tau }{\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\text{e}}^{-q\left(1-\alpha \right)\tau }{\displaystyle {\sum }_{i=0}^{k-2}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\tau }\right)\right)\\ \le {\lambda }^{1-\alpha }\left(\frac{1}{{\left(2\eta \right)}^{1-\alpha }}{\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\text{e}}^{-q\left(1-\alpha \right)\tau }{\displaystyle {\sum }_{i=0}^{k-2}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\delta \right)\\ \le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\displaystyle {\sum }_{i=0}^{k-1}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }.\end{array}$

及

$\begin{array}{c}{\nu }^{1-\alpha }\left(t\right)\le {\nu }^{1-\alpha }\left(t_k\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t-t_k\right)}\right)\\ \le {\mu }^{1-\alpha }\left(\left|x_0\right|\right)-{\displaystyle {\sum }_{i=0}^{k-1}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_k}{t_{k+1}-t_k}}\right).\end{array}$

所以(10)式在 $\forall t\in \left[t_k,t_{k+1}\wedge t_1^{\wedge }\right)$ 上成立。通过归纳法得出，当 $N\left(t_1^{\wedge },0\right)>0$ 时，(10)式对 $\forall t\in \left[0,t_1^{\wedge }\right)$ 都成立。如果 $t_1^{\wedge }=\infty$，则(10)式在 $\left[0,\infty \right)$ 上成立。如果 $t_1^{\wedge }<\infty$，则当 $t\in \left[t_l^{\wedge },t_l^{\vee }\right)$ 上时，由(5)和(7b)式得

$\nu \left(t\right)\le \frac{1}{\rho }\chi \left({\Vert \omega \Vert }_{[0,t]}\right)\le 2\eta \chi \left({\Vert \omega \Vert }_{[0,t]}\right)$。

当 $t\in \left[t_{l-1}^{\vee },t_l^{\wedge }\right)$ 上时，如果 $t_{l-1}^{\vee }$ 不是脉冲点，由(5)和(7a)式得

$\nu \left(t_{l-1}^{\vee }\right)\le \frac{1}{\rho }\chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)\le 2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)$。

如果 $t_{l-1}^{\vee }$ 是脉冲点，由(5)和(7b)式得

$\nu \left(t_{l-1}^{\vee }\right)\le \lambda \nu \left(t_{l-1}^{\vee -}\right)\le \frac{\lambda }{\rho }\chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)\le 2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)$。

当 $t\in \left(t_{l-1}^{\vee },t_l^{\wedge }\right)$ 上时，若 $N\left(t_l^{\wedge },t_{l-1}^{\vee }\right)=0$，则

${\nu }^{1-\alpha }\left(t\right)\le {\nu }^{1-\alpha }\left(t_{l-1}^{\vee }\right)-\frac{c}{q}\left(1-{\text{e}}^{-q\left(1-\alpha \right)\left(t-t_{l-1}^{\vee }\right)}\right)\le {\left(2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)\right)}^{1-\alpha }$。

若 $N\left(t_l^{\wedge },t_{l-1}^{\vee }\right)>0$，对于 $\forall t\in \left(t_{l-1}^{\vee },t_{{\xi }_l+1}\right)$，由(A₃)得 $\nu \left(t\right)\le \nu \left(t_{l-1}^{\vee }\right)$。对于 $t\in \left[t_{{\xi }_l+k},t_{{\xi }_l+k+1}\wedge t_l^{\wedge }\right)$， $k\in \left\{1,\cdots ,N\left(t_l^{\wedge },t_{l-1}^{\vee }\right)\right\}$，类似于(10)的证明，我们有

$\begin{array}{c}{\nu }^{1-\alpha }\left(t\right)\le {\left(2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)\right)}^{1-\alpha }-{\displaystyle {\sum }_{i=0}^{k-1}{\text{e}}^{-iq\left(1-\alpha \right)\tau }\delta }-\frac{c}{q}\left(1-{\text{e}}^{-\delta \frac{t-t_{{\xi }_l+k}}{t_{{\xi }_l+k+1}-t_{{\xi }_l+k}}}\right)\\ \le {\left(2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t_{l-1}^{\vee }\right]}\right)\right)}^{1-\alpha }.\end{array}$

所以，对于 $\forall t\in \left(t_{l-1}^{\vee },t_l^{\wedge }\right)$，可以得到 $\nu \left(t\right)\le 2\eta \chi \left({\Vert \omega \Vert }_{[0,t]}\right)$。结合(10)式，我们有，在 $t\in [0,\infty )$ 上， $\nu \left(t\right)\le {\beta }_2\left(\left|x_0\right|,t\right)\vee \left(2\eta \chi \left({\Vert \omega \Vert }_{[0,t]}\right)\right)$。

若情况(ii)成立，在这种情况下，证明方法与上面相同，我们最终可以证得

$\nu \left(t\right)\le 2\eta \chi \left({\Vert \omega \Vert }_{[0,t]}\right)$。

联立(A₁)和(6)式可以得到 ${\phi }_1\left(\left|x\left(t\right)\right|\right)\le \nu \left(t\right)\le {\beta }_2\left(\left|x_0\right|,t\right)\vee \left(2\eta \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)\right)$，即 $\left|x\left(t\right)\right|\le \beta \left(\left|x_0\right|,t\right)+\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$。这里 $\beta \left(s,t\right)={\phi }_1^{-1}\circ {\beta }_2\left(s,t\right)$ 是一个 $\mathcal{K}{\mathcal{L}}_0$ 函数， $\gamma \left(s\right)={\phi }_1^{-1}\left(2\eta \chi \left(s\right)\right)$ 是一个 ${\mathcal{K}}_{\infty }$ 函数。因此系统(1)在 $U_{\vartheta }$ 上对于任意脉冲序列 $\left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 是FTISS。得证。

注1：假设(A₃)保证了不具有脉冲效应时系统(1)是FTISS。故，当系统(1)受到稳定的脉冲扰动，即 $\eta \le 1$ 时，对于任意的脉冲频率 $\tau >0$，系统(1)都是FTISS的；当系统(1)受到不稳定的脉冲扰动影响，即 $\eta >1$ 时，定理2.1得到了系统(1)仍然保持FTISS性质的脉冲频率的下界，即

$\tau \ge \frac{1}{-q\left(1-\alpha \right)}\ln \left(\frac{\frac{c}{q}+{\left(\frac{\mu \left(\vartheta \right)}{2\eta }\right)}^{1-\alpha }}{\frac{c}{q}+{\mu }^{1-\alpha }\left(\vartheta \right)}\right)$。

注2：当系统(1)不具有脉冲扰动且假设(A₃)中 $q=0$ 时，定理2.1将退化成文献 [18] 中的结论。当假设(A₃)中 $q=0$ 时，定理2.1将退化成文献 [21] 中的结论。

注3：当 $\omega \left(t\right)\equiv 0$ 时，系统(1)将退化为无外部输入的脉冲非线性系统。此时，在定理2.1的条件下，系统(1)将FTS。文献 [22] 考虑了在脉冲扰动满足 $V\left(g\left(x,0\right)\right)\le V\left(x\right)$ 时系统FTS的结论，这种情况脉冲效应具有镇定性。而在定理2.1中，如果不考虑外部输入，(A₂)变成 $V\left(g\left(x,0\right)\right)\le \eta V\left(x\right)$， $\eta >1$。此时，脉冲效应将破坏系统的稳定性，所以脉冲不能太频繁的发生。

4. 数值模拟

本节给出两个数值例子说明本文中定理的正确性。

例1：考虑下面一维脉冲系统：

$\{\begin{array}{l}\stackrel{\dot{}}{x}\left(t\right)=-2x^{\frac{1}{3}}\left(t\right)-1.1x\left(t\right)+{\omega }^2\left(t\right),t\ne t_k,\\ x\left(t\right)=1.2x\left(t^{-}\right)+{\omega }^2\left(t^{-}\right),t=t_k.\end{array}$ (11)

假设初始状态 $x_0\in U_{\vartheta }$，其中 $\vartheta$ 是一个给定的正常数。选取 $V\left(x\right)=\left|x\right|$，则

$\begin{array}{c}\stackrel{\dot{}}{V}\left(x\left(t\right)\right)\le -2{\left|x\left(t\right)\right|}^{\frac{1}{3}}-1.1\left|x\left(t\right)\right|+{\omega }^2\left(t\right)\\ \le -2{\left|x\left(t\right)\right|}^{\frac{1}{3}}-0.1\left|x\left(t\right)\right|-\left(\left|x\left(t\right)\right|-{\omega }^2\left(t\right)\right)\\ \le -2V{\left(x\left(t\right)\right)}^{\frac{1}{3}}-0.1V\left(x\left(t\right)\right)\end{array}$，当 $V\left(x\left(t\right)\right)\ge {\omega }^2\left(t\right)$。

根据定理，当 $t=t_k$ 时， $V\left(g\left(x\left(t\right),\omega \left(t\right)\right)\right)=\left|1.2x\left(t^{-}\right)+{\omega }^2\left(t^{-}\right)\right|\le 1.2\left|x\left(t^{-}\right)\right|+{\omega }^2\left(t^{-}\right)$，这里 $\eta =1.2$ 和 $\chi \left(s\right)=s^2$。当 $t\ne t_k$ 时，取 $c=2$， $\alpha =1/3$， $q=0.1$ 则(3)式成立。因此，对于 $\forall \left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 且

$\tau \ge \frac{1}{-q\left(1-\alpha \right)}\ln \left(\frac{\frac{c}{q}+{\left(\frac{\mu \left(\vartheta \right)}{2\eta }\right)}^{1-\alpha }}{\frac{c}{q}+{\mu }^{1-\alpha }\left(\vartheta \right)}\right)=-15\ln \left(\frac{20+0.56{\mu }^{\frac{2}{3}}\left(\vartheta \right)}{20+{\mu }^{\frac{2}{3}}\left(\vartheta \right)}\right)$，

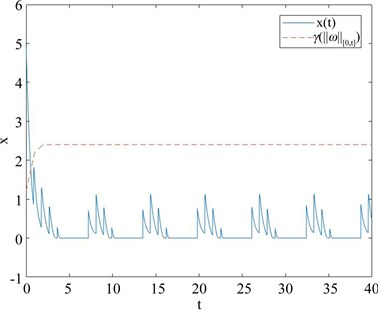
Figure 1. The trajectory of the system when $t=0.9k$

图1. 当 $t=0.9k$ 时的系统轨迹

则系统(11)是FTISS，这里 $\mu \left(\vartheta \right)$ 在定理2.1中已定义。取 $\vartheta =5$， $\omega \left(t\right)=0.5\left(1+\sin t\right)$ 此时， ${\Vert \omega \Vert }_{\infty }=1$ 和 $\mu \left(\vartheta \right)=5$，从而我们有冲频率 $\tau \ge 0.365$。在数值模拟中，取 $t_k=0.9k$， $k\in {\mathbb{Z}}_0$ 时， $\tau =0.9>0.365$，此时图1显示了系统(11)在初始状态 $x_0=5$ 时的轨迹在有限时刻进入 $\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 的界，此后并没有超过这个界。另一方面，在相同条件下，取 $t=0.3k$， $k\in {\mathbb{Z}}_0$，这不满足FDT的约束条件，从图2上可以看出轨道不时超过界 $\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$。

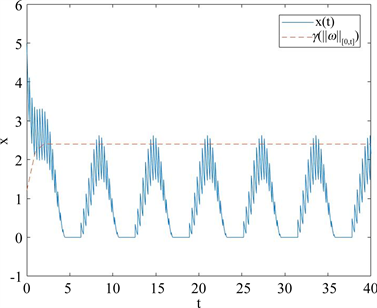
Figure 2. The trajectory of the system when $t=0.3k$

图2. 当 $t=0.3k$ 时的系统轨迹

注4：运用文献 [21] 的结论，我们得到只有当 $\tau \ge 0.968$ 时系统(11)才能达到FTISS。因此，我们的结论在估计脉冲频率上大大改进了文献 [21] 的结论。

例2：考虑一个三维脉冲系统：

$\{\begin{array}{l}{\stackrel{\dot{}}{x}}_1\left(t\right)=-\sqrt{\left|x_1\left(t\right)\right|}\text{sign}\left(x_1\left(t\right)\right)-3x_1\left(t\right)+x_2\left(t\right)+{\omega }_1\left(t\right),\\ {\stackrel{\dot{}}{x}}_2\left(t\right)=-\sqrt{\left|x_2\left(t\right)\right|}\text{sign}\left(x_2\left(t\right)\right)-3x_2\left(t\right)+x_3\left(t\right)+{\omega }_2\left(t\right),\\ {\stackrel{\dot{}}{x}}_3\left(t\right)=-\sqrt{\left|x_3\left(t\right)\right|}\text{sign}\left(x_3\left(t\right)\right)-3x_3\left(t\right)+x_1\left(t\right)+{\omega }_3\left(t\right),\end{array}t\ne t_k$, (12)

脉冲点满足

$x\left(t\right)=Ax\left(t^{-}\right)+B\omega \left(t^{-}\right)$， $t=t_k$。 (13)

这里 $x\left(t\right)={\left(x_1\left(t\right),x_2\left(t\right),x_3\left(t\right)\right)}^{\text{T}}$， $\omega ={\left({\omega }_1\left(t\right),{\omega }_2\left(t\right),{\omega }_3\left(t\right)\right)}^{\text{T}}$， $\left\{t_k\right\}\in {\mathcal{F}}_{\tau }$，并且

$A=\left(\begin{array}{ccc}1.4& 0.1& 0.2\\ 0& 1.3& 0\\ 0& 0& 1.1\end{array}\right)$， $B=\left(\begin{array}{ccc}0.3& 0.1& 0.1\\ 0.1& -0.1& 0.2\\ 0& 0& 0.2\end{array}\right)$。

假设初始状态 $x_0\in U_{\vartheta }$， $\vartheta >0$ 是一个给定的常数。选取 $V\left(x\right)=x^{\text{T}}x$，对 $x\in {ℝ}^3$，则

$\begin{array}{c}\stackrel{\dot{}}{V}\left(x\right)=2x_1\left(t\right)\left(-\sqrt{\left|x_1\left(t\right)\right|}\text{sign}\left(x_1\left(t\right)\right)-3x_1\left(t\right)+x_2\left(t\right)+{\omega }_1\left(t\right)\right)\\ +2x_2\left(t\right)\left(-\sqrt{\left|x_2\left(t\right)\right|}\text{sign}\left(x_2\left(t\right)\right)-3x_2\left(t\right)+x_3\left(t\right)+{\omega }_2\left(t\right)\right)\\ +2x_3\left(t\right)(-\sqrt{\left|x_3\left(t\right)\right|}\text{sign}\left(x_3\left(t\right)\right)-3x_3\left(t\right)+x_1\left(t\right)+{\omega }_3(\; t\; ))\end{array}$

$\begin{array}{l}\le -2{\left|x_1\left(t\right)\right|}^{\frac{3}{2}}-6x_1^2\left(t\right)+2x_1\left(t\right)x_2\left(t\right)+2x_1\left(t\right){\omega }_1\left(t\right)\\ -2{\left|x_2\left(t\right)\right|}^{\frac{3}{2}}-6x_2^2\left(t\right)+2x_2\left(t\right)x_3\left(t\right)+2x_2\left(t\right){\omega }_2\left(t\right)\\ -2{\left|x_3\left(t\right)\right|}^{\frac{3}{2}}-6x_3^2\left(t\right)+2x_1\left(t\right)x_3\left(t\right)+2x_3\left(t\right){\omega }_3(\; t\; )\end{array}$

$\begin{array}{l}\le -2\left({\left|x_1\left(t\right)\right|}^{\frac{3}{2}}+{\left|x_2\left(t\right)\right|}^{\frac{3}{2}}+{\left|x_3\left(t\right)\right|}^{\frac{3}{2}}\right)-6\left(x_1^2\left(t\right)+x_2^2\left(t\right)+x_3^2\left(t\right)\right)\\ +3\left(x_1^2\left(t\right)+x_2^2\left(t\right)+x_3^2\left(t\right)\right)+{\omega }_1^2\left(t\right)+{\omega }_2^2\left(t\right)+{\omega }_3^2\left(t\right)\\ \le -c{V}^{\alpha }\left(x\left(t\right)\right)-qV\left(x\left(t\right)\right)\end{array}$，当 $V\left(x\left(t\right)\right)\ge \chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$。

这里 $c=2$ ， $\alpha =3/4$ ， $q=2$ ，则定理1的(3)式成立。对于 $t=t_k$，我们可以得到

$\begin{array}{c}V\left(x\left(t\right)\right)={\left(Ax\left(t^{-}\right)+B\omega \left(t^{-}\right)\right)}^2\\ =x^{\text{T}}\left(t^{-}\right)A^{\text{T}}Ax\left(t^{-}\right)+x^{\text{T}}\left(t^{-}\right)A^{\text{T}}B\omega \left(t^{-}\right)+{\omega }^{\text{T}}\left(t^{-}\right)B^{\text{T}}Ax\left(t^{-}\right)+{\omega }^{\text{T}}\left(t^{-}\right)B^{\text{T}}B\omega \left(t^{-}\right)\\ \le 2x^T\left(t^{-}\right)A^{\text{T}}Ax\left(t^{-}\right)+2{\omega }^{\text{T}}\left(t^{-}\right)B^{\text{T}}B\omega \left(t^{-}\right)\\ \le 2{\lambda }_{\max }\left(A^{\text{T}}A\right)x^{\text{T}}\left(t^{-}\right)x\left(t^{-}\right)+2{\lambda }_{\max }\left(B^{\text{T}}B\right){\omega }^{\text{T}}\left(t^{-}\right)\omega \left(t^{-}\right)\\ :=\eta V\left(x\left(t^{-}\right)\right)+\chi \left({\Vert \omega \Vert }_{\left[0,t\right]}\right).\end{array}$

这里 $\eta =3.92$， $\chi \left(s\right)=0.2s^2$。那么对于任意给定的脉冲时间序列

$\left\{t_k\right\}\in {\mathcal{F}}_{\tau }$ 且 $\tau \ge -2\ln \left(\frac{1+0.6{\mu }^{\frac{1}{4}}\left(\vartheta \right)}{1+{\mu }^{\frac{1}{4}}\left(\vartheta \right)}\right)$。

取 ${\omega }_i\left(t\right)=0.5\left(1+\cos t\right)$， $i=1,2,3$， $\vartheta =2$,则 $\mu \left(\vartheta \right)=2$。从而，我们可以得到 $\tau \ge 0.49$ 时系统(12) FTISS。图3显示了系统(12)和(13)在选取 $t_k=0.7k$， $k\in {\mathbb{Z}}_0$，此时 $\tau =0.7>0.49$，及初始时刻分别为 $x_0={\left(1.5,0.5,-0.5\right)}^{\text{T}}$， ${\left(0.8,0.5,1.5\right)}^{\text{T}}$， ${\left(-1.5,0,0.5\right)}^{\text{T}}$， ${\left(0.5,1.3,1.5\right)}^{\text{T}}$ 时的轨迹在有限时刻进入 $\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$ 的界，此后并没有超过这个界。另一方面，在相同条件下，取 $t=0.3k$， $k\in {\mathbb{Z}}_0$， $\tau =0.3<0.49$，这不满足FDT的约束条件，从图4上可以看出轨道不时超过界 $\gamma \left({\Vert \omega \Vert }_{\left[0,t\right]}\right)$。

Figure 3. The trajectory of the system when $t=0.7k$

图3. 当 $t=0.7k$ 时的系统轨迹

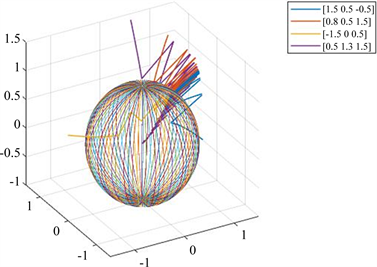
Figure 4. The trajectory of the system when $t=0.2k$

图4. 当 $t=0.2k$ 时的系统轨迹