基于评价体系与最优化的原材料订购和运输问题研究

Research on Raw Material Ordering and Transportation Based on Evaluation System and Optimization

摘要: 本文以2021年高教社杯数学建模题目生产企业原材料的订购与运输为基础，设计供应商的评价模型和供应链优化模型，建立多目标规划和0-1规划，并采用TOPSIS法设计评价算法，构建了求解最优订购方案和最优运输方案的数学模型，对现实中存在第三方物流的企业具有现实意义。

Abstract: In this paper, based on the mathematical modeling topic of 2021 Higher Education Community Cup, raw material ordering and transportation of production enterprises, the evaluation model of suppliers and supply chain optimization model are designed, multi-objective programming and 0-1 programming are established, and the TOPSIS method is used to design the evaluation algorithm, and the mathematical model for solving the optimal ordering scheme and the optimal transportation scheme is constructed. It is of practical significance to the enterprises which have the third party logistics in reality.

1. 引言

近年来，国家经济发展、社会化程度日益成熟，人民生活水平不断提高。消费观念的转变，使得消费目标不再局限于本地供应商。席卷全球的新冠肺炎和变化万千的国际形势都开始影响全球供应链。2020年4月，习近平总书记前瞻性地提出了建立以国内大循环为主体、国内国际双循环相互促进的新发展格局 [1] 。而为提高供应链供给速度和服务质量，第三方物流成为供应链管理过程中最为重要的环节，其直接影响到用户的深层次体验，并通过与供应链成员之间的互动了解到不同成员的需求 [2] 。企业不断提高自己的生产水平，提高产品品质，并不断扩大销售渠道，其核心竞争力的提升有助于企业扩大规模。而要达到以上目标，一方面，要选择质量上乘、费用较低的原材料供应商，从而达到规模化生产的目标。另一方面企业将物流外包，将更多的精力投身于生产之中，大大提高了产品质量。因此选择优质的原材料供应商和第三方物流服务商成为企业规模化发展的重要因素。选择原材料供应商，企业要考虑原材料质量、价格、供货稳定性、企业信用等，而选择第三方物流公司，企业需要考虑其费用、安全性、信用度等因素。因此作者结合实际，建立起综合性的评价模型和最优化模型，解决以上问题。

2. 预备知识

TOPSIS法 [3] 是根据有限个评价对象与理想化目标的接近程度进行排序的方法，是在现有的对象中进行相对优劣的评价。TOPSIS法是多目标决策分析中一种非常有效的方法。又称为优劣解距离法。其计算复杂度小，经常用于评价类模型的求解。主要步骤包括原始矩阵正向化处理、标准化处理、归一化处理、权重得分计算。

规划模型 [4] 是企业用来实现目标管理的一种线性规划模型。目标规划是解决企业多目标管理的有效方法，它是按照决策者事前确定的若干目标值及其实现的优先次序，在给定的有限资源下寻找偏离目标值最小的解的数学方法。

3. 问题假设与符号说明

3.1. 问题假设

· 假设生产企业在初始阶段原材料的储存量为0；

· 为保证生产，假设生产企业需要保持不少于两周的生产库存；

· 假设供应商以及转运商的供应链会延续之前的规律继续进行；

· 假设没有突发因素对供货转运和企业生产的影响。

3.2. 符号说明

$x_{ij}\left(i=1,2,\cdots ,402;j=1,2,\cdots ,48\right)$ 表示在第i家供应商第j周的订货量；

$y_{ij}\left(i=1,2,\cdots ,402;j=1,2,\cdots ,48\right)$ 表示第i家供应商第j周的供货量；

a_i表示在第i家供应商供货量大于订货量的周数；

b_i表示在第i家供应商订货量不为0的周数；

r_i表示反映第i家供应商的供货率；

h_i表示第i家供应商的周平均供货量缺失；

${\bar{y}}_i$ 表示第i家供应商周平均供货量；

$S_i^2$ 表示第i家生产企业周供货量的均方差。

4. 模型建立与求解

4.1. 问题一分析

旨在建立合理的供货商评价指标和评价模型对402家供货商作评价。选择出50家优质的供货商以保证企业的正常运转。

4.1.1. 模型建立

供货质量和稳定性是评价供应商实力的重要评价指标，根据问题背景，本问题着重考虑供货的稳定性。因企业的原材料需求以周为周期，故将评价标准设为周供货量均值。

${\bar{y}}_i=\frac{{\displaystyle \underset{j=1}{\overset{240}{\sum }}{y}_{ij}}}{b_i},i=1,2,\cdots ,402$

在实际供货中，订单的执行通常不会按照订单要求。从顾客让渡价值的角度上说，只有买手在供货商处所投入的实际成本和机会成本获得了更高的价值回报时，买手才能进行重复性购买，这样双方才能获得长期的、稳定的合作关系，从而减少沟通时间和成本 [5] 。因此供货商的信用度也是评价供货商很重要的指标。本文将及时到货程度作为信用的评价指标，定义周平均供货量缺失为：

$h_i=\frac{{\displaystyle \underset{j=1}{\overset{240}{\sum }}\left(x_{ij}-y_{ij}\right)}}{b_i},i=1,2,\cdots ,402$

供货的稳定性决定了企业生产的稳定性，因此，企业希望供应商能满足需求的同时，可连续稳定连续供货更为重要。定义供货率为：

$r_i=\frac{a_i}{b_i},i=1,2,\cdots ,402$

供货的及时度反映了供货商的可靠性，生产企业容易出现因为材料不足而暂停生产，从而导致产品生产进度被延误，此时供应商可能需要对这类情况导致的顾客的损失进行赔偿 [6] 。

因此，引入均方差作为评价指标，衡量供应商供货的可靠性。

$S_i^2=\frac{{\displaystyle \underset{j=1}{\overset{240}{\sum }}{\left(x_{ij}-y_{ij}\right)}^2}}{240b_i},i=1,2,\cdots ,402$

4.1.2. 基于TOPSIS法 [7] 评价算法

Step 1 设置周订货量与周供货量的标准误差最小的极小化指标

${x^{\prime }}_{ij}=M-x_{ij}$

M为标准误差取值的最大值。

Step 2 极小值指标均方差转化为极大型指标 $\max \left\{-S_i^2\right\}$

1) 供货率指标转化为极大型指标， $r_i$ 最佳数值为1。正向化公式如下：

$M=\max \left\{\left|r_i-1\right|\right\},r_i=1-\frac{\left|r_i-1\right|}{M}$

2) 未供货量指标转化为极大型指标 [8] ，未供货量为区间型指标，最佳区间[0, 5445.7]，那么正向化公式为：

$M=\max \left\{-h_i,\left(\max \left\{h_i\right\}-5445.7\right)\right\}$

$\begin{array}{l}{h}_i=\{\begin{array}{l}1-\frac{0-x_{ij}}{M},x_{ij}<0\\ 1,0\le x_{ij}\le 5445.7\\ 1-\frac{x_{ij}-5445.7}{M},x_{ij}>5445.7\end{array}\\ i=1,2,\cdots ,402;j=1,2,\cdots ,240\end{array}$

Step 3 构造归一化初始矩阵 [9]

根据本问题需要402个供应商作为待评价对象，评价指标有供应率、未供应量、供货量均值、供货量均方差四个指标，但仅3个指标(属性)可作为归一化变量，则原始数据矩阵构造为：

$A={\left(\begin{array}{ccc}{a}_{11}& a_{12}& a_{13}\\ a_{21}& a_{22}& a_{23}\\ a_{31}& a_{32}& a_{33}\\ ⋮& ⋮& ⋮\\ a_{n1}& a_{n2}& a_{n3}\end{array}\right)}_{n\times 3}$

使用余弦距离度量实现归一化，将每列元素都除以当前列向量的范数。

$Z_{ij}=\frac{a_{ij}}{\Vert a_{ij}\Vert }$

由此得到归一化处理后的标准化矩阵Z

$Z={\left(\begin{array}{ccc}{z}_{11}& z_{12}& z_{13}\\ z_{21}& z_{22}& z{}_{23}\\ z_{31}& z_{32}& z_{33}\\ ⋮& ⋮& ⋮\\ z_{n1}& z_{n2}& z_{n3}\end{array}\right)}_{n\times 3}$

Step 4 确定最优方案，Z⁺由Z中每列元素的最大值构成，Z⁻由Z中每列元素的最小值构成

$Z^{+}=\left\{\max \left(z_{11},z_{21},\cdots ,z_{n1}\right),\max \left(z_{12},z_{22},\cdots ,z_{n2}\right),\max \left(z_{13},z_{23},z_{n3}\right)\right\}=\left\{Z_1^{+},Z_2^{+},Z_3^{+}\right\}$

$Z^{-}=\left\{\min \left(z_{11},z_{21},\cdots ,z_{n1}\right),\min \left(z_{12},z_{22},\cdots ,z_{n2}\right),\min \left(z_{13},z_{23},z_{n3}\right)\right\}=\left\{Z_1^{-},Z_2^{-},Z_3^{-}\right\}$

Step 5 算各指标的熵值

$e_j=-k{\displaystyle \underset{i=1}{\overset{n}{\sum }}{Z}_{ij}}\ln Z_{ij}\left(j=1,2,3\right)$

Step 6 加权处理

$D_i^{+}=\sqrt{{\displaystyle \underset{j=1}{\overset{3}{\sum }}{w}_j{\left(Z_j^{+}-z_{ij}\right)}^2}},D_i^{-}=\sqrt{{\displaystyle \underset{j=1}{\overset{3}{\sum }}{w}_j{\left(Z_j^{-}-z_{ij}\right)}^2}}$ ，

其中 $w_j=\left[w_A,w_B,w_C\right]$ 。

Step 7 计算各评价对象与最优方案的贴近程度C_j

$C_j=\frac{D_i^{-}}{D_i^{+}+D_i^{-}}$

$0\le C_i\le \text{1}$ , $C_i\to \text{1}$ 表明评价对象越优。

4.1.3. 运行结果

根据以上模型的求解，根据程序运行选择出得分最高的50家供应商，如表1所示。

Table 1. List of Top 50 suppliers score

表1. 50家最优供应商得分列表

4.2. 问题二分析

4.2.1. 最少供应商方案

根据问题一的结果，50家供货商提供原材料A、B、C的数量要求满足企业生产的需要，并要选择尽可能少的供货商提供要求。通过对50家优质供货商的分析，设定供货偏好权重，对供货商进行供货分配 [10] 。引入0-1规划解决供货商选择，目标函数则为选择供货商总数最小。

引入决策变量

$x_i=\{\begin{array}{l}1,选择供应商提供服务\\ 0,不选择供应商提供服务\end{array}$

构造矩阵 $X=\left\{x_1,x_2,\cdots ,x_i\right\}$ 为最优解。

根据选择出的50家优质供应商的供货情况，规定供货权重为A、B、C三种原材料的供货均值，做供应商选择偏好指标，进行归一化处理可得：

$\left[w_A,w_B,w_C\right]=\left[0.347,0.349,0.304\right]$

原材料供货商分类矩阵：A_i、B_i、C_i 分别表示第i个提供原材料A、B、C的商家。

$A=\left(\begin{array}{c}{A}_1\\ A_2\\ ⋮\\ A_t\end{array}\right),B=\left(\begin{array}{c}{B}_1\\ B_2\\ ⋮\\ B_m\end{array}\right),C=\left(\begin{array}{c}{C}_1\\ C_2\\ ⋮\\ C_k\end{array}\right)$

其中 $t+m+k\le 50$ 。

50家优质供应商提供A、B、C三种原材料的供货量不大于对应供货总量。设产能 $S=2.82\times {10}^4$ ，分类供货总量加权计算。

选择供货总数最小为目标函数，即

$\min {\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i}$

s.t

$\{\begin{array}{l}XA\le \frac{w_{A}S}{W_A},XB\le \frac{w_{B}S}{W_B},XC\le \frac{w_{C}S}{W_C}\\ t+m+k\le 50\\ n\le 50\\ x_i=\left\{0,1\right\}\end{array}$

其中W为A、B、C三种原材料的生产所需，根据数据为 $\left[W_A,W_B,W_C\right]=\left[0.6,0.66,0.72\right]$ 。

4.2.2. 最经济原材料定购方案

为了得到最经济的采购方案，通过计算，可得到A、B、C 三种原材料的单位生产成本，如表2所示。

Table 2. Unit production cost

表2. 单位生产成本

显然，从经济效果上，A = C > B，而由于生产所需的单位C > A。综合考虑，原材料的选择优先顺序为A > C > B。即尽可能选择A、C原材供货商。因此将模型修正为

$x_i^A=\{\begin{array}{l}1,选择供应商A提供服务\\ 1,不选择供应商A提供服务\end{array}$

$x_i^B=\{\begin{array}{l}1,选择供应商B提供服务\\ 1,不选择供应商B提供服务\end{array}$

$x_i^C=\{\begin{array}{l}1,选择供应商C提供服务\\ 1,不选择供应商C提供服务\end{array}$

不妨设 $X={\left(x_1^A,x_2^A,\cdots ,x_t^A\right)}^{\text{T}},Y={\left(x_1^B,x_2^B,\cdots ,x_m^B\right)}^{\text{T}},Z={\left(x_1^C,x_2^C,\cdots ,x_k^C\right)}^{\text{T}}$ 。

根据表1， $t_i^A,t_i^B,t_i^C$ 分别为A，B，C三种原材料供应商的得分指标，构造矩阵

$\tilde{A}=\left(t_1^A,t_2^A,\cdots ,t_t^A\right),\tilde{B}=\left(t_1^B,t_2^B,\cdots ,t_m^B\right),\tilde{C}=\left(t_1^C,t_2^C,\cdots ,t_k^C\right)$

$A={\left(t_1^A{x}_1^A,t_2^A{x}_2^A,\cdots ,t_t^A{x}_t^A\right)}^{\text{T}},B={\left(t_1^B{x}_1^B,t_2^B{x}_2^B,\cdots ,t_m^B{x}_m^B\right)}^{\text{T}},C={\left(t_1^C{x}_1^C,t_2^C{x}_2^C,\cdots ,t_k^C{x}_k^C\right)}^{\text{T}}$

综合考虑上述各种因素，通过分析50家供应商，同时选择供货总数最小为目标建立优化模型：

$\min \left({\displaystyle \underset{i=1}{\overset{n}{\sum }}{x}_i^A}+{\displaystyle \underset{i=1}{\overset{m}{\sum }}{x}_i^B}+{\displaystyle \underset{i=1}{\overset{t}{\sum }}{x}_i^C}\right)$

s.t.

$\{\begin{array}{l}t+m+k\le 50\\ XA\le \frac{S}{W_A},XB\le \frac{S}{W_B},XC\le \frac{S}{W_C}\\ \frac{XA}{W_A}+\frac{XB}{W_B}+\frac{XC}{W_C}\ge S\\ x_i^A=\left\{0,1\right\},x_i^B=\left\{0,1\right\},x_i^C=\left\{0,1\right\}\\ {\displaystyle \underset{i=1}{\overset{t}{\sum }}{x}_i^A}>{\displaystyle \underset{i=1}{\overset{m}{\sum }}{x}_i^B}>{\displaystyle \underset{i=1}{\overset{k}{\sum }}{x}_i^C}\end{array}$

4.2.3. 损耗最少的转运方案 [10]

大量的损耗会增加生产成本，因此对于转运商质量的要求也非常重要。根据问题分析，需要解决两个问题。第一，供应商选择数量最少，并且满足每次运转过程转运商与供货商一一对应；第二，满足转运商再次转运的最大容量为6000。由于并没有明确转运商的产能，以供货质量的均值作为供货量的标准。按周进行转运商的分配。对于各家转运商而言，损耗越小，其稳定性和可靠性越靠前。对于企业而言，稳定性和可靠性同时高的转运商会增加企业的经济效益。

240周的平均损耗率作为转运商损耗率，这个假设是合理的。要建立使损耗最小的数学模型，即目标函数为：

$\min {\displaystyle \underset{i=1}{\overset{50}{\sum }}{\displaystyle \underset{j=1}{\overset{8}{\sum }}{r}_{ij}{x}_{ij}}}$

其中r_ij表示由第j个转运商完成第i个供应商的损耗率。

$x_{ij}=\{\begin{array}{l}1,第j个转运商执行第i个供应商的转运任务\\ 0,第j个转运商不执行第i个供应商的转运任务\end{array}$

目标函数限制为每个供货商仅仅由一个转运商服务，因此约定条件为：

${\displaystyle \underset{i=1}{\overset{50}{\sum }}{\displaystyle \underset{j=1}{\overset{8}{\sum }}{x}_{ij}}}=1$

还应满足 ${\displaystyle \underset{i=1}{\overset{50}{\sum }}{\displaystyle \underset{j=1}{\overset{8}{\sum }}{p}_i{x}_{ij}}}\le 6000$ ，p_i表示50家供货商的平均供货量。

4.2.4. 模型求解

用lingo软件与python程序结合对模型进行求解，该企业至少选择36家供应商供应原材料才能满足生产需要。具体结果由图1所示。

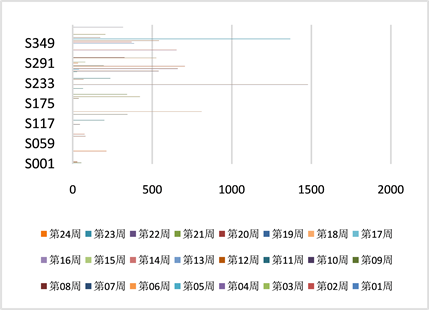
Figure 1. 24-weeks raw material order plan

图1. 24周原材料订购方案

图1和图2展示出优秀的转运商和供货商。稳定的供货能力和转运能力是企业稳定发展的基础。B材料的生产成本最高，A、C生产成本相同，36家供应商对A、B、C三种原材料平均供应需求依次是A > C > B；根据表2看出制定的240周原材料订购方案中使得供应量稳定，考虑尽量选择A、C原材料供应商，减少库存积压费用，使得企业的生产成本降低。

Figure 2. Transfer of raw materials

图2. 原材料转运情况

根据图3分析八家转运商平均损耗率可以看出T3 < T6 < T4 < T8 < T2 < T5 < T1 < T7。在选择转运商时应该避免损耗率较高的转运商；根据图4可知，原材料损耗率低的供应商转运次数并不低。所以在转运方案结合转运的损耗率和转运能力综合考虑，做到低损耗高转运，使得企业利益更大化。

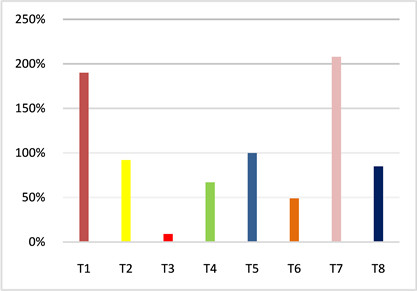
Figure 3. Average loss rate of transporters

图3. 转运商平均损耗率

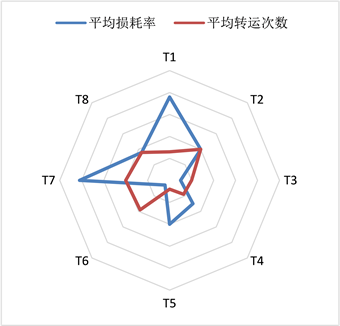
Figure 4. Average raw material loss and transfer times

图4. 原材料平均损耗与转运次数

5. 结论

目标规划在企业生产、销售、经营过程中都具有应用基础。企业能更清晰的认识到自身发展的问题，强化成本意识，扩大销售渠道，这就需要结合自身特点，综合分析企业中的各种因素，将最优化思想和目标规划思想运用在企业发展规划之中。使得企业发展更加具有科学性。

基金项目

四川省社会科学重点研究基地——彝语言文化中心项目《彝族数学文化融入数学教育的实践路径研究》(YZWH2225)。