1. 引言
身蕴藏量巨大、调节性灵活等特点,在电网调峰中占据着越来越重要的地位;同时,梯级水电系统的开发能够充分地利用水电资源,对改善生态环境有着十分重要的意义。目前,随着水电资源的迅猛发展,我国已位居世界水电装机容量第一,不断增大的装机容量也使得梯级库群的优化调度求解问题变得更加的高维和复杂,求解过程变得十分艰难。如何精确高效求解大规模梯级库群的长期调度问题,保证水电系统的安全运行,已经成为一个重大难题 [1] 。
传统动态规划(DP)、线性规划(LP)可以有效获得高精度下的目标函数的最优解,但对于大规模水库调度问题,往往会导致求解速度缓慢,难以应用在实际调度问题中。动态规划的改进算法,如离散微分动态规划(DDDP),随机动态规划(SDP)等,虽然对DP算法进行了一定程度上的改进,有效缓解了传统动态规划算法的维数灾问题,但还是难以满足实际库群调度的实时性需求。冯仲恺等人以逐步优化算法为基础,进行了算法上的改进,提出了均匀逐步优化算法,虽然有效地降低了求解的规模,一定程度避免了维数灾问题,但容易过早地陷入局部最优解 [2] 。除传统算法之外,智能算法由于结构简单、易于实现等特点,也被广泛地应用到梯级库群的优化调度中,如王建群等人提出狼群算法(WPS) [3] 、纪昌明等人提出免疫蛙跳算法(ISFLA) [4] 、徐刚等人提出了一种蚁群算法(ACO) [5] 、王文川等人提出群居蜘蛛优化算法(SSO) [6] 、向波等人提出了一种免疫粒子群算法(IA-PSO) [7] 、钟平安等人提出了综合改进差分进化算法(UCG-MDE) [8] 、明波等人提出改进布谷鸟算法(CS) [9] [10] 、董亚迪提出了一种基于多Agent的人工鱼群算法(MAAFSA) [11] 、王森等人提出了一种自适应混沌整体退火遗传算法(SCWAGA) [12] [13] 等。但由于梯级库群优化调度是多维数、非线性、多阶段的优化组合问题,一般待优化的决策变量会达到百维甚至更高的高度,传统智能算法面对如此高维复杂的过程易于陷入局部最优解的情况,难以得到最优的目标值。鸟群算法(Bird Swarm Algorithm, BSA)是由Xianbing Meng [14] 等人于2015年提出的一种基于鸟群行为的新型生物启发式算法,其思想源于鸟群的飞行、觅食和警戒三个主要群体行为,通过鸟群之间的基本生物行为和觅食过程中的信息共享机制来完成对全局最优解的获取,该算法具有收敛速度快、鲁棒性强、收敛精度高的优势,已成功应用于多个水电调度领域,可用来改善梯级库群求解过程中维数过高、耗时过长等局限性 [3] 。以西南某流域大型水电基地中7座梯级水电站为例进行仿真模拟,以验证所提方法的合理性与有效性 [4] 。
2. 长期优化调度模型
2.1. 目标函数
(1)
(2)
式中,
为调度期内梯级各电站总发电量,kWh;
为电站i在t时段的平均出力,kW;
为时段t的小时数,h;
为电站i的出力系数;
为电站i在时段t的发电流量,m3/s;
为电站i在时段t的发电水头,m;N为梯级电站数;T为调度时段总数,T取1年;i对应为梯级库群中的水电站序号;t对应为调度期内的时段序号 [14] 。
2.2. 约束条件
1) 水量平衡方程
(3)
式中,
和
分别为电站 在时段t + 1和时段t的初始库容,m³;
、
、
分别为电站 在 时段的入库流量、发电流量、弃水流量,m3/s,正常情况下为了防止水力资源的浪费,梯级库群的弃水均为0。
2) 梯级间水力联系
(4)
式中,
为水电站i在时段t内的区间流量,m3/s;
为水电站i − 1在时段t内的出库流量,m3/s。
3) 水库流量关系
(5)
式中,
为水电站i在时段t内的出库流量,m3/s。
4) 水位约束
(6)
式中,
为电站i在时段t的初始水位,m;
、
分别为电站i在时段t的水位上下限m。
5) 始末水位控制约束
(7)
式中,
为电站i的初始水位,m;
为电站i的调度期末水位m。
6) 发电流量约束
(8)
式中,
、
分别为电站i在时段t的发电流量上下限,m³/s。
7) 出库流量约束
(9)
式中,
、
分别为电站i在时段t的出库流量上下限,m³/s。
8) 电站出力约束
(10)
式中,
、
分别为电站i在时段t的出力上下限,kW。
9) 梯级系统出力约束
(11)
式中,
为梯级系统在时段t的出力下限,kW。
10) 水位库容关系
(12)
式中,
为水电站i的水位库容函数关系。
11) 尾水位出库流量关系
(13)
式中,
为水电站i在时段t的平均尾水位,m;
为水电站i的尾水位出库流量函数关系。
12) 水头计算公式
(14)
式中,
为水电站i在时段t的水头,m。
13) 水头耗水率约束
(15)
式中,
为水电站n的水头–耗水率函数关系。
3. 鸟群算法
3.1. 鸟群算法介绍
鸟群算法(bird swarm algorithm, BSA)是依据鸟群行为所提出的一种仿生智能优化算法,BSA算法核心主要源于鸟群的飞行、觅食和警戒三个主要群体行为,其中鸟群的飞行行为可以让BSA算法跳出局部最优进行全局搜索,防止陷入局部最优的境地;鸟群的觅食行为可以为BSA算法记录个体和群体最好的解,鸟群觅食行为和警戒行为的随机切换可以让BSA算法去搜索当前局部的最优解,而通过鸟群的飞行间隔来平衡算法全局搜索和局部搜索的能力。BSA算法可以将规则简化描述:
1) 鸟群中的每只鸟可以在觅食和警戒行为之间随机切换。
2) 觅食期间,每只鸟可以迅速记录与更新个体和群体之间最好的觅食经验,这个经验将用于觅食,群体信息将即刻共享于整个鸟群。
3) 保持警戒的时候,每只鸟都试图向群体中心靠近,而具有较高食物储量的鸟类更倾向于向群体中心靠近。
4) 鸟类可以周期性地向其他位置移动。当移动到另一个位置时,鸟类一般要在生产者和乞讨者之间作出选择,具有最高食物储量的鸟将成为生产者,而具有最低食物储量的鸟将成为乞讨者,其他鸟将随机选择成为生产者和乞讨者。
5) 生产者积极寻觅食物,乞讨者随机跟随一个生产者寻找食物。
3.2. 基于梯级库群发电量最大模型的鸟群算法求解步骤
BSA智能算法求解梯级库群的主要思想流程为:以各时段水位为决策变量,梯级发电量最大为目标函数,鸟群在觅食和警戒下不断更新位置的行为可视为水库水位不断决策的过程,每个位置点代表着不同时段下的水位;将梯级库群长期优化调度中对应的各种约束以惩罚函数的形式表示 [6] ,鸟群在飞行过程中所记录的各个最优点就是水库水位最优离散点的组合。BSA算法的求解流程 [7] 如图1所示:
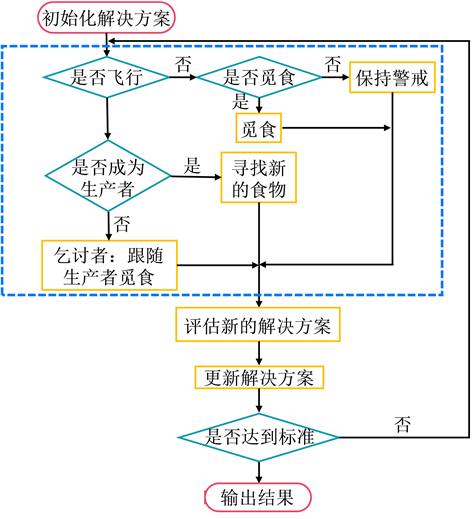
Figure 1. Solution flow of BSA algorithm
图1. BSA算法求解流程
4. 算例研究
4.1. 工程背景和参数设置
以我国西南地区某特大流域为背景进行研究。该流域的径流以降水量补给为主,以地下水和融雪补给为辅,每年的6月到10月为汛期,11月到次年5月为枯期。同时,该流域的水电基地是集中技术力量开发的世界级的水电基地之一,在我国西电东送战略中占有着关键的席位。选择该流域电站A、B、C、D、E、F、G,7座梯级库群为研究对象,各电站的基本参数见表1。这7座电站的总装机容量达1234万kW,A、E、F和G水电站属于季调节及以上的电站,调节性能较好,B和D属于日调节水电站,在长期优化调度中固定发电水头,仅考虑其发电效益。


Table 1. Basic parameters of cascade reservoirs in a basin in southwest China
表1. 西南某流域梯级库群基本参数
本文采用Python语言编程来实现BSA算法在梯级库群中的长期优化调度的求解,以发电量最大为目标函数,计算参数设置如下:
1) 分别选择研究中梯级库群的典型枯水、平水、丰水年为调度周期,以月为计算时段;
2) 梯级库群上每个电站的水位约束上限为正常蓄水位,水位约束下泄为死水位;
3) 梯级库群上每个电站的发电流量约束上限为最大引用流量,约束下泄为0;
4) 梯级库群上每个电站的出力约束上限为装机容量,出力约束下限为0;
5) 模型计算中不考虑弃水作用,每个电站时段的弃水量为0;
6) 长期优化调度中的发电量最大模型要求固定始末水位,不同典型年的始末水位不同。
7) 设置决策变量的规模N和维度M;
8) 水位离差步长step = 0.1 m。
4.2. 计算结果分析
为了验证BSA算法的适用性,分别选取该流域梯级枯期中的典型枯水、平水、丰水年为调度周期进行模拟计算。将梯级库群多年径流的实际运行数据进行从小到大排序,按照10%、50%、90%的频率选取典型的丰水、平水、枯水年,最终分别选择2019、2018、2020为典型枯水、平水、丰水年,每个典型年份的起调水位和末水位按实际运行数据决定。由于BSA算法自身的寻优机制,对梯级库群长期优化调度求解时,计算过程包含一定的随机性,研究中将取100次的运行结果中的最大值为梯级库群的最优发电量,取100次的平均耗时为实际的计算耗时,这样可以有效地避免随机性对优化结果的影响 [3] 。最终各电站和总的发电量结果如表2所示,季调节以上的电站A、电站E、电站F和电站G的典型枯水、平水、丰水年的年内调度过程分别由表3、表4、表5所示。

Table 2. Power generation in different typical years
表2. 不同典型年下的发电量
从表2中可得,BSA算法对研究中流域上的梯级库群进行长期优化调度时,由于天然径流的大小不同,对应的典型枯水、平水、丰水年的发电量分别为602.83亿kWh,662.08亿kWh,699.17亿kWh,与天然径流的大小相对应,符合该流域梯级库群实际的调度结果的 [11] 。BSA算法在求解大规模梯级电站的长期调度问题时,不仅能够寻求到符合实际调度过程的全局最优值,而且寻求过程中的效率也是十分高的,从表2中可见三种典型年的求解耗时分别为26.61 s,25.17 s,24.66 s,在面对如此复杂的梯级库群调度问题求解,求解效率也完全能够满足电站时效性的需求 [12] 。因此,无论是在求解精度还是求解效率方面,BSA算法对于不同年份的梯级库群长期优化调度的求解都能够获得比较满意的结果,可以应用到电站的实际调度规划过程中 [14] 。

Table 3. Dispatching process in typical dry years
表3. 典型枯水年电站调度过程

Table 4. Dispatching process in typical normal water year
表4. 典型平水年电站调度过程


Table 5. Dispatching process in typical wet years
表5. 典型丰水年电站调度过程
 (a) 枯水年下梯级电站的出力过程
(a) 枯水年下梯级电站的出力过程  (b) 平水年下梯级电站的出力过程
(b) 平水年下梯级电站的出力过程  (c) 丰水年下梯级电站的出力过程
(c) 丰水年下梯级电站的出力过程  (d) 不同典型年下梯级库群的总发电量
(d) 不同典型年下梯级库群的总发电量
Figure 3. Output and power generation process of cascade reservoirs in different typical years
图3. 不同典型年下梯级库群的出力和发电过程
图2展示BSA算法优化下的各梯级电站在不同典型年下的水位、出力和发电量的变化过程,从图2的过程中可以看出,季调节电站A作为本次研究中梯级库群的龙头电站,在平时保持高水头来执行发电任务之外,还需在汛期前腾空库容再蓄水,充分发挥发电站的调节能力,确保枯期时下游电站的正常运行;年调节电站E,除了有大规模的发电机组,还有较好的调节性能,调度年份中,除了保持高水头进行发电外,在汛期,还会放掉一部分库容,对来水进行调节,保证枯期梯级库群的正常发电;季调节电站F作为电站E的下一级,有着充足的来水流量发电,电站G作为本次研究中该流域梯级库群中的最后一级电站,调节性能也一般,因此,它将水头蓄满后,将来水都用来发电,整个调度期内始终以高水头的情况进行发电 [3] [15] [16] [17] 。图3(a)~(c)为不同典型年下梯级库群在BSA算法优化下的各月出力过程,可以看出,在汛期,三种典型特征年下的梯级库群出力过程差别不大,但由于丰水年整体的天然径流量大,因此,在枯期的10、11、12月份,典型丰水年的出力是领先于平水年和枯水年的,是因为丰水年充分利用了天然径流的优势 [18] ,将多余的来水流量变成了梯级库群的发电量。图3(d)为不同典型年下梯级库群各月的总发电量 [19] ,整个发电量过程与不同典型年下的梯级库群出力过程类似,首先在汛期三种年份的发电量相差不大,然后由于梯级水电站能够较好地利用丰水年的多余来水,因此,对应调度期内的枯期10~12月的总发电量也最大,对应的月份发电量也最大。
5. 结论
本文以年发电量最大作为梯级库群的目标函数,考虑梯级库群之间的复杂约束和水力耦合现象,建立了梯级库群的长期优化调度模型,并采用的BSA优化算法进行优化求解。结合西南某流域的7座梯级电站为实际工程案例,证明了BSA算法优化效果十分可佳,整个调度过程中梯级库群各电站的出力和水位过程始终满足要求,同时又以较高的求解效率达到了模型的目标函数,使得整个梯级年发电量增加的同时,发电效率也有一定的提高,证明了BSA算法的有效性和实用性,为了梯级库群长期优化调度问题的求解提供了一种有效的方法。
参考文献