基于堆叠自编码网络与全连接层网络的手写数字识别算法的研究

Research on Handwritten Digit Recognition Algorithm Based on Stack Auto-Encoder Network and Full Connection Layer Network

摘要: 本文基于深度学习堆叠自编码网络与全连接层进行了手写数字的识别的算法研究，堆叠自编码神经网络能够挖掘数据内部信息，提取有效特征；全连接层进行分类预测。在MINIST数据集和大学生手写数字数据集中，与传统机器学习方法SVM及随机森林相比取得了更好的结果达到了0.967的准确率。本文设计的算法为堆叠自编码网络应用前景提供了研究基础。

Abstract: In this paper, the recognition algorithm of handwritten numerals is studied based on deep learning stack Auto-Encoder neural network and full connection layer. The Auto-Encoder neural network can mine the internal information of data and extract effective features; all connection layers are classified for prediction. Compared with traditional machine learning methods such as SVM and Random Forest, the MINIST dataset and college students’ handwritten digit dataset have achieved better results with an accuracy of 0.967. The algorithm designed in this paper provides a research basis for the application prospect of stacked Auto-Encoder neural networks.

1. 引言

深度学习在很多领域引起了广泛的关注，并在传统的识别任务中取得了不错的效果 [1] 。基于多个隐藏层，深度学习可以很好地实现复杂高维函数的表示，因此具有强大的表示能力 [2] [3] [4] ，并且具有其他算法没有的优点。堆叠自编码网络(SAE)是深度学习中最重要的模型之一 [5] ，可以从输入数据自动提取特征 [6] ，近几年，刘康等人并利用堆叠降噪自编码器(SDAE)解决数据噪声大、过拟合等问题，提高力学性能预测精度完成了航空发动机剩余寿命的预测 [7] ，李卫星等人实现发动机故障诊断与性能衰退评估 [8] ，潘蕾等人使用SAE网络提高化合物成药性预测的精准度 [9] 。以上例子说明了自编码网络算法在解决相关问题的能力，若能应用于生活之中，例如，如果能对学生的日常作业及试卷做出高质量的自动识别，做到线上自动批阅或者判分，那么将大大提高教师的工作效率和质量。因此本文构建了堆叠自编码网络与全连接层网络算法对手写数字识别进行实验讨论其可行性。

对手写数字识别问题，本文使用了基于堆叠自编码网络的无监督特征提取方法。它以自编码网络为基本单元，采用逐层贪心训练算法构建分层自编码网络模型，增强了网络的功能表达能力，使得网络模型可以从输入数据中自动提取特征来获得更好的效果，最后通过与softmax层连接实现对手写数字的识别。

本文分成三个部分，第一部分介绍网络模型与分析网络结构，第二部分进行手写数字识别实验并调参，第三部分与传统机器学习模型识别效果进行了比较。

2. 自编码神经网络

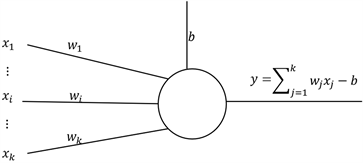
Figure 1. Schematic diagram of neuron structure

图1. 神经元结构示意

自编码神经网络是BP神经网络的一种特殊形式，基于若干神经元组成，如图1所示。自编码网络隐层神经元个数比输入输出节点数少，网络的输入数据与训练时输出数据的逼近目标都是同一组数据“见图2”。通过减小网络输出数据与目标数据的误差来训练模型。数据通过网络输入层经过降维把数据编码到维度更低的隐层(隐藏层)，从而去除数据中的冗余信息，提取能表征原始数据间关系的特征，再从隐层到输出层进行解码恢复到原始数据空间 [10] 。

Figure 2. Schematic diagram of the structure of the self-encoder neural network

图2. 自编码神经网络结构示意

编码函数定义为

$h=f_1\left(W^{\left(1\right)}\tilde{x}\right)+b^{\left(1\right)}$ (1)

式(1)， $f_1$ 表示编码激活函数， $W^{\left(1\right)}$ 表示连接输入层与隐含层的权重； $b^{\left(1\right)}$ 表示输入层的偏置项。解码函数定义为

$\hat{x}=f_2\left(W^{\left(2\right)}\tilde{x}\right)+b^{\left(2\right)}$ (2)

式(2)中， $f_2$ 表示解码激活函数， $W^{\left(2\right)}$ 表示连接隐含层与输出层的权重； $b^{\left(2\right)}$ 表示隐含层的偏置项。

由式(1)和式(2)可知，AE的输出 $\hat{x}$ 可表示为

$\hat{x}={\hat{h}}_{W,b}\left(x\right)=f_2\left\{W^{\left(2\right)}\left[f_1\left(W^{\left(1\right)}\tilde{x}\right)+b^{\left(1\right)}\right]\right\}+b^{\left(2\right)}$ (3)

(3)式中， ${\hat{h}}_{W,b}$ 为输入数据的重构函数。

对于一个含有m个样本的样本集 $\left\{x_1,x_2,\cdots ,x_m\right\}$ 采用的AE目标函数

$J\left(w,b;x\right)=\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\Vert h_{W,b}\left({\tilde{x}}_i\right)-x_i\Vert }^2}$ (4)

2.1. 深度自编码网络

深度自编码(DAE)网络是由多个浅层自编码网络(AE)或其变形网络堆叠而成，以上述AE作为基本结构单元，在编码器和解码器中增加隐层数量而构成。输入层和输出层的神经元个数相同，均为数据的维数。用编码器的输出作为新特征向量代替原始特征向量输入到解码器(回归模型)中，可以大幅度提高模型预测的准确度。本文DAE采用的目标函数为

$J\left(w,b;x\right)={\lambda }_1\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\Vert {\hat{h}}_{W,b}\left({\tilde{x}}_i\right)-x_i\Vert }^2}+{\lambda }_2\frac{1}{m}{\displaystyle \underset{i=1}{\overset{m}{\sum }}{\Vert h_{W,b}\left({\tilde{x}}_i\right)-x_i\Vert }^2}$ (5)

式中 ${\lambda }_1$ 和 ${\lambda }_2$ 分别为自编码和解码过程损失函数的权重系数， $h_{W,b}$ 为自编码网络输出。网络结构如图3。

Figure 3. DAE network structure diagram

图3. DAE网络结构图

2.2. 堆叠自编码网络

堆叠自编码网络(SAE)是由多层AE堆叠构成的层级深度神经网络，是一种基于逐层贪婪的无监督学习方法。SAE网络在预训练时第1层AE通过最小化重构误差将X维的原始输入数据映射到第1个含有 $n_1$ 个神经元的隐藏层，得到 $n_1$ 维的 $X^{\prime }$ ，即训练 $X-X^{\prime }-X$ 这个自编码器，训练结束后保留编码层的权重和偏差；以编码层得到的 $n_1$ 维的特征向量 $X^{\prime }$ 作为输入向量，再训练一个 $X^{\prime }-X^{″}-X^{\prime }$ 的自编码器，然后保留第2层AE的网络参数；以第2层AE编码得到的特征向量 $X^{\prime }$ 再作为下一层的输入向量，训练第3层的AE，……，以此类推，通过最小化输入和输出信号的重构误差来完成对输入数据的层层压缩，实现对输入数据的特征提取。通过这种方式，对整个SAE网络进行逐层预训练直到得到最后一个AE层，保存每一个AE的编码器参数，并将每个编码层串联起来形成预训练过的SAE模型，该SAE模型可以对化合物原始结构信息进行表征学习和降维。

3. 实验数据

本文使用MNIST数据集和大学生手写数字数据集 [11] ，MNIST数据集它是机器学习领域的一个经典数据集。MNIST每个样本都是一张28 × 28像素的灰度手写数字图片，且每个样本都对应着一个唯一的标签。大学生手写数字数据集的像素尺寸有差别，我们预处理过后让它的尺寸也为28 × 28像素。数据集包含60,000张训练图像和10,000张测试图像，本文使用10,000张图片做训练其中10%拿来做验证集，5000张MNIST和大学生手写数字数据集图片做预测验证。

4. 模型算法构建与训练

采用堆叠自编码器SAE算法，首先构建了特征提取网络；之后将具有10个神经元的分类器连接到SAE网络上，最终构成预测手写数字十分类网络，网络结构见图3。其中，隐藏层一共2层，第1层神经元数为100，第2层神经元节点数为50。详情见图4。

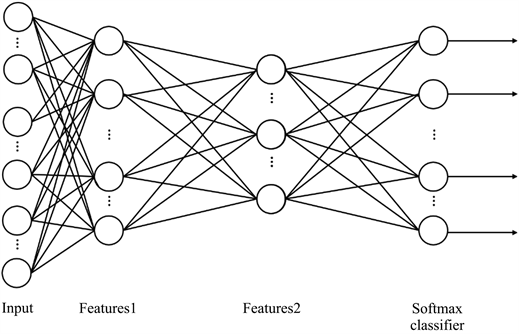
Figure 4. A schematic diagram of the model network structure

图4. 模型网络结构示意图

模型训练分为2步：第一，逐层对SAE特征提取网络进行训练；第二接入BP神经网络也就是(分类层)，将SAE训练得到的权重和偏差作为网络的初始化参数，并通过反向传播对整个网络进行微调，通过最小化目标变量的预测误差来获得改进的权重，直至模型稳定收敛。

模型训练过程包含了网络层数，节点数，激活函数，优化器，学习率以及batchsizes等，具体超参数设置如下表1。

Table 1. SAE hyperparameter setting table

表1. SAE超参数设置表

初始化函数使用默认产生正态分布随机数；特征提取网络共有2个隐藏层，节点数为100和50；在输入层使用0.1的防止过拟合；用sigmoid作为激活函数；Batchsize设为20；优化器采用Adam对模型进行训练并且学习率设置为0.001，利用梯度下降算法和梯度反向传播得参数进行更新，直至模型收敛。训练分类模型时，特征提取层使用SAE训练的参数值；分类层节点数设为10；激活函数采用分类函数softmax；损失函数设为crossentropy。

由图5可知，在20个epoch之前下降，在20个epoch之后训在一定范围内波动；在验证集中，二元交叉熵损失函数在20个epoch之前逐渐下降，在30个epoch之后在较小范围内波动趋近平稳；训练集上的准确率在20 epoch之前逐渐上升之后趋于平缓；验证集的准确率在20个epoch之前逐渐上升，20个epoch之后也趋于平缓。这说明此模型在第20个epoch时候收敛。

Figure 5. Training graph

图5. 训练图

5. 实验结果与分析

实验在测试集上准确率为0.967，与传统机器学习SVM准确率为0.902，随机森林准确率为0.932。可以看出SAE分类网络在手写数字识别上是优于传统机器学习方法的。具体表2如下。

Table 2. The comparison of the accuracy rate of the test set model

表2. 测试集模型正确率对比

6. 结束语

文中基于堆叠自编码神经网络与全连接层(softmax)结合进行了手写数字的识别。堆叠自编码神经网络是一种深度学习模型，它能够充分挖掘数据内部信息，提取有效特征，排除无关数据。此模型在MNIST数据集和大学生手写数字上取得了不错的效果，说明此方法的可行性。由于网络结构深度没有特别深，正确率只有相对高的0.967，若对网络结构进行调整与改进，网络参数进行优化相信其分类预测正确率会更高。这说明堆叠自编码神经网络与全连接层结合的深度学习网络算法应用到数字识别可行性，此外除了对数字的识别，此深度学习算法能通过微调网络结构等方式可用在其他领域。比如目标检测，异常识别等领域等。相信随着时间推移的和愈多的科研人员的努力，此算法能在更多领域发挥作用。