基于多元线性逐步回归的上海大学学生自习效率影响因素分析

Analysis of Influencing Factors of Self-Study Efficiency of Shanghai University Students Based on Multiple Linear Stepwise Regression

摘要: 进入大学之后，培养良好的自习习惯对大学生的学习效率有很大的关系，本论文以调查问卷的方式分析上海大学本科生乃至研究生学习效率与自习地点、自习时长等因素的相关性，通过引入虚拟变量，运用多元线性逐步回归分析的方法，建立学习效率与因素集之间的回归模型。结果表明，是否具有考研或者保研意向、自习时段、自习地点、非工作日自习时长对学习效率具有显著影响；同时经检验，模型的建立具有合理性。

Abstract: After entering the university, cultivating a good habit of self-study has a great impact on the learning efficiency of college students. This paper analyzes the correlation between the learning efficiency of undergraduate and graduate students in Shanghai University and the factors such as the location and length of self-study through questionnaires, and establishes a regression model between the learning efficiency and the factor set by introducing dummy variables and using the method of multiple stepwise linear regression analysis. The results show that the intention of postgraduate entrance examination or postgraduate retention, self-study period, self-study location and non-working hours have significant effects on learning efficiency; at the same time, through testing, the establishment of the model is reasonable.

1. 引言

大学生正处于人生发展的重要阶段，应不断进行自主学习以巩固拓展所学内容。如何拥有良好的学习效果是学生应该不断探索的问题。本实验旨在对学习效率的影响因素进行研究，并对大学生提出相关建议，具有一定现实意义。

石振阳等 [1] 采用回归分析、显著性检验的方法，通过问卷调查，以塔里木大学大学生为调查对象，探索影响大学生线上学习的各类因素，得出环境具有显著影响。李志河 [2] 依据情境学习理论和社会认知理论，采用相关分析和回归分析等量化研究方法，证明了学习主体、物理环境、数字技术和互动交流等四个方面是数字化场馆环境中非正式学习的主要影响因素。刘雪娇 [3] 等运用多项有序逻辑回归分析的方法根据学习情况分析预测大学生成绩等级，得出考研计划，听课认真程度，高考数学成绩是影响较大的因素。刘东 [4] 采用逐步回归分析和多元线性回归分析，根据赤峰市水资源使用情况预测分析该市全部城镇用水量。

在选择研究影响学习效果的因素上，相较于相关研究方向已有研究成果，本实验考虑的影响因素更加详细，包含的内容更加全面。在综合了自习地点(环境)、前往自习地点所需时间(路程)、自习时长、考研保研意向等常规因素外，创新性地将心情等其他因素纳入考虑范畴，并将自习时长进行“工作日”与“非工作日”的区别；对自习时段进行“上午”“下午”“晚上”“深夜”的细致划分。此外，考虑到不同年级、院系的绩点对应排名的差异性，本实验利用PCA (主成分分析法)将绩点和排名统一起来得到综合得分，同时作为衡量学习效率高低的标准。这使得实验结果更加严谨科学，也是本实验具有独创性的一步。

在数据处理过程与方法选择中，本实验利用SPSS软件进行数据分析与多元线性逐步回归。多元逐步分析法以线性回归为基础，其思路是将变量逐个引入，并在引入一个新变量后，对已入选回归模型的旧变量逐个进行检验，剔除低重要性、与其他变量高相关性的变量，重复操作直到没有新变量引入也没有旧变量删除，从而达到降低多重共线性程度的目的。相较于普通的多元线性回归，多元线性逐步回归由于增加了自变量筛选的这一步骤，可避免无统计学意义的自变量对回归方程的影响。使得自变量与因变量之间的关系得到更加准确的表达，具有更好的预测效果。

本实验以上海大学学生为调查对象，进行调查问卷的设计，回收有效问卷304份。

2. 问卷设计

2.1. 问卷指标设计

问卷共包含两个部分，第一部分对学生的一般信息进行了收集，第二部分为关于自习效率影响维度的指标信息的收集。本研究在结合既往 [5] 的自习影响指标的构建以及对上海大学学生的自习情况进行半结构化访谈，将可能影响自习效率的因素分为自习时间、自习环境、自身意愿三大维度以确立研究假设，各个维度下分几个指标。在本问卷的设计过程中，考虑到上海大学硬件设施和学生自身的相关情况，我们在指标设计中加入了该校具体的自习地点的选择情况，除常见的图书馆、宿舍等还加入了24小时学习空间和特定自习教室。其次针对该校选课自由的特点，对于自习时间的指标设计，除了常见的自习时长以外加入是否在上午、下午、晚上、深夜四个时间段自习的影响因素。此外还有对于自习学习效率的量化，由于不同专业类别的课程难易程度和老师给分习惯不一致，专业排名也是重要的影响因素，综合考虑以后我们使用这两个指标描述自习效率的高低，形成问卷。理论结构模型如图1所示。

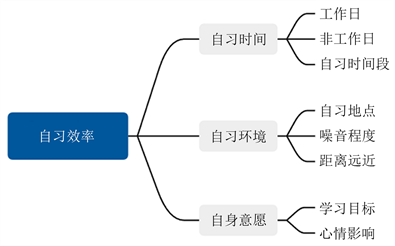
Figure 1. The index conception of the questionnaire influencing factors of self-study efficiency

图1. 自习效率影响因素问卷指标构想

2.2. 变量选择与定义

由于本研究要探究因变量自习效率与各个因素间的影响关系，而自习效率作为一种不可直接测量的潜变量，因而需要测量变量对其进行量化，本问卷选取了绩点以及专业排名作为测量变量，然后运用主成分分析法，对其进行降维度量，具体变量表示见表1。其中，Y₁代表该位学生的绩点，Y₂表示学生的专业排名，将二者进行主成分分析后得到的最终得分可以作为自习效率的测量。

Table 1. Dependent variable definition

表1. 因变量定义

在本问卷的设计过程中，考虑到学校的各种基础建设以及学生自身的相关情况，首先列出了可能影响学生自习效率的三个维度，分别为自习地点选取、自习时间以及学生的个人意愿，并对其赋予可测得的变量构建模型分析，表2对具体变量进行了详细定义。

Table 2. Argument definition

表2. 自变量定义

$X_i=0$ 或1 ( $i=1,2,3,4,5,10,13,14$ )， $X_i$ 分别代表是否在图书馆、24小时自习空间、自习教室、宿舍、其他地点、上午、下午、晚上、深夜自习以及是否具有考研或保研的意向，0表示否，1表示是； $X_i=1,2,3,4,5\left(i=6,7,15\right)$ ， $X_i$ 分别代表自习地点路程长短、自习地点噪音程度、心情好坏对学生自习效率的影响，1表示没有影响，2表示一般影响，3表示比较有影响，4表示很有影响，5表示非常有影响； $X_i=1,2,3,4,5\left(i=8,9\right)$ ， $X_i$ 分别代表工作日和非工作日每天的自习时长，1表示0~2小时之间，2表示2~4小时之间，3表示4~6之间，4表示6~8小时之间，5表示8小时以上。

下面随机抽取一个样本对变量进行举例说明。例如，我们选取一个性别为男，年级为大三，专业为理工类的样本对其进行解释。该同学通常进行自习的地点 $X_1=1$ ， $X_2=1$ ， $X_3=1$ ， $X_4=0$ ， $X_5=1$ ，说明该同学经常去图书馆、24小时自习空间、自习教室，宿舍和其他地点不会经常去；他认为自习地点噪音对其自习效率的影响程度 $X_6=3$ ，说明该同学对自习环境的声音要求较为严格；他认为自习地点路程长短对自习效率的影响程度 $X_7=1$ ，代表该学生认为路程长短基本不会影响自习效率；该同学工作日自习时长 $X_8=4~6$ 小时，非工作日自习时长 $X_9=6~8$ 小时；他通常自习的时段为 $X_{10}=1$ ， $X_{11}=1$ ， $X_{12}=1$ ， $X_{13}=0$ ，说明该同学通常自习的时段为上午、下午和晚上，而不在深夜自习；该同学考研情况为 $X_{14}=1$ ，则说明该同学拥有考研保研意向；他的心情为 $X_{15}=4$ ，则说明他认为心情对他的学习效率较有影响。

2.3. 问卷描述性统计

见表3，问卷的基本包括调查者的性别、年级和专业，题目共涉及自习地点、自习地点、前往自习地点所需时间、自习时长和专业等方面。

Table 3. Descriptive statistics

表3. 描述性统计

在确定了研究变量后，开始根据所求变量设计问卷问题。为避免出现实验结果只针对某一性别或某年龄对象而造成的特殊性情况，问卷首先对调查者的基本信息进行搜集，设置了性别和年龄的选择，便于实验员对问卷进行观察。为量化学习效果，本问卷将绩点分成数段供调查者选择。另外，为消除因不同专业造成的绩点差异的影响，问卷设计了专业与专业排名问题。问卷通过设计自习地点与噪音两道题目完成对于自习环境的描述；由于前往自习地点路程长短问题不易作答，因此将其替换成对前往自习地点所需时间的提问。最后对于自习时长和不同自习时间段进行统计，要求调查者从给出的时段中做出选择。

2.4. 数据采集结果

本问卷采用网上问卷以及线下发放问卷的形式进行调查，线上共发放260份问卷，线下共计发放70份问卷，得到线上245份有效问卷，线下59份有效问卷，最终共计304份有效问卷，有效回收率92.12%，调查样本具体信息见表4。

Table 4. Survey sample basic information table

表4. 调查样本基本信息表

3. 多元线性逐步回归的假设检验

进行多元线性回归分析时，需考虑四个假设：1) 因变量为连续型变量。2) 需要至少2个自变量，每个自变量和因变量在理论上有线性关系。3) 多个自变量不存在多重共线性。4) 残差要满足正态性、独立性、方差齐性。容易看出条件1)已经满足，下面分别对条件2~4是否满足进行检验。

本实验的相关变量可分为离散变量与连续变量。其中离散变量包括二分类变量与多分类变量，多分类变量包含有序变量(等级变量)和无序变量。例如：“综合得分”为连续变量；“考研(保研)意向”得到的结果为二分类结果，“自习地点”为无序变量；“自习时长”为等级变量。

3.1. 因变量和自变量线性分析判别

见表5，在各个自变量与因变量之间线性关系的探究中，对连续型和等级变量与因变量的线性关系进行验证。由ANOVO中F检验的显著性是否小于0.05判断得出：自习地点噪音影响和心情的影响与综合得分之间无明显线性关系，需要剔除。

Table 5. Linear test between independent variables and dependent variable

表5. 各自变量与因变量之间的线性检验

3.2. 多重共线性分析

见表6，容忍度均远大于0.1，方差膨胀因子均小于10，所以不存在多重共线性。

Table 6. Coefficients

表6. 系数

a. 因变量：自习效率。

3.3. 残差的正态性、独立性、方差齐性

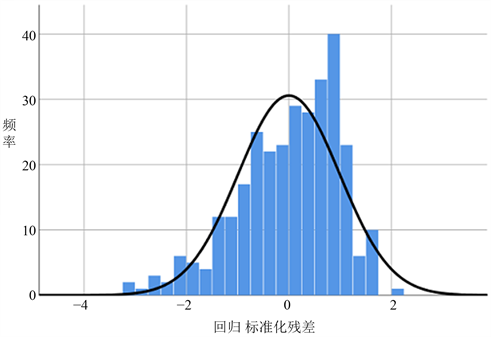
Figure 2. Regression normalized residual histogram

图2. 回归标准化残差直方图

从图2可以看出，本实验残差基本服从正态分布，均数接近于0，标准差接近于1，为标准正态分布，这表明此次实验线性回归满足正态性条件。

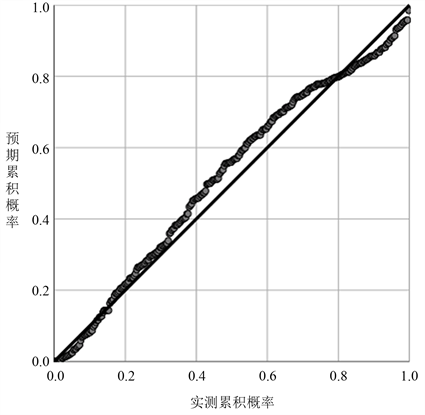
Figure 3. Normal P-P plots of regression standardized residuals

图3. 回归标准化残差的正态P-P图

图3反映的是实测累积概率与预期累积概率的关系，从图中可以看出，所有点均匀分布在一条直线两侧，同样也可证明残差具有正态性。

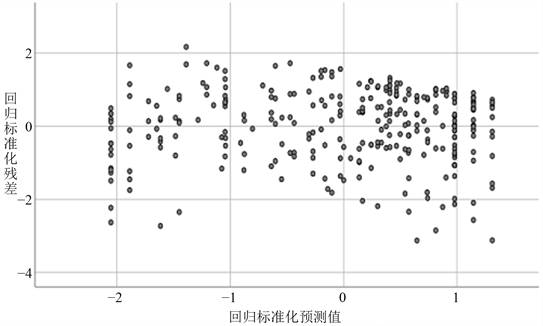
Figure 4. Scatter plot of regression standardized residuals

图4. 回归标准化残差的散点图

根据图4，回归标准化残差的散点图，可以看出残差的标准化值基本均匀地分布在0值周围，呈现上下对称随机分布，并且残差的分布特征不随预测值的增加而有其他趋势，可以认为数据满足方差齐性和独立性条件。

4. 多元线性逐步回归

见表7，多元线性逐步回归分析一共拟合了5个方程模型，输入方法为步进法。逐步回归分析中每一步建立多元线性回归方程引入的自变量依次为：考研意向、是否在上午自习、是否在自习教室自习、非工作日自习时长和是否在图书馆自习。

随着模型中变量个数的增加，R²和调整后R²均呈增加趋势；第五个多元线性回归模型即最终拟合模型的调整后R²接近0.3，表明最终模型中的五个自变量解释“自习效率”的接近30%的变异。德宾沃森检验若结果在0~4之间，基本可认为数据独立性符合。本例的德宾沃森值为1.676，符合独立性。

从该多元线性回归的最终模型的显著性检验中可以看出，F检验的结果 $F=26.631$ ，经过计算可得显著性小于0.001，可以说明多重线性回归模型中至少有一个自变量的系数不为零，则至少有一个自变量解释了一部分的因变量的变异，从而使得回归变异变大，残差变异减少，模型的建立有意义。同时，回归模型有统计学意义也说明其优于仅包含常数项的模型，纳入自变量有助于预测因变量。

Table 7. Stepwise regression analysis of comprehensive score and self-study factors

表7. 综合得分与自习因素的逐步回归分析

Y：自习效率；X₁₄：考研意向；X₁₀：在上午自习；X₃：在自习教室自习；X₉：非工作日自习时长；X₁：在图书馆自习。

表8显示：考研(保研)意向(0：无；1：有)、是否在上午自习、是否在自习教室、非工作日自习时长以及是否在图书馆均会明显影响学习效率，并且具有考研意向、在上午自习、在自习教室和图书馆自习以及非工作日自习时长越长，学习效率都会越高，这些因素均是正向影响学习效率(因为回归系数为正)。

由此我们可以对该结果进行解释：

1) 具有考研(保研)意向的同学，在自习活动中会具有更明确的目的性，能够更积极地进行自习，学习效率较之不具有该意向的同学明显提高；

2) 上午是一天中精力最充沛的时间段，能够在上午自习的同学通常能够有良好的作息习惯和自制力，起到正向影响自习效率的作用；

3) 自习教室以及图书馆相较于其他自习地点具有时间宽松、占座压力较轻、学习氛围良好等特点，能够养成在这两个地点自习的习惯对提升自习效率也具有一定的正向作用；

4) 相较于工作日有较多课程安排的非工作日，自习时间会相对来说较长，时间越长自习效率也相应越高；

5) 本文通过创新地使用多元逐步回归的方法，我们可以清楚细致地了解到问卷设问中影响程度较大的几个因素：考研(保研)意向、自习时间段与时长以及自习地点，所以同学们应该在培养自己良好的学习与作息习惯时注重这几点，教学主管部门也应该在前往自习地点的交通便利程度以及自习室开放时间、环境等方面给同学们提供便利。

Table 8. Regression coefficients

表8. 回归系数表

5. 结论

5.1. 结果分析

本论文通过设计发放调查问卷，收集了学生的基本信息、专业信息、自习地点、前往自习地点所需时间、自习时长、考研保研意向、学习心情以及绩点排名等信息。将绩点排名通过PCA方法进行降维，得到一个综合得分，作为因变量，将其余信息作为自变量，并通过引入虚拟变量将其量化为数据，进而使用多元线性逐步回归分析上海大学学生学习效率与因素集的相关性，并且根据结论给出相关建议。

多元线性逐步回归是在多元线性回归的基础上进行改进，只选取最重要的变量，通过将自变量逐步引入，建立模型，并在过程中除去显著性效果不理想的变量，最终建立最优多元线性方程，相较于多元线性回归效果更好，且避免了自变量过多的问题。

在具体实施过程中，本实验选择SPSS软件，首先对数据集进行线性分析判别，对数据的残差进行正态性、独立性和方差齐性分析，最终进行多重共线性验证，最终证明数据集适合使用多元线性逐步回归分析法。

通过上述多元线性逐步回归分析，结果显示，回归方程显著( $F=26.406,p<0.001$ )。其中，考研保研意向( $\beta =0.369,p<0.001$ )、是否在上午自习( $\beta =0.112,p=0.042$ )、是否在自习教室自习( $\beta =0.112,p=0.033$ )、非工作日自习时长( $\beta =0.119,p=0.023$ )、是否在图书馆自习( $\beta =0.117,p=0.025$ )这五个自变量的显著性 $p<0.05$ ，均显著正向预测学习效率。这些变量共解释学习效率29.7%的变异。而其余变量则因与学习效率无显著关系，因而无法确定其对学习效率产生较大影响。

5.2. 相关建议

针对上述结果，是否有考研和保研意向对学习效率是否高和学习成绩是否优秀有极大影响，是否在 非工作日时间保持足够长的学习时间、是否选择自习教室、图书馆等场所对学习效率和学习成绩都有一定影响。通常情况下，在上午学习的同学会有较高的学习效率，对学习成绩有一定的帮助。心情因素、前往自习地点的相关路程对学习成绩的影响相对不大。

因而，在同学们的日常学习过程中，可以给自己设定一个考研或保研目标，或是设定绩点排名目标等等，使自己有更明确的目的性，学习效率会有大幅提升。同时，学生应选择图书馆、自习室等适宜学习的场所，这对学习效率的提升也有正向影响；教学主管部门也可以多多开设自习教室，将空闲教室有效利用起来，为学生创造一个良好的学习环境。另外，同学们也要保证在非工作日有一个充足的学习时间，这对学习成绩的影响较大，但同时也要做到劳逸结合，否则会有负向影响。根据实验结论，上午是学习效率最高的时刻，选择在上午进行学习的同学普遍绩点和排名都较高，因而学生可以更多选择在上午进行自习。