基于生物信息学中DNA分子序列模式匹配算法研究实现

Research and Implementation of DNA Molecular Sequence Pattern Matching Algorithm Based on Bioinformatics

摘要: 生物信息学是融合先进的生物科学和计算机技术的一门综合运用数学、信息科学、计算机技术等对生物学、医学的信息进行科学的组织、整理和归纳的科学。DNA分子序列比对是生物信息学中最重要和最基础的研究方向之一，是探究基因与疾病关系的重要手段。本文研究的主要目标是在不确定的分子序列数据中找到所有与目标序列相同且出现概率大于给定阈值的序列，并给出目标序列总数及每个目标序列的起始位点。本文针对现有基于“空间换时间”的分子序列模式匹配算法仅限于次数的计算以及基于生物信息学中双DNA序列比对算法的图像立体匹配方法对于不确定的源数据具有局限性的问题，提出了一种基于加权后缀树的DNA分子序列模式匹配算法。该方法应用加权后缀树为主要数据结构，改进了不确定的源数据的匹配准确度，解决了map数据结构仅限于次数计算的问题，实验结果表明，本文提出的算法在匹配速度及灵敏度上有了一定的提高。

Abstract: Bioinformatics is a science that integrates advanced biological science and computer technology. It integrates mathematics, information science and computer technology to scientifically organize, sort out and conclude the information of biology and medicine. DNA sequence alignment is one of the most important and basic research directions in bioinformatics and an important means to explore the relationship between genes and diseases. The main objective of this paper is to find all sequences that are identical to the target sequence and whose occurrence probability is greater than the given threshold in the uncertain molecular sequence data and to give the total number of target sequences and the starting site of each target sequence. In this paper, a weighted suffix tree-based DNA sequence pattern matching algorithm is proposed to solve the problem that the existing molecular sequence pattern matching algorithm based on “space for time” is limited to the calculation of times, and the image stereo matching method based on the double DNA sequence alignment algorithm in bioinformatics is limited to uncertain source data. This method uses weighted suffix trees as the main data structure, improves the matching accuracy of uncertain source data, and solves the problem that map data structure is limited to number calculation. Experimental results show that the proposed algorithm has improved the matching speed and sensitivity to a certain extent.

1. 引言

生物信息学是融合先进的生物科学和计算机技术的一门综合运用数学、信息科学、计算机技术等对生物学、医学的信息进行科学的组织、整理和归纳的科学 [1] 。生物信息学的研究重点主要体现在基因组学和蛋白质学两方面，从核酸和蛋白质序列出发，分析序列中表达结构和功能的生物信息。近年来，随着高通量测序(NGS)技术的快速发展 [2] ，组学数据和表观遗传学数据呈指数增长 [3] ，海量的生物数据背后蕴含了大量的生物规律和知识。DNA/RNA甲基化修饰位点识别 [4] - [9] 、增强子识别 [10] [11] 、RNA序列编辑位点识别 [12] 、蛋白质功能位点识别 [13] 、DNA结合蛋白识别 [14] 等本质上都是多分类或二分类任务。DNA分子序列比对是生物信息学中最重要和最基础的研究方向之一，是探究基因与疾病关系的重要手段 [15] ，例如判断人体内是否存在致癌致病的关键DNA分子序列以及其存在的概率，通过概率大小判断是否需要提前介入性治疗等 [16] [17] 。

近年来，采用数据挖掘算法进行DNA分子序列模式匹配分析已成为生物信息学领域的研究热点 [18] [19] [20] 。目前基于DNA分子序列模式匹配研究的方法大致分为以下几类：一是，一种基于“空间换时间”的模式匹配算法 [21] ，以map数据结构来存储中间结果，使得扫描DNA序列一次即可同时计算所有元组模式在该序列中出现的次数。该算法通过分析DNA序列特征计算过程中的特殊性，提升了DNA序列模式特征计算的效率，但仅限于次数的计算，具有局限性。二是，一种基于生物信息学中双DNA序列比对算法的图像立体匹配方法，但此种算法对于不确定的源数据具有局限性。

基于此，本文针对现有基于“空间换时间”的分子序列模式匹配算法仅限于次数的计算以及基于生物信息学中双DNA序列比对算法的图像立体匹配方法对于不确定的源数据具有局限性的问题，提出了一种基于加权后缀树的DNA分子序列模式匹配算法。该方法应用加权后缀树为主要数据结构，保留了顺序遍历的优点，克服了无用序列遍历的缺点，改进了不确定的源数据的匹配准确度，解决了map数据结构仅限于次数计算的问题，在匹配速度及灵敏度上有了一定的提高。

2. 算法

DNA序列是由A (腺嘌吟碱基)、T (胸腺嘧啶碱基)、C (胞嘧啶碱基)、G (鸟嘌吟碱基) 4种碱基字符随意组合而成的字符串。在某些情况下，分子加权序列可以模拟调控蛋白结合位点的过程。由于DNA蛋白质复合物的特性，每个位置上个体碱基出现概率的总和与DNA蛋白质复合物的稳定性有关。如果总和大于给定范围，则DNA蛋白质复合物将被视为足够稳定的复合物。本文研究的主要目标是在不确定的分子序列数据中找到所有与目标序列P相同且出现概率大于给定阈值1/K的序列，并给出目标序列总数及每个目标序列的起始位点。由于后缀树是序列分析中重要且高效的数据结构 [22] ，因此本文选择后缀树和加权后缀树作为算法研究实现的主要数据结构。在处理分子加权序列时，需要找到给定范围内的所有目标序列，但是直接为文本中的每个位置构建后缀树会带来巨大的工作量，占用巨大的内存。由于不确定性和数据量巨大，为了提高效率，需要一定的阈值1/K，所有概率高于此阈值的对象将被保留。

2.1. 加权序列

加权序列 $X=X\left[1\right]\cdots X\left[n\right]$ 是一个位置序列，其中每个位置 $X\left[i\right]$ 由一组有序对 $\left(\sigma ,{\text{π}}_i\left(\sigma \right)\right)$ 组成， ${\text{π}}_i\left(\sigma \right)$ 是在位置i有字符σ的概率。对于每一个位置 $X\left[i\right]$ ，1 ≤ i ≤ n， ${\sum }_{\forall \sigma }{\text{π}}_i\left(\sigma \right)=1$ 。

例如，DNA分子序列字母表设为∑ = {A, C, G, T}，则图1中的加权序列可视为一串8个字母的字符串。位置1的字母可以是出现概率为0.4的A、出现概率为0.6的C；位置2、3、4、5的字母分别是T、T、G、C；位置6的字母可以是C、G、T，出现概率分别为0.2、0.1、0.7；位置7和8的字母分别为G和C。ω代表由一个或多个∑中字符组成的长度为n的序列。 $\omega \left[1\cdots n\right]=\omega \left[1\right],\omega \left[2\right],\cdots ,\omega \left[n\right]$ , $\omega \left[i\right]\in \sum$ , 1 ≤ i ≤ n。

Figure 1. An example of a weighted sequence with two weighted positions

图1. 具有两个加权位置的加权序列实例

由图1可以产生下列字符串：ω₁ = ATTGCCGC，ω₂ = ATTGCGGC，ω₃ = ATTGCTGC，ω₄ = CTTGCCGC，ω₅ = CTTGCGGC，ω₆ = CTTGCTGC，等等。从位置i开始的字符串ω的出现概率是每个字符出现概率的乘积。对于上述实例，我们可以得到：

$\begin{array}{l}\text{π}\left({\omega }_{\text{1}}\right)={\text{π}}_{\text{1}}\left(\text{A}\right)\ast {\text{π}}_{\text{2}}\left(\text{T}\right)\ast {\text{π}}_{\text{3}}\left(\text{T}\right)\ast {\text{π}}_{\text{4}}\left(\text{G}\right)\ast {\text{π}}_{\text{5}}\left(\text{C}\right)\ast {\text{π}}_{\text{6}}\left(\text{C}\right)\ast {\text{π}}_{\text{7}}\left(\text{G}\right)\ast {\text{π}}_{\text{8}}\left(\text{C}\right)=0.\text{4}\ast 0.\text{2}=0.0\text{8}\\ \text{π}\left({\omega }_{\text{2}}\right)={\text{π}}_{\text{1}}\left(\text{A}\right)\ast {\text{π}}_{\text{2}}\left(\text{T}\right)\ast {\text{π}}_{\text{3}}\left(\text{T}\right)\ast {\text{π}}_{\text{4}}\left(\text{G}\right)\ast {\text{π}}_{\text{5}}\left(\text{C}\right)\ast {\text{π}}_{\text{6}}\left(\text{G}\right)\ast {\text{π}}_{\text{7}}\left(\text{G}\right)\ast {\text{π}}_{\text{8}}\left(\text{C}\right)=0.\text{4}\ast 0.\text{1}=0.0\text{4}\\ \text{π}\left({\omega }_{\text{3}}\right)={\text{π}}_{\text{1}}\left(\text{A}\right)\ast {\text{π}}_{\text{2}}\left(\text{T}\right)\ast {\text{π}}_{\text{3}}\left(\text{T}\right)\ast {\text{π}}_{\text{4}}\left(\text{G}\right)\ast {\text{π}}_{\text{5}}\left(\text{C}\right)\ast {\text{π}}_{\text{6}}\left(\text{T}\right)\ast {\text{π}}_{\text{7}}\left(\text{G}\right)\ast {\text{π}}_{\text{8}}\left(\text{C}\right)=0.\text{4}\ast 0.\text{7}=0.\text{28}\\ \cdots \\ \text{π}\left({\omega }_{\text{i}}\right)={\text{π}}_{\text{1}}\left(\text{A}\right)\ast {\text{π}}_{\text{2}}\left(\text{T}\right)\ast {\text{π}}_{\text{3}}\left(\text{T}\right)\ast {\text{π}}_{\text{4}}\left(\text{G}\right)\ast {\text{π}}_{\text{5}}\left(\text{C}\right)\ast {\text{π}}_{\text{6}}\left(\text{A}\right)\ast {\text{π}}_{\text{7}}\left(\text{G}\right)\ast {\pi }_{\text{8}}\left(\text{C}\right)=0.\text{4}\ast 0=0\end{array}$

2.2. 后缀树

后缀树是一种重要的数据结构，对于处理字符串问题十分有效 [22] 。用 $T\left(\omega \right)$ 表示字符串ω的后缀树。设 $L\left(v\right)$ 表示 $T\left(\omega \right)$ 中从根到节点ν的路径标签。当 $L\left(v\right)=\omega \left[i\cdots n\right]$ 时， $T\left(\omega \right)$ 的叶节点ν被标记为i。将ν的叶列表 $LL\left(v\right)$ 定义为ν节点下面子树中的叶标签列表。后缀树支持ω上的快速精确字符串匹配：模式P从位置i开始出现当且仅当P是 ${\omega }_i$ 的前缀，则可以在 $\omega \left[i\cdots n\right]$ 中通过前缀搜索找到P的所有出现。由于字符串ω的最后一个字母为 $\$\notin \sum$ ，则没有一个后缀是另一个后缀的前缀，并且后缀树中的所有叶节点都是代表不同后缀的节点。示例：Let ω = banana$。如图2后缀树 $T\left(\omega \right)$ 所示，顶部节点是这个后缀树的根。节点0~6表示字符串ω的所有后缀。

节点0：banana$

节点1：anana$

节点2：nana$

节点3：ana$

节点4：na$

节点5：a$

节点6：$

Figure 2. Suffix tree T(ω)

图2. 后缀树T(ω)

2.3. 加权后缀树

加权后缀树是本算法使用的主要数据结构，用于存储具有一定出现概率的加权序列对应的后缀。由于这些属性，加权后缀树被认为是具有存在概率概念的广义后缀树。本文中使用加权后缀树Weighted Suffix Tree (WST)存储所有出现概率大于给定阈值1/K的目标后缀，然后求出给定模式P在可实现的最优时间内的所有出现次数及位点 [23] 。

X是一个加权序列，给从位置i开始的每个后缀定义一个可能的加权子字符串列表，并且每个后缀出现的概率大于给定阈值1/K。 $X_{i,j}$ 表示从位置i开始的后缀，j表示从位置i开始的第j个加权子字符串。 $WST\left(X\right)$ 表示加权序列X的加权后缀树。 $L\left(v\right)$ 代表 $WST\left(X\right)$ 中节点ν的路径标签。 $LL\left(v\right)$ 表示ν节点下面子树中的叶标签列表。为清楚地解释上述概念，举例找出 $X_{i,j}$ 中所有 $\text{π}\left(X_{i,j}\right)\ge 1/4$ 的分子序列，如图3所示。

1) $X\left[\text{1}\cdots \text{8}\right]$ 的前缀：

$X_{\text{1},\text{1}}=\text{<munder accentunder="true"> A <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{1},\text{1}}\right)=0.0\text{8};$

$X_{\text{1},\text{2}}=\text{<munder accentunder="true"> A <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{1},\text{2}}\right)=0.0\text{4};$

$X_{\text{1},\text{3}}=\text{<munder accentunder="true"> A <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{1},\text{3}}\right)=0.\text{28};$

$X_{\text{1},\text{4}}=\text{<munder accentunder="true"> C <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{1},\text{4}}\right)=0.\text{12};$

$X_{\text{1},\text{5}}=\text{<munder accentunder="true"> C <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{1},\text{5}}\right)=0.0\text{6};$

$X_{\text{1},\text{6}}=\text{<munder accentunder="true"> C <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{1},\text{6}}\right)=0.\text{42}.$

2) $X\left[\text{2}\cdots \text{8}\right]$ 的前缀：

$X_{\text{2},\text{1}}=\text{TTGC <munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{2},\text{1}}\right)=0.\text{2};$

$X_{\text{2},\text{2}}=\text{TTGC <munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{2},\text{2}}\right)=0.\text{1};$

$X_{\text{2},\text{3}}=\text{TTGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{2},\text{3}}\right)=0.\text{7}.$

3) $X\left[\text{3}\cdots \text{8}\right]$ 的前缀：

$X_{\text{3},\text{1}}=\text{TGC <munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{3},\text{1}}\right)=0.\text{2};$

$X_{\text{3},\text{2}}=\text{TGC <munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{3},\text{2}}\right)=0.\text{1};$

$X_{\text{3},\text{3}}=\text{TGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{3},\text{3}}\right)=0.\text{7}.$

4) $X\left[\text{4}\cdots \text{8}\right]$ 的前缀：

$X_{\text{4},\text{1}}=\text{GC <munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{4},\text{1}}\right)=0.\text{2};$

$X_{\text{4},\text{2}}=\text{GC <munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{4},\text{2}}\right)=0.\text{1};$

$X_{\text{4},\text{3}}=\text{GC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{4},\text{3}}\right)=0.\text{7}.$

5) $X\left[\text{5}\cdots \text{8}\right]$ 的前缀：

$X_{\text{5},\text{1}}=\text{C <munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{5},\text{1}}\right)=0.\text{2};$

$X_{\text{5},\text{2}}=\text{C <munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{5},\text{2}}\right)=0.\text{1};$

$X_{\text{5},\text{3}}=\text{C <munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{5},\text{3}}\right)=0.\text{7}.$

6) $X\left[\text{6}\cdots \text{8}\right]$ 的前缀：

$X_{\text{6},\text{1}}=\text{<munder accentunder="true"> C <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{6},\text{1}}\right)=0.\text{2};$

$X_{\text{6},\text{2}}=\text{<munder accentunder="true"> G <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{6},\text{2}}\right)=0.\text{1};$

$X_{\text{6},\text{3}}=\text{<munder accentunder="true"> T <mo> \_ </mo> </munder> GC},\text{π}\left(X_{\text{6},\text{3}}\right)=0.\text{7}.$

7) $X\left[\text{7}\cdots \text{8}\right]$ 的前缀：

$X_{\text{7},\text{1}}=\text{GC},\text{π}\left(X_{\text{7},\text{1}}\right)=\text{1};$

8) $X\left[\text{8}\right]$ 的前缀：

$X_{\text{8},\text{1}}=\text{C},\text{π}\left(X_{\text{8},\text{1}}\right)=\text{1};$

挑选出现概率大于等于1/4的序列：

$X_{\text{1},\text{3}}=\text{<munder accentunder="true"> A <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{1},\text{6}}=\text{<munder accentunder="true"> C <mo> \_ </mo> </munder> TTGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{2},\text{3}}=\text{TTGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{3},\text{3}}=\text{TGC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{4},\text{3}}=\text{GC <munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{5},\text{3}}=\text{C <munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{6},\text{3}}=\text{<munder accentunder="true"> T <mo> \_ </mo> </munder> GC}\$$

$X_{\text{7},\text{1}}=\text{GC}\$$

$X_{\text{8},\text{1}}=\text{C}\$$

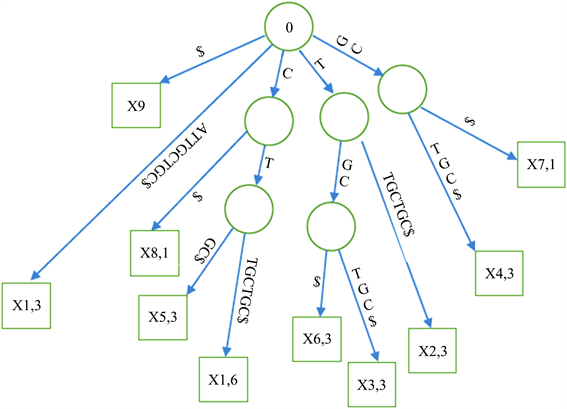
Figure 3. An example of a weighted suffix tree

图3. 加权后缀树实例

如前所述，为所有出现概率大于等于给定阈值1/K的子字符串建立加权后缀树是本算法的核心，有效地建立加权后缀树主要包括三个步骤：着色，生成和构造 [23] 。

2.4. 着色

对于给定的加权序列X，从左到右扫描每一个位置i，(1 ≤ i ≤ n)，并按如下规则求值：情况1：如果位置i所列的所有字母出现的概率都不大于阈值1-1/K，则位置i着色为黑色；情况2：如果存在一个字母，其出现在位置i的概率大于阈值1/K，则将位置i着色为灰色；情况3：如果位置i存在一个字母，其出现概率为1，则位置i着色为白色。

白色的位置因为只有一个字母出现的概率等于1，没有其他选择，因此被认为是足够稳定的位置；黑色的位置没有出现概率大于1-1/K的字母，而会有多于一个出现概率大于1/K的字母，因此将黑色的位置视为分支位置；对于灰色的位置，所有可能出现的字母出现的概率都小于1/K，只有一个特殊字母出现的概率大于1-1/K，这意味着最后只有一种选择。在着色阶段，为加权序列X的第一个位置以及所有黑色的位置生成一个队列B。同时创建一个向量COLOR来存储X的每个位置的颜色。示例：长度n = 10的加权序列X如表1所示。

Table 1. Weighted sequence X

表1. 加权序列X

设置阈值K = 4，1-1/K = 0.75。位置0有字母A的出现概率等于1，因此设置COLOR[0] = 0 (白色)。同理，位置1, 3, 5也是白色位置；位置2有一个概率为0.5的字母A和一个概率相同的字母C，没有一个概率大于1-1/K = 0.75或等于1。因此，设置COLOR[2] = 2 (黑色)。同理，位置4, 6, 8也是黑色位置；位置7有一个概率为0.2的字母A和一个概率为0.8的字母G，大于1-1/K = 0.75，因此设置COLOR[7] = 1 (灰色)。同理，位置9也是灰色位置。这样，可以得到完整的向量COLOR[ ] = {0, 0, 2, 0, 2, 2, 1, 2, 1}和队列B = {0, 2, 4, 6, 8}。

2.5. 生成

生成阶段的输入是加权序列X、队列B和来自着色阶段的向量COLOR。这一阶段的主要目的是生成存在概率大于1/K的所有子字符串。首先，从左到右扫描队列B中的每个位置，然后从每个黑色位置i开始生成若干可能的子字符串。具体的生成方法如下：第一，从黑色位置i开始，向右移动；第二，找到与前一个字符相同的单个字符，并将其添加到当前未完成的子字符串的末尾；第三，当遇到一个灰色或白色的位置时，意味着只有一个选择，继续添加它直到可以完成当前的子字符串；第四，尝试下一个可能的字母，并在这个黑色的位置创建一个新的子字符串，直到生成所有可能的子字符串；第五，从下一个黑色位置开始，重复以上步骤。该过程如图4所示。

Figure 4. The process of creating all possible substrings for the black position i

图4. 为黑色位置i创造所有可能的子字符串的过程

在这个阶段为每个生成的子字符串定义两个概率π'和π。π'存储的是真正的子字符串的概率，而π''存储的是将灰色位置视为白色位置时的概率。当满足以下条件时，生成过程停止：首先，当第一次遇到一个黑色位置并且π''已经小于1/K，记录下来；其次，如果所记录位置的下一个位置为黑色，则停止生成，并将所记录的位置标记为扩展位置。否则，如果从所记录的位置开始的下一个位置是白色或灰色位置，只需将白色或灰色的位置相加，直到再次遇到黑色的位置，最后一个白色或灰色的位置标记为扩展位置，如图5所示。由于π'可能提前满足阈值1/K，则实际子字符串可能比扩展子字符串短，因此定义了每个产生子字符串的真实结束位置与扩展结束位置之间的距离差D。

Figure 5. Extended substring Z' and actual substring Z

图5. 扩展子字符串Z'及实际子字符串Z

示例：使用加权序列X (见表1)、向量COLOR[ ] ={0, 0, 2, 0, 2, 2, 1, 2, 1}和着色阶段产生的队列B = {0, 2, 4, 6, 8}来生成因子。首先，从左到右扫描队列B，得到第一个位置0。其次，为0号位置创建空的树，从0号位置开始扩展子字符串(如图6树0所示)。将所有的树(分别见图6~9和图10)添加到队列LT中，将在构造阶段使用。

Figure 6. Tree 0

图6. 树0

Figure 7. Tree 2

图7. 树2

Figure 8. Tree 4

图8. 树4

Figure 9. Tree 6

图9. 树6

Figure 10. Tree 8

图10. 树8

2.6. 构造

从每个黑色位置生成所有可能的子字符串后，在广义后缀树中插入每个扩展子字符串，然后从树中删除扩展字符。示例：使用加权序列X (见表1)、着色阶段生成的向量COLOR[] = {0, 0, 2, 0, 2, 1, 2, 1}和生成阶段生成的队列LT来构建后缀树。首先，从左向右扫描队列LT，可以得到树0 (如图6所示)。其次，对于每个树中的所有叶子，得到每个叶子的Z'路径标签，并将Z'插入加权后缀树中，同时插入Z'的后缀，并计算相应的Dj，如表2所示。继续插入子字符串并删除冗余部分，直到所有树的所有叶子都被检查完毕，最后我们可以得到完整的加权后缀树，如图11所示。

Table 2. Construction process of tree 0

表2. 树0的构造过程

Figure 11. A complete weighted suffix tree

图11. 完整的加权后缀树

3. 结果与分析

根据影响实验运行时间及结果的三个因素：模式P，阈值K和不同长度的测试文件进行多组测试。测试数据文件：text2k.fa，text20k.fa，text50k.fa，text100k.fa，text150k.fa，text200k.fa。分别取文本长度2000、20,000、50,000、100,000、150,000、200,000，选取K = 2、K = 4、K = 6、K = 8、模式P长度等于2、4、8、16、32进行一系列测试。部分实验结果见表3。

Table 3. Experimental results

表3. 实验结果

基于阈值为4的K，测试不同长度的模式P和不同长度的测试数据。从表4可以看出，当阈值K固定时，模式P的长度对运行时间影响不大，而测试数据长度对运行时间影响较大。

Table 4. K = 4

表4. K = 4

基于长度为8的模式P，测试不同阈值K和不同长度的测试数据。从表5可以看出，当模式P长度固定时，阈值K和测试数据长度都对运行时间有一定的影响。

Table 5. The length of pattern P is 8

表5. 模式P长度 = 8

基于长度为100 k的测试数据，测试不同阈值K和不同长度的模式P。从表6可以看出，当测试数据长度固定时，模式P长度对运行时间影响不大，而阈值K对运行时间影响较大。

Table 6. The length of test data is 100 k

表6. 测试数据长度 = 100 k

综上所述，当阈值K越来越大时，黑色点位会越来越多，需要建立更多后缀树，该算法的运行时间主要与阈值K正相关。从实验结果可以看出，相较于常规的Map-Based算法和双DNA序列比对算法的图像立体匹配方法，本文提出的算法在模式较为复杂的情况下，匹配速度及不确定数据的位点精准度上表现优异，这主要是因为Map-Based算法比较适用于模式比较简单、长度较短情况下单个序列的模式计算，在数据位点定位上存在较大缺陷。在进行算法匹配前，本文提出的算法仅需要对源数据进行处理，而Map-Based算法需要对模式及源数据都进行预处理，此过程要进行m × n次，m、n分别为序列数集和模式数集，此过程进行的辅助数据的重复计算会给模式匹配的性能带来很大的损失，预处理消耗的时间远大于加速时间。

本文提出的基于加权后缀树的模式匹配算法在应用到DNA分子序列特征计算时，能很好地应对DNA序列数目庞大、单个DNA序列的长度较长的情况，并精确地定位发生位点的位置，解决了仅能进行次数计算的缺点。实验结果表明，在实际应用中该算法不仅效率更高而且匹配精准度及性能稳定性更高，并且易于实现，具有一定的应用推广价值，对探究基因序列知识具有重要意义。

基金项目

廊坊市科技支撑计划项目(2020011045)，北华航天工业学院科研基金项目(KY-2020-16)，北华航天工业学院研究生创新资助项目(YKY-2021-20)。