一种改进的多尺度多特征立体匹配算法

Improved Stereo Matching Algorithm Based on Multi-Scale and Multi-Feature

摘要: 在双目立体视觉领域中，立体匹配是其重要研究方向。为了针对部分立体匹配算法在弱纹理区域有较高的误匹配率的问题，本文提出一种基于多尺度多特征的立体匹配算法。将STAD、梯度与改进后的Census代价融合作为代价计算方法，代价聚合阶段，以引导图滤波算法为核心，利用跨尺度的思想将不同尺度的代价立方体进行融合，其中对于不同尺度的代价立方体设置了不同的代价聚合参数。对于视差图结果的一些错误，采用了多种视差后处理的方法。实验结果表明了该算法在弱纹理区域的准确性，对Middlebury3.0测试平台上标准图像对的实验结果表明，该算法在多组弱纹理图像上的平均误匹配率为8.16%，较传统的SGM等算法有更高的匹配精度。

Abstract: In the field of binocular stereo vision, stereo matching is an important research direction. In order to solve the problem that some stereo matching algorithms have high error matching rate in the weak texture region, this paper proposes a stereo matching algorithm based on multi-scale and multi feature. The STAD, gradient and improved Census cost fusion are used as the cost computing method. In the cost aggregation stage, take the guided filtering algorithm as the core. The cost cubes of different scales are fused using the idea of cross scales, and different cost aggregation parameters are set for the cost cubes of different scales. For some errors in disparity map results, a variety of methods of disparity post-processing are used. The experimental results show the accuracy of the algorithm in the weak texture area. The experimental results of standard image pairs on the Mid-dlebury 3.0 test platform show that the average mismatch rate of the algorithm in multiple groups of weak texture images is 8.16%, which has higher matching accuracy than the traditional SGM and other algorithms.

1. 引言

立体匹配算法在计算机视觉中是研究难点 [1] ，立体匹配算法性能的评价标准一般认为是匹配准确率和算法运行时间。现如今由于GPU足够强大，即使是很复杂的图像，立体匹配算法也能够利用其并行计算的能力很快计算出结果，例如CostFilter [2] 和Plane-FitBP [3] ，他们都几乎能做到实时计算。故而只要算法的核心技术能够进行并行加速，例如引导图滤波算法 [4] ，算法的运行时间就显得不是那么重要，因此人们更为关注算法的准确率，并由此开始研究立体匹配的难点：镜面反射；遮挡；重复纹理、弱纹理甚至无纹理等情况。

纹理具有区域性和尺度性的特点，弱纹理一般指一个区域局部属性是单一的，例如：白墙、桌子。尺度，这种生物灵感往往容易被许多优秀的算法所忽视，所以本文算法基于多尺度去研究弱纹理区域。

Scharstein [5] 等将立体匹配技术总结成四步：代价计算、代价聚合、视差计算、视差后处理。在代价计算阶段，对于每个像素所有可能视差的范围内计算匹配代价进而形成一个代价立方体。在代价聚合阶段，代价被聚合，以一种算法将像素邻域的代价进行聚合来增强局部的视差一致性。最后计算出视差并且根据各种各样的视差后处理技术来优化视差。

在这四个步骤中，每个步骤都对算法的成功性至关重要，针对弱纹理区域而言，不同的代价计算方法获得的结果完全不同。而代价聚合阶段是很多优秀算法的核心 [6] [7] ，对结果影响非常大。因此，本文主要关注代价计算和代价聚合两个阶段。

很多代价聚合方法都用到滤波技术方框滤波和高斯滤波，这会导致深度边界模糊 [8] 。直到K He等 [4] 提出引导图滤波算法，对图像边缘的保留效果非常好的同时算法运行速度远远低于双边滤波 [9] ，而且还可以在图像平滑处使用，是目前最快的边缘保留过滤器算法。

由于引导图滤波算法突出的效果和极快的速度，基于引导图滤波算法的立体匹配方法引起了广泛的关注。Tan P等 [10] 将引导图滤波算法用于局部立体匹配算法的代价聚合阶段，依赖于引导图滤波算法的自适应参数。在没有立体匹配困难的图像对(没有镜面反射和弱纹理)上获得了不错的效果，代价计算简单并且实验并没有考虑弱纹理图像。Hosni等 [11] 也将引导图滤波算法用于立体匹配上，但其本身的代价计算阶段只是简单的应用截断的颜色强度代价和梯度代价的融合，针对处理弱纹理图像稳定性更强的Census代价并没有涉及到。当立体匹配算法在图像存在大量弱纹理区域的时候，算法失效的问题显得尤为突出。

近年来，卷积神经网络(convolutional neural networks, CNN)在计算机视觉领域风靡全球，吸引了众多学者将其应用于立体匹配问题中，建立了诸如GC-Net (geometry and context network) [12] 、PSM-Net (pyramid stereo matching network) [13] 、GA-Net (guided aggregation network) [14] 等神经网络模型的立体匹配方法，在各大数据集上一直有着较高的排名。但是这些神经网络的方法需要经过数据集的训练，对于数据集的规模和质量都要很高的要求，而且对于场景的泛化性较差。

上述现有方法首先都只是考虑一个尺度，没有考虑利用多尺度图像，在代价计算时利用的特征也不够多，并且只是简单的将引导图滤波算法应用于立体匹配阶段，完全没有考虑图像的弱纹理区域，对于强、弱纹理是统一的处理方式，这存在一定的局限性，其算法在图像的弱纹理区域的匹配精度表现较差。而深度学习存在着容易受到数据集限制、人工成本、泛化性等的问题。因此本文提出一种多尺度多特征的方法，针对纹理是在尺度下观察的特点，应用高斯金字塔形成多尺度图像，在代价计算阶段融合多种特征，并且在代价聚合阶段，根据多尺度的特点设置不同的算法参数进行代价聚合，而后融合多种不同尺度的代价立方体保证算法既能在普通场景又能在弱纹理场景拥有不俗的表现，在视差后处理阶段，使用多种优化方法使得算法对于弱纹理区域有较高的稳定性以求得平均误匹配率较低的视差图。保证了算法在图像拥有大量弱纹理区域时的有效性，同时避免了人工标注大量样本的成本问题和复杂的网络结构设计问题。

2. 算法描述

根据Scharstein [5] 对于立体匹配系统的阐述，本文算法更为详细的对其进行增加，主要由生成高斯金字塔图像对、匹配代价计算、代价聚合、融合多尺度代价、视差计算、视差后处理六步，按照顺序前后依进行，算法流程如图1所示。

Figure 1. Algorithm flowchart

图1. 算法流程图

2.1. 代价计算

相比于基于特征点的方法，基于区域的代价函数往往是更优的选择，传统的基于区域的代价计算方法包括：单一的AD代价、AD代价与Census代价融合、AD代价与梯度代价融合、归一化互相关(NCC) [15] 等几种方案。

本文提出的代价计算方法，由于Census变换 [16] 在立体匹配算法中表现非常好 [17] ，因此，在代价计算阶段将STAD代价与梯度代价融合后的代价与改进后的Census代价进行融合加大Census变换的权重。

Census变换是一种非参数的局部变换，核心思想是设置一个方形的窗口，将窗口内每个像素的灰度值与中心像素的灰度值进行比较得到一串布尔值形成一个比特串如图2所示。

Figure 2. Census transformation

图2. Census变换

以上就是Census变换，而基于Census的代价计算的方法是计算左右两图之间像素对应的Census变换值之间的汉明距离，也就是：

$\begin{array}{c}{C}_0\left(u,v,d\right):=\text{Hamming}\left(C_{SR}\left(u,v\right),C_{ST}\left(u-d,v\right)\right)\end{array}$ (1)

其中， $C_{SR}\left(u,v\right)$ 为左图像像素点 $\left(u,v\right)$ 的Census变换， $C_{ST}\left(u-d,v\right)$ 为右图像像素点 $\left(u-d,v\right)$ 的Census变换， $C_0\left(u,v,d\right)$ 就是所求像素点的Census代价。

在实际应用中，由于图像可能会受到光照、噪声等的影响引起像素突变，当中心像素由72突变成60的时候，如图3所示。

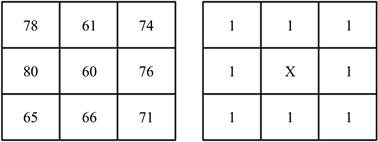
Figure 3. Census transformation after sudden change of center pixel

图3. 中心像素突变后的Census变换

我们可以看到只要窗口内中心像素的值突变，比特串的值从10110001变成了11111111，变化非常大，这对于误差是很明显的。

针对Census变换后的比特串而对于传统Census变换过于依赖窗口内中心像素的问题，本文改进Census变换。由于邻域像素的灰度是近似的，首先计算出窗口内的像素灰度的平均值，接着将窗口内的像素灰度值与此平均值作差并设置一个阈值，只要差值大于这个阈值，那么则令窗口内的中心像素值等于窗口内像素平均值。

窗口内中心像素突变后，Census变换改进后如图4所示，本文设置的阈值为9，求取中心值等于70.1，大于9，因此将60替换成70.1，替换后的比特值为10111001，可以看到当窗口内中心像素突变的时候，改进后的Census变换具有一定的稳定性。

传统的基于STAD和梯度融合的代价计算函数可表示为

$C_{STAD}\left(u,v,d\right)=\frac{1}{3}\underset{x\in S,C\in \left\{R,G,B\right\}}{{\displaystyle \sum }}\min \left\{\left|I_R\left(u,v\right)-I_T\left(u-d,v\right)\right|,T\right\}$ (2)

$C_{SG}\left(u,v,d\right)=\underset{x\in S}{{\displaystyle \sum }}\min \left\{\left|\begin{array}{c}{\nabla }_x{I}_R\left(u,v\right)-{\nabla }_x{I}_T\left(u-d,v\right)\end{array}\right|,T\right\}$ (3)

$C_1\left(u,v,d\right)=\left(1-\alpha \right)\cdot C_{SG}\left(u,v,d\right)+\alpha \cdot C_{STAD}\left(u,v,d\right)$ (4)

其中 $\alpha$ 权重系数， $C_{STAD}\left(u,v,d\right)$ 是STAD代价， $C_{SG}\left(u,v,d\right)$ 是梯度代价， $C_1\left(u,v,d\right)$ 是融合后的代价， 为截断阈值。

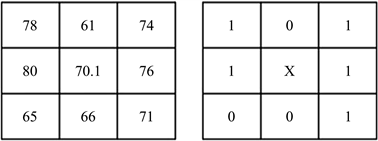
Figure 4. Improved census transformation

图4. 改进后的census变换

本文采用自然指数函数将代价取值的结果归一化到[0, 1]之间，总的代价计算函数如下：

$C\left(u,v,d\right)=2-\exp \left(-\frac{C_1\left(u,v,d\right)}{{\lambda }_1}\right)-\exp \left(-\frac{C_0\left(u,v,d\right)}{{\lambda }_0}\right)$ (5)

其中，c是匹配代价的值， $\lambda$ 是加权系数。在代价计算中，本文算法参数包含梯度代价与STAD代价融合的权重 $\alpha$ 、Census与上述代价融合的权重 ${\lambda }_0$ 、 ${\lambda }_1$ 以及代价计算中一般固定的截断阈值T和改进后Census的阈值。

(a) Cones (b) 本文算法(c) 梯度-Census (d) AD-Census

Figure 5. Comparison of cost compute disparity results in weak texture regions

图5. 代价计算视差结果在弱纹理区域的对比

三种代价中，Census代价保证弱纹理区域能有较好的匹配能力，STAD代价来确保在重复纹理区域有较好的匹配能力和对颜色的敏感性，加入梯度代价能保证留存一定的边缘信息，对深度不连续区域的匹配精度有一定的保证。三种代价计算的方式进行融合，能够取长补短，提升算法的鲁棒性。

为了验证这种多特征融合的有效性，本文从Middlebury数据集挑选一组弱纹理图像，将由梯度-Census、AD-Census、本文算法三种代价计算方式获得的视差图结果列举如图5所示，视差图结果由WTA (WinnerTake All)策略和视差后处理优化获得。从弱纹理区域可以看出，梯度-Census代价明显无法处理大面积的弱纹理区域，AD-Census代价减少了弱纹理区域的错误率，但是不如本文代价计算方法在弱纹理区域的有效性并且总体错误率更高。

2.2. 代价聚合

代价聚合的根本目的是减少或者消除错误代价的影响。局部代价聚合的思路是以一定的准则对代价立方体进行优化，根据相邻像素在同一视差或相邻视差的代价值来重新计算某一像素点在某个视差下的代价值。Zhang等 [18] 在多尺度空间下应用引导图滤波代价聚合方法，并引入正则项来加强不同尺度空间之间的联系。

本文采用上述方法，对于引导图滤波算法而言，其参数参包含正则化参数 $ϵ$ ，实现算法过程中窗口大小参数 $r_2$ ，其中 $ϵ$ 越大滤波后的图像越平滑， $ϵ$ 越小滤波后的图像保留的越完整，大窗口包含更多的信息但同时缺失一定的细节。弱纹理常需要大窗口来包含更多的图像信息并且需要更平滑的图像，由于本文是在多尺度的基础上完成的，因此本文对于不同尺度下的代价立方体设置不同的代价聚合算法参数进行计算，均衡包含不同尺度下的信息，在保证拥有较为完整边缘的情况下同时在弱纹理有较高的精度。

为了加强不同尺度间的联系，在引导滤波模型后面添加正则项 [18]

$B_s\left(z\right)=\lambda {\Vert z^s-z^{s-1}\Vert }_2^2$ (6)

式中， $\lambda$ 为正则化因子， $s$ 为尺度空间的序数， $z^s$ 为对应尺度空间上对应像素的代价值。 $\lambda$ 取值越大，说明算法对同一像素点在不同尺度空间下的一致性约束越强，能够进一步增大算法对弱纹理区域的视差估计、提高算法的鲁棒性。采用一种多尺度间代价聚合后自适应结合的方法获得最优的代价立方体。

由两种代价聚合方法经过WTA策略获得的视差图如图6所示，可以明显感受到在图像的弱纹理区域，改善后的跨尺度代价聚合方法比原始的误匹配率低，更好的还原了深度不连续区域的视差，图案下方也能更好地还原弱纹理区域的视差值。本文在引入尺度代价融合的基础上进一步在不同尺度上选择不同的参数进行代价聚合然后融合，取得了更为可观的效果。

(a) 原始 (b) 改善后

Figure 6. Original cross scale cost aggregation results and improved cross scale cost aggregation results

图6. 原始的跨尺度代价聚合结果与改善后的跨尺度代价聚合结果

2.3. 视差计算与视差后处理

最为普遍的视差计算策略是胜者为王策略，具体计算方法如下

$D\left(u,v\right)=\arg \min C\left(u,v,d\right)\left(d\in \left[0,d_{\max }\right]\right)$ (7)

其中 $D\left(u,v\right)$ 为像素坐标为 $\left(u,v\right)$ 时的视差， $C\left(u,v,d\right)$ 为代价计算或者代价聚合后的代价立方体中像素坐标为 $\left(u,v\right)$ 视差为d时的代价，d位于视差搜索范围 $\left[0,d_{\max }\right]$ 。

由于遮挡等非立体匹配算法能处理的因素，由视差计算获得的视差图错误的匹配点或者不能匹配的区域，这就需要进行视差后处理来优化视差图。

本文首先对视差图进行左右一致性检测来剔除异常点，随后进行视差填充，也就是给无效点像素分配一个有效值，虽然经过左右一致性检测和视差填充能够对视差图有一个较好的优化，但是视差图中可能存在随机噪声及非连续的错误匹配点，尤其是在深度不连续和弱纹理区域，视差图的平滑性很差，因此最后对视差图进行加权中值滤波的处理来平滑视差图。本文算法计算流程示意图如图7所示，多尺度下的每个图像对都要进行代价计算与代价聚合，其中不同尺度的代价聚合算法参数不同，所有尺度计算完后进行尺度间的代价立方体融合，最后进行视差计算和视差后处理得到最终视差图，和标准视差图对比，感官上本文算法与其比较接近。

Figure 7. Flow diagram of algorithm

图7. 算法流程示意图

3. 实验结果分析

为验证本文算法在弱纹理区域的有效性，将本文算法与经典的SGM算法、由Hao Liu等提出的改进的经典AD-Census的ADSG [19] 在Middlebury3.0 [20] [21] 平台上挑选两组弱纹理图像和一组常规图像进行实验对比，对三种算法都使用此评估平台的十五组标准图像的Q版本(原始尺寸的1/4大小)作为实验对象来验证本文算法的有效性以及在能够在弱纹理区域较多的图像上有一定的鲁棒性。实验中的阈值设为1，也即将实验得到的结果与标准视差图作对比，只要误差超过一个像素，即认为此点为误匹配点。

本文算法主要的实验参数如表1所示，其中括号表示不同尺度间的引导图滤波算法参数设置。

Table 1. Main parameter settings of algorithm

表1. 算法主要参数设置

从十五组图像挑选出三种代表性的图像进行展示，分别是常规图像Teddy、重复纹理极多的Shelves图像、弱纹理图像Playtable。分别对图像的非遮挡区(Non-occlusion, Nonocc)和所有区域计算出误匹配率，部分实验结果如下表2所示：

Table 2. Comparison of mismatch rate of three algorithms

表2. 三种算法的误匹配率对比

从表中实验结果可以看出本文算法在采用针对弱纹理图像的算法参数上，在常规图像上与其它两种算法有一定的差距，但是根据实验证明，通过对本文算法的参数进行调整可以到达同等水平，同时本文算法在图像存在大量弱纹理区域时的实验结果远超于另外两种算法。

为了增强实验的可靠性，从十五组图像中挑选出两组弱纹理图像Vintage、Playtabel进行定性分析，经由本文算法得到的视差图如图8、图9所示。

暖色表示更大的视差和更小的深度，从图8中可以看到本文算法对比于SGM算法整体上更接近与标准视差图，视差图质量更高，像在计算机、键盘、桌面等弱纹理区域的表现远远优于SGM。

从图9中可以看出相比于SGM算法，本文算法空洞更少，在像桌子、椅子等弱纹理部分质量更好，且在深度不连续区域(例如桌子腿)也有较好的效果。整体上看本文算法所获的Playtabel图像对的视差图质量胜过SGM算法。

(a) (b) (c) (d)

Figure 8. Vintage: (a) left image; (b) standard disparity; (c) disparity of stereo matching in this paper; (d) disparity of stereo matching by SGM

图8. Vintage：(a) 左图；(b) 标准视差图；(c) 本文立体匹配算法得到的视差图；(d) SGM立体匹配算法得到的视差图

(a) (b) (c) (d)

Figure 9. Playtabel: (a) left image; (b) standard disparity; (c) disparity of stereo matching in this paper; (d) disparity of stereo matching by SGM

图9. Playtabel：(a) 左图；(b) 标准视差图；(c) 本文立体匹配算法得到的视差图；(d) SGM立体匹配算法得到的视差图

在Middlebury3.0上，对于存在大量弱纹理区域的Vintage图像，在非遮挡区域上，SGM算法平均误匹配率为13.8%，本文算法平均误匹配率为7.28%，较传统算法有所降低。对于Playtabel图像，在非遮挡区域上，SGM算法平均误匹配率为15.72%，本文算法平均误匹配率为9.04%，较传统算法有所降低。两组弱纹理图像的平均误匹配率为8.16%，通过视差图质量对比和平均误匹配率对比证明了本文算法的整体有效性且在弱纹理区域上也有良好的表现。

4. 结束语

本文提出一种基于不同尺度下的多种特征融合的引导图滤波的立体匹配算法。由于传统Census变换对窗口中心点的依赖性较大，本文对其进行改进，将中心像素与其窗口内其他像素的均值作差值，并设置阈值，根据情况对中心像素值进行替换，来保证算法的稳定性。并且针对不同尺度下的图像选择不同的引导图滤波算法的参数，经过代价聚合后得到多尺度的代价立方体，通过引入正则项来加强不同尺度间的联系，从而整体提高算法在弱纹理区域的匹配精度。融合不同尺度下的代价立方体经过视差计算和后处理最终获得视差图。实验结果表明，相较于传统SGM算法，本文算法能够较好地适应不同纹理图像对立体匹配的影响，能够在弱纹理区域拥有更高的精度。

NOTES

^*通讯作者。