统计过程控制在网络销售中的应用

The Application of Statistical Process Control in Network Sales

摘要: 现有网络销售的研究中，人们非常关心订货量，订货周期，销售价格和利润等变量。从统计过程控制的角度，给出了监控网络销售变量参数变化的一般框架。鉴于网络销售变量分布的多样性，建立了多元的Max-EWMA控制图用来监控网络销售变量的均值向量的漂移。通过蒙特卡洛模拟比较了Max-EWMA控制图与MEWMA控制图和T²控制图的性能。以马氏距离度量漂移的大小，以AR(1)模型刻画变量间的相关性。模拟结果表明，Max-EWMA 控制图对监控中小漂移比较有效，具有较理想的性能。

Abstract: In the existing research of online sales, people are very concerned about the variables such as order quantity, order cycle, sales price and profit. From the perspective of statistical process control, a general framework for monitoring the change of network sales variable parameters is given. In view of the diversity of the distribution of online sales variables, a multivariate Max-EWMA control chart is established to monitor the drift of the mean vector of online sales variables. The performances of Max-EWMA control chart, MEWMA control chart and T² control chart are compared by Monte Carlo simulation. Mahalanobis distance is used to measure the drift, and AR(1) model is used to describe the correlation between variables. The simulation results show that the Max-EWMA control chart is effective in monitoring small and medium drift, and has better performance.

1. 引言

伴随着信息科技的发展与创新，网络销售应运而生。现在的网络销售问题，日益引起学者们的关注，从不同的视角展开研究。一方面，研究其特点、发展趋势及影响因素。陈金平(2022)论述了我国电子商务发展的特点和趋势 [1] 。戴先红(2022)分析了特色农产品网络营销发展的影响因素 [2] 。张函弛和张幸福(2023)分析了疫情时代对餐饮业网络销售的影响 [3] 。另一方面，进行预测、数学建模及数据分析。王斌等(2020)利用ARIMA模型对网络销售的订单进行了预测 [4] 。王长琼等(2021)研究了新零售供应链的订货模型及策略 [5] 。吴宇平和李磊(2022)研究了网络销售数据的稀疏性问题 [6] 。以上文献从宏观的角度论述了网络销售的特点及发展趋势，也从统计分析的角度进行了预测及数据分析。

在进行统计分析时，所得出的统计结论严重依赖于某些变量或统计量的分布以及所使用的概率或统计模型。当变量或模型的参数发生变化时可能会使得之前所得出的统计结论不再成立，甚至会是相反的结果。因此，在网络销售的应用研究中，判断参数、分布或模型是否发生变化是非常有必要的。可以借助于统计过程控制(Statistical Process Control, SPC)中的控制图来解决这个问题。SPC是保证产品或服务符合规定要求的一种质量管理技术，它包含一些用来降低产品质量波动以使产品质量保持稳定的诸多有效工具。朱建平等(2023)展示了统计学研究的10个重要发展方向 [7] 。在网络产品的质量和生产率统计方法及应用研究中，网络产品的统计过程控制研究是重要的一部分。

综上，本文从另一个视角研究网络销售问题，研究SPC在网络销售中的应用，仅给出监控网络销售变量参数是否变化的一般框架。在网络销售的研究中，所关注的变量往往是多元的，包括订货量、订货周期、销售价格等等。因此需要建立多元的控制图对网络销售的过程进行监控。多元控制图的研究成果已非常丰富，包括多元Shewhart形式的、累积和(Cumulative Sum, CUSUM)形式的、指数加权滑动平均(Exponentially Weighted Moving Average, EWMA)形式的，还包括多元非参数的控制图。Sanusi等(2020)建立了二元的Max-EWMA控制图用来监控伽马和指数分布的数据 [8] 。鉴于网络销售变量分布的多样性(订货周期是两次订单的间隔时间，其分布是指数的；订货量是正态的)，本文把Sanusi等的Max-EWMA控制图推广到多元的情况，然后用来监控网络销售的过程。通过蒙特卡洛模拟，Max-EWMA控制图具有较好的表现。

2. Max-EWMA控制图

在网络销售问题中，人们通常关注订货量、订货周期、利润、销售价格等多个变量。这里，不妨假设有p元的网络销售指标 $\tilde{X}=\left(X_1,X_2,\cdots ,X_p\right)$ 。假设网络销售指标 $\tilde{X}$ 的协方差矩阵 $\Sigma$ 保持稳定不变。假设在某个未知时刻 $\tau$ 之后， $\tilde{X}$ 的均值向量由 $\tau$ 时刻之前的 ${\mu }_0$ 变为 ${\mu }_1$ (称为发生了漂移)。我们的目标是对网络销售过程进行监控，利用控制图来检测测量值分布的任何漂移。

记监控时刻为t，t时的样本为 $\left(X_{1t},X_{2t},\cdots ,X_{pt}\right)$ ，通过Max-EWMA控制图进行监控的过程如下：

首先计算EWMA序列

$M_{1t}={\lambda }_1{X}_{1t}+\left(1-{\lambda }_1\right)M_{1t-1},\cdots ,M_{pt}={\lambda }_p{X}_{pt}+\left(1-{\lambda }_p\right)M_{pt-1},t=1,2,\cdots ,$ (1)

其中 $M_{10}=M_{p0}=0$ ，而 ${\lambda }_1,\cdots ,{\lambda }_p\in \left(0,1\right)$ 称为光滑参数。

然后计算Max-EWMA序列 $\left\{Z_t\right\}$ ，即

$Z_t=\text{Max}\left(\left|M_{1t}\right|,\cdots ,\left|M_{pt}\right|\right)$ . (2)

当监控统计量 $Z_t>h$ 时，Max-EWMA控制图发出销售过程失控的警报。h称为控制线，通常使用二分法经蒙特卡洛随机模拟得到。

在线监控的流程图如图1所示。

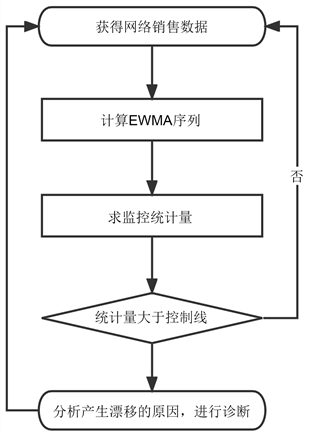
Figure 1. Flow chart of monitoring process

图1. 监控过程的流程图

研究结果表明，当光滑参数 $\lambda$ 取比较小的数值时，EWMA类型的控制图对小漂移更有效；当 $\lambda$ 取比较大的数值时，EWMA类型的控制图对比较大的漂移更有效 [9] 。一般建议 $\lambda$ 取0.05，0.1或0.2。如果想兼顾不同大小的漂移，可以建立自适应的多元EWMA控制图 [10] 或自适应的多元CUSUM控制图 [11] 。

3. 统计模拟

通过统计模拟将Max-EWMA控制图与MEWMA控制图 [12] 和Shewhart形式的T²控制图 [9] 进行性能比较。本节后面的所有结果都基于10,000次模拟。为简单起见，假设所关心的网络销售指标是p元正态的。尽管对样本作了正态性假设，事实上根据中心极限定理，即使样本偏离正态假设，3个控制图的结果仍然是近似可以用的。假设过程受控时，网络销售指标的均值向量是零向量，协方差矩阵满足AR(1)相关，即

$\mathrm{cov}\left(X_i,X_j\right)=\{\begin{array}{l}{\rho }^{\left|j-i\right|},i\ne j\\ 1,i=j\end{array},$

这里 $\left|\rho \right|<1$ 。后面模拟时， $\rho$ 被选为0.5和0.8两种情况。

在受控时的平均运行长度(ARL，记为ARL₀)相同或相近的情况下，比较不同控制图的过程失控时的ARL (记为ARL₁)。哪个控制图的ARL₁越小，其在过程失控时报警越早，因此表现越好。为了比较的公平，Max-EWMA控制图与MEWMA控制图的光滑参数 $\lambda$ 都取为0.05，调整3个控制图的控制线使其ARL₀接近370。分 $p=5,\rho =0.5$ (Scenario1)和 $p=20,\rho =0.8$ (Scenario2)两种情况，模拟的控制线见表1。

Table 1. Simulated h values of different charts

表1. 模拟的三个控制图的控制线h

通过马氏距离 $d=\sqrt{{\left({\mu }_1-{\mu }_0\right)}^{\prime }{\Sigma }^{-1}\left({\mu }_1-{\mu }_0\right)}$ 来度量均值向量漂移的大小 [13] ，其中 ${\mu }_0$ 是过程受控时的

均值向量( ${\mu }_0=0$ )， ${\mu }_1$ 是过程失控时的均值向量(假定漂移大小d后，由d算得)。这里， ${\mu }_1$ 取 $\delta 1$ 的简单形式， $\delta$ 是一个常数， $1$ 是都为1的向量。表2给出了 $p=5,\rho =0.5$ 时各控制图的ARL。 $d=0$ 时表示过程是受控的，其对应的ARL即为ARL₀，其它情况对应的ARL是ARL₁。由表2可以看出，Max-EWMA控制图对监控中小漂移比较有效，而T²控制图对监控大漂移比较有效。例如， $d=0.3$ 时，Max-EWMA控制图的ARL₁为76.92，而T²控制图的ARL₁为320.5； $d=5$ 时，T²控制图的ARL₁为1.13，而Max-EWMA控制图的ARL₁为3.16。可见，对中小漂移，Max-EWMA控制图能较早地报警；对大漂移，T²控制图能较早地报警。

Table 2. Comparisons of ARL when p = 5 , ρ = 0.5

表2. $p=5,\rho =0.5$ 时，ARL的比较结果

表3给出了 $p=20,\rho =0.8$ 时各控制图的ARL，与表2所得出的结论类似。因此，在监控网络销售的p元指标时，如果关心的是中小漂移可以建立Max-EWMA控制图，如果关心的是大漂移可以建立T²控制图。进一步，如果数据的分布未知，想要建立稳健的控制图，可以参考多元的非参数控制图 [14] 。如果只对某一侧的漂移感兴趣，可以参考多元的单边控制图 [15] 。

Table 3. Comparisons of ARL when p = 20 , ρ = 0.8

表3. $p=20,\rho =0.8$ 时，ARL的比较结果

为了便于理解控制图的使用，图2给出了一个模拟的监控示例。在 $p=5,\rho =0.5$ 的情况下，随机模拟了50个样本，前5个样本是受控的，后45个样本是在d取0.5的情况下产生的。计算各控制图在不同监控时刻对应的监控统计量，画出散点图，用虚线连接，并用虚线在对应的图上分别画出每个控制图的控制线。从图2可以很直观地看出，Max-EWMA控制图与MEWMA控制图发出了过程失控的警报，而T²控制图没有发现漂移。

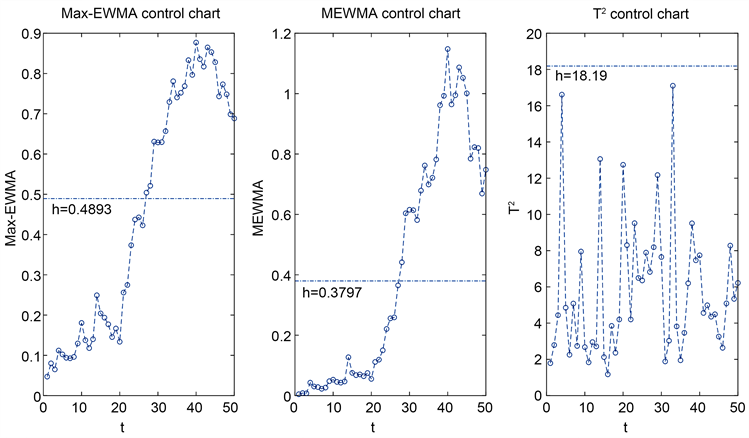
Figure 2. The Max-EWMA, MEWMA and T² control charts for the simulated data

图2. 三个控制图的监控示例

4. 结论

提出了通过统计过程控制对网络销售中的订货量、订货周期、利润、销售价格等多变量进行在线监控的理论框架。建立了Max-EWMA控制图对网络销售过程进行监控，利用该控制图来检测测量值分布的任何漂移。统计模拟表明该控制图对监控中小漂移有良好的表现。为了帮助我们适当地调整销售过程，还需要检测到底是哪个测量分量发生了漂移，这称为诊断，可以参考Zou等2011年的工作 [16] 。

基金项目

吉林省教育厅项目(JJKH20210809KJ)、国家自然科学基金面上项目(12271271)。

NOTES

^*通讯作者。