基于改进NSGA-II的柔性工艺路线多目标优化

Multi-Objective Optimization of Flexible Process Route Based on Improved NSGA-II

摘要: 针对机械零件加工的柔性工艺路线规划的低碳高效多目标优化问题，根据零件加工过程碳排放和完工时间的影响因素，建立了以最少碳排放和最短完工时间为目标的工艺路线优化模型。采用三段式编码方式对柔性工艺路线进行描述，为了提高算法的局部搜索能力，将成绩标量函数值作为评价标准，采用模拟退火操作以改进NSGA-II (Non-dominated sorting genetic algorithm II)进行优化求解；同时将约束矩阵引入算法中，保证生成的工艺路线满足特征约束。以某型号导向轴支撑座的加工工艺为例，验证了所提模型和优化方法的可行性和有效性。结果表明，所提改进算法与传统NSGA-II算法相比，平均排放量和完工时间分别降低了4.3%和3.6%，该研究可对工艺路线的低碳高效多目标优化问题提供一定的参考。

Abstract: Aiming at the low carbon and high efficiency multi-objective optimization problem of flexible pro-cess route planning for mechanical parts processing, a process route optimization model aiming at the minimum carbon emission and the shortest completion time is established according to the factors affecting the carbon emission and completion time of the parts processing process. Three segment coding method is used to describe the flexible process route. In order to improve the local search ability of the algorithm, the score scalar function value is used as the evaluation standard, and simulated annealing operation is used to improve NSGA-II (Non dominated sorting genetic al-gorithm II) to optimize the solution; At the same time, the constraint matrix is introduced into the algorithm to ensure that the generated routing meets the feature constraints. Taking the machining process of a certain type of guide shaft support as an example, the feasibility and effectiveness of the proposed model and optimization method are verified. The results show that compared with the traditional NSGA-II algorithm, the average emissions and completion time of the improved algo-rithm are reduced by 4.3% and 3.6%, respectively. This study can provide some reference for the low-carbon and high-efficiency multi-objective optimization of process routes.

1. 引言

加工工艺路线规划是零件机械加工过程中最为重要的环节，对零件的加工效率、加工能耗、工艺成本等企业经营目标具有重大影响 [1] 。工艺路线的柔性表现在加工方法、加工资源及加工顺序的多样性，造成工艺路线的不唯一，因此工艺路线规划优化问题是一个非线性、多目标的NP-hard组合优化问题。目前，针对加工成本、加工质量、加工效率等工艺规划的传统优化指标，国内外已开展一系列研究 [2] [3] [4] [5] 。近年来全球变暖问题日趋严峻，而制造业作为高能耗、高排放的行业，是温室气体的主要来源之一，因此越来越多的学者将低碳排放融入机械加工工艺路线规划的优化目标中。

李聪波等 [1] 建立了以总碳排放最低和总加工时间最短为优化目标的多目标优化模型，以某电动机座为例，通过遗传算法进行寻优求解得到其优化的工艺路线，并将多目标优化与单目标优化结果进行对比，结果验证了多目标优化算法的有效性；张雷等 [6] 分析了箱体类零件的加工成本和碳排放影响因素，采用多色集理论建立了围道布尔矩阵描述工步的排序问题，通过改进的遗传算法对低碳低成本目标进行了优化；Liu等 [7] 提出了工艺规划与车间调度的集成优化模型，同时考虑两者对车间能耗的影响并引入非支配排序遗传算法(Non-dominated sorting genetic algorithm-II, NSGA-II)进行低碳优化，实现了工艺规划与车间调度的共同优化；Zhou等 [8] 提出一种量化零件工艺路线碳排放的评价模型，综合考虑碳排放、加工时间和成本为优化目标，采用改进的多目标蚁群算法获得了最优工艺路线，并通过轴承座实例验证了模型和算法的有效性。上述研究成果均以最小碳排放为目标对工艺路线进行了优化，但随着低碳需求的日益凸显，且加工特征间约束关系复杂导致不可行解比例大，需采用更加高效的寻优求解方式，扩大可行解空间以找到更加真实准确的解集。

基于此，本文在零件机加工过程的碳排放与时间影响因素分析及量化研究的基础上，建立低碳和高效目标的数学优化模型，提出一种改进的NSGA-II算法对优化模型进行多目标优化求解。使用模拟退火操作提高NSGA-II算法的局部搜索能力，避免陷入局部最优解，扩大可行解空间；同时融入特征约束矩阵以对加工元的加工顺序进行可行性检验及修正。通过实例验证本文所提优化方案的可行性和有效性，证明本文的研究有助于降低机加工柔性工艺路线的加工能耗及提高其加工效率。

2. 柔性工艺路线优化模型

2.1. 条件假设

本文工艺路线规划的目标，是在多种可行的工艺路线中选出一条，使得碳排放最小和加工时间最短。为了简化问题以便于研究，本文作如下假设：

1) 本文考虑的零件加工工艺，是指毛坯件经热处理工艺完成后的机加工阶段，主要包括车削、铣削、钻削等机加工工艺，不考虑热处理和毛胚工艺；

2) 零件的加工工序顺序必须遵循特征顺序约束原则；

3) 一道工序加工完成后，若涉及转换机床，忽略搬运能耗和搬运时间。

2.2. 优化问题描述

工艺路线规划问题是一个复杂的组合优化问题，为了便于描述该问题，本文将加工零件的N个加工特征表示为一个特征集合：

$F=\left\{F_1,F_2,\cdots ,F_I,\cdots ,F_N\right\}$ (1)

每个加工特征由一个或若干个加工工步组成的加工链进行加工，每个加工工步定义为一个加工元。如某个特征面的加工方法为加工链：“粗车—半精车—精车”，则其包含3个加工元。零件所有加工特征的加工方法组成的加工路线Pro表示为各特征加工元的集合：

$Pro=\left\{pr{o}_{1,1},pr{o}_{1,2},\cdots ,pr{o}_{I,J},\cdots ,pr{o}_{N,M}\right\}$ (2)

其中：pro_I,J为特征I的第J个特征元，M为特征N的第M个加工工步。

由于后续主要以加工元作为核心的研究单位，故将加工元集合简化为：

$Pro=\left\{pr{o}_1,pr{o}_2,\cdots ,pr{o}_i,\cdots ,pr{o}_n\right\}$ (3)

其中：n为零件所有加工元的总数，pro_i为加工元i，具体表示为式(4)：

$pr{o}_i=\left\{U_i,M_i,T_i\right\}$ (4)

其中：U_i为加工元编号，M_i为加工机床编号，T_i为加工刀具编号。

综上所述，加工工艺路线优化问题可描述为：对于一个待加工零件，为给定加工元集合Pro中的每个加工元pro_i确定其加工机床M_i、刀具T_i，并将集合中所有加工元进行顺序排列，使所形成的工艺路线在满足加工特征顺序约束的前提下，达到加工过程碳排放量最小和加工时间最短的优化目标，以实现机械零件加工的更低碳、更高效。

2.3. 多目标优化模型

2.3.1. 约束条件

设零件所有特征的加工元集合Pro中有n个元素，若按照排列组合计算，有n!种排列方式。但由于加工特征之间存在客观约束，合理可行的加工路线数目远小于n!。加工特征间的合理性约束主要有先粗后精、先主后辅、基准先行和不破坏原则等，特征之间的约束信息形成加工元之间的约束关系。零件n个加工元间的约束关系可用n阶的约束矩阵R = [R_xy]_n×n来表示 [9] ，R_xy表示加工元x与加工元y之间的约束关系，当R_xy = 1，R_yx = 0时，表示加工元x优先于加工元y；当R_xy = R_yx = 0时，表示两个加工元间不存在约束关系。

2.3.2. 优化目标函数的建立

1) 低碳目标函数

加工工艺路线规划的低碳目标体现在零件从毛坯件到成品的机加工工艺过程产生的温室气体量最小，由于温室气体中二氧化碳对全球变暖影响最大，本文以二氧化碳为折算基准。零件加工过程中的碳排放主要包括机床能耗所产生的直接碳排放和刀具损耗及切削液消耗产生的间接碳排放。

a) 机床能耗排放

对于每道加工元，选择不同的机床，其对应的加工时间、加工功率各不相同，直接影响零件加工过程中机床能耗，本文将机床加工过程的碳排放按机床运行阶段进行计算。

机床待机阶段主要由于零件加工前的准备工作，包括工件装夹、刀具更换等，待机阶段的碳排放计算公式可用式(5)表示：

$C{E}_{\text{s}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}E{F}_{\text{e}}\cdot P_{\text{s},k}\cdot t_{\text{s}}\left(pr{o}_i\right)/\left(3.6\times {10}^3\right)}$ (5)

其中：EF_e为电能碳排放因子，根据国家生态环境部2022年发布的《关于做好2022年企业温室气体排放报告管理相关重点工作的通知》明确，当前全国平均电能碳排放因子为0.5810 g CO₂/(w∙h)；P_s,k为加工元i对应的加工机床k的待机功率，w；t_s(pro_i)为加工元i加工机床k的待机时间，s。

机床空载运行主要由于加工过程中的进退刀，空载过程碳排放计算方法可用式(6)表示：

$C{E}_{\text{u}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}E{F}_{\text{e}}\cdot P_{\text{u},k}\cdot t_{\text{u}}\left(pr{o}_i\right)/\left(3.6\times {10}^3\right)}$ (6)

其中：P_u,k为机床k的空载功率，t_u(pro_i)为加工元i加工机床k的空载时间。

刀具从工件上切除多于材料的过程即切削加工阶段，切削过程机床能耗由材料去除能耗与切削过程中负载运行产生的额外附加载荷能耗组成，其碳排放计算公式如式(7)~(9)：

$C{E}_{\text{c}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}E{F}_{\text{e}}\cdot P_{\text{c}}{}_{,k}\cdot t_{\text{c}}\left(pr{o}_i\right)/\left(3.6\times {10}^3\right)}$ (7)

$P_c=P_r+P_a$ (8)

$P_a=\alpha \cdot P_r$ (9)

其中：P_c,k为加工元i的加工机床k切削加工的功率，由材料去除功率P_r和附加损耗功率P_a组成；t_c(pro_i)为零件加工元i的切削时间；附加载荷损耗的机理非常复杂，文献 [10] 指出损耗功率和切削功率可表示为如式(9)所示的正比例关系，其中α为附加载荷损耗系数。

b) 刀具磨损碳排放

不同刀具的使用寿命和质量不同，零件加工过程中的刀具磨损碳排放量也就不同。刀具磨损碳排放为刀具的制备能耗产生的碳排放，可按加工时间折算到加工过程中，其计算方法如式(10)：

$C{E}_t={\displaystyle \underset{i=1}{\overset{n}{\sum }}E{F}_t\cdot \frac{t_c\left(pr{o}_i\right)}{T_t}}\cdot W_t$ (10)

其中：EF_t为刀具碳排放因子，由文献 [6] 可知其值为30.153 g CO₂/g；T_t为刀具t的寿命，s；W_t为刀具t的质量，g。

c) 切削液碳排放

切削液碳排放为零件加工时所用的切削液的制备碳排放和废弃处理碳排放，与切削加工时间和切削液更换周期有关，其计算方法如式(11)：

$C{E}_f={\displaystyle \underset{i=1}{\overset{n}{\sum }}\frac{t_c\left(pr{o}_i\right)}{H_i}\cdot \left(E{F}_p+E{F}_h\right)\cdot C}$ (11)

其中：H_i为加工元i所用切削液的更换周期，一般为两到三个月；EF_p、EF_h分别为切削液制备碳排放因子和废弃处理碳排放因子，由文献 [11] 可得分别为2.85 g CO₂/mL和0.2 g CO₂/mL；C为切削液用量，mL。

综上分析，零件加工工艺路线的总碳排放优化目标函数为式(12)：

$\min CE=C{E}_{\text{s}}+C{E}_{\text{u}}+C{E}_{\text{c}}+C{E}_{\text{t}}+C{E}_{\text{f}}$ (12)

2) 高效目标函数

加工工艺路线规划的高效目标体现为零件机加工过程的总完工时间最短。总完工时间由工件所有加工元的加工总时间和机床转换时间组成。

a) 加工阶段时间

选择不同的加工资源，会造成加工元不同的加工时间。零件加工阶段时间为所有加工元的加工时间总和，包括零件加工时的机床待机时间、机床空载时间和切削加工时间：

$T_{\text{c}}={\displaystyle \underset{i=1}{\overset{n}{\sum }}t\left(pr{o}_i\right)}$ (13)

$t\left(pr{o}_i\right)=t_s\left(pr{o}_i\right)+t_u\left(pr{o}_i\right)+t_c\left(pr{o}_i\right)$ (14)

其中：t(pro_i)为加工元i的加工时间。

b) 机床转换时间

机床转换时间指的是相邻两个加工元之间需要在不同的机床上进行而产生的工件拆卸和重新装夹的时间。前后两道加工元的加工机床选择，直接影响零件的拆卸、装夹以及换刀次数，从而影响零件的总完工时间。以t_m(pro_i)表示加工元的机床更换时间，则零件工艺路线总的机床转换时间计算方法为式(15)：

$T_m={\displaystyle \underset{i=1}{\overset{n}{\sum }}{t}_m\left(pr{o}_i\right)\cdot S_m}$ (15)

其中：t_m(pro_i)为加工元i的机床转换时间，S_m为加工元i是否需要转换机床的决策变量，若需要则等于1，否则等于0。

综上所述，零件加工工艺路线的总完工时间优化目标函数为式(16)：

$\min T=T_c+T_m$ (16)

3. 多目标优化求解

目前，NSGA-II [12] 是被应用的最为广泛的一种快速的多目标进化算法。该算法在基本遗传算法的基础上，引入非支配排序、拥挤度和精英策略，达到降低算法复杂度、保证种群多样性和提高计算效率的目的 [13] 。但该算法存在局部搜索能力较弱、后期搜索速度缓慢的缺陷 [14] ，因此本文提出一种改进的NSGA-II算法。该算法在染色体进行遗传操作后融入模拟退火算法操作，通过成绩标量函数(Achievement scalarizing function, ASF) [15] 作Metropolis接受准则的判断标准，使算法陷入局部极值时有机会跳出寻优；并引入基于约束矩阵的约束检验与修正方法，对个体进行可行性检验及修正，保证个体的有效性。

3.1. 编码与解码

本文采用实数编码方式，每个染色体包括三层编码结构，代表零件加工的一条完整的工艺路线。某个体染色体如图1所示，包括加工元编号子串U_x、加工机床编号子串M_x及加工刀具编号子串T_x。U_x中的每个基因代表每个加工元编号，基因编码的顺序就是加工元的加工顺序，M_x和T_x的基因代表机床和刀具的编号，并与加工元一一对应。例如，图1所示染色体各子串包括8个基因，代表1到8个加工元，其中第一个加工的工步是加工元6，对应加工资源为3号机床和1号刀具。

Figure 1. Coding diagram

图1. 编码示意图

采用上述编码方法，解码操作方便快捷。以图1所示染色体为例，通过解码后可得该工艺路线为：

$U_6\left(M_3,T_1\right)-U_{\text{2}}\left(M_3,T_1\right)-U_{\text{8}}\left(M_{\text{2}},T_{\text{2}}\right)-U_{\text{4}}\left(M_{\text{1}},T_1\right)-U_{\text{1}}\left(M_{\text{2}},T_{\text{3}}\right)-U_{\text{5}}\left(M_{\text{3}},T_{\text{3}}\right)-U_3\left(M_{\text{1}},T_2\right)-U_7\left(M_1,T_2\right)$

3.2. 约束检验与修正方法

在工艺规划问题中，各个加工元之间存在优先约束关系，在初始化种群、染色体遗传进化以及模拟退火搜索等进化过程中，都可能生成不可行解。因此本文将约束矩阵引入NSGA-II算法中，对新解进行约束检验并修正不可行解，具体检验与修正步骤如下：

设某染色体个体的加工元编号子串为U_x，r表示某加工元在U_x中的第r位，Pro为零件所有加工元集合，a为Pro中的加工元编号，n为Pro中元素总个数。

步骤1：设a = 1。

步骤2：遍历U_x，寻找pro_a的基因U_x,r。

步骤3：在约束矩阵中搜索加工元pro_a的后续加工元，将其加入U_x,r的后续加工元集合A_r中。

步骤4：令a++，若A_r ≠ Φ，则将U_x中第1位至第r − 1位基因中属于集合A_r的元素，按其在U_x中原本的顺序移动至最后。

步骤5：若a ≥ n，停止检查；否则转到步骤2。

3.3. 选择

本文采用锦标赛选择法和精英选择策略，将父代与子代种群合并为临时种群，从种群中按照每个个体的非支配排序层级和拥挤距离两个属性进行抽取选择，如果非支配层级相同，优先选择拥挤距离大的个体。重复此操作，直至种群规模达到原先种群规模。

3.3.1. 非支配排序

多目标优化问题最终获取一个Pareto最优解集，非支配排序可以引导搜索向Perato最优解的方向趋近。设f₁(x)为低碳目标函数，f₂(x)为高效目标函数，对任意解x₁、x₂，都有f₁(x₁) < f₁(x₂)和f₂(x₁) < f₂(x₂)，则称x₁支配x₂。快速非支配排序就是将种群中不被其他个体支配的个体标记为第1级非支配前端，将这些个体在种群中移除，继续比较剩余的个体，找出新的非支配解作为第2级非支配前端，重复上述操作直至所有个体分级完毕。

3.3.2. 拥挤距离计算

拥挤距离可以更好地了解每个解周围其他解的分布情况，保证解的多样性。拥挤距离是同一支配层级的个体在每个子目标方向上，与其靠近的两个个体的距离差的绝对值之和。个体x的拥挤距离计算方法如式(17)：

$d_x=\left|f_1\left(x+1\right)-f_1\left(x-1\right)\right|+\left|f_2\left(x+1\right)-f_2\left(x-1\right)\right|$ (17)

其中：x + 1和x ‒ 1分别为与个体x相邻的两个个体。

3.4. 交叉

交叉操作如图2所示，首先随机选择两个交叉点，将父代染色体P₁交叉点两端的基因复制给子代染色体O₁相应的位置；然后删除掉父染色体P₂中O₁已有的U_x编号基因及与之对应的M_x和T_x基因，将剩余的基因按照原本顺序依次填入O₁的空余位置中，以此可保证产生的新染色体不违反约束关系。交换P₁、P₂按照相同方法生成子代染色体O₂。

Figure 2. Schematic diagram of cross operation

图2. 交叉操作示意图

3.5. 变异

变异操作如图3所示，在父染色体P₁中随机选择两个变异点，调换三个子串位于变异点的基因。对于M_x和T_x两个子串，随机选择一个变异点，在可选范围内选择机床和刀具序号替换变异点基因。变异后的新个体可能不满足顺序约束，因此要进行约束检验与修正。

Figure 3. Schematic diagram of variation operation

图3. 变异操作示意图

3.6. 改进的NSGA-II算法

基于成绩标量函数的局部搜索

1) 成绩标量函数

ASF函数通过给定参考点 $\bar{z}$ 和权向量ω将多目标函数进行标量化，函数的最小值解是多目标优化问题的Pareto最优解 [16] ，因此本文以此作为评价函数 [17] ，计算方法如式(18)~(19)：

$\{\begin{array}{c}\min F(x)=\underset{s=1,2}{\max }{\omega }_s\left(f_s\left(x\right)-{\bar{z}}_s\right)+\rho {\displaystyle \underset{s=1}{\overset{2}{\sum }}{\omega }_s\left(f_s\left(x\right)-{\bar{z}}_s\right)}\\ \text{s}\text{.t}.x\in \text{D}\end{array}$ (18)

${\omega }_s=\frac{f}{\max f_s\left(x\right)-\min f_s\left(x\right)}$ (19)

其中：D为决策空间； $\bar{z}=\left({\bar{z}}_1,{\bar{z}}_2\right)$ 为各目标函数的理想值； $\omega =\left({\omega }_1,{\omega }_2\right)$ 是两个目标函数进行标量化的权向量； $\max f_s\left(x\right)$ 、 $\min f_s\left(x\right)$ 分别为种群中各目标函数的最大和最小值；增广系数ρ取任意的极小正值。

2) 基于模拟退火操作的局部搜索

传统的NSGA-II算法在后期容易陷入局部最优解，因此本文融入模拟退火算法，利用其Metropolis接受准则来决定是否接受新解，以一定的概率跳出局部极值，提高算法的局部搜索能力。模拟退火算法的求解思路模拟固体徐徐降温时粒子趋于稳定的过程，本文在遗传操作产生新子代种群后，对种群中个体进行退火搜索。为了保证搜索到的新解满足顺序约束，要对其进行约束检验与修正。比较搜索到的新个体与当前个体的ASF函数值，通过接受准则判断是否接受新解替换当前解，接受概率计算方法如式(20)：

$p=\{\begin{array}{c}1F\left(x_{\text{new}}\right)\text{<}F\left(x_{\text{old}}\right)\\ \exp \left[-\frac{F\left(x_{\text{new}}\right)-F\left(x_{\text{old}}\right)}{kB\cdot T_x}\right]F\left(x_{\text{new}}\right)\ge F\left(x_{\text{old}}\right)\end{array}$ (20)

其中：p为接受劣解的概率；F(x)为ASF函数值，x_old为当前解，x_new为搜索到的新解；T_x为当前温度，kB为玻尔兹曼常数。

3) 改进的NSGA-II算法流程

综上所述，本文所采用的改进的NSGA-II算法具体流程如下。

步骤1：输入初始化参数，生成初始化种群，对种群中个体进行约束检验与修正，保证种群个体的合法性。

步骤2：计算种群中个体适应度值。

步骤3：根据适应度值对种群中的个体进行非支配排序和拥挤距离计算。

步骤4：根据锦标赛选择法选择优秀个体，进行交叉和变异操作，为保证解的可行性，对交叉后的个体进行约束检验与修正，生成子代种群。

步骤5：计算子代种群中个体的ASF值，对种群个体进行模拟退火搜索操作并对搜索到的新解进行约束检验与修正。

步骤6：将模拟退火操作后的新种群与父代种群合并，进行适应度评价及选择操作，根据锦标赛选择法与精英选择策略选出优秀个体生成新种群。

步骤7：判断是否达到最大迭代次数，若达到则输出结果；否则返回步骤2。

4. 实例验证

4.1. 实例描述

以图4所示的某型号导向轴支撑座零件为例，验证前文所述低碳高效机械加工工艺优化模型和改进的NSGA-II算法的有效性。该零件主要包含有外圆、端面、孔倒角等10个加工特征，在图4中用F1至F10表示。加工该零件可用的加工机床设备有编号为M1、M2的两种数控车床，M3、M4两种数控铣床，M5、M6两种数控钻床以及M7数控镗床，可选用的刀具信息见表1。

零件的10个特征面共要经过20个加工工步，即其工艺路线由20个加工元组成。零件的各加工特征描述、特征间的约束关系、加工元编号、加工元对应可选资源信息及其相应的加工时间见表2。

根据特征加工客观约束原则，确定加工元之间的约束关系，并根据约束矩阵的建立规则得出加工元之间的约束矩阵R：

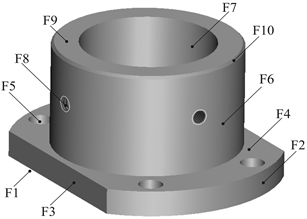
Figure 4. Schematic diagram of machining features

图4. 加工特征示意图

Table 1. Optional tool information

表1. 可选刀具信息

Table 2. Flexible process information table

表2. 柔性工艺信息表

$R=\left[\begin{array}{cccccccccccccccccccc}0& 1& 1& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 1& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 1& 0& 1& 0& 1& 1& 0& 1& 0& 0& 1& 0& 1& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 1& 0& 1& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 1& 0& 0& 1& 1& 0& 1& 0& 0& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1& 0& 0& 0& 1& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 0& 0& 1& 0& 0& 0& 1& 1& 0& 0& 1& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 1& 0& 1& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 0& 0& 0& 1& 0& 0& 1& 0& 1& 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 1& 0& 0& 0& 1& 0& 0& 1& 0& 0& 0& 0& 0& 0& 1& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 1\\ 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0& 0\end{array}\right]$

4.2. 优化结果

算法参数设置为：初始种群规模为50，交叉概率为0.85，变异概率为0.05，最大迭代次数为200，初始温度为100，冷却系数为0.9，结束温度为60。经过仿真实验，得到两个优化目标函数的收敛曲线如图5所示。

Figure 5. Algorithm convergence curve

图5. 算法收敛曲线

为了验证本文改进NSGA-II算法的有效性，与传统的NSGA-II算法进行比较，得到Pareto前沿分布结果，如图6所示。由于实例规模限制，改进NSGA-II算法的优势有一定的局限性。但从直观上看，改进的NSGA-II算法得出的非支配解分布在传统NSGA-II算法的左下角，占据更优位置，获得的最小碳排放和最短完工时间均低于传统NSGA-II算法，表明其搜索空间更大；且传统NSGA-II算法的Pareto解集中存在较多不满足加工顺序约束的不可行解，而改进NSGA-II算法的解集中均为经过约束检验与修正的可行解。由表3可知，改进的NSGA-II算法的Pareto解集平均值及最优值均优于传统NSGA-II算法，平均碳排放和完工时间分别降低了4.3%和3.6%。综上所述，改进的NSGA-II算法优于传统的NSGA-II算法。

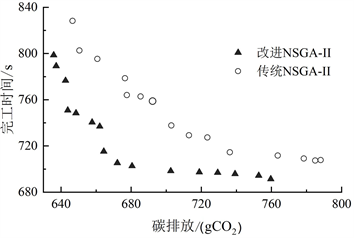
Figure 6. Pareto frontier distribution

图6. Pareto前沿分布

Table 3. Perato unset data statistics

表3. Perato解集数据统计

由Pareto前沿的解的分布图可以看出，随着工艺路线完工时间的增加，碳排放量越来越小，由此说明低碳和高效两个目标无法同时最优。使用改进的NSGA-II算法同时优化两个目标函数，得到最优解集，决策者可根据实际生产需求选择合适的解。如选择解集中两个目标权重接近、优化值都较为满意的解，其染色体解码成为的工艺路线为：

$\begin{array}{l}{U}_1\left(M_1,T_2\right)-U_4\left(M_1,T_1\right)-U_{11}\left(M_1,T_1\right)-U_8\left(M_2,T_2\right)-U_{18}\left(M_2,T_2\right)\\ -U_{13}\left(M_7,T_8\right)-U_2\left(M_2,T_1\right)-U_5\left(M_2,T_2\right)-U_{12}\left(M_2,T_2\right)-U_{14}\left(M_7,T_7\right)\\ -U_{15}\left(M_7,T_7\right)-U_9\left(M_1,T_1\right)-U_{19}\left(M_1,T_2\right)-U_3\left(M_2,T_2\right)-U_{20}\left(M_1,T_1\right)\\ -U_6\left(M_3,T_4\right)-U_7\left(M_3,T_3\right)-U_{10}\left(M_6,T_5\right)-U_{16}\left(M_6,T_6\right)-U_{17}\left(M_5,T_9\right)\end{array}$

该工艺路线碳排放总量为672.18 g CO₂，总完工时间为705 s。该路线权衡考虑了加工元的连续性、加工资源的更换频率和分布情况等，既避免了频繁更换加工资源引起过高的完工时间，又避免了集中选择加工时间短的机床和刀具从而引起附加载荷能耗增大、刀具磨损加剧及切削液用量加大而造成更高的碳排放。

5. 结论与展望

本文通过分析零件机械加工过程的碳排放和完工时间的影响因素，建立了以碳排放最低和完工时间最短为目标的优化模型，使用改进的NSGA-II进行优化求解。以某型号的导向轴支撑座零件为例，验证了所提模型和改进算法的可行性和有效性，结果表明本文的研究对工艺路线规划的低碳高效优化问题有一定的借鉴意义。

1) 采用三段式编码方式对加工路线进行编码，改进了交叉、变异操作，并针对NSGA-II算法后期局部搜索慢的问题，融入模拟退火操作，根据ASF函数值和Metropolis准则更新种群以提高局部搜索能力。

2) 设计了依据加工元约束矩阵的约束检验与修正方法以保证工艺路线的有效性。

3) 工艺路线规划是机械零件加工过程的重要一环，其与加工参数、车间调度对机械加工系统的碳排放及加工时间的影响相互联系。因此，下一步可将工艺路线规划与加工参数、车间调度问题集成优化研究，降低整体机械加工制造系统的碳排放和完工时间。

基金项目

浙江省2023年度“尖兵”“领雁”研发攻关计划(2022C01SA111123)，国家自然科学基金资助项目(51475434)。