1. 引言
雾化喷嘴在燃气轮机、燃烧器、消防、环境、农业等领域有着广泛的应用,可分为机械雾化喷嘴和介质雾化喷嘴两类,机械雾化喷嘴通过压差力和离心力实现液体雾化,结构相对简单,雾化效果相对较差,适用于低粘度液体,介质雾化喷嘴通过高速气体介质实现液体雾化,结构相对复杂,雾化效果好,适用于高粘度液体。
其中机械雾化喷嘴又可分为射流式、离心式和螺旋式,离心式喷嘴根据其内部有无旋流件又可分为有旋流件和无旋流件两种情况,旋流件可以强化喷嘴内部流体的旋转强度进而提升雾化效果,但结构上也会更加复杂。
液体在喷嘴内部的流动及气液之间的相互作用很是复杂,不同类型的喷嘴其雾化机理不同,大体上可分为经典式和瞬发式两类 [1] ,但目前尚未有一种令人完全信服并经得住检验的雾化机理 [2] 。
喷嘴的设计方法相关资料很少且不够详细,常见的有最大流量原理法、当量几何特性法和经验关系图线法等 [3] ,目前有关喷嘴的研究大多针对某款现有的喷嘴进行分析 [4] [5] [6] ,而喷嘴的设计研究很少,本文以简单离心式雾化喷嘴为例(无旋流件),通过上述喷嘴设计方法设计一款简单离心雾化喷嘴,并借助CFD工具探究喷嘴结构参数对雾化性能的影响规律。
2. 喷嘴结构设计与性能表征
2.1. 结构设计
简单离心式雾化喷嘴结构参数主要有进口倾角、进口数量、进口槽宽度、旋流室半径、旋流室倾角、喷孔半径、喷孔长度等,相关几何参数示意图如图1所示。
常见的设计方法有最大流量原理法和当量几何特性法,但相关参数释义不完整,设计过程逻辑也不够清晰,这里对这两种设计方法具体设计过程进行梳理归纳。
最大流量原理法由原苏联学者阿勃拉莫维奇提出,该方法假设流动是对称的,略去了径向速度,未考虑液体粘性,该方法设计过程如下
工况:质量流量qm (kg/s)、压力P (表压Pa)、密度ρ (kg/m3)。

Figure 1. Schematic diagram of nozzle geometric parameters
图1. 喷嘴几何参数示意图
有效截面系数φ
(1)
rc:喷口半径,rp:气核半径。
理论几何特性数A
(2)
S:进口槽总面积,R:旋流半径。
1) 首先根据预期雾化角计算有效截面系数φ
(3)
2) 根据有效截面系数φ计算流量系数μ
(4)
3) 根据有效截面系数φ计算理论几何特性数
(5)
有效截面系数、流量系数和雾化角与理论几何特性关系曲线如图2所示。
4) 根据工况计算喷孔半径rc (mm)
(6)
5) 求单个进口槽长度h和宽度b (mm)
(7)

Figure 2. Theoretical geometric characteristic curve of nozzles
图2. 喷嘴理论几何特性曲线
e:进口槽长宽比,
,e一般大于1。
n:进口槽数量。
R:旋流半径,
,
一般取2~6。
6) 计算旋流室半径Rs (mm)
(8)
至此,喷嘴主要几何尺寸已经确定,相关的理论推导过程可参考相关文献 [7] [8] 。该方法未考虑进口倾角β、旋流室长度
、旋流室倾角θ、旋流半径比
、喷孔长度
等几何参数的影响,此外该方法因忽略径向速度和粘性使所预测的理论几何特性A偏低,使得进口槽面积偏大,进口速度偏小、雾化角偏小,总之该方法预测精度较低,不建议采用。
当量几何特性法在上述基础上考虑了粘性对喷嘴的影响,此外还考虑了旋流室倾角θ、旋流半径比
的影响,设计过程如下:
工况:质量流量qm (kg/s)、压力P (表压Pa)、密度ρ (kg/m3)。
1) 首先根据预期雾化角查表获取当量几何特性参数Ae和流量系数μ
以旋流半径比
,旋流室倾角θ = 30˚为例,根据表中数据对曲线进行拟合得
和
曲线,如图3所示。
经拟合得
2) 根据工况计算喷孔半径rc (mm)
(9)
3) 求单个进口槽长度h和宽度b (mm)
(10)

Figure 3. Nozzle equivalent geometric characteristic curve
图3. 喷嘴当量几何特性曲线
e:进口槽长宽比,
,e一般大于1。
n:进口槽数量。
R:旋流半径,
,
一般取2~6。
4) 计算旋流室半径Rs (mm)
(11)
该方法预测精度相对较高,本文采用该设计方法,设计一款基础喷嘴,采用控制变量的思想,在此基础喷嘴的基础上研究旋流半径R、旋流室倾角θ、喷孔长度
对雾化性能的影响规律。
2.2. 性能表征
1) 压损
(12)
为喷嘴入口压力,
为喷嘴出口压力。
喷嘴在常压下工作时入口压力(表压)即是喷嘴压损,压损越大工作压力越大,能耗也越大。
2) 流量数FN
流量数定义式
(13)
:体积流量(m3/h)。
流量数表征了喷嘴的流通能力,流量数越大,单位压损流过的液体越多。
3) 雾化角α
用不同参数表征雾化角得到的经验公式不同,里兹克(Rizk)和勒菲沃(Lefebvre)提出的雾化角经验公式如下 [9]
(14)
:旋流室直径,
:喷孔直径,
:总进口面积,
:液体压力,
液体动力粘度。
雾化角减小会削弱液膜与周围空气的相互作用,使初始液膜厚度增加,雾化效果变差。
4) 粒径
颗粒粒径的表征常用的方法有直方图、累积分布、罗森–莱姆勒分布和索特尔平均直径(SMD)等,这里采用最常用的索特尔平均直径进行粒径分析。
根据SMD直径的定义,一群个数为N的液滴群,将其看作一群个数为
平均直径为
的液滴群,令假想液滴群的体积与表面积之比与真实液滴群的体积与表面积之比相等,求出的
即为SMD直径
(15)
SMD直径是应用最广的粒径表征方法,尤其是在蒸发燃烧领域,这里采用勒菲沃 [10] (Lefebvre)提出的离心喷嘴的SMD经验公式
(16)
t为喷嘴出口位置液膜厚度,α为雾化角,
液体动力粘度,
液体喷嘴压损,
液体密度。该式描述了雾化喷嘴的结构特性和液体的物性参数对SMD的影响,在不做液滴粒径实验测量的情况下,根据喷嘴内部液体流动特性来预测雾化效果。
3. 数值计算
3.1. 数学模型
结合实际工况,对流动作以下简化:1) 不可压缩;2) 不考虑相间质量传递,相关控制方程如下
连续方程:
动量方程:
多相流方程:
根据周建伟 [11] 的湍流模型仿真对比,相比于SST和RNG,RMS湍流模型能更准确的预测喷口出口位置的气穴,故本文选用RMS湍流模型。
3.2. 几何模型与网格
采用上文当量几何特性法设计一款工质为水、流量0.001、压力0.2、90˚雾化角的离心喷嘴,几何模型如图4所示
采用Fluent Meshing划分网格,最大网格歪斜率小于0.6,对液膜位置做了局部加密,如图5所示对网格无关性进行验证,网格数量为90万时所监测的物理量已无太大变化,故取90万网格数量对应的网格尺寸。
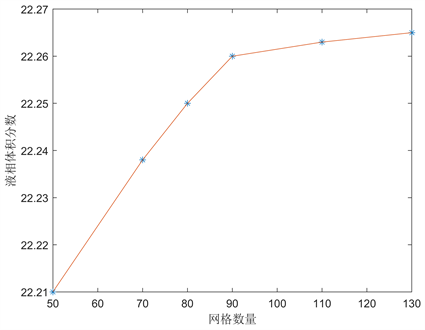
Figure 5. Mesh independence verification
图5. 网格无关性验证
3.3. 工况与边界条件
工况:所有案例采用相同工况,流量0.001 kg/s,压力0.2 MPa,密度998.2 kg/m3,动力粘度0.001003 kg/(m∙s)。
多相流模型:VOF,稳态,Implicit,Compressive。
进口边界:压力进口,0.2 MPa。
出口边界:压力出口,0 MPa。
3.4. 试验设计
Minitab能够生成所有变量组合的曲面图,在其它变量不变的情况下,使用x和y变量拟合响应变量(z),并且能够绘制出平滑曲面,曲面图能够直观的显示响应变量与两个变量的相关程度。本文在基础几何模型的基础上,用Minitab对目标参数进行相应曲面分析,采用Box-Behnken方法设计实验来研究旋流半径、旋流室倾角、喷孔长度对雾化角和流量的影响,试验因素和水平如表1所示,实验设计和结果如表2、表3所示

Table 1. Table of factors and levels
表1. 因素与水平表
4. 结果分析
胡旭财 [8] 采用VOF方法对工况参数和结构参数对离心喷嘴雾化性能的影响进行了分析,并对仿真和试验进行了对标,雾化角的仿真结果和试验结果误差小于5%,误差值较小,表面VOF在离心喷嘴仿真上满足误差要求,本文亦采用VOF对离心喷嘴进行研究,故认为仿真结果满足误差要求。
离心喷嘴主要在压力的驱动下使液体在喷嘴内部获得较大速度并旋转运动,为便于下文分析描述定
义旋流强度
,其中v为切向速度,w为轴向速度,用旋流强度表征离心力的强弱,旋流强度越大离
心力越大,由公式16可知雾化角越大,雾化效果越好。
4.1. 结构参数对雾化角的影响分析
结构参数对雾化角的影响结果如表2所示。

Table 2. Experimental design and atomization angle
表2. 实验设计与雾化角
为i水平结果之和,极差R为
,极差越大表面该因素在取值范围内对结果的影响越大,从表2可以看出喷孔长径比极差最大,故在这三个因素中喷孔长径比对雾化角的影响最大,旋流半径比和旋流室倾角分别次之。此外,大部分模型雾化角皆在90˚左右,说明当量几何特性法设计的喷嘴雾化角与预期较接近,在雾化角的预测上精度较高。
从图6可以看出在喷嘴出口形成了锥形液膜,达到了预期雾化角,但在喷孔内部未形成气核,其余实验也未能在喷孔内部形成气核,说明简单离心喷嘴喷孔内部液体旋转强度不够强,可以通过加装旋流件增强旋流强度来进一步提示雾化效果。

Figure 6. Experiment 1: Gas-liquid interface distribution
图6. 实验1:气液界面分布
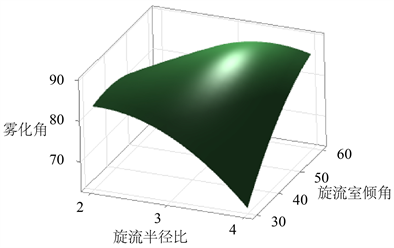
从图7(a)可以看出雾化角随旋流半径比的增大而减小,这是因为流体在旋流室内旋转运动,随着旋流半径比的增大,流动截面积增大,速度降低,旋流强度降低,故雾化角减小,实际中旋流半径比的取值范围一半在2~6之间,故可据此结论在喷嘴设计过程中对旋流半径比进行相应的调整。
 (a)
(a) (b)
(b)
Figure 7. Influence of structural parameters on atomization angle
图7. 结构参数对雾化角的影响

Figure 8. Variation curve of swirl intensity at x = 0.2 mm
图8. x = 0.2 mm处旋流强度沿程变化曲线
从图7(a)可以看出,雾化角随旋流室倾角的增大而增大,图8为试验1和试验3在x = 0.2 mm位置旋流强度沿轴向方向(z方向)的变化曲线,可以看出,旋流强度I沿轴向方向逐渐减小,流体整体上沿轴向方向流动并从喷口流出,因旋流室倾角导致沿轴向方向流动截面积逐渐减小,故轴向速度必然逐渐增大,但从入口槽道获得的旋流强度沿轴向方向因局部阻力和沿程阻力而逐渐消耗,最终导致旋流强度沿轴向方向逐渐减小,故旋流室倾角越大,轴向距离越短,旋流强度衰减越小,出口位置旋流强度越大,雾化角越大。

Figure 9. Speed change curve at x = 0.2 mm
图9. x = 0.2 mm处速度沿程变化曲线
从图7(b)可以看出雾化角随喷孔长径比的增大而减小,图9为试验1在x = 0.2 mm位置切向速度、轴向速度和旋流强度沿轴向方向(z方向)的变化曲线,可以看出切向速度在旋流室内逐渐增大,在喷孔内因切向速度梯度产生粘性损耗进而导致切向速度逐渐减小,轴向速度因流动截面积逐渐减小而逐渐增大,故在喷孔内部旋流强度逐渐减小,因此喷孔长度越长切向速度损耗越大,旋流强度越低,雾化角越小。
4.2. 结构参数对流量的影响分析
结构参数对流量的影响结果如表3。

Table 3. Experimental design and flow
表3. 实验设计与流量
从表3可以看出旋流室倾角的极差最大,故在这三个因素中旋流室倾角对流量的影响最大,旋流半径比和喷孔长径比分别次之。此外可以发现流量皆大于0.001,说明当量几何特性法设计的喷嘴流量偏高,可以对流量系数进行一定修正,但这不影响下文结构参数对流量影响趋势的分析。
 (a)
(a) (b)
(b)
Figure 10. Effect of structural parameters on flow
图10. 结构参数对流量的影响
从图10(a)可以看出流量随旋流半径比的增大而增大,这是因为旋流半径比增大流动截面积随之增大,流动阻力减小,故流量随之增大,所有试验中喷孔直径不变,流动截面积不变,所以流量大意味着出口位置速度大,速度越大液膜与周围空气之间气动作用力越强,液膜表面不稳定波动越剧烈,越有利于液膜的破碎,雾化效果越好。
流量随旋流室倾角的增大而减小,这是因为旋流室倾角形成一个过渡段,沿着流动方向流动截面积逐渐减小,此处流体微团之间剧烈碰撞掺混造成较大能量损失,即存在较大的局部阻力,旋流室倾角越大,流体微团之间碰撞掺混越剧烈,能量损失越大,阻力越大,故流量随之减小,雾化效果随之变差。
从图10(b)可以看出喷孔长径比对流量几乎无影响,这是因为喷孔是直管道,能量损失主要是沿程损失,无局部损失,而沿程损失在总损失中一般占比很小,故对流量几乎无影响。
5. 结论
本文通过数值模拟对离心喷嘴不同设计方法进行了验证,离心喷嘴几何结构参数较多,不同结构参数对不同指标影响不同,本文研究了部分结构参数对喷嘴性能的影响机理,得出以下结论:
1) 旋流半径比增大会使雾化角减小、流量增大;
2) 旋流室倾角增大会使雾化角增大、流量减小;
3) 喷孔长径比增大会使雾化角减小,对流量影响不大;
4) 旋流半径比、旋流室倾角和喷孔长径比三者中喷孔长径比对雾化角影响最大,旋流室倾角对流量影响最大;
5) 按当量几何特性法设计的喷嘴在雾化角上预测校准,在流量上存在较大偏差,该方法可以为喷嘴前期设计提供一定的参考价值;
6) 众多实验均未能在喷孔位置形成气核,说明简单离心喷嘴内部旋流强度不够,可以通过加装旋流件,增强旋流强度来进一步提高雾化效果。
NOTES
*通讯作者。