典型工况下轿运车架有限元仿真及频响特性分析

Finite Element Simulation and Frequency Response Analysis of Carriage Frame under Typical Working Conditions

摘要: 中置轴轿运车在轿车运输领域应用十分广阔，相较于普通轿运车，它有着运输安全性高、装卸车辆便捷等特点。作为中置轴轿运车的核心承载部件，轿运车架的安全性和可靠性是保障轿车安全运输的重要因素。为研究中置轴轿运车车架的动态静力和振动特性，首先，本文通过三维软件Solidworks建立了简化的中置轴轿运车架模型。然后，基于有限元方法，将其导入仿真软件Ansys Workbench中进行三种典型工况下的动态静力分析，对各种工况下轿运车架的应力分布和变形进行了详细讨论。最后，对轿运车架进行了预应力模态分析，分析了轿运车架的固有频率和振型，避免了与发动机频率重合发生共振，为进一步研究中置轴轿运车架的可靠性提供了参考。

Abstract: The car with middle axle is widely used in the field of car transportation. Compared with the ordi-nary car, it has the characteristics of high transportation safety and convenient loading and un-loading of vehicles. As the core bearing part of mid-axle car, the safety and reliability of car frame is an important factor to ensure the safety of car transportation. In order to study the dynamic static and vibration characteristics of mid-axle sedan frame, firstly, a simplified model of mid-axle sedan frame is established by using Solidworks, a three-dimensional software. Then, based on the finite element method, it was imported into the simulation software Ansys Workbench for dynamic and static analysis under three typical working conditions, and the stress distribution and deformation of car frame under various working conditions were discussed in detail. Finally, the prestressed modal analysis is carried out on the carriage frame, and the natural frequency and vibration mode of the carriage frame are analyzed to avoid resonance with engine frequency coincidence, which provides a reference for further research on the reliability of the carriage frame with mid-axle.

1. 引言

随着轿运物流业快速发展，中置轴轿运车在商品车辆运输领域具有非常广阔的应用前景 [1] 。而中置轴轿运车的主要承载部位为车架，针对轿运车车架研究具有十分重要的意义 [2] 。

湖南大学的李伟平 [3] 分别对半挂牵引车车架的四种工况进行了动、静力学分析，并通过多目标优化算法对车架尺寸进行了优化，达到了轻量化的目的。山东科技大学的聂志峰 [4] 对某型号轿运车后举升机构进行了优化，并对新旧机构的五种不同工况进行了有限元建模与分析，提高了该机构的的举升效率。湖南大学的单喜乐 [5] 利用变密度法对重型汽车车架进行了拓扑优化，后对优化后的车架进行了静力分析和多体动力学分析。湖南大学的卢进海 [6] 对某三轴货车车架的扭转、弯曲、弯扭三种工况进行了静力学、动力学分析和模态分析，确定了车架的薄弱位置并校核了强度，明确了其频响特性。

本文以某中置轴轿运车架为研究对象，基于三维建模软件Solidworks建立了轿运车架的简化几何模型，并通过有限元仿真软件Ansys Workbench对其进行了三种典型工况下的动态静力分析和预应力模态分析。分析了轿运车架在匀速行驶、制动和扭转工况下的应力分布与变形情况，也对该轿运车架进行了预应力模态分析，计算得到前六阶固有频率并于发动机的工作频率进行对比，避免了车架与发动机共振，为进一步研究中置轴轿运车架的可靠性提供了参考。

2. 轿运车架几何模型建立及载荷施加

本文以某中置轴轿运车架作为分析对象，首先，根据轿运车架的实物模型在Solidworks中创建三维模型。由于轿运车架结构比较复杂，对有限元分析的可行性和效率有较大影响，因此需要对该模型进行一定的结构简化。具体包括去除了车架蒙皮、删除了小孔和小面以及将一些共用边线的截面简化为一个整体，简化结构后模型如图1所示。在不影响反映轿运车架真实工作状况的条件下提高了有限元分析的效率。

Figure 1. 3D model of the car frame

图1. 轿运车架三维模型

之后导入Ansys Workbench仿真软件，通过划分网格，根据四种不同行驶工况下的轿运车架施加约束和载荷来分析其不同工况下的动态静力特性和振动特性。该轿运车架选用的材料为Q345，其具体材料属性如表1所示。

Table 1. The car frame material properties

表1. 车架的材料属性

本文研究的轿运车架在满载时，可以装载五辆轿车，在正常行驶过程中，车架需要承受的载荷主要是车架自身重量和所承载轿车的重量。本文中，取一辆轿车重量为1600 kg，将8000 kg载荷力简化为均布载荷施加在车架上，方向为竖直向下。

轿运车行驶过程中会有三种典型工况，分别为满载匀速工况、满载制动工况和满载扭转工况。为了研究各个工况下轿运车架的整体应力情况和变形情况，需要根据不同工况施加不同约束来研究轿运车行驶工程中对车架的动态静力影响，如表2所示为轿运车在三种工况下的约束施加情况，其中 $Ux$ 、 $Uy$ 、 $Uz$ 为位移， $Rx$ 、 $Ry$ 、 $Rz$ 为旋转。

Table 2. Constraints under different working conditions

表2. 不同工况下约束情况

3. 轿运车架四种工况下的有限元仿真分析

3.1. 匀速行驶工况

匀速行驶工况模拟的是轿运车在行驶过程中四轮着地，只受重力加速度作用在平坦道路上行驶。

是轿运车最为常见的行驶工况。

如图2所示，车架的最大应力出现在下平台悬挂的连接处，这是由于上方平台承载的三辆轿车重量通过六根立柱传递给了下平台，而下平台的主要支撑部位为悬挂连接处，因此该处应力较为集中，达到77.031 Mpa，远小于材料的屈服极限，满足强度要求。由图3可知，车架在匀速行驶时，最大变形位于车架后端，这是由于车辆在匀速行驶途中，车架后端类似悬臂梁结构，后端承载重量时，相当于悬臂梁前端受力，从而产生了微量的变形，变形值较小，为3.8675 mm。

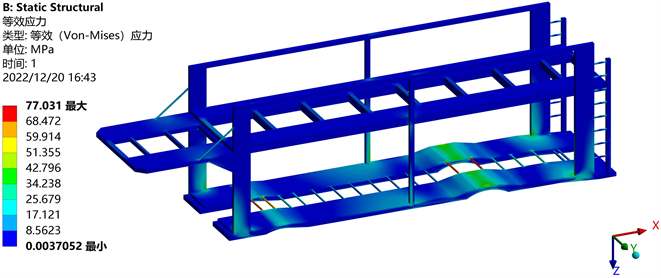
Figure 2. Stress nephogram at constant speed

图2. 匀速行驶工况应力云图

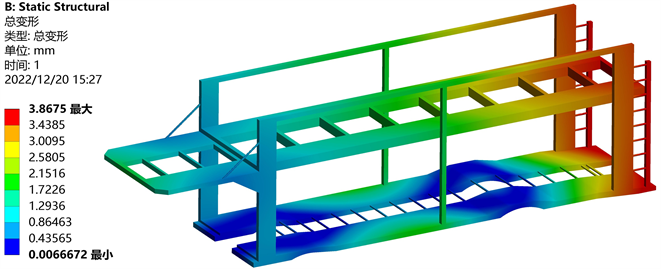
Figure 3. Deformation nephogram at constant speed

图3. 匀速行驶工况应力云图

3.2. 扭转工况

扭转工况是指轿运车在行驶过程中途经凹凸不平路段导致某一车轮悬空，本文中模拟轿运车左前轮悬空的扭转工况。

如图4所示，车架的最大应力出现在下端平台横梁处，主要原因与匀速行驶工况相同，为上平台轿车重量通过立柱传递给了下平台，导致下平台横梁处应力较为集中，其大小为288.8 Mpa，但并未超过材料屈服极限，因此满足强度使用要求。同时，由于路况不平，使车架的一侧抬高，该侧车轮悬空，导致下平台横梁受到较大扭矩，且下平台左右侧的应力情况有明显不同。由图5可知，在扭转工况下，车架的最大变形位于车架上平台左前方，为18.113 mm，同理原因为一侧车轮的抬高，车架发生倾斜，使得其左前方的变形量增大。

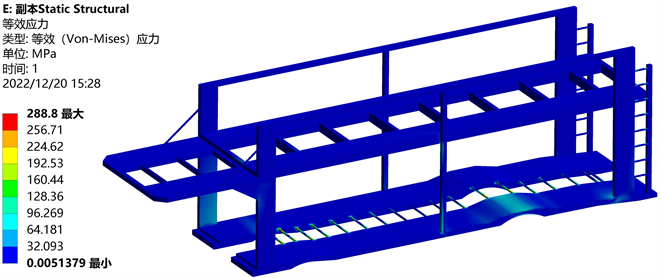
Figure 4. Stress nephogram at torsional condition

图4. 扭转工况应力云图

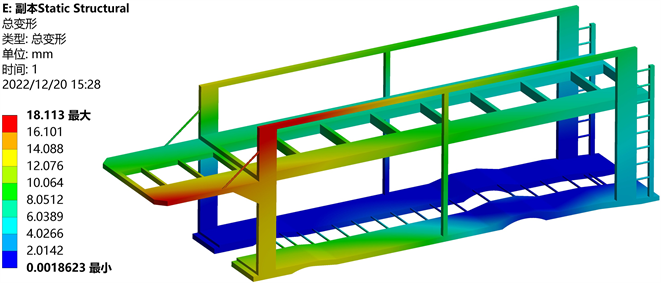
Figure 5. Deformation nephogram at torsional condition

图5. 扭转工况应力云图

3.3. 制动工况

制动工况即轿运车在行驶过程中遭遇紧急情况制动的情形，其载荷约束方式和匀速行驶工况相同，不同的是，车架在制动时除了收到自身的重力影响，还会受到一个与行驶方向相反的制动力，此处给模型施加了一个0.8 g的制动加速度来模拟制动力。

如图6所示，车架的最大应力出现在下平台悬挂的连接处，应力大小为94.426 Mpa，原因是悬挂连接处受到轿车重力和制动力双重作用产生了应力集中，但并未超过材料屈服极限，因此满足强度使用要求。由图7可知，车架在制动工况下，最大变形位于车架上平台前方，为9.6007 mm，原因为施加的制动力产生了较大的惯性载荷使上平台发生了纵向位移。

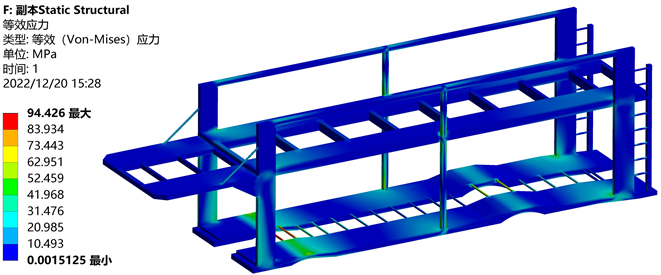
Figure 6. Stress nephogram at brake condition

图6. 制动工况应力云图

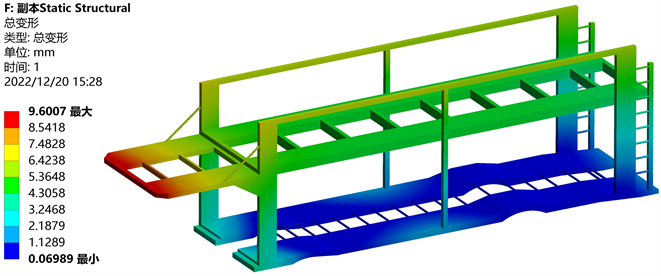
Figure 7. Deformation nephogram at brake condition

图7. 制动工况应力云图

4. 轿运车架的有限元模态分析

4.1. 模态分析概述

对车架进行静力学分析，可以确保再受到恒定载荷作用时，车架能够满足变形、强度等设计要求，然而再轿运车实际的行驶过程中，车架与车辆本身受到的多时不恒定的交变载荷作用，因此对于轿运车架的动力学仿真是十分有必要的。其中模态分析作为最主要的分析方法之一，在分析结构的动力学特性时被广泛应用 [7] 。模态分析有约束模态和自由模态两种。实质上，模态是系统的固有属性，只由其材料自身属性和结构决定，与外部激励等其他因素并无关系。

对于一个系统，其结构的振动微分方程可以表示为：

$\left[M\right]\left\{x{\left(t\right)}^{\prime \text{}\prime }\right\}+\left[C\right]\left\{x{\left(t\right)}^{\prime }\right\}+\left[K\right]\left\{x\left(t\right)\right\}=\left\{F\left(t\right)\right\}$ (1)

式中， $\left[M\right]$ 为系统质量矩阵， $\left[C\right]$ 为系统阻尼矩阵， $\left[K\right]$ 为系统刚度矩阵； $F\left(t\right)$ 为外部激励载荷矩阵； $x\left(t\right)$ 为系统各点的广义向量。

在忽视阻尼影响的条件下，系统的自由振动微分方程可表示为：

$\left[M\right]\left\{x{\left(t\right)}^{\prime \text{}\prime }\right\}+\left[K\right]\left\{x\left(t\right)\right\}=0$ (2)

根据公式求解可得到中置轴轿运车架的各阶固有频率及振型。

4.2. 预应力模态

根据轿运车架在实际行驶过程中大部分时间保持匀速行驶状态，因此本文采用在匀速行驶工况下的预定义模态分析，通过Ansys Workbench选择预应力条件为匀速行驶工况。预应力模态相对于自由模态能更加清晰地描述轿运车架满载下的固有频率和振型。

4.2.1. 模型的建立和网格的划分

在Ansys Workbench中对简化后的车架结构进行网格划分。网格划分的质量与精度对模态分析的结果会产生较大影响，网格划分不规则会导致仿真结果误差较大，同时本文考虑到仿真计算时圆角结构对模态分析的影响，将网格划分四面体网格，网格单元数和节点数分别为155,106及246,352，如下图8所示。

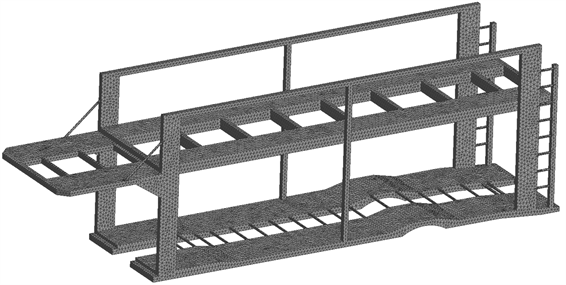
Figure 8. The car frame structure meshing

图8. 轿运车架结构网格划分

4.2.2. 模态分析结果

根据机械振动理论可知，任意系统都具有无限阶的固有频率，但工程实践中影响系统稳定性的只有前几阶固有频率 [8] 。所以，本文在有限元软件中只分析轿运车架的前6阶固有频率和振型，下图9为轿运车架的第1~6阶振型图，由图9可知每一阶的共振部分和振型变形量的大小是不同的；由于预应力模态的匀速行驶工况在车架悬挂处有约束，因此其周边没有出现较大的振幅，这与轿运车架在行驶中情况的相符合。

由上图9可得轿运车架的前6阶固有频率值，如下表3所示。由表3可知，轿运车架在约束条件下从1阶至6阶固有频率大小为3.1235 Hz~17.899 Hz，而轿运车发动机的工作频率约为30~75 Hz，不会发生共振现象，满足设计要求。

(a) (b) (c) (d) (e) (f)

Figure 9. The first 6-order mode of the car frame. (a) The 1 vibration mode; (b) The 2 vibration mode; (c) The 3 vibration mode; (d) The 4 vibration mode; (e) The 5 vibration mode; (f) The 6 vibration mode

图9. 轿运车架前6阶振型图。(a) 1阶振型；(b) 2阶振型；(c) 3阶振型；(d) 4阶振型；(e) 5阶振型；(f) 6阶振型

Table 3. The first 6-order natural frequency and mode characteristics of air filter

表3. 轿运车架前6阶固有频率和振型特征

将上表3中固有频率数值随阶数变化的柱状图绘制于下图10中。

从上图10可知，轿运车架在预应力条件下从1阶至6阶固有频率逐渐增大，其中，第1阶至第2阶固有频率增幅最大，第5阶至第6阶固有频率增幅最小，这与轿运车架的结构及其材料属性密切相关。

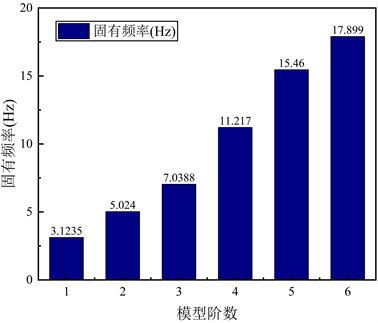
Figure 10. Bar graph of natural frequency with order

图10. 固有频率随阶数变化的柱状图

5. 结论

本文以某中置轴轿运车架为研究对象，通过Solidworks建立了车架的简化几何模型，并通过有限元仿真软件Ansys Workbench对其进行了三种典型工况下的动态静力分析和预应力模态分析，得到了以下结论：

1) 静力学分析结果表明，轿运车架在匀速行驶、制动和扭转工况下的应力值均小于材料屈服强度，符合设计要求。三种工况下最大应力、变形发生的位置均符合轿运车实际行驶状态。

2) 预应力模态分析结果表明，轿运车架前六阶固有频率逐阶增大，最大值为17.899 Hz，小于轿运车发动机最小工作频率30 Hz，不会发生共振现象，证明了该轿运车架具有良好的动态特性。