1. 引言
随着经济的发展和科技进步,现代交通运输业飞速发展,车辆的超限超载对交通安全、运输市场及汽车生产秩序造成了极大伤害 [1] [2] [3] 。主要表现在:1) 使国家税费大量流失,公路的养护费、管理费、通行费都是按车管部门核定的吨位收取,超载必然导致这部分费用的流失。2) 严重损坏了公路基础设施。3) 造成交通事故频繁发生。以上情况促使公路交通部门了解当前公路上行驶车辆的车型组成、轴载谱和超载程度,分析超重车辆对路面损坏的影响程度,以便估算公路交通部门需为此增加的建设投资,并制定相应的管理措施和管理法规,为公路运营部门按车重收费提供有效的技术手段 [4] 。
另外,在厂矿、铁路、港口、生活垃圾分类、垃圾收转运计费等相关车辆设备的作业场景里,也会经常用到车载称重系统。车载动态称重系统与车辆的机械控制部分集成为一体,在车辆作业中实现自动称重。在装载的同时,同步反映装载量,精确装卸,杜绝超载,提高工作效率;收集和监控设备的相关称重数据,可以达到设备运转的透明化监控,方便日常管理。
如何提高动态称重的精度,降低称重系统的成本是一个困扰该行业的难题,国内外一直都在探索寻找更好的动态称重方案。如何设计出速度快、抗干扰能力强、准确度高的新型动态称重,对交通部门有效地实施超限管理、保证行车安全、延长公路的使用寿命、降低公路养护的成本、减小环境污染等方面有着显著的社会效益和经济效益。
2. 总体方案
影响车载动态称重系统称重精度和稳定性的因素很多 [5] ,可分为确定性因素和不确定性因素两大类。其中,确定性因素主要有:
1) 不同类型的车载设备,几何结构受力/动力学姿态模型复杂多变;
2) 上料过程速度快,可采样时间短;
3) 整个上料过程一般为变速曲线运动,运动轨迹复杂。
不确定性因素主要有:
1) 机械结构件本身存在加工精度误差;
2) 液压系统容易受外界温度/液压油品类/阀体差异影响;
3) 车辆底盘的轮胎以及道路起伏程度和坡度影响;
4) 工作时车载设备本身受发动机等抖动影响;
5) 环境温度等会影响设备本身运动特性,车载传感器的采样精度。
以上因素都会不可避免地影响到车载动态称重系统的精度和稳定性 [6] 。本文提出一种软件算法(该方法在原有称重系统上不增加任何硬件成本,只通过改进软件控制算法并实车验证),可以较大程度地筛分掉干扰数据,提取到合适的采样数据,并拟合出合理的数据曲线,从而提升整个车载动态称重系统的精度。
该系统方案硬件部分主要有控制器、显示器、压/应力传感器、位置传感器、电缆线束等。软件算法主要涉及两项关键技术:一是数据的采集与有效处理;二是动态称重特性曲线高度拟合。
3. 数据采集与处理模块
典型的车载动态称重系统,力传感器的信号采集图如下图1。以黑色中位线为界,蓝色线显示的是连续两次完整的上料过程(装料–上升–卸料–回位)的实时曲线图。
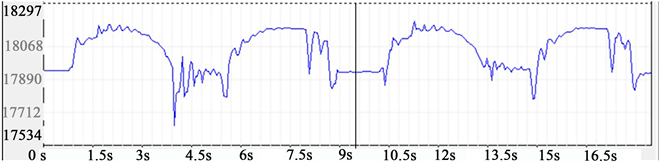
Figure 1. Raw sampling curve of the force sensor
图1. 力传感器原始采样曲线图
1) 常见的动态采样数据处理技术有 [7] :积分法、平均值法、参数估计的系统辨识法、经验模态分解法以及神经网络算法。其中,平均值法是动态称重数据处理常用的方法,这种方法取传感器输出信号相对稳定部分分析,通过计算信号相对稳定部分的有效均值,从而来估算装载装置的实时重量。但是由于动态车辆称重系统的复杂性,采集到的传感器信号中往往包含各种各样的干扰,因此结果一直未能令人满意。
2) 本文采用一种改进后的均值滤波法 [8] :非对称数据自动筛分离群值算法(Automatically Sieving Separation Group Value of Asymmetric Data,简称ASSAD方法)来进行动态称重系统采集数据的处理。实验结果表明,该算法能较好地去除系统干扰噪声影响。

Figure 2. Schematic diagram of sampling interval
图2. 采样区间示意图
3) 上述图2中的绿色矩形框中显示的是在设备装料举升过程中,力传感器采集的实时信号变化曲线,此曲线段近似为梯形。由于装载机构在举升过程中振动大,从而导致曲线抖动明显。另外,在举升到位和下放到位的过程中,整个装载机构容易受到系统冲击。使用中应该去除冲击和抖动影响,保留合适区间的采样值作为计算依据。
4) 非对称数据自动筛分离群值(ASSAD)算法的具体流程:
a) 对区间采样值进行排序,去掉一半小的采样数据,保留一半大的采样数据;
b) 求出剩下的一半大的采样数据的均值回归曲线;
c) 依次计算这部分较大采样数据,与回归曲线之间的距离;
d) 依据各个点与回归曲线的距离值,进行自动排序,去掉距离较远的离群值;
e) 根据K近邻(K_NN)算法,筛选出离均值回归曲线较近的那部分数据均值,作为有效值。
5) 采样数据处理流程图如下图3
6) 采样结果分析
本文截取了一段典型的动态称重过程中的采样数据,如下图4所示,共计25组原始数据。
经过初次排序筛分处理后的剩余数据如下图5所示。
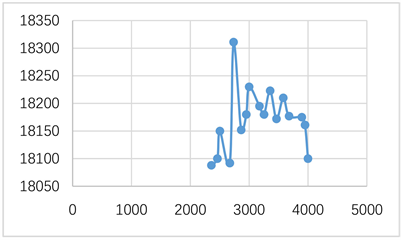
Figure 5. Data after initial screening
图5. 初次筛分后的数据
经过算法自动筛分离群值后,最后保留的有效数据如下图6所示。从图中可以看出,该算法可以较好地去除采样过程中的噪声干扰。
4. 称重特性曲线拟合模块
车载动态称重系统,一般先选取几个特定的重量进行标定。标定完成后,通过算法拟合出一条全量程的称重特性曲线。得到了特性曲线,就可以根据采样变化,实时计算出当前的装载重量。工程上一般常用最小二乘法来解决曲线拟合的问题。最小二乘法的基本思想是:给定一组数据(一般是二维数组,包含X和Y坐标),根据误差平方和最小化原则,找出这些数据的最近匹配函数。如果采用多次曲线函数来拟合所有数据,算法难度和复杂度很大。本文介绍采用递推最小二乘法(简称LRS)分段直线拟合来代替曲线拟合,从而建立车载称重曲线模型 [9] [10] [11] [12] 。
1) 递推最小二乘法分段原理
先取二维数组的前两个点A (X1, Y1)、B (X2, Y2),利用最小二乘法求出拟合直线的数学模型Y = K*X + B。再取第三个点C (X3, Y3),计算出点B和点C确定的直线方程的斜率K。斜率K与K的几何关系如下图7所示。如果tanθ小于给定的阈值,则把C点与前面的点放在一起,再用最小二乘法重新计算拟合直线方程。依次类推,直到发现有大于给定的阈值,这样就完成了第一段拟合直线方程。然后从大于的这个点开始分段,与后续的点重复前面的步骤,直到所有的点都完成拟合。
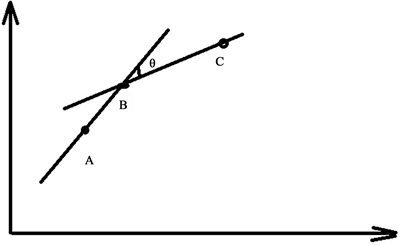
Figure 7. Schematic diagram of the principle of the recursive least squares method
图7. 递推最小二乘法原理示意图
2) 算法逻辑流程
a) 输入阈值ɣ = 设定值,a = 1,j = 2,同时记录这N个点的坐标(Xn, Yn);
b) 对第a个点到第j个点,这几个点用最小二乘法计算出拟合直线方程:Y = K*X + B;
c)分别计算出K,K = (Yj + 1 − Yj)/(Xj + 1 − Xj);
d) 如果j + 1 > N,则停止计算,输出Y = K*X + B;
e) 如果tanθ ≤ ɣ,则j = j + 1,跳转到步骤2;
f) 如果tanθ > ɣ,则输出Y = K*X + B,跳转到步骤7;
g) 对于j、j + 1这两个点用最小二乘法给出拟合直线方程Y = K*X + B,令a = j,j = j + 1,跳转到步骤3,直至所有的点完成拟合。
3) 结果分析
本文截取车载动态称重测试中的一次实验数据,做称重特性曲线拟合测试,一共进行了12组数据标定,见下表。
12组数据采用多次曲线拟合的结果如下图8所示。
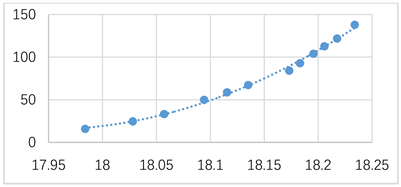
Figure 8. Multiple curve fitting diagram
图8. 多次曲线拟合图
多次拟合曲线方程:Y = 1437.3*X2 – 51587*X + 462895,拟合准确度为R2 = 0.9961。
如图9,分段拟合直线一方程:Y = 350.69*X − 6295.1,拟合准确度为R2 = 0.9761。
如图10,分段拟合直线二方程:Y = 875.21*X − 15821,拟合准确度为R2 = 0.9991。
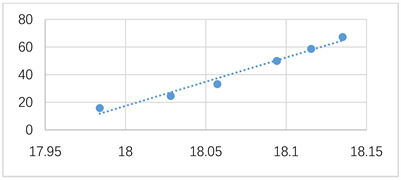
Figure 9. Segmented fitting straight line 1
图9. 分段拟合直线一
从上述三个拟合图形中可以看出,采用多项式曲线拟合后的系统精度为99.61%,采用分段直线拟合后的系统整体精度为98.76%。采用分段直线拟合后的系统精度虽略有下降,但是实时性更好,同时大大降低了算法的复杂度。
5. 结论
本文提供了一种车载动态称重系统的软件控制方法,通过对采样数据进行合理的筛分和优化,保留处理后的有效数据作为模型计算的原始依据。同时,通过采用递推最小二乘法原理,拟合出设备的动态称重特性曲线,从而计算出车载设备的实时装载量,作为设备作业过程中重要的工况数据保存。
本文涉及的车载动态称重系统软件控制方法,不影响原设备的硬件结构,实施成本低,适配性强,兼容性好。此方法已经在环卫设备的后装式垃圾压缩车和侧装式垃圾压缩车、以及地下矿用铲运机上进行了充分样机验证,整体称重精度能控制在90%~95%左右,可以进行批量推广。