1. 引言
随着社会经济的发展与人民生活水平的提高,自动扶梯作为一种常用的人员运输工具,已被广泛应用于商场、机场、地铁、火车站等人流密集场所。扶梯桁架,作为其主要支撑结构 [1],不仅需要在强度上保证扶梯的正常运行,同时需要考虑在各种意外情况发生时,仍能保持乘客的安全,包括在地震发生时,不会对乘客造成附加伤害。
目前,国内外一些学者对自动扶梯桁架的力学性能分析和设计进行了相关研究。徐伟通 [2] 在常规工况下对自动扶梯关键零部件的力学特性展开了仿真研究,给出了最大变形出现的位置。高原 [3] 分析了船用自动扶梯桁架在各种晃动工况下的静强度问题。周游 [4] 基于ANSYS分析了型材偏差对桁架挠度的影响。方晓旻 [5] 提出了扶梯桁架轻量化的方法。陈杨 [6] 基于APDL和VB的二次开发技术,开发了一套扶梯桁架结构有限元自动建模与分析系统。Jiang Jie [7] 基于有限元法和Visual C + +的二次开发及数据接口技术,开发了扶梯桁架参数化有限元分析平台。Xiaowei Yin [8] 建立了扶梯桁架参数化模型,对扶梯桁架系统进行了可靠性分析。以上扶梯桁架的研究限于常规工况下静强度分析和快速建模技术,针对地震工况下扶梯桁架力学性能分析未有涉及。
本研究基于地震情况下自动扶梯的设计要求(中国和日本国家标准) [9] [10],模拟特大地震时建筑物层间变形对扶梯桁架挤压,进行了桁架压缩实验,并通过建立扶梯桁架精细化有限元模型,进行非线性后屈曲分析,得到扶梯桁架压缩过程的力学特性。对比仿真与实验结果,验证建模和仿真方法的有效性。
2. 后屈曲分析基本理论
2.1. 有限元理论
有限元方法的基本思想时将结构离散化,用有限个简单的单元来表示复杂的对象,单元之间通过有限个节点相互连接,结构离散化以后,在运动状态中各节点的动力平衡方程如下:
(1)
式中:
、
、
分别为惯性力、阻尼力和动力载荷,均为向量;
为弹性力。
弹性力向量可用结点位移
和刚度矩阵
表示如下:
(2)
根据达朗贝尔原理,可利用质量矩阵
和节点加速度
表示惯性力如下:
(3)
假设结构具有黏滞阻尼,可用阻尼矩阵
和节点速度
表示阻尼力如下:
(4)
将式(2)、(3)、(4)带入式(1),得到动力学方程如下:
(5)
2.2. 牛顿-拉普森迭代法
由于地震下建筑物层间变形引起扶梯桁架的几何形状变化,造成结构刚度矩阵跟随几何形状变化,导致几何非线性的问题。此时,刚度矩阵不再是常数,而是与位移相关的函数。因此求解非线性问题根本就是求解如下非线性方程:
(6)
由于近似线性方程组建立的方法可以各不相同,因而形成了非线性方程组的各种解法。对于工程问题一般使用迭代法进行求解,常用的迭代方法有:直接迭代法(简称N-R法)、修正牛顿法、拟牛顿法和弧长法。
牛顿法的基本思想如下:
考虑单变量
的线性方程:
(7)
在
处泰勒展开,只保留线性项,得到:
(8)
设
,上式的解为:
(9)
重复上述过程,得到
的第
次近似解为:
(10)
回到非线性方程组式(6)。设
是上式的第
次近似解,在
处将
展开,并且只保留线性项,由此重复得到第
次近似解如下:
(11)
式中:
为切线刚度矩阵。
2.3. 求解方法
上述问题本质上就是求解式(5),要求解式(5),必须解决以下两个问题:一是结构质量矩阵
、阻尼矩阵
和刚度矩阵
;二是必须找到求解式(5)这种大型二阶微分方程组的有效方法。
在动力计算中可采用两种质量矩阵,即协调质量矩阵和集中质量矩阵。二者计算精度相近,但是集中质量矩阵将结构的质量平均分配到单元的各个节点上,即只有对角线上的元素为非零值,对于大规模计算,采用集中质量矩阵可大大减少计算量。因此,本研究采用的是集中质量矩阵。考虑到实验中油压机压缩为缓慢压缩,压缩中能量的耗散可以忽略。因此本研究忽略了阻尼的影响。由于压缩中存在非线性效应,刚度矩阵
为位移的函数,因此刚度矩阵与非线性算法有关。
ANSYS中针对式(5)提供两种求解方法,模态法和积分法。其中积分法又可分为完全积分法和缩减积分法。根据迭代求解中间隔多久修正一次切线刚度矩阵,完全积分法又可分为完全Newton-Raphson方法、修正Newton-Raphson方法和初始刚度法。模态法、缩减积分法以及完全积分法中的初始刚度法、修正Newton-Raphson方法均不允许存在大变形等非线性特性,因此本研究采用的是完全Newton-Raphson方法。
通过完全Newton-Raphson求解法将一系列非线性问题转化为线性问题后,使用稀疏矩阵法进行求解。
3. 压缩试验
在地震中由于建筑物的层间变形而导致上下层建筑物的梁等支撑物间隔距离出现变化,易发生扶梯桁架支撑角钢不能获得建筑物的支撑,即扶梯桁架支撑角钢从建筑物中获得的水平支反力为零或者负值,则自动扶梯主体会发生坠落的情况。
为了模拟地震时建筑物的层间变形对自动扶梯桁架的压缩,采用油压机对某型号自动扶梯进行压缩实验。实验用自动扶梯的提升高度3000 mm,水平跨距9476 mm,倾斜角度30˚,如图1所示。
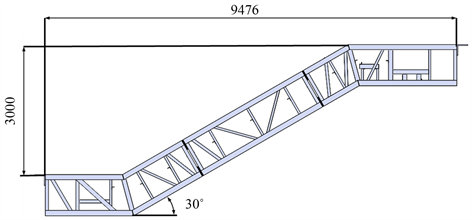
Figure 1. Basic parameters diagram of escalator
图1. 自动扶梯基本参数示意图
3.1. 扶梯桁架结构
自动扶梯桁架主要由上下弦材、竖材、斜材、中间横梁等组成,通过焊接的方式进行连接。其中上、下弦材采用的不等边角钢,竖材及部分斜材采用等边角钢,中间横梁采用等边角钢及槽钢。扶梯桁架截面型材如表1所示。

Table 1. Steel model of escalator truss
表1. 扶梯桁架截面型材
3.2. 实验方法
根据GB/Z 28597-2012中的规定:为防止自动扶梯坠落,需要将自动扶梯一端的支撑角钢固定在建筑物的梁等支撑物上,另一端与支撑物之间需留有足够的搭接量;安装自动扶梯的建筑物在受到地震力影响时其层间变形角应在1/100以下,经过换算强制压缩位移为195 mm。
对实验中底部支撑结构与扶梯桁架支撑角钢固定方法如图2所示,上部支撑角钢通过螺栓固定在上部架台上,下部支撑角钢搭接在底部架台上。实验过程如表2所示,逐步的压缩和卸载,直至压缩量为195 mm。
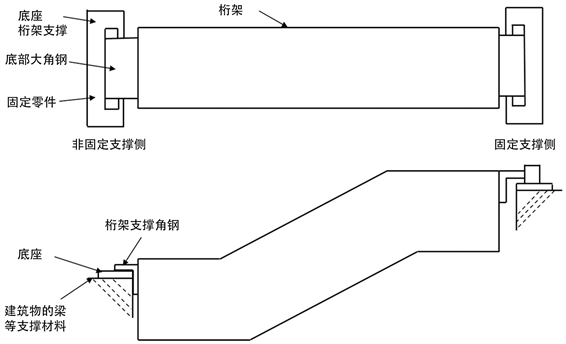
Figure 2. Experimental support diagram of escalator truss
图2. 扶梯桁架实验支撑示意图
乘客载荷及其他机器载荷(梯级、驱动系统等),根据其质量通过悬吊重块的方式施加在扶梯桁架横梁上,如图3所示。
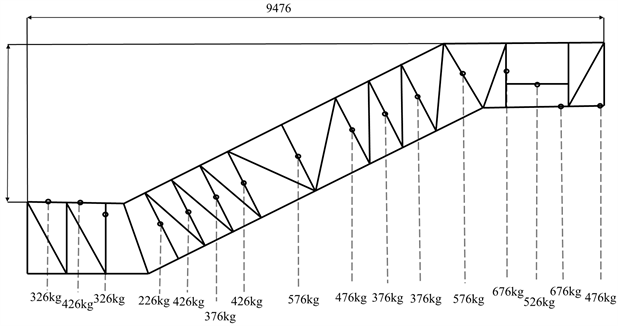
Figure 3. Diagram of experimental lifting block
图3. 实验吊重块示意图
3.3. 实验结果
为了获得扶梯桁架支撑角钢水平支反力随压缩量的变化关系,实验测量扶梯桁架底部被压缩大角钢的位移值及上部大角钢与支撑物间的水平支反力,得到了桁架支撑角钢水平方向水平支反力随压缩量大小变化曲线。
假设乘客乘坐扶梯上行,乘客右手侧为实验所指右侧。扶梯桁架变形形态如图4(a)所示,变形位置在下转折处,变形方向朝向右侧。桁架支撑角钢水平方向支反力随压缩量大小变化曲线如图4(b)所示。
4. 精细化有限元模型
为了节约实验成本,通过建立扶梯桁架精细有限元模型,对以上实验过程进行仿真分析,从而精准模拟地震下建筑物层间变形对扶梯桁架的挤压过程,对扶梯桁架在此状况下的力学特性进行预测。
采用shell181单元模拟扶梯桁架各型材,shell181单元为四节点壳单元,支持非线性、应力刚化、大应变和大变形分析,适合分析板壳结构等多种结构 [11]。
 (a) 实验后桁架变形形态
(a) 实验后桁架变形形态  (b) 实支撑角钢水平支反力随压缩量大小变化曲线
(b) 实支撑角钢水平支反力随压缩量大小变化曲线
Figure 4. Truss deformation diagram after experiment and reaction-compression curve
图4. 实验后桁架变形形态及支反力–压缩量曲线
仿真边界条件设置如下:上部支撑大角钢全约束(6个自由度),底部支撑大角钢释放x方向自由度,约束其他5个方向自由度,悬吊重块的质量以质量点的方式加在仿真模型对应位置。
4.1. 材料
扶梯桁架型材材料特性如表3所示。
以上弦材为例,说明其材料特性的定义。
常用的弹塑性材料插值模型有双线性以及多线性材料模型。为了更加真实的逼近塑性段的材料特性,采用多线性材料模型(6线性段)拟合材料应力–应变曲线。如图5所示。其他部件型材均采用的同样的材料插值模型。
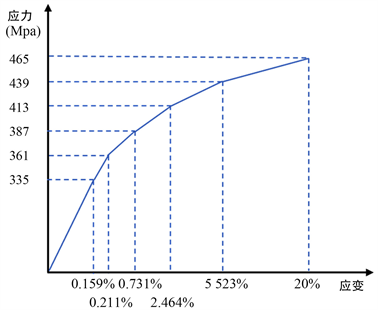
Figure 5. Material characteristic curve of upper chord
图5. 上弦材材料特性曲线
4.2. 焊缝
实验中扶梯桁架下转折处变形严重,为了精确模拟扶梯桁架压缩过程的后屈曲力学特性,同时考虑到计算成本,在图6所示的位置添加焊缝(所标注线条为焊缝),焊缝根据实际几何尺寸采用6 mm × 9 mm的shell181单元。
4.3. 结构初始缺陷
由于扶梯桁架装配是分段进行,难免存在尺寸误差,从而导致扶梯桁架存在的左右不对称的问题,称之为结构初始缺陷。显然,此初始缺陷会对扶梯桁架压缩后力学特性产生影响。因此,需要建立精细化有限元模型,分别考虑初始缺陷存在位置(左侧或者右侧)、初始缺陷大小(4 mm~10 mm)对扶梯桁架后屈曲仿真结果的影响。
以图7说明初始缺陷的位置及其大小,图7为初始缺陷在右侧,大小为6 mm。
分别建立以下有限元模型:1) 无初始缺陷模型;2) 初始缺陷分别在左侧、右侧,大小分别为4、5、6、7、8、9、10 mm的模型,并进行相应的分析,并与图4对比。结果如下:
a) 无初始缺陷的模型,仿真分析的变形位置与实验相同,但变形方向与实验相反;
b) 初始缺陷在左侧的模型,各初始缺陷数值大小不同的变形位置与实验结果相同,同样也存在变形方向与实验相反;
c) 初始缺陷在右侧的模型,各初始缺陷数值大小不同的变形位置及变形方向均与实验相同,其桁架支撑角钢水平支反力随压缩量大小的变化曲线如图8所示。
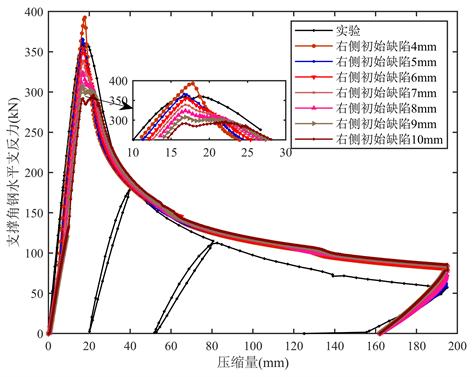
Figure 8. Curves of the reaction force of the horizontal support angle steel with the compression amount
图8. 支撑角钢水平支反力随压缩量大小变化曲线
4.4. 仿真与实验对比
4.3节中初始缺陷在右侧,数值为6 mm时的仿真分析结果与实验结果最为接近,因此进一步对此结果与实验结果进行详细的分析和对比。
压缩解除后仿真分析桁架变形形态如图9(a)所示,桁架支撑角钢水平支反力随压缩量大小变化曲线如图9(b)所示,仿真分析与实验数据对比见表4所示。
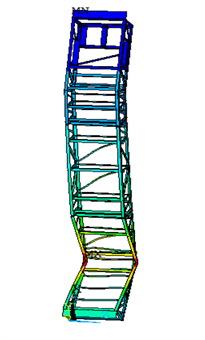 (a) 仿真扶梯桁架压缩形态
(a) 仿真扶梯桁架压缩形态 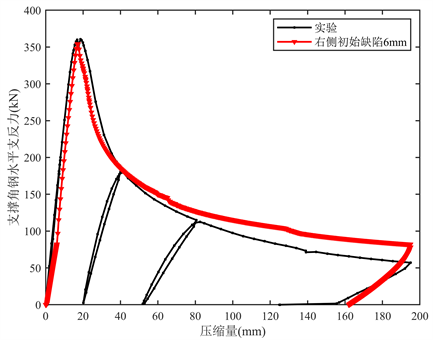 (b) 支撑角钢支反力随压缩量大小变化曲线
(b) 支撑角钢支反力随压缩量大小变化曲线
Figure 9. Simulation and experimental comparison
图9. 仿真与实验对比

Table 4. Comparison of simulation and experimental data
表4. 仿真与实验数据对比
仿真分析变形方向与实验一致,最大支反力大小及相应压缩位移量均吻合较好,强制位移撤销后,桁架也产生一定的回弹,并且回弹量与实验相比误差在4.18%。
5. 结论
为了分析地震导致的建筑物层间变形是否会使自动扶梯“坠落”,基于自动扶梯抗震设计标准,进行了扶梯桁架实物压缩实验,并考虑材料多线性模型、桁架焊缝和桁架几何尺寸误差的影响建立了扶梯桁架精细化有限元模型,进行了扶梯桁架后屈曲分析,获得了桁架压缩后的形态和扶梯桁架支撑角钢的水平支反力随压缩量大小变化的曲线。仿真分析的扶梯桁架后屈曲形态和位置均与实验结果一致,最大水平支反力和桁架强制压缩量撤销后的回弹量误差均小于5%,表明此精细化有限元模型和分析方法可适用于扶梯桁架抗震设计仿真分析。
基金项目
国家自然科学基金资助项目(52005377)。