三相六开关PFC整流器的无差拍控制仿真研究

Simulation Study on Deadbeat Control of Three-Phase Six-Switch PFC Rectifier

摘要: 针对三相六开关PFC (功率因数校正)整流器工作模态多、控制复杂的问题，本文在建立了基于三相静止坐标系和两相旋转坐标系的变换器等效数学模型的基础上，对三相六开关电路提出了基于无差拍控制的电流内环控制和PI控制的电压外环控制的策略，并进行了控制器设计。采用MATLAB/SIMULINK进行了原理仿真，结果表明在稳态运行及负载突变的情况下，输入电流可以跟随输入电压，实现功率因数校正，验证了上述方案的可行性。

Abstract: In view of the problems of multiple working modes and complex control of three-phase six-switch PFC (power factor correction) rectifier, based on the establishment of the equivalent mathematical model of the converter based on three-phase static coordinate system and two-phase rotating coordinate system, this paper proposes the strategy of current inner loop control based on deadbeat control and voltage outer loop control based on PI control for three-phase six-switch circuit, and designs the controller. The principle simulation using MATLAB/SIMULINK shows that the input current can follow the input voltage to realize power factor correction under the condition of steady state operation and sudden load change, which verifies the feasibility of the above scheme.

1. 引言

随着各类电力电子设备的广泛应用，电网中谐波污染增加，无功功率损耗增加，导致电能质量及电能转换效率下降。作为抑制谐波对电网污染的有效手段，功率因数校正(PFC)装置得到广泛应用。与加入滤波器的电网补偿手段相比，PFC控制输入电流跟随输入电压相位，从根本上进行谐波抑制 [1]。针对大功率应用场合的三相功率因数校正装置是目前的研究热点，其中三相六开关拓扑结构作为实现功率因数校正最简单的拓扑结构，半导体器件数量少，可以工作在连续导通模式下。三相六开关的典型控制方法多采用SVPWM控制、平均电流控制、单周期控制。其中SVPWM控制算法复杂，设计步骤繁琐，单周期控制需要快速积分器，稳态精度低 [2]。本文选用三相六开关整流器作为主要研究对象，以所建立的三相静止坐标系数学模型为基础，对三相六开关电路提出了基于无差拍控制的电流内环控制和PI控制的电压外环控制的策略，利用MATLAB/SIMULINK进行了原理仿真，为实物电路控制器设计奠定基础。

2. 变换器的数学模型

如图1所示为三相六开关主电路，基于主电路结构，考虑到部分器件非理想、存在一定阻抗，根据基尔霍夫电压定律(KVL)可以得到式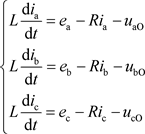(1)：

(1)

式(1)中，e_k (k = a, b, c)为输入电压；i_k (k = a, b, c)为输入电流；U_kO (k = a, b, c)为输出侧k点与O点电压，R为线路阻抗即R_s与R₁之和。

根据基尔霍夫电流定律(KCL)和系统的对称性可得三相六开关PFC变换器在abc三相静止坐标系下的数学模型如式(2)：

$\{\begin{array}{l}L\frac{\text{d}{i}_{\text{a}}}{\text{d}t}=e_{\text{a}}-R{i}_{\text{a}}-\left(\frac{2S_{\text{a}}-S_{\text{b}}-S_{\text{c}}}{3}\right)U_{\text{dc}}\\ L\frac{\text{d}{i}_{\text{b}}}{\text{d}t}=e_{\text{b}}-R{i}_{\text{b}}-\left(\frac{-S_{\text{a}}+2S_{\text{b}}-S_{\text{c}}}{3}\right)U_{\text{dc}}\\ L\frac{\text{d}{i}_{\text{c}}}{\text{d}t}=e_{\text{c}}-R{i}_{\text{c}}-\left(\frac{-S_{\text{a}}-S_{\text{b}}+2S_{\text{c}}}{3}\right)U_{\text{dc}}\\ C\frac{\text{d}{U}_{\text{dc}}}{\text{d}t}=i_{\text{a}}{S}_{\text{a}}+i_{\text{b}}{S}_{\text{b}}+i_{\text{c}}{S}_{\text{c}}-\frac{U_{\text{dc}}}{R_{\text{o}}}\end{array}$ (2)

Figure 1. Three-phase six-switch PFC converter

图1. 三相六开关PFC变换器

abc三相静止坐标系下的数学模型物理意义清晰直观，但由于三相输入电流的耦合性，可通过坐标转换，将该模型转换到与输入电压频率同步的两项旋转d-q坐标系下，降低复杂度同时实现解耦，得出的数学模型可以简化控制系统的设计。可以求得三相六开关PFC变换器在两相旋转坐标系下的数学模型如式(3) [3] [4] ：

$\{\begin{array}{l}L\frac{\text{d}{i}_{\text{d}}}{\text{d}t}=e_{\text{d}}-R{i}_{\text{d}}+\omega L{i}_{\text{q}}-S_{\text{d}}{U}_{\text{dc}}\\ L\frac{\text{d}{i}_{\text{q}}}{\text{d}t}=e_{\text{q}}-R{i}_q-\omega L{i}_{\text{d}}-S_{\text{q}}{U}_{\text{dc}}\\ C\frac{\text{d}{U}_{\text{dc}}}{\text{d}t}=i_{\text{d}}{S}_{\text{d}}+i_{\text{q}}{S}_{\text{q}}-\frac{U_{\text{dc}}}{R_{\text{o}}}\end{array}$ (3)

3. 无差拍控制策略

3.1. 无差拍控制的引入

本文提出的无差拍控制实质为通过在每个控制周期内根据当前输出反馈信号以及对下一周期电流信号的预测进行精确计算，控制下一个周期的占空比，从而实现电流跟踪电压相位的控制策略。无差拍控制的复杂度并不高，同时具有很好的响应速度，跟踪性能优越，控制精度高 [5] [6] [7] [8]。如下图2所示为无差拍控制原理，通过当前周期的状态对下一个周期进行控制。图2中r(k)为k时刻指令信号，u(k)为k时刻控制量，x(k)为k时刻状态变量，y(k)为k时刻输出量，Z⁻¹为超前环节，A、B、C为状态矩阵。

Figure 2. Deadbeat control principle

图2. 无差拍控制原理

3.2. 流内环控制器设计

根据图2的原理框图，可列系统的状态方程：

$\{\begin{array}{l}x\left(k+1\right)=Ax\left(k\right)+Bu\left(k\right)\\ y\left(k\right)=Cx\left(k\right)\end{array}$ (4)

由式(4)有 $y\left(k+1\right)$ 为：

$y\left(k+1\right)=CAx\left(k\right)+CBu\left(k\right)$ (5)

若 $r\left(k+1\right)=y\left(k+1\right)$ ，则有：

$r\left(k+1\right)=CAx\left(k\right)+CBu\left(k\right)$ (6)

由上式(6)可知，当控制量 $u\left(k\right)$ 选取得当时，可以实现系统k + 1时刻的输出量与指令值相等，实现系统的无差拍控制。

三相六开关PFC变换器在两相旋转dq坐标系下的数学模型：

$\{\begin{array}{l}L\frac{\text{d}{i}_{\text{d}}}{\text{d}t}=e_{\text{d}}+\omega L{i}_{\text{q}}-R{i}_{\text{d}}-u_{\text{d}}\\ L\frac{\text{d}{i}_{\text{q}}}{\text{d}t}=e_{\text{q}}-\omega L{i}_{\text{d}}-R{i}_{\text{q}}-u_{\text{q}}\end{array}$ (7)

式(7)的矩阵形式为：

$\left[\begin{array}{l}\frac{\text{d}{i}_{\text{d}}}{\text{d}t}\\ \frac{\text{d}{i}_{\text{q}}}{\text{d}t}\end{array}\right]=\left[\begin{array}{cc}-\frac{R}{L}& \omega \\ \omega & -\frac{R}{L}\end{array}\right]\left[\begin{array}{l}{i}_{\text{d}}\\ i_{\text{q}}\end{array}\right]+\left[\begin{array}{cc}\frac{1}{L}& 0\\ 0& \frac{1}{L}\end{array}\right]\left[\begin{array}{l}{e}_{\text{d}}-u_{\text{d}}\\ e_{\text{q}}-u_{\text{q}}\end{array}\right]$ (8)

对上式进行离散化处理(忽略电阻R)，T_s为采样周期，则：

$\left[\begin{array}{l}{i}_{\text{d}}\left(k+1\right)-i_{\text{d}}\left(k\right)\\ i_{\text{q}}\left(k+1\right)-i_{\text{q}}\left(k\right)\end{array}\right]=\left[\begin{array}{cc}0& \omega T_{\text{s}}\\ -\omega T_{\text{s}}& 0\end{array}\right]\left[\begin{array}{l}{i}_{\text{d}}\left(k\right)\\ i_{\text{q}}\left(k\right)\end{array}\right]+\left[\begin{array}{cc}\frac{T_{\text{s}}}{L}& 0\\ 0& \frac{T_{\text{s}}}{L}\end{array}\right]\left[\begin{array}{l}{e}_{\text{d}}\left(k\right)-u_{\text{d}}\left(k\right)\\ e_{\text{q}}\left(k\right)-u_{\text{q}}\left(k\right)\end{array}\right]$ (9)

整理上式(9)有：

$\left[\begin{array}{l}{u}_{\text{d}}\left(k\right)\\ u_{\text{q}}\left(k\right)\end{array}\right]=\left[\begin{array}{l}{e}_{\text{d}}\left(k\right)\\ e_{\text{q}}\left(k\right)\end{array}\right]+\left[\begin{array}{cc}0& \omega L\\ -\omega L& 0\end{array}\right]\left[\begin{array}{l}{i}_{\text{d}}\left(k\right)\\ i_{\text{q}}\left(k\right)\end{array}\right]-\left[\begin{array}{cc}\frac{L}{T_{\text{s}}}& 0\\ 0& \frac{L}{T_{\text{s}}}\end{array}\right]\left[\begin{array}{l}{i}_{\text{d}}\left(k+1\right)-i_{\text{d}}\left(k\right)\\ i_{\text{q}}\left(k+1\right)-i_{\text{q}}\left(k\right)\end{array}\right]$ (10)

式中 $i_{\text{d}}\left(k+1\right)$ 和 $i_{\text{q}}\left(k+\text{1}\right)$ 为第k + 1时刻系统分别在d轴和q轴上的电流分量 [9]。

根据上式(10)即可对系统的电流内环控制实现无差拍控制，由式(10)可知对下一时刻的d轴和q轴电流分量的预测，直接影响控制效果。在对下一时刻进行预测时，由于控制频率较高可以使用平推预测方案，所谓平推预测其实就是认为 $i_{\text{d}}\left(k+1\right)=i_{\text{d}}^{\ast }\left(k\right)$ 和 $i_{\text{q}}\left(k+1\right)=i_{\text{q}}^{\ast }\left(k\right)$ ，由此产生的预测周期误差可以忽略。电压外环仍采用典型的PI控制策略，因此在平推预测的基础上根据式(10)有如下控制框图3：

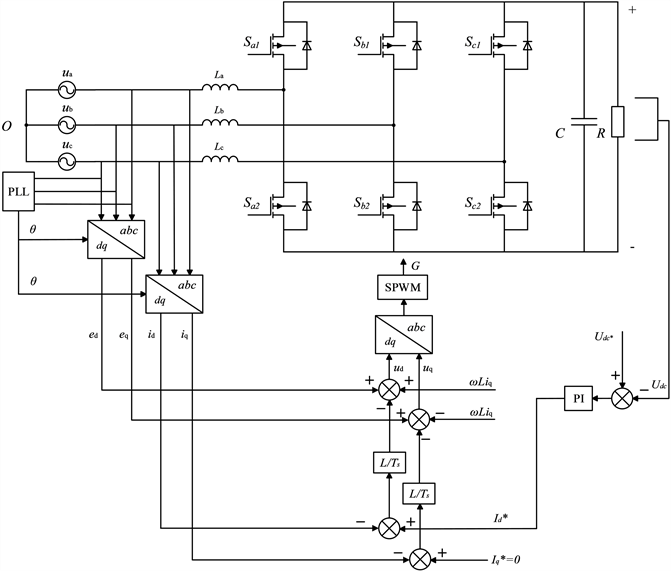
Figure 3. Block diagram of converter system based on deadbeat current control

图3. 基于无差拍电流控制的变换器系统框图

4. 仿真验证

为验证所提出控制方式可行性，按照图3控制方式在MATLAB/SIMULINK中构建系统仿真模型进行仿真验证 [10]，本系统通过无差拍控制器对电流进行控制，其中三相交流输入电压220 V，直流输出电压650 V，控制频率及开关频率均为50 kHz，输入电感L = 0.6 mH，输出电容1000 μF，在纯阻性负载下进行仿真。

4.1. 系统的稳态特性

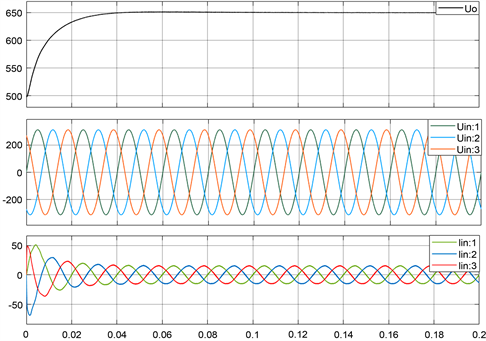
图4为额定功率启动时系统直流输出稳态特性，直流电压上升期间波形无明显超调，经0.08 s后输出电压稳定在650 V，稳态下的直流输出电压波动约为±0.1 V，验证了电压外环调整效果稳定。三相输入电流经30 ms调整后呈规则正弦波，相位跟随输入电压相位，稳态功率因数高达0.99，实现了功率因数校正。

4.2. 系统的负载特性

图5为半载条件启动至稳定运行，在0.25 s处突加负载至满载的负载特性波形图，输出电压波形如图所示。当负载由半载突然增加至满载时，输出直流电压跌落至627 V，经0.12 s调整后，输出直流电压恢复至设定650 V稳定输出。图6为网侧c相电压、电流波形，为方便观察将电流值放大4倍。由图5和图6可以看出，输入电流在负载突增后有一定畸变，但没有电流过冲现象，经一个交流输入周期后，输入电流调整至平稳正弦，相位与输入电压相位相同。

(a)(b)

Figure 4. (a) Rated power waveform under deadbeat control; (b) DC output fluctuation at rated power steady state under deadbeat control

图4. (a) 无差拍控制下额定功率波形；(b) 无差拍控制下额定功率稳态时直流输出波动情况

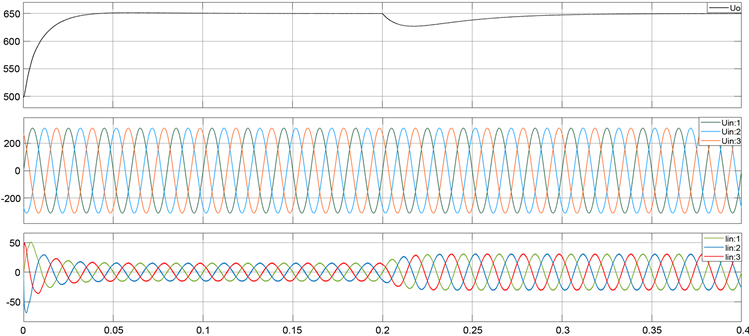
Figure 5. System waveform when load suddenly increases under deadbeat control

图5. 无差拍控制下负载突增时系统波形

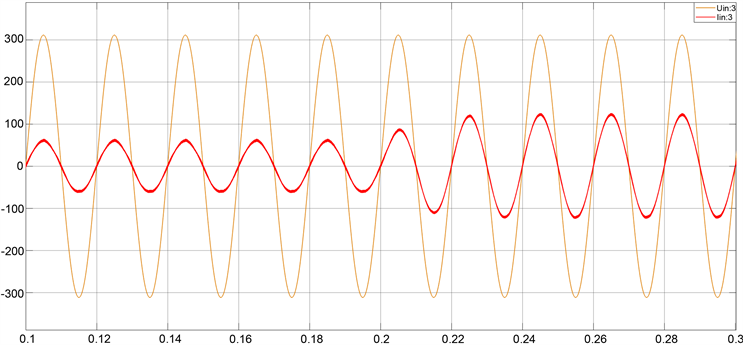
Figure 6. Single-phase input characteristics of system when load suddenly increases under deadbeat control

图6. 无差拍控制下负载突增时系统单相输入特性

图7为满载条件启动至稳定运行，在0.25 s处突降负载至半载的负载特性波形图，输出电压波形如图所示。当负载由满载突然降低至半载时，输出直流电压上升至674 V，经0.12 s调整，输出直流电压恢复至设定650 V稳定输出。图8为网侧c相电压、电流波形，为方便观察将电流值放大4倍。由图7和图8可以看出，输入电流在负载突降后有一定畸变，但没有电流过冲现象，经一个交流输入周期后，输入电流调整至平稳正弦，相位与输入电压相位相同。

由上述仿真结果可得，负载突变过程中，系统输出电压能在6个工频周期内重新进入稳定状态，快速稳定的保证输出恒定。同时由于无差拍控制算法的预测作用，抑制了系统电压波动对环路补偿性能的影响，电流波动较小，输入电流可快速调节并跟随输入电压信号，保证网侧电流正弦化，实现功率因数校正。说明了应用无差拍控制策略的电流内环具有良好的动态响应能力，验证了该控制方案的正确性和可行性。

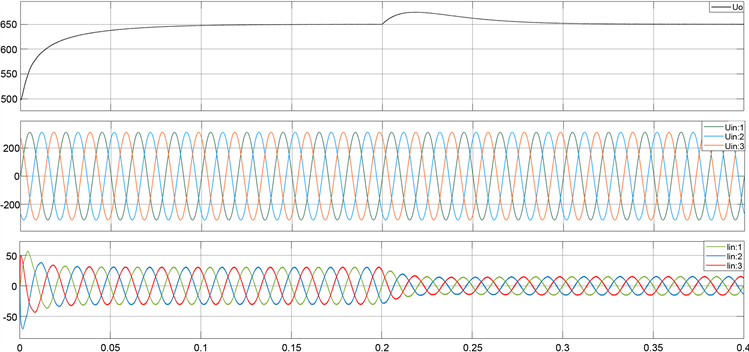
Figure 7. System waveform when load suddenly decreases under deadbeat control

图7. 无差拍控制下负载突降时系统波形

Figure 8. Single-phase input characteristics of system when load suddenly decreases under deadbeat control

图8. 无差拍控制下负载突降时系统单相输入特性

5. 结论

本文在推导了三相六开关PFC整流器在两相旋转坐标系的等效数学模型基础上，引入无差拍控制策略，基于该策略设计了电流内环控制器，并通过MATLAB/SIMULINK进行仿真验证，仿真结果表明，在稳态或负载突变条件下，输入电流均能够快速稳定的跟随输入电压，实现功率因数校正，该控制策略在三相六开关整流器中具有良好的稳态特性和负载特性，验证了无差拍控制策略在该拓扑中应用的可行性，对后续研究具有指导意义。

基金项目

基于电力电子器件的高性能充电系统关键技术(2018YFB0106300)。