1. 交叉数的研究进展
近代图论中发展了图的交叉数这一概念,交叉数是图论中的重要分支,起源于上个世纪五十年代Turan [1] 遇到的砖厂运砖这一实际问题,一经提出,不断吸引国内外众多学者研究,研究图的交叉数问题不仅在拓扑图论研究中具有不可替代的作用,同时在其它学科领域也有重要的应用,如生物工程DNA的图示,电子线路板设计的布线等。由于图的自身结构复杂,对于具体图类的研究绝非易事,Garey,Johnson [2] 已经证实证明图的交叉数问题是一个NP-完全问题,至今,国内外也进行了许多研究,主要研究成果如下。
1.1. 完全图
上个世纪七十年代,R.K. Guy [3] 首次在文献中提出关于完全图
的猜想:对于任意的
,有
对任意实数x,
表示不超过x的最大整数。
1969年R.K. Guy [4] 对
进行了验证,目前的最优结果对于
上面公式成立。
Blazek,Koman等人 [5] 在60年代中期的研究表明上述公式给出的是完全图
的交叉数的一个上界。即:
1970年根据Kleitman [6] 的关于完全二分图的交叉数的结果,对足够大的n有如下的公式成立:
Richter等人得到了
与
的关系 [7] [8] :
2002年Alcholzer,Aurenhammer和Krasser [9] 利用计算机穷举方法证明了
和
的交叉数分别为100和150,并给出了
的交叉数为229。
1.2. 广义Petersen图
不少学者就广义Petersen图进行了广泛的研究,最早于1981年,Exoo,Harary和Kabel [10] 证明了:
1986年Fiorini [11] 对广义Petersen图的交叉数进行研究,计算出当
时所有图
的交叉数的具体值,然而Fiorini的证明存在错误。对于
给出了的数学证明,确定了
,并且
2002年,Richter [12] 和Sarazin指出Fiorini在证明
的交叉数的下界时有漏洞,并以
,
,
为起点,用数学归纳法重新证明并对其结论进行了更正:
2004年,林晓惠 [13] 在其论文中得出了
等部分广义Petersen图的交叉数的上界。
2005年,马登举 [14] 等人得到了广义Petersen图
的交叉数。
2009年,杨元生 [15] 等人利用算法给出了
时
的交叉数的精确值。
Fiorini和黄元秋 [16] 等人分别用不同方法证明了
的交叉数。
2012年,周进鑫、冯衍全 [17] 在广义Petersen图的基础上,首次提出双广义Petersen图的概念,并随后证明了双广义Petersen图不是点传递图。
2013年,郑百功 [18] 在硕士论文中总结了其子图画法的一些性质并给出一种新的对偶图的定义,进而按照这种对偶图的不同情况证明了
的交叉数的精确值为6。
2. 双广义Petersen图DP(7,1)的交叉数
2.1. 双广义Petersen图DP(7,1)
令双广义Petersen图DP(7,1)的顶点集与边集分别为:
;
。由于双广义Petersen图DP(7,1)是一个简单图,记为G。图G的一个分解是子图的列表,使得图G中的每一条都恰好在其中的一个子图中。
将图G的边集分为7个互不相交的子集,令
的顶点集与边集分别表示为
,
,
,可得到
为图G的一个可传递分解。
用
表示在画法D下与
相关的交叉点数目的函数,如下:
令D为双广义Petersen图DP(7,1)的一个好的画法,在画法D下的交叉数以
或者
表示。对于DP(7,1)的给定画法D,
令
与
分别表示圈
与圈
,
。令
,
是
诱导DP(7,1)的子图,
且
,
。
若
,令c为一个正实数,若存在一个正整数
满足
,则令
为使得
成立的
的最小值,反之若这样的
不存在,则
。
Jordan曲线定理任意一条简单(不自交)闭曲线J把平面分成两个区域,在不同区域的两点若要相连,则连结的弧必定与J相交。
根据Jordan曲线定理,则有以下引理:
引理2.1 在图G中,若C与
为两个顶点不相交的圈,
为t阶路径且
,假设D是图G的一个好的画法,若
与
位于
所在区域边界划分平面的相同区域,则
为偶数;反之若
与
位于
所在区域边界划分平面的不同区域,那么
为奇数,后述记为引理2。
2.2. 双广义Petersen图DP(7,1)的交叉数上界
引理2.2 对于双广义Petersen图DP(7,1)的一个好的画法D,存在
。
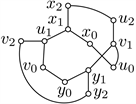
证明:如图1所示,给出了双广义Petersen图DP(7,1)的一个好的画法

Figure 1. A good drawing of DP(7,1)
图1. DP(7,1)的一个好的画法
2.3. 双广义Petersen图DP(7,1)的交叉数下界
假设D为双广义Petersen图DP(7,1)的一个好的画法,由引理2.2可知
。若
,这里将
简记为
,显然
为
的一个子图。
引理2.3
,
。
引理2.4 若
,
,则
。
证明:反证法,不失一般性,假设
,由于
,则
,
,
。由
且
,则
且
。根据
,则
。在画法D中,若
相交叉于
,则由引理2可知
,与
相矛盾,因此
。
假设
,根据
,则
一定被交叉。不失一般性,假设在
中
被交叉,由于
且D是一个好的画法,则
。由引理2可知
与
在
所在区域边界划分平面的不同区域,因此路径
相交于
至少一次,则在D中
至少被交叉三次。又由引理2.3可知
,因此由于
,那么路径
或
相交于
一次,则
。
由于
,
且
,则
。由于
且
,则
分别同构于图2(a),图2(b)。若
同构于图2(a),由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾。若
同构于图2(b),由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾,因此由于
且
,则
。
由于
且
,不失一般性,假设在
中
被交叉,若
,则
分别同构于图2(c)~(e)。若
同构于图2(c),由引理2可知路径
,
同时相交于
,
至少各产生两个交叉,与
相矛盾。若
同构于图2(d),由引理2可知路径
,
同时相交于
,
至少各产生两个交叉,与
相矛盾。若
同构于图2(e),由引理2可知路径
,
同时相交于
,
至少各产生两个交叉,与
相矛盾,因此
。由于
,若
与
在
划分平面的不同区域,由引理2可知路径
,
相交于
至少各产生一个交叉。又由引理2.3可知
且
,则
,产生矛盾,因此
与
在
划分平面的相同区域。若
与
在
划分平面的不同区域,由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾,因此
与
在
划分平面的相同区域。则
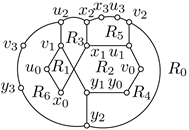
分别同构于图3(a)~(d)。
 (a)
(a)  (b)
(b)  (c)
(c)  (d)
(d)
Figure 3. Good drawings of
with
图3.
在
下的好的画法
若
同构于图3(a),由引理2可知路径
,
,
相交于
至少各产生一个交叉。由引理2.3可知
,则路径
,
或
最多交叉于
或者
一次,与
相矛盾。
若
同构于图3(b),由引理2可知路径
,
相交于
至少各产生一个交叉,由于
,则
。由引理2可知,若
与
位于
划分平面的不同区域,则路径
,
相交于
至少各产生一个交叉,与
相矛盾,因此
与
位于
划分平面的相同区域,由引理2可知若
相交于
至少产生两个交叉,与
相矛盾,则
。同理可证,
,则
同构于图4(a)。如图4(a)所示,由引理2可知路径
,
相交于
,由引理2可知若路径
相交于
,则路径
相交于
至少两次,若路径
相交于
,情形一致。又由于
可知
被路径
或
交叉最多一次,因此路径
,
相交于
至少产生三个交叉。若路径
相交于
可知
,
在区域
,
或
中,由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾,则路径
相交于
。若路径
相交于
,根据引理2可知
,
在区域
,
或
中,由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾。
若
同构于图3(c),由引理2可知路径
,
,
相交于
至少各产生一个交叉。由引理2.3可知
,则路径
,
或
最多交叉于
或者
一次,与
相矛盾。
若
同构于图3(d),由引理2可知路径
,
相交于
至少各产生一个交叉,由于
,则
。由引理2可知,若
与
位于
划分平面的不同区域,则路径
,
相交于
至少各产生一个交叉,与
相矛盾,因此
与
位于
划分平面的相同区域,由引理2可知若
相交于
至少产生两个交叉,与
相矛盾,则
。同理可证,
,则
同构于图4(b)。如图4(b)所示,由引理2可知路径
,
相交于
,由引理2可知若路径
相交于
,则路径
相交于
至少两次,若路径
相交于
,情形一致。又由于
可知
被路径
或
交叉最多一次,因此路径
,
相交于
至少产生三个交叉。若路径
相交于
可知
,
在区域
,
或
中,由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾,则路径
相交于
。若路径
相交于
,根据引理2可知
,
在区域
,
或
中,由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾,则
。
 (a)
(a) 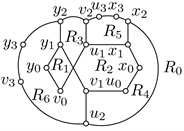 (b)
(b)
Figure 4. Good drawing of
图4.
的好的画法
引理2.5 若
,
,
且
,则
同构于图5中的一个图。
证明:由于
,得到
,
,
。因为
和
,则
。由
,不失一般性令
。由于
且
,那么
和
位于
划分平面的同一区域,
和
位于
划分平面的同一区域。根据引理2可知,若
与
位于
划分平面的不同区域,则路径
交
至少产生一个交叉,路径
交
至少产生一个交叉,与
相矛盾,所以
与
位于
划分平面的同一区域。根据引理2可知
。又由好的画法的定义可知
只能相交于
,
或
,则
同构于图5中的一个图。
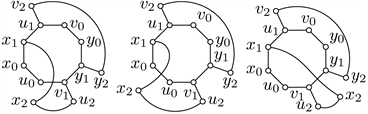 (a) (b) (c)
(a) (b) (c)
Figure 5. A good drawing of
if
crosses
图5.
在
交
下的一个好的画法
引理2.6 令D是一个好的画法,若
且
同构于图5(a),则
。
证明:反证法,假设
。由于
,得到
,
,
,
,
。
如图5(a)所示,由引理2可知路径
,
交叉于
,则
的边被交叉至少两次。又由于
,则
。若
与
位于
划分平面的不同区域,由引理2可知路径
,
相交于
至少各产生一个交叉,与
相矛盾,则
与
位于
划分平面的同一区域。若
相交于
,由引理2可知
的边被交叉至少两次,与
相矛盾,则
。
同构于图6(a)。如图6(a)所示,根据引理2可知路径
相交于
,若
相交于
,由引理2可知
相交于
至少产生两个交叉。同理
相交于
的情形完全一致。又由
可知
被路径
或
交叉至多一次,从而路径
,
相交于
至少三次。由
,可以得到
和
,则
同构于图6(b)。
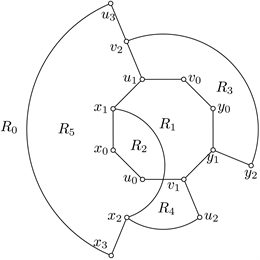 (a)
(a)  (b)
(b) 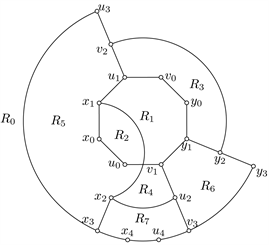 (c)
(c) 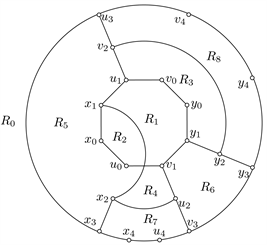 (d)
(d)
Figure 6. Sub-drawings from D with
crosses
图6. 在
交
下D的子画法
如图6(b)所示,若
与
位于
划分平面的不同区域,由引理2可知路径
,
交于
至少各产生一个交叉,与
相矛盾,则
与
位于
划分平面的同一区域。如果
交叉于
,由引理2可知
的边被交叉至少两次,与
相矛盾,因此
。又由于
,则
,
。
同构于图6(c)。
如图6(c)所示,由引理2可知路径
,
相交于
至少产生三个交叉,又由
可知
和
。若
相交于
,由引理2.2可知
所在的圈
交于圈
至少产生两个交叉,与
相矛盾,因此
。若
和
位于
划分平面的不同区域,由引理2可知路径
,
交叉于
,则
的边被交叉至少两次,与
相矛盾,则
与
位于
划分平面的同一区域。如果
相交于
,由引理2可知
的边被交叉至少两次,与
相矛盾,则
。
同构于图6(d)。如图6(d)所示,由引理2可知路径
相交于
至少产生一个交叉,路径
,
相交于
至少各产生两个交叉,因此对于D有
。由假设
,则
,由引理2可知路径
相交于
产生一个交叉,路径
,
相交于
各产生两个交叉。由引理2可知
交叉于
,则
在区域
,
或
中,下面分为三种情形讨论。
情形1:若
在区域
中,由引理2可知
交叉于
,则
在区域
,
或
中。若
在区域
中,由引理2可知若
相交于
,则
同构于图7(a)。若
相交于
,则
同构于图7(b)。若
在区域
中,由引理2可知
相交于
,则
同构于图7(c)。若
在区域
中,由引理2可知
相交于
,则
同构于图7(d)。如图7所示,由
可知
干净,则
在区域
或
中。由
在区域
或
中,根据引理2可知路径
都交于
至少产生三个交叉。
 (a)
(a) 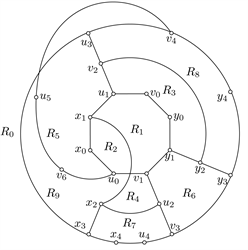 (b)
(b) 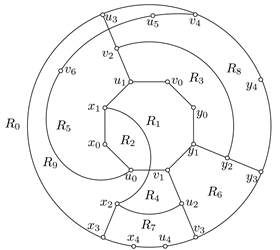 (c)
(c)  (d)
(d)
Figure 7. A good drawing of
图7.
的一个好的画法
情形2:若
在区域
中,则
同构于图8(a)。如图8(a)所示,由于
可知
干净,则
在区域
或
中。由
在区域
或
中,根据引理2可知路径
相交于
至少产生三个交叉。
情形3:若
在区域
中,则
同构于图8(b)。如图8(b)所示,由于
可知
干净,则
在区域
或
中。由
在区域
或
中,根据引理2可知路径
相交于
至少产生三个交叉。
 (a)
(a)  (b)
(b)
Figure 8. A good drawing of
图8.
的一个好的画法
3. 结论
本文主要证明图DP(7,1)的交叉数,给出交叉数为7的一个好的画法。近一步通过反证法证明了交叉数的下界,最终证明了图DP(7,1)在
,
且
下的交叉数为7。对于双广义Petersen图
,
,证明了归纳基础
,对于图
,
交叉数将是下一步继续研究的内容。