1. 引言
钛合金(TC4)是一种难加工材料,具有材质较轻、强度硬度高、耐热性强、抗腐蚀性好等优点 [1] 。这些材料优势使钛合金被广泛应用于航空航天领域,例如用于制造喷气发动机的压气机或叶片、机匣等 [2] 。TC4也是一种难加工材料,具有导热系数小、切削温度高、硬度较大等特点,加工性能差,但车削工艺可以有效解决TC4的加工难题,而超声振动辅助车削作为一种新工艺,还可以有效提高TC4加工表面的表面完整性 [3] 。在车削加工中施加超声振动后,刀具的有效切削时间被缩短,这有利于减小切削力、降低切削热,从而提高工件的表面加工质量 [4] 。超声振动辅助车削加工的应用已经普及,庞宇等 [5] 在用车削工艺加工TC4时,通过采用给主切削方向加载超声振动的方式,发现相对于传统车削加工,切削力降低了15%,切削温度下降了10.4%;胡智特等 [6] 研究了超声振动辅助车削加工TC4的加工特性,发现在超声振幅确定、超声频率在20 KHz、振幅为20 μm时,平均切削力相对于传统车削加工降低了24%。上述学者的结论主要来源于试验验证。在理论研究与仿真验证方面,冷超群等 [7] 利用ABAQUS软件对超声振动辅助车削加工的过程做了仿真分析,发现在超声振动辅助条件下,刀具前刀面温度有明显下降,平均切削力数值较小;路冬等 [8] 基于ALE方法对TC4的超声振动车削过程进行模拟,发现在一个振动周期内,刀具与工件、切屑在很长时间内处于分离状态,这种分离特性有效降低了切削力和切削温度;Zhang C等 [9] 结合超声振动辅助车削加工硬脆材料试验,证明超声振动条件不仅有利于车削加工金属合金,也有利于车削加工硬脆陶瓷材料;Jiao L等 [10] 在ABAQUS软件中采用Johnson-Cook本构模型,通过切削仿真证明了超声振动辅助条件有利于降低车削力和车削温度;Overcash J L等 [11] 通过有限元仿真试验,发现超声振动辅助车削条件下,车刀前刀面温度处于动态变化,散热稳定,证明超声振动条件有利于抑制刀具氧化磨损。
本文选择研究的刀具材料为硬质合金(YG8),试切材料为钛合金(TC4),基于振动学理论,建立了一种表征传统车削振动系统的解析解,并使用ABAQUS软件建立了二维车削有限元分析模型,开展了传统车削与超声振动辅助车削两种工艺的TC4切削仿真模拟。仿真结果表明,当超声振幅在4 μm~12 μm内时,超声振动辅助车削加工相较于传统车削加工,刀具受到的径向力下降了11.4%~20%,TC4加工表面最大压应力下降了7.8%~19.4%,且加工表面压应力和径向力均随着超声振幅的提高而下降。
2. 车削加工振动系统建模与分析
2.1. 传统车削加工振动系统建模与分析
车削加工时,TC4工件绕主轴高速旋转,车刀从工件外圆面沿径向切入给定深度后,会沿着进给方向缓慢运动,此时车刀刀尖的受力分析如图1所示。车刀刀尖受到的合力为
,其中,径向力
、主切削力
和进给阻力
分别与切削深度、工件转速和进给速度有关。由于
、
和
在车削加工过程中一直存在,因此车刀在这三个力的方向上都存在振动情况,故本文以车刀刀尖为坐标系原点,建立了一种表征车刀振动情况的数学模型。
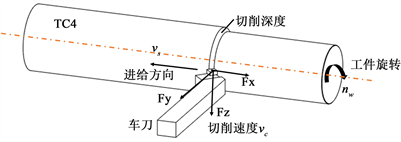
Figure 1. Schematic diagram of force analysis of turning tool tip
图1. 车刀刀尖受力分析示意图
假设在
平面内不考虑
,则刀具在
平面内存在水平移动和定轴转动两种运动状态,如图2(a)所示。在
作用下,刀具会因振动沿着x坐标轴方向滑移。同时,由于刀具和刀柄之间是轴向定位的,故
还会导致刀具产生微小偏转。同理,如果在
平面内不考虑
,或者在
平面内不考虑
,则刀具在
或
平面内会在
或
的作用下沿着y或z坐标轴方向产生微小位移,如图2(b)和图2(c)所示。但这种情况下,刀具与刀柄之间还存在端面定位,因此本文忽略了此时刀具在
或
平面内的偏转。
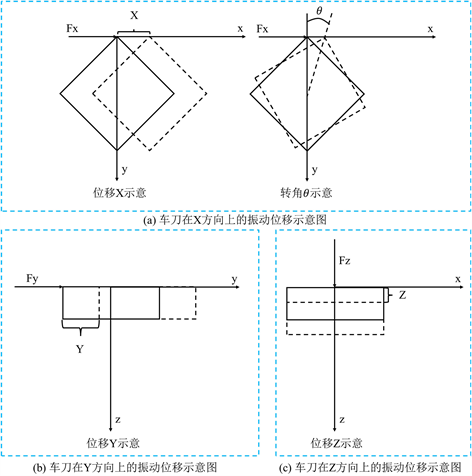
Figure 2. Vibration displacement diagram of turning tool in different directions
图2. 车刀在不同方向上的振动位移示意图
本文假设的车削振动模型具有四个自由度,但每个自由振动方程相互独立,没有形成耦合关系,因此可以分别建立每个自由度的振动平衡方程。假设车刀在每个自由度上的变形分别为X,
,Y,Z。根据弹性力学的小变形假设可知,如果假设刀尖绝对坐标没有改变,则可以近似将X,
,Y,Z视为车刀在四个自由度上的应变 [12] 。此时,车刀刀尖处的二阶偏微分振动平衡方程的矩阵形式为式(1)。
(1)
式(1)中,a和b分别为车刀的宽度(长度)和高度(mm),E为YG8的弹性模量(510 GPa),
为YG8的密度(14.5 g∙cm−3)。若同时令式(1)中的
,则可进一步推导该振动方程下每一个自由度的圆频率,并根据圆频率确定通解形式。式(2)即为刀具在
,
和
平面内的振动方程通解。
(2)
式(2)中,
和
均为通解待定系数。在式(2)的方程组中,每一个参数t前的第一个多项式即为X,
,Y,Z四个参数的振动方程圆频率。根据振动方程特解形式可知:
。因此,将式(2)中每一组方程的圆频率带入
并与式(1)联立,即可推导出式(2)中每一个通解的特解,再结合二阶偏微分方程的解为特解与通解求和的特点,即可确定刀具振动方程的最终结果。式(3)即为本文模型中
,
,
和
的振动方程解析解。
(3)
2.2. 超声振动辅助车削加工振动系统建模与分析
在刀具的进给方向施加超声振动载荷的示意图如图3(a)所示。施加超声振动载荷后,刀具的滑移和偏转幅度(
,
)也减小。这是因为超声振动载荷频率较高,所以在单位时间内,合阻力会在数值上会反复由
变化为
,此时进给方向合阻力下降,对车削加工产生有利影响。在刀具的主切削力方向施加超声振动载荷的示意图如图3(b)所示。此时刀具的滑移幅度(
)增大。这是因为在主切削力方向上,超声振动载荷与主切削力叠加,使合力增大。提高主切削力依然有利于车削加工。在刀具的吃刀方向施加超声振动载荷的示意图如图3(c)所示,此时刀具的滑移幅度(
)增大。这是因为车刀的前刀面和加工表面之间因为相互作用在径向产生了较大的
,而后施加的超声振动载荷还会与
叠加,使径向力更大,振动更剧烈,这会导致工件产生挠度,降低车削加工精度。因此,在刀具的吃刀方向施加超声振动载荷会产生不利影响。
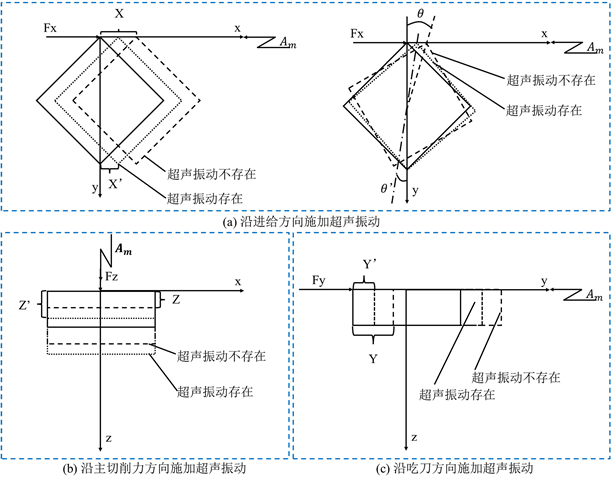
Figure 3. Schema of applying ultrasonic vibration load in different directions
图3. 在不同方向上施加超声振动载荷示意图
假设施加的超声振动载荷振幅为
;频率为
;初相为
,则表征该超声振动载荷的多项式为
。假设超声振动载荷增益在数值上为
,在进给方向上的合力为
,在主切削力方向上的合力为
,则联立式(3)即可推导施加超声振动载荷后的车刀受力和振动模型。式(4)为仅在进给方向或仅在主切削力方向施加超声振动载荷后的车刀受力方程,式(5)和式(6)分别为仅在进给方向或仅在主切削力方向施加超声振动载荷后的车刀振动方程。
(4)
式(4)中,t为时间常数(s)。本文对式(4)进行了定性分析,其中
与
两种车刀受力情况的变化波形示意图如图4所示。根据图4(a)可知,在进给方向,
的最大值就是
,在施加超声振动载荷后,
会在区间内衰减。由于超声振动频率很高,所以
的变化周期很短。在这种情况下,
作用时间短,对加工产生不利影响的时间相较于传统车削有明显下降。另外,根据图4(b)可知,在主切削力方向,
的最大值是
,在超声振动载荷作用下,此时的主切削力相较于传统车削加工增大,从而有利于车削加工。
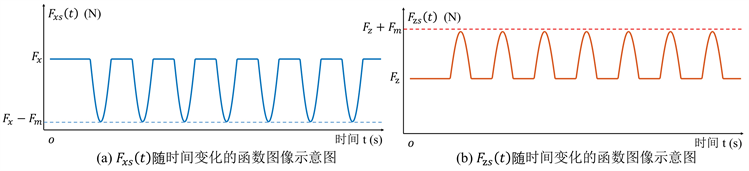
Figure 4. Fluctuation diagram about
and
图4.
与
波动示意图
(5)
在式(5)中,
和
分别表示刀具在超声振动载荷作用下,沿着
方向的位移和绕轴转动的偏转角。经推导,位移的最小值为
,偏转角的最小值为
,且都在数值上相较于传统车削加工有所下降。此时,刀具在进给方向的阻力降低,有利于提高车削加工效率,降低刀具磨损。
(6)
在式(6)中,
表示刀具在超声振动载荷作用下沿着
方向的位移,最大值为
,在数值上相较于传统车削加工有所上升。在这种情况下,刀具因高速振动频繁离开工件表面,既容易加快刀具散热,又容易使切屑与前刀面分离,提高加工表面质量并降低刀具磨损。同时,主切削力增大也有利于提高车削加工效率。
3. 有限元仿真与对比
3.1. 传统车削仿真研究
本文采用ANSYSAPDL软件了分析车刀和工件的模态,研究了车刀和工件的振动特性。仿真时采用的建模参数统计在表1中。车刀的有限元模型及其模态响应仿真如图5所示。仿真时,本文取车刀的最高阶模态为九阶模态,并在做车刀的谐响应仿真分析时将边界条件限定在车刀刀尖上。仿真结果显示,在车削过程中,刀具的压应力集中在刀尖附近,而且刀具会发生微小位移。

Table 1. Modeling and simulation parameter table [13]
表1. 建模与仿真参数表 [13]

Figure 5. Finite element analysis diagram of turning tool
图5. 车刀有限元分析示意图
工件的有限元模型及模态响应仿真如图6所示。本文只取了工件的第一和第二阶模态做研究对象,并基于工件受力情况进行了谐响应仿真分析。在该仿真模拟中,工件的边界条件为一端施加扭矩,一端固定,节点力施加在工件母线上的随机位置。仿真结果显示,在车削加工过程中,工件会发生弯曲。这是因为工件会因为车刀的反作用力产生挠曲度,并且工件的压应力会集中在切削点(刀尖)附近。

Figure 6. TC4 finite element analysis diagram
图6. TC4有限元分析示意图
本文还采用ABAQUS软件对传统车削加工TC4的材料去除过程进行了有限元仿真。该仿真磨削采用了Johnson-Cook各向同性本构模型,在仿真参数设定中,分析步分辨率为0.012 s,分析步数为20步。基于上述参数,得到的传统车削加工仿真的应力云图如图7所示。该仿真结果表明,TC4的切屑类型为崩碎屑,车削加工的压应力集中在切削点(刀尖)附近,而且加工过后的工件表面存在残余压应力。
3.2. 超声振动辅助车削仿真研究与对比
本文还采用ABAQUS软件对超声振动辅助车削加工TC4的过程进行了有限元仿真,传统车削加工与超声振动辅助车削加工的切削仿真对比图如图8所示。在切削仿真模拟中,建模示意图与网格划分示意图如图8(b)和图8(c)所示,超声振动载荷施加在刀具的刚性节点上(节点位置如图8(c)中刀具上的叉形标记所示)。对比发现,传统车削加工的最大表面压应力为1543 σzs,而当超声振幅在4 μm~12 μm的区间内时,加工表面最大压应力为1423 σzs~1243 σzs,下降了7.8%~19.4%。与传统车削相比,超声振动辅助车削加工有利于降低工件加工表面残余应力,提高加工表面完整性。
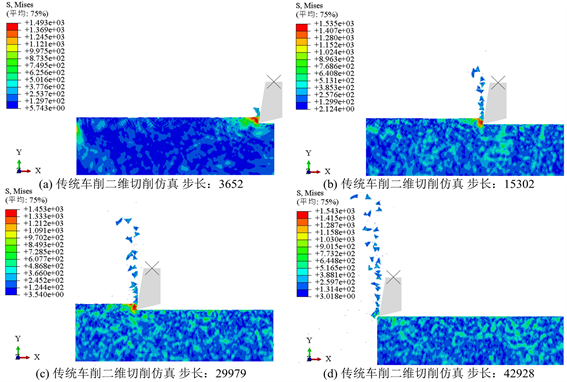
Figure 7. Traditional turning two-dimensional cutting simulation
图7. 传统车削二维切削仿真模拟

Figure 8. Simulation and comparison of traditional turning and ultrasonic vibration assisted turning
图8. 传统车削与超声振动辅助车削仿真模拟与对比
传统车削加工与超声振动辅助车削加工的径向力对比图如图9所示。对比发现,传统车削加工最大径向力约为35 N,而当超声振幅在4 μm~12 μm的区间内时,径向力分别约为31 N,29 N和28 N,下降了11.4%~20%。与传统车削相比,超声振动辅助车削加工时,刀具受到的径向力下降明显,有利于提升加工表面的表面完整性,提升加工效率以及降低刀具磨损。
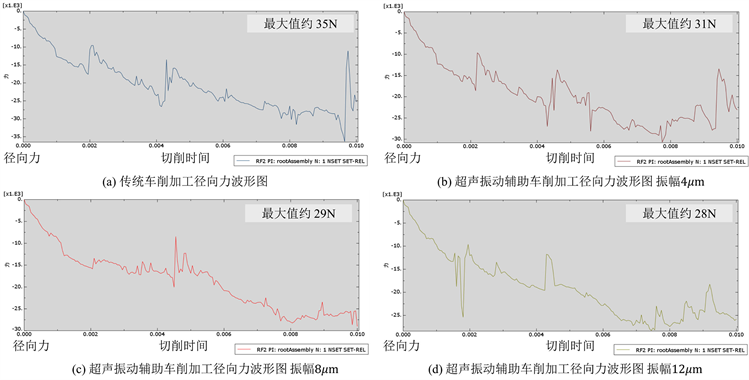
Figure 9. Comparison of radial force waveforms between traditional turning and ultrasonic vibration assisted turning
图9. 传统车削与超声振动辅助车削径向力波形对比
4. 结果与讨论
本文基于振动学理论,建立了一种表征传统车削振动系统的解析模型,定性分析了刀具在车削过程中的微小位移变化和受力变化情况。
本文采用ANSYS APDL软件对超声振动辅助车削加工条件下的车刀与TC4进行了模态分析和谐响应分析。仿真结果表明,在车削过程中,刀具的压应力集中在刀尖附近,而且刀具会产生微小形变。另外,工件会因为车刀的反作用力产生挠曲度,并且工件的压应力会集中在切削点附近。
本文采用ABAQUS软件分析了超声振动对车削加工的影响并做了试验对比。仿真结果表明,当超声振幅在4 μm~12 μm内时,超声振动辅助车削加工相较于传统车削加工,刀具受到的径向力下降了11.4%~20%,TC4加工表面最大压应力下降了7.8%~19.4%,且加工表面压应力和径向力均随着超声振幅的提高而下降。