1. 引言
蜂窝构件具有截面形式合理、抗弯刚度大、承载力高、便于布置管线等特点,相比于相同力学性能的实腹构件,蜂窝构件可节约钢材25%~30%,节省防护涂料与运输安装费用15%~30%,因此蜂窝式钢构件广泛应用于高层建筑、工业厂房、大跨度空间结构、桥梁工程、船舶工程等实际工程中 [1] [2] 。长期以来,国内外学者已经对蜂窝构件的强度、刚度及稳定性进行了深入研究。徐晓霞等 [3] 通过有限元软件研究了腹板开六边形孔的压弯蜂窝钢柱在弯矩平面内的极限承载力,并分析了长细比、开孔率、偏心距等参数对承载力的影响。贾连光等 [4] 对四个压弯蜂窝钢柱进行了试验研究,发现扩张比K = 1.5的蜂窝式压弯钢柱较原实腹式柱极限承载力有大幅度提高。Sweedan等 [5] 通过ANSYS软件分析了在轴心荷载作用下,对圆形、六边形孔的蜂窝钢柱绕强轴的整体屈曲,并得到了弹性屈曲荷载。王燕 [6] 通过有限元软件研究了蜂窝钢柱绕强轴的稳定性,在有、无残余应力时,腹板开圆孔、六边形孔和八边形孔蜂窝钢柱在轴心、偏心荷载作用下的极限稳定承载力进行了研究,并分别对规范给出的轴压实腹柱稳定公式、偏压实腹柱稳定公式进行了修正。张雯 [7] 通过有限元软件验证了蜂窝钢柱平面内整体稳定计算公式,并提出扩张比处于1.4至1.5之间的构件稳定承载力达到了最大值,而换算长细比最小,经济效果更好。贾连光等 [8] 研究蜂窝式偏心受压构件腹板局部稳定性能,得到蜂窝式偏心受压构件腹板高厚比限值。林庆捷等 [9] 对焊接H型钢蜂窝短柱进行轴压试验,并分析了孔洞的直径及边孔孔心至柱端距离对蜂窝短柱轴压承载力、刚度和延性的影响,对于翼缘较薄的试件,腹板厚度对破坏模式有较大的影响,而对于翼缘较厚的试件,试件破坏模式主要与边孔距柱端的距离有关;随着孔径的增大,试件极限承载力略微降低,并提出其极限承载力公式。苏益生等 [10] 运用ANSYS有限元软件对扩张比K = 1.5,腹板开圆孔、六边形孔蜂窝钢柱在轴心、偏心荷载作用下的稳定极限承载力进行了研究,发现比扩张前的实腹式柱承载力要高。目前,对于蜂窝式压弯构件的稳定性研究则刚处于起步阶段,无论是试验研究,还是理论研究,都相对较少,并未写入相关标准中,极大地限制了蜂窝构件在实际工程中的应用。因此,本文将通过数值模拟及理论分析两个方面,对蜂窝式压弯构件的弯矩作用平面内稳定承载力进行了研究,将有限元结果和试验结果进行对比,验证了有限元模型的可靠性,利用ABAQUS有限元软件建立了不同参数的蜂窝式压弯构件模型,分析了不同因素对其稳定承载力的影响。参照现行《钢结构设计标准》 [11] 实腹钢柱的整体稳定公式,基于边缘屈服准则,提出了考虑开孔参数的蜂窝式压弯构件在弯矩作用平面内的整体稳定承载力的计算公式,为工程实际应用提供参考。
2. 有限元模型建立与验证
2.1. 试验简介
文献 [12] 中共设计制作了4根不同长度的蜂窝构件,对试件进行弯矩作用平面内偏心矩为50 mm的轴向集中力加载,钢材种类为Q235B,扩张比(蜂窝构件的截面高度H与原型实腹梁的截面高度h之比) K = 1.5,测得钢材力学性能指标:屈服强度fy = 265 MPa、极限强度fu = 417 MPa、弹性模量E = 205 GPa。原H型钢型号为H100 × 100 × 6 × 8,经过加工后形成了正六边形孔蜂窝构件,截面高度为150 mm,正六边形孔边长为58 mm,对角线长116 mm,相临孔洞之间最小净距离等于正六边形孔边长,即58 mm。在试验过程中,最危险点在试件中点处,此处的弯矩和挠度最大,因此,应变测点布置在试件1/2处的腹板和翼缘上。本次试验采用端部水平轴向静力加载方案,选用油压千斤顶进行加载,试件与千斤顶之间连接有拉压传感器(BLR-1/70T),试验数据通过UCAM-70A数据采集仪采集,加载点在试件中心轴偏下,偏心距为50 mm。试验加载装置见图1,试件尺寸如图2所示。
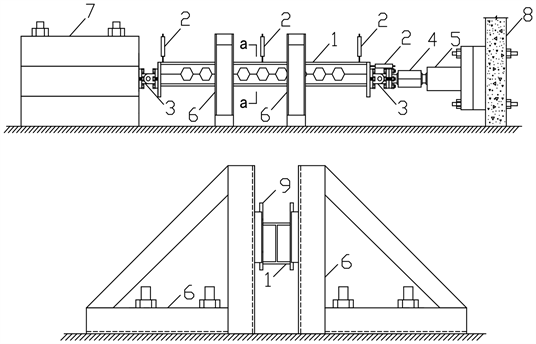 1:试件;2:位移计;3:连接铰;4:传感器;5:千斤顶;6:侧向支撑;7:台座;8:反力墙;9:滑板。
1:试件;2:位移计;3:连接铰;4:传感器;5:千斤顶;6:侧向支撑;7:台座;8:反力墙;9:滑板。
Figure 1. Diagram of experimental loading device
图1. 试验加载装置图
2.2. 网格的划分、单元选择及边界条件
在进行网格划分时,首先对模型整体布种,然后针对形状复杂及跨中的部位釆用“为边布种”细化局部网格,选取以六边形为主的网格形状并采用扫略技术进行划分。有限元模型采用空间三维缩减积分实体单元C3D8R来模拟。本文的模型构件底部中心处设置耦合点,U1 = U2 = U3 = 0,UR2 = UR3 = 0,顶部耦合点设置在距中心点50 mm处,U1 = U2 = 0,UR2 = UR3 = 0,试验中为防止构件发生弯矩作用平面外位移,在模型的两个1/3处分别设置了侧向支撑,通过约束有限元模型在这两处翼缘单元所有节点x方向的线位移来实现。为突出孔洞构造对蜂窝构件受力性能的影响,建模时忽略了焊缝和焊接残余应力的影响。
2.3. 参数确定
试验试件为Q235B钢,钢材本构关系模型采用双折线模型,如图3所示。并遵循Von-Mises屈服准则及其相关的流动法则。有限元模型的截面尺寸为H150 × 100 × 6 × 8,弹性模量为205 GPa,泊松比为0.3,屈服强度为265 Mpa。有限元模型如图4所示。
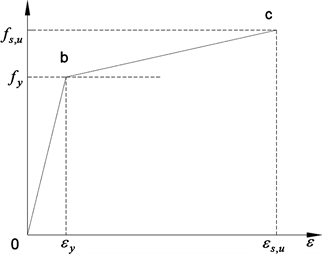
Figure 3. Constitutive relation of steel
图3. 钢材本构关系
2.4. 有限元结果与试验结果对比
试验试件和有限元模型的破坏形态如图5所示,从图5中可看出,二者破坏模式均为蜂窝构件跨中蜂窝孔处形成塑性铰破坏,试验结果与有限元模拟结果吻合较好。试验与有限元模拟的荷载–跨中挠度曲线如图6所示,从图6中可看出,试验的极限承载力为321.7 kN,有限元的极限承载力为312.8 kN,误差仅为2.8%。由于建立有限元模型时忽略了几何缺陷和残余应力等因素,所以有限元结果比试验结果稍低,这说明利用ABAQUS进行实体建模研究蜂窝构件平面内稳定承载力是安全的,验证了本文所建有限元模型的较高的精确性,可以进行下一步参数化分析。

Figure 5. Comparison chart of failure phenomena between test and finite element model
图5. 试验与有限元模型破坏现象对比图
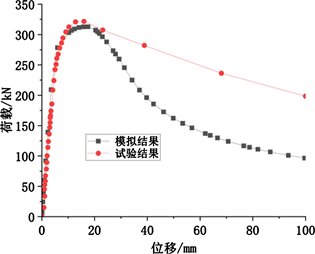
Figure 6. Load-midspan deflection curve
图6. 荷载–跨中挠度曲线
3. 参数化分析
3.1. 模型参数
本文建立了截面尺寸为H150 × 100 × 6 × 8的H型截面的蜂窝构件模型,共建立了24个有限元模型。模型参数见表1。
3.2. 破坏形态分析
构件受力变形直到破坏的过程基本相同,都经历了弹性、弹塑性、塑性阶段。在弹性阶段,荷载–跨中挠度曲线基本呈直线,构件的变形不太明显,继续加载,构件即将达到极限荷载,此时构件处于弹塑性阶段,荷载–跨中挠度曲线变成曲线,当构件到达极限荷载的时候,构件进入塑性阶段,构件突然发生明显弯曲,此时,荷载加不上去而荷载–跨中挠度曲线呈下降段,同时,试件在跨中截面形成塑性铰,构件整体发生弯曲破坏,并且伴随着腹板和下翼缘发生局部鼓曲。有限元结果见表2。取试件1和试件10破坏云图为例,如图7、图8所示。
3.3. 孔型对稳定承载力的影响
通过有限元分析可知,圆形孔、正六边形孔蜂窝构件在开孔数目和开孔率相同时,孔型对蜂窝式压弯构件稳定承载力的削弱作用不同。在相同条件下,圆形孔蜂窝构件的极限稳定承载力要稍高于正六边形孔蜂窝构件的极限稳定承载力,这是由于圆形孔开孔截面连续变化,与六边形孔相比减小了孔角出现应力集中的影响。在开孔率分别为30%、40%、50%、60%、70%时,圆形孔蜂窝构件极限稳定承载力比
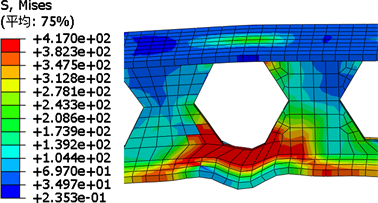
Figure 7. Specimen 5 failure cloud image
图7. 试件5破坏云图
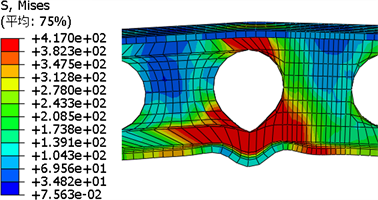
Figure 8. Specimen 6 failure cloud image
图8. 试件10坏云图
正六边形孔蜂窝构件极限稳定承载力分别提高了4.3%、2.0%、3.7%、2.5%、2.4%,且极限稳定承载力下降曲线趋势基本一致。圆形孔与正六边形孔对截面削弱趋势基本一致,对构件的极限承载力的影响差异很小。由图9分析比较可知,2种孔型蜂窝构件极限稳定承载力总体下降趋势基本一致。
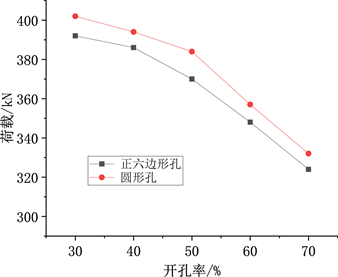
Figure 9. Comparison chart of bearing capacity decline trend of two passes
图9. 两种孔型承载力下降趋势比较图
3.4. 开孔率对稳定承载力的影响
图10、图11是正六边形孔和圆形孔蜂窝构件在相同开孔数目条件下不同开孔率时的荷载–位移曲线图。通过有限元分析可知,随着开孔率增加,蜂窝构件的稳定承载力降低,当开孔率由30%增加的70%时,正六边形孔蜂窝构件的稳定承载力由392 kN降低到324 kN (降低了17.3%);圆形孔蜂窝构件构件的极限稳定承载力从402 kN降低到332 kN (降低了17.4%)。对于正六边形蜂窝构件,当开孔率从30%提高到70%时,开孔率每增加10%,其极限稳定承载力分别降低了1.5%、4.1%、5.9%、6.8%。对于圆形孔蜂窝构件,当开孔率从30%提高到70%时,开孔率每增加10%,其极限稳定承载力分别降低了1.9%、2.5%、7.0%、7.0%,这是由于随着开孔率的增加,导致腹板截面削弱过大,使蜂窝构件的强度下降。其中,六边形的开孔率在30%~40%时,圆形孔的开孔率在30%~50%时,蜂窝构件的极限稳定承载力下降幅度较小。故建议六边形孔蜂窝构件的开孔率在30%~40%之间,圆形孔蜂窝构件的开孔率在30%~50%之间。
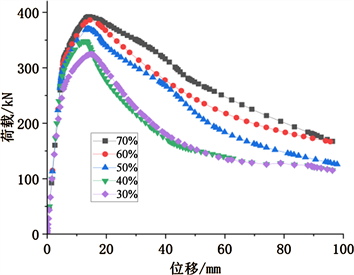
Figure 10. Load-displacement curve of hexagonal castellated beam-columns
图10. 正六边形孔蜂窝构件荷载–位移曲线图
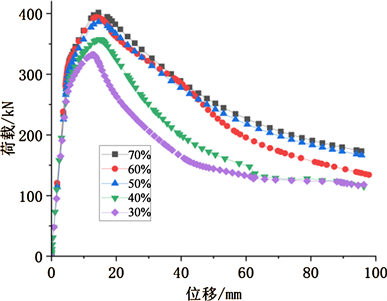
Figure 11. Load-displacement curve of circular castellated beam-columns
图11. 圆形孔蜂窝构件荷载–位移曲线图
所以由图10、图11可得出结论:开孔率对蜂窝式压弯构件的极限稳定承载力影响较明显,蜂窝构件随着开孔率的增大,其极限稳定承载力下降的趋势较为明显。
3.5. 孔间距对稳定承载力的影响
由图12可知,当孔间距从150 mm增加到195 mm,荷载从309 kN提高到320 kN (提高了3.5%),这是由于,当孔间距增加时,蜂窝构件T型板面积增大,并对蜂窝构件的腹板削弱变小使其刚度增加。因此当孔间距增加时,蜂窝式压弯构件的极限稳定承载力提高。
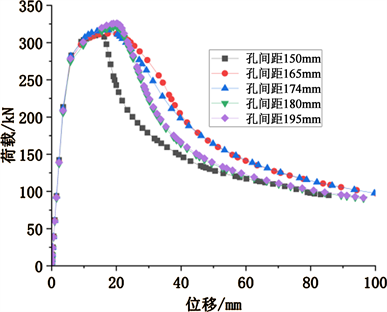
Figure 12. Load-displacement diagram of hole spacing change
图12. 孔间距变化的荷载–位移图
4. 蜂窝式压弯构件稳定承载力计算的验证
压弯构件平面内稳定计算可分为两种计算准则,对于弹性压弯构件,可用截面边缘屈服作为稳定计算的准则,当弯矩绕强轴(x轴)作用时,引入塑性发展系数,蜂窝式压弯构件弯矩作用平面内的稳定性应按下式计算:
(1)
式中:
N——所计算构件范围内的轴心压力(N);
——参数,
,
为蜂窝式压弯构件换算长细比(mm);
——弯矩作用平面内轴心受压构件稳定系数,由
得到,
;
——所计算构件段范围内的最大弯矩设计值(N∙mm);
——在弯矩作用平面内对受压最大纤维的毛截面模量,不考虑孔洞的影响(mm³);
——与截面模量相应的截面塑性发展系数;
——等效弯矩系数,按钢结构设计规范的有关规定选取;
A——所计算构件的横截面面积,不考虑孔洞的影响(mm²);
——钢材的屈服强度(N/mm)。
压弯构件整体弯曲后,沿杆长各截面上会存在弯矩和剪力。对实腹式构件而言,剪力引起的附加变形很小,对应的临界力的影响也很小。因此实腹式压弯构件整体稳定的临界力,仅仅考虑了由弯矩作用所引起的变形,而忽略了剪力所引起的变形。对于蜂窝式压弯构件,发生平面内失稳时,情况有所不同,因腹板并不是连续的板而是每隔一定距离有孔洞。蜂窝式压弯构件的剪切变形较大,因此剪力所造成的附加挠度影响就不能忽略。根据文献 [13] 介绍的格构柱设计中提到,在格构柱的设计中,对虚轴失稳的计算,常以加大长细比的办法来考虑剪切变形的影响。所以本文在研究蜂窝式压弯构件的设计中,对平面内弯曲失稳的计算,同样也以加大长细比的办法来考虑剪切变形对蜂窝构件的影响,加大后的长细比称为换算长细比 [14] 。
根据弹性稳定理论,当考虑剪力的影响后,其临界力为:
(2)
其中,
,在蜂窝式压弯构件中T型截面与翼缘的连接视为刚接,假定变形反弯点在各节点中点。若只考虑翼缘和T型板在横向剪力作用下的弯曲变形,取分离体,可得单位剪力作用下T型板弯曲变形引起的翼缘位移
为:
,翼缘本身弯曲变形时的位移
为
,由此得剪切角r,
,将此r值代入式(2),并令
,
,得换算长细比
为:
。
假设
,
,则
(3)
根据钢结构规范对格构式双肢缀板柱的规定,缀板线刚度之和
应大于6倍的分肢线刚度,即
,若取
,则
,因此式(3)成为:
(4)
式中:
——对应实腹式压弯构件长细比(mm);
——分肢的长细比(mm),
为蜂窝孔间腹板净距离,随着开孔率的逐渐增大其值逐渐减小,
为T型截面绕弱轴的回转半径。
为了验证公式的可靠性,将本文公式的计算结果与10个有限元模拟结果进行对比,公式计算结果与有限元结果见表3。

Table 3. Comparison of finite element results and formula calculation results
表3. 有限元结果与公式计算结果对比
通过上表可知,有限元结果与理论公式结果较为吻合,本文公式计算结果与有限元结果相比的误差均小于7%,所以采用式(1)作为蜂窝式压弯构件在弯矩作用平面内的整体稳定性的计算公式既满足精度要求又偏于安全。
5. 结论
1) 开孔率是影响蜂窝式压弯构件稳定承载力的重要因素,随开孔率的增加,蜂窝构件的极限稳定承载力下降。建议六边形孔蜂窝构件的开孔率在30%~40%之间,圆形孔蜂窝构件的开孔率在30%~50%之间。
2) 在开孔率与孔间距相同的条件下,圆形孔蜂窝构件的极限稳定承载力要稍高于正六边形孔蜂窝构件极限稳定承载力。两种孔型蜂窝构件的极限稳定承载力总体下降趋势基本一致。当孔间距增加时,蜂窝式压弯构件的极限稳定承载力提高。
3) 本文引入蜂窝构件换算长细比的概念,基于边缘屈服准则,提出了蜂窝式压弯构件在弯矩作用平面内的极限整体稳定性的计算公式,本文公式计算结果与有限元结果相比,误差均小于7%,计算结果既满足精度要求,又偏于安全。