基于MFO算法的含分布式电源配电网故障定位

Fault Location of Distribution Network with DG Based on MFO Algorithm

摘要: 针对分布式电源的接入，造成了故障电流的多向性，传统故障定位方法不再适用的问题。本文提出基于飞蛾扑火优化算法(MFO)的故障定位方法，采用馈线终端单元上传的电流状态信息作为判断依据。首先，将MFO算法中寻优主体的位置坐标进行二进制编码，使其与馈线终端单元上传的电流状态信息关联，将故障定位任务转化为二进制优化问题，其次将上报的过流告警与预期的过流状态进行判别，最后针对分布式电源的特点，构建新的开关函数，使其适用于分布式电源的动态投切，实现含分布式电源配电网的故障定位。通过对33节点配电网进行仿真实验，仿真结果表明该方法能够准确定位单一以及多重故障区段，在信息畸变情况下，仍能准确定位，具有良好的容错性，并且MFO算法与其他算法相比较收敛更快，全局寻优性更强。

Abstract: For the access of distributed power sources, the multi-directional fault overcurrent is caused, and the traditional fault location method is no longer applicable. In this paper, a fault location method based on the Moth-flame optimization algorithm (MFO) is proposed, and the current state infor-mation uploaded by the feeder terminal unit is used as the judgment basis. First, binary code the position coordinates of the optimization subject in the MFO to associate it with the current status information uploaded by the feeder terminal unit, and convert the fault location task into a binary optimization problem. The difference between the flow states is used as the objective function. Finally, according to the characteristics of the distributed power generation, a new switching function is constructed, which is suitable for the dynamic switching of the distributed power gen-eration, and realizes the fault location of the distribution network including the distributed power generation. Through the simulation experiment of the 33-node distribution network, the simulation results show that the method can accurately locate single and multiple fault sections, and it can still accurately locate in the case of information distortion, with good fault tolerance, and the MFO is comparable to other algorithms. The comparison converges faster and the global optimization is stronger.

1. 引言

配电网故障定位对于提高配电网供电可靠率，缩短停电时间，恢复配电网供电，起着至关重要的作用，故障区段定位是自愈智能配电网不可或缺的支持功能。其主要目的是定位故障路段并促进快速修复 [1] [2] 。然而，传统的故障定位模型大多建立在单源辐射配电网的基础上。对于典型放射状配电系统，分布式电源(distributed generation, DG)的接入改变了电网结构，DG的投切、馈线终端单元(feeder terminal unit, FTU)上传的电流状态信息丢失或畸变，都将对对配电网的故障定位造成影响 [3] [4] [5] 。

针对以上问题，文献 [6] 考虑DG接入配电网引起的故障电流的多向性，改进了开关功能，但不能应用于拓扑结构复杂的配电网。随着电网调度对DG动态投切，需要重新指定各个开关的正方向，故障定位过程效率较低。文献 [7] [8] 将DG的动态投切情况考虑在内，构建的开关函数中将DG的动态投切转换为电源接入系数之间的逻辑关系，使其适用于复杂配电网中DG的动态投切，但实际含DG的配电网故障情况复杂多变，存在无法对故障区段进行准确定位的情况，难以实现故障定位最优解，造成定位不准确的问题。文献 [9] 提出了一种线性模型，能适用于复杂的含DG配电网故障定位，但只适用于单故障情况，对于不可预测的配电网故障情况，难以适用。基于目前现状，本文构建了新的开关函数以及对现有评价函数进行了改进。同时，对于目前智能优化算法，如粒子群算法 [7] 、果蝇优化算法 [10] 、蝙蝠算法 [11] 、免疫算法 [12] 、遗传算法 [13] 等智能优化算法的仿生特点。提出采用以飞蛾扑火优化算法(Moth-Flame Optimization, MFO) [14] [15] [16] [17] 为基础的配电网故障定位方法，MFO算法由Seyedali Mirjalili教授在2015年提出，是一种仿生类智能优化算法，该算法结构简单，全局寻优能力强，收敛快速且不易陷入局部最优的优势。适用于解决数学模型约束条件下的寻优问题。

2. 飞蛾扑火优化算法

飞蛾扑火算法是根据飞蛾围绕火焰飞行的行为而提出的算法。在算法中，主要个体是飞蛾和火焰，它们都是优化问题的解集。飞蛾围绕火焰进行螺旋飞行，从而搜索最优解。由于MFO算法是属于生物仿生类算法，需要基于种群来求解问题，矩阵M表示飞蛾种群的位置，数组OM是飞蛾个体的适应度值，适应度值为算法求解的评价函数值。矩阵F与矩阵M类似，表示火焰的位置，数组OF与数组OM类似，表示火焰在当前位置的适应度值。

$M=\left(\begin{array}{ccc}{m}_{11}& \dots & m_{1d}\\ ⋮& \ddots & ⋮\\ m_{n1}& \cdots & m_{nd}\end{array}\right)$ $OM=\left(\begin{array}{c}O{M}_1\\ ⋮\\ O{M}_n\end{array}\right)$ (1)

其中n是飞蛾数量，d是变量个数即维数。

应该指出的是，飞蛾和火焰的不同之处，在于算法在每次迭代中采取了不同的处理更新方法。飞蛾是算法寻优的主体，它的位置作为寻优的解集，将计算所有飞蛾的适应度值进行排序后，更新最佳即飞蛾的位置是位置作为火焰的位置，可以用一个三元组表示，如式(2)所示：

$MFO=\left(I,P,T\right)$ (2)

I是生成飞蛾随机种群和适应度函数，如式(3)所示：

$I:\phi \to \left\{M,OM\right\}$ (3)

P函数是飞蛾移动的主函数，矩阵M通过P函数更新，并作为新的矩阵M，如式(4)所示：

$P:M\to M$ (4)

$T:M\to \left\{true,false\right\}$ (5)

式(5)表示P函数更新矩阵M直到满足最大迭代次数。即T函数返回true，否则M矩阵将继续迭代更新。

$M_i=S\left(M_i,F_j\right)$ (6)

$S\left(M_i,F_j\right)=D_i\cdot \exp \left(bt\right)\cdot \cos \left(2\pi t\right)+F_j$ (7)

$D_i=\left|F_j-M_i\right|$ (8)

数学模型(6)模拟了算法仿生中飞蛾扑火的生物行为，其中M_i，F_j分别表示第i个飞蛾和第j个火焰；该算法的飞蛾种群会被分成几个子种群，围绕自己所属的火焰进行运动，为防止算法陷入局部最优，本文采用式(7) S函数(对数螺旋函数)更新飞蛾与火焰之间的相对位置，同时根据飞蛾适应度值的排序，将最优的位置更新为火焰的位置；D_i表示第j各火焰与第i个飞蛾的距离，如式(8)所示；b为常数，定义螺旋的形状；t为[−1, 1]区间内的随机数，定义了飞蛾种群中的下一代与火焰的位置相距程度，t = −1时最近，t = 1时最远。

其中飞蛾和火焰分别作为该对数螺旋线的起点和终点，飞蛾可以在螺旋线范围内绕着火焰飞行。因此，可以保证寻优空间的探索和开发。但在寻优空间中，由于飞蛾是相对于不同的火焰进行飞行，不同的火焰其适应度值存在优劣，为了提高飞蛾对较优位置火焰的利用。所以采用式(9)解决该问题。

$flameno=round\left(N-l\ast \frac{N-1}{T}\right)$ (9)

式(9)中为l为当前迭代次数，N是火焰种群初始量，T为最大迭代次数。

算法具体步骤可表示为：

1) 初始化飞蛾和火焰种群，初始时飞蛾种群数与火焰种群数相等；由飞蛾和火焰的位置通过评价函数计算出适应度值；

2) 将步骤2)中的适应度值进行优劣排序，将当前序列中最优适应度值对应的位置作为火焰下一代的位置；

3)飞蛾通过式(7)对自己的位置进行更新，并计算出该位置所对应的适应度值，加入序列中进行重新排序，更新最优解以及火焰数量；

4) 判定终止条件是否满足，如果满足，则输出最优解以及位置，如果不满足，则返回步骤3)。

3. 含分布式电源配电网故障定位原理

3.1. 构建评价函数

在传统的单电源配电网中，当配网线路发生故障时，潮流方向是单一的，故障电流都是从系统电源侧流向故障点。所以评价函数为：

$F_{it}\left(x\right)=\left|I_1-I_1^{\ast }\left(x\right)\right|+\cdots +\left|I_j-I_j^{\ast }\left(x\right)\right|+\cdots +\left|I_N-I_N^{\ast }\left(x\right)\right|+w\left(\left|x_1\right|+\cdots +\left|x_i\right|+\cdots +\left|x_M\right|\right)$ (10)

式中x_i表示配电网中第i个馈线区段的状态，故障为1，正常为0；I_j表示第j号开关处的FTU上传的实际电流状态信息，该信息会因为环境或设备等原因产生畸变或丢失，其取值分为1和0两种情况，分别表示第j号测控点检测到故障电流和没检测到故障电流； $I_j^{\ast }\left(x_i\right)$ 表示配电网中各测控点的预期状态，测控点的预期状态是描述设备状态的函数即开关函数；其中 $\left|I_N-I_N^{\ast }\left(x\right)\right|$ 为判别项； $w\left(\left|x_1\right|+\cdots +\left|x_M\right|\right)$ 为误判项，w为误判系数，取值为[1, 0]范围内的实数。评价函数的原理是求得测控点的实际状况和开关函数求得的设备状态之间的偏差最小即所求评价函数的最小值，表明故障定位越准确。防误判项的具体原理可参考文献 [7] [8] 。

在含DG的配电网中，当线路发生故障时，故障电流是从系统电源和DG流向故障点。传统的单电源故障定位评价函数不再适用。现需要对第j号开关处的编码方式进行重新定义，规定系统电源指向DG或用电侧的方向为配电网唯一的正方向，具体如下：

$I_j=\{\begin{array}{l}1\left(检测到正方向的故障电流\right)\\ -1\left(检测到负方向的故障电流\right)\\ 0\left(未检测到故障电流\right)\end{array}$ (11)

3.2. 构建开关函数

开关函数表示了故障区段和开关状态的逻辑关系，由式(10)可知故障定位关键在于求得测控点的实际状况和开关函数求得的设备状态之间的偏差最小的解集合。所以开关函数的构建的关键是当FTU上传的状态信息无畸变时，I_j应该于 $I_j^{\ast }$ 状态信息保持一致。所以，本文构建新的开关函数式(12)。

$\begin{array}{l}\{\begin{array}{l}{I}_{ju}^{*}=\left\{{\displaystyle \underset{u}{\overset{M^{\ast }}{\sum }}\left[K_u\left(1-{\displaystyle \underset{i_1}{\sum }{x}_{j,s_u}\left(i_1\right)}\right)\right]}\right\}{\displaystyle \underset{j,d}{\overset{N}{\sum }}{x}_{j,d}}\\ I_{jd}^{*}=\{\begin{array}{l}0\text{if}{K}_d=0\\ \left\{{\displaystyle \underset{d}{\overset{N^{*}}{\prod }}\left[{}^{\neg }{K}_d\parallel \left(1-{\displaystyle \underset{i_2}{\sum }{x}_{j,s_d}}\left(i_2\right)\right)\right]}\right\}{\displaystyle \underset{j,u}{\overset{M}{\sum }}{x}_{j,u}}\text{else}\end{array}\end{array}\\ I_j^{*}=I_{ju}^{*}-I_{jd}^{*}\end{array}$ (12)

式中“∑”、“||”表示“逻辑或”运算；“∏”表示“逻辑与”运算，“ ${}^{\neg }$ ”表示“逻辑非”运算。式(13)中，以第j号开关为界，将配电网拓扑结构分为上游和下游，其中含系统主电源的区域为上游，其余区域为下游。K_u、K_d分别表示第j号开关上游、下游的电源开关系数，电源接入为1，断开为0，含系统主电源的区域开关系数始终为1，其中值得注意的是当j号开关下游的电源开关系数K_d全为0时， $I_{jd}^{*}=0$ ；M^*、N^*分别表示配电网第j号开关上、下游电源数量； $x_{j,s_u}$ 、 $x_{j,s_d}$ 分别表示从第j号开关到上、下游含电源支路所经过的馈线区段状态信息，当馈线区段出现故障时为1，否则为0；x_j,u、x_j,d分别表示第j号开关上、下游所有馈线区段的状态信息，当馈线区段出现故障时为1，否则为0；M、N分别表第j号开关上、下游所有馈线区段的数量。

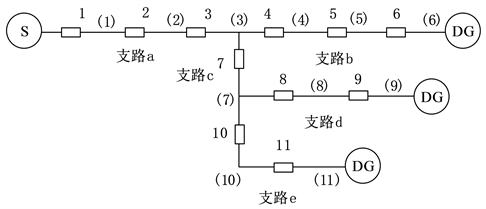
Figure 1. Power grid topology with distributed generation

图1. 含分布式电源电网拓扑图

以图1为例，第5号开关的下游为区段5和区段6，其余区域为上游。当区段5和区段8发生故障时，FTU上传故障电流序列信息为I = [1 1 1 1 1 −1 1 1 −1 −1 −1]，利用式(12)计算各测控点的预期状态，如下所示：

$\begin{array}{l}\{\begin{array}{l}{I}_{1u}^{*}=\left(1-0\right)\times \left(x_1\parallel x_2\parallel x_3\parallel \cdots \parallel x_{10}\parallel x_{11}\right)=1\\ I_{1d}^{*}=\{\left[0\parallel \left(1-x_1\parallel x_2\parallel x_3\parallel x_4\parallel x_5\parallel x_6\right)\right]\times \left[\text{0}\parallel \left(1-x_1\parallel x_2\parallel x_3\parallel x_7\parallel x_8\parallel x_9\right)\right]\\ \times \left[0\parallel \left(1-x_1\parallel x_2\parallel x_3\parallel x_7\parallel x_{10}\parallel x_{11}\right)\right]\}\times 0=0\end{array}\\ I_1^{*}=I_{1u}^{*}-I_{1d}^{*}=1\end{array}$ (13)

同理可得 $I_2^{*}=I_3^{*}=I_4^{*}=I_5^{*}=1$ ， $I_6^{*}=-1$ ， $I_8^{*}=1$ ， $I_9^{*}=I_{10}^{*}=I_{11}^{*}=-1$ ，特别指出由式(12)计算得 $I_7^{*}=1$ ，与FTU上传故障电流状态信息保持一致。具体计算步骤如式(14)所示：

$\begin{array}{l}\{\begin{array}{l}{I}_{7u}^{*}=\left[\left(1-x_1\parallel x_2\parallel x_3\right)\parallel \left(1-x_3\parallel x_4\parallel x_5\parallel x_6\right)\right]\times \left(x_7\parallel x_8\parallel x_9\parallel x_{10}\parallel x_{11}\right)=1\\ I_{7d}^{*}=\left\{\left[\text{0}\parallel \left(1-x_7\parallel x_8\parallel x_9\right)\right]\&\&\left[0\parallel \left(1-x_7\parallel x_{10}\parallel x_{11}\right)\right]\right\}\times \left(x_1\parallel x_2\parallel x_3\parallel x_4\parallel x_5\parallel x_6\right)=0\end{array}\\ I_7^{*}=I_{7u}^{*}-I_{7d}^{*}=1\end{array}$ (14)

式中“&&”表示“逻辑与”运算。

3.3. 改进评价函数

由式(11)所示，含DG的配电网中I_j存在三种可能性，即“−1、0、1”。当FTU上传的电流状态信息发生畸变时，I_j与 $I_j^{\ast }$ 的差值最大可能为2，即某处电流状态信息由−1畸变为1，或由1畸变为−1。整体来看会导致评价函数的误判项在整个评价函数中所占的权重变小。导致故障诊断“最小集”概念中“可能的故障诊断结果中选择最小数量的故障设备”这一原则失效，导致定位的误判。针对上述问题对式(10)进行改进，如式(15)

$F_{it}\left(x\right)=\left|{}^{\neg }\left[I_1==I_1^{\ast }\left(x\right)\right]\right|+\cdots +\left|{}^{\neg }\left[I_j==I_j^{\ast }\left(x\right)\right]\right|+\cdots +\left|{}^{\neg }\left[I_N==I_N^{\ast }\left(x\right)\right]\right|+w\left(\left|x_1\right|+\cdots +\left|x_i\right|+\cdots +\left|x_M\right|\right)$ (15)

式中“ ${}^{\neg }$ ”表示“逻辑非”运算，“==”表示条件运算符中的“等于运算符”，其中w含义式(10)一致。

“ $\left|{}^{\neg }\left[I_j==I_j^{\ast }\left(x\right)\right]\right|$ ”表示当I_j与 $I_j^{\ast }$ 相等时输出“0”，否则输出“1”，仅判断信息编码是否相等，当电

流状态信息畸变时，降低原评价函数各判别项可能导致的差值过大，提高误判项在评价函数中所占权重，提高容错率，本文中w取值0.5。

3.4. 上传状态信息产生畸变

在实际配电网故障定位过程中随着配电网的日益复杂，FTU上传的故障状态信息也在扩大，也会存在一定的状态信息畸变概率和状态信息丢失的情况。在处理信息畸变或丢失的情况中，一部分错误信息可以通过故障电流流向的连续性和逻辑性进行识别。以图1为例，当区段5和区段8发生故障时，FTU上传故障电流序列信息为I = [1 1 1 1 1 −1 1 1 −1 −1 −1]，当I₂发生畸变为“−1”时，表示测控点2由负方向的故障电流流过，而测控点2相邻上、下游测控点电流状态信息为1，表示测控点1和测控点3都有正方向的故障电流流过，从其故障电流流动的连续性和逻辑来判定出I₂发生畸变。但也存在比较特殊的畸变情况，仍以当区段5和区段8发生故障为例，如当I₅发生畸变为“−1”时，此时电流序列信息为I = [1 1 1 1 −1 −1 1 1 −1 −1 −1]，与区段4和区段8故障时电流序列信息一致，导致畸变信息无法被判断。当电流状态信息序列与实际某区段故障时电流状态信息序列一致，这种畸变无法通过连续性和逻辑性判别。

现将畸变分为两种情况：

1) 可识别畸变：畸变后的故障电流方向与该节点前后电流方向存在电流流向和逻辑的错误。

2) 不可识别畸变：畸变后的故障电流方向，与某种实际故障区段故障电流方向一致，无电流流向和逻辑的错误。

以下讨论均在情况(1)的前提下进行。

3.5. 飞蛾扑火优化算法二进制编码改进及故障区段定位应用流程

本文配电网区段状态值只有0或1两种情况，即故障区段定位本质上是个“0-1”离散变量优化问题。基本MFO算法不能直接用于求解该配电网故障区段定位问题，所以，在实际应用时，需要将飞蛾和火焰种群位置进行二进制编码。本文将对种群位置m_nd采用sigmoid函数 [18] 进行二进制编码，具体方式为如下：

$h\left(m_{nd}\right)=\frac{1}{1+e^{-m_{nd}}}$ (16)

转换原则为：

$x_i=\{\begin{array}{l}1\text{if}h\left(m_{nd}\right)>rand\left(1,0\right)\\ 0\text{else}\end{array}$ (17)

基于FTU上传的故障电流状态信息，利用二进制MFO算法故障区段定位求解流程，就是将d维空间内的飞蛾种群进行优化求解，所求的飞蛾位置即为故障的区段，位置序列代表区段序列，将该位置和火焰位置以及故障电流状态信息代入开关函数和评价函数中进行计算，通过算法的每次迭代计算，输出达到数学模型约束条件的最优位置序列，该最优位置序列即为最逼近配电网区段实际状态。具体流程如图2所示。

Figure 2. Algorithm flow chart

图2. 算法流程图

4. 算例仿真验证

为验证本文所提算法和模型的效果及有效性，采用图3所示的含DG的33节点配电网结构拓扑进行仿真算例分析。

Figure 3. The 33-node distribution network structure topology with DG

图3. 含DG的33节点配电网结构拓扑图

图3中S和DG1、DG2、DG3表示分别表示系统主电源和分布式电源，且Ki代表DG接入配电网的开关系数，接入为1，断开为0。编号为1~33的矩形框表示断路器以及分段开关；编号为(1)~(33)表示各相邻矩形方框之间表示馈线区段。规定该配电网正方形方向如图3中所示。本次仿真实验通过Matlab R2018a进行。

Table 1. Fault type

表1. 故障类型

Table 2. Simulation results of model examples

表2. 算例仿真结果

由表1和表2可知，在实验中，本文构建的数学模型在DG投切变化的情况下定位结果全部正确，并且在电流状态信息多重畸变的情况下，仍能准确定位故障区段，适用于情况复杂多变的含DG配电网故障定位。通过对比表1中FTU上传的故障电流状态序列和表2中开关函数，两者保持一致，表明本文构建的开关函数符合本文当FTU上传的状态信息无畸变时，I_j应该于 $I_j^{*}$ 状态信息保持一致的思想。

此外本文还分别在区段6、13、29设置故障，将节点17电流状态信息由−1畸变为0，节点28电流状态信息由0畸变为1的预设条件下，即电流状态信息序列I = [1 1 1 1 1 1 0 −1 −1 0 0 1 1 −1 −1 −1 −1 −1 1 1 1 1 0 0 0 0 0 0 0 −1 −1 −1 −1]畸变为I = [1 1 1 1 1 1 0 −1 −1 0 0 1 1 −1 −1 −1 1 −1 1 1 1 1 0 0 0 0 0 −1 0 −1 −1 −1 −1]，对飞蛾扑火优化算法(MFO)、鲸鱼优化算法(WOA)、人工蚁群算法(ABC)和萤火虫算法(FA)进行仿真对比，实验共进行30次，种初始群和迭代次数分别设置为30和100。随机抽取一次作为算法仿真对比结果如图4所示。

由图4可知MFO算法收敛速度方面弱于WOA算法，但具有良好的全局收敛性，WOA算法则更容易陷入局部最优，快速收敛但并没有找到最优解。MFO与ABC算法以及FA算法相比，分别在第27代、86代、65代达到相同适应度值3.5，MFO算法具有更快的收敛速度和寻优效果。

对30次算法比较实验进行统计，4种算法性能对比结果如表2所示。

由表3可知，在三重故障区段，两节点信号畸变的情况下，4种算法中WOA算法平均迭代时间最短，但定位准确率偏低，而MFO算法相对于WOA、ABC、FA算法定位准确率提高了53%、17%和13%，说明MFO算法既保证了收敛速度的同时，也保证了定位的精确度，验证了MFO算法的优越性。

Figure 4. Comparison of algorithm simulation

图4. 算法仿真对比

Table 3. Comparison of algorithms performance

表3. 算法性能比较

5. 结论

1) 本文通过对多重故障，多重电流状态信息畸变场景的预设进行算法仿真实验，验证了飞蛾扑火优化算法在含分布式电源的配电网故障定位的有效性以及容错性。

2) 本文受到现有故障定位数学模型的启发，构建了适用于含分布式电源配电网的故障定位开关函数，以及对传统评价函数的改进。使新开关函数计算出来的测控点状态与FTU上传的实际测控点状态差值最小，使之更加逼近实际状态。通过仿真验证了模型的性能，并且适合于具有多故障和信息畸变的含分布电源的复杂配电网，具有较高的容错能力。

3) 通过MFO算法与WOA、ABC、FA算法在多故障，多电流状态信息畸变情况的分析对比，发现MFO算法具有很强的搜索性能和快速的收敛性。与其他的智能优化方法相比，该算法在结构上更简洁、所需的参数少、求解精度高、所需迭代次数少等优点。

4) 本文以可识别的畸变情况作为前提假设，对故障定位进行模拟，对于畸变电流信息无法识别的故障定位还需进行进一步的研究，同时，飞蛾扑火优化作为仿生类智能优化算法，仅采用自身仿生特性，还有进一步的改进空间。