基于卷积神经网络的人脸表情识别算法

Facial Expression Recognition Algorithm Based on Convolutional Neural Network

摘要: 人脸表情识别是图像识别的一个重要领域。传统人脸表情识别主要基于人工提取特征，由于人脸表情丰富、背景复杂、差异范围大等问题，其存在算法鲁棒性较差、易受人脸身份信息干扰等问题，以及传统卷积神经网络易发生过拟合、梯度弥散、梯度爆炸等问题的现状，因此本文提出一种多层特征融合非反向传播稠密卷积神经网络的人脸表情识别算法。该算法应用了改进的HSIC (Hilbert-Schmidt Independence Criterion，希尔伯特–施密特独立性)-bottleneck来代替传统反向传播(Back Propagation, BP)，具有诸多独特的优点。在特征提取过程中，为了充分利用得到的特征图像，将卷积层稠密连接并引入attention机制，最终通过softmax分类器分类，得到分类结果。在FER2013数据集上进行了多次实验，与传统BP算法的卷积神经网络算法相比，不仅有效减轻过拟合现象，并且在模型收敛速度上更快、计算量更小、内存占用更小，证明了在人脸表情识别问题中非反向传播稠密卷积神经网络模型结构有效、提出的分类优化方法可行。

Abstract: Facial expression recognition is an important field of image recognition. Traditional facial expression recognition is mainly based on manual extraction of features, which has the problems of poor algorithm robustness and susceptibility to interference by face identity information due to rich facial expressions, complex background and large range of differences, as well as the current situation that traditional convolutional neural networks are prone to overfitting, gradient dispersion and gradient explosion, etc. Therefore, this paper proposes a multilayer feature fusion using dense convolutional neural network without Back Propagation (BP) for face expression recognition algorithm. The algorithm applies a modified HSIC (Hilbert-Schmidt independence criterion)-bottleneck instead of the traditional BP, which has many unique advantages. In the feature extraction process, in order to make full use of the obtained feature images, the convolutional layers are densely connected and attention mechanism is introduced, and finally the classification results are obtained by the softmax classifier. Compared with the traditional BP algorithm of convolutional neural network algorithm, it not only effectively reduces the overfitting phenomenon, but also has faster model convergence, smaller computation and smaller memory consumption, which proves that the structure of non-back propagation dense convolutional neural network model is effective and the proposed classification optimization method is feasible in the face expression recognition problem.

1. 引言

在计算机视觉领域中，图像识别技术日益成熟，人脸表情识别成为了热点研究课题。人脸识别问题相较其他问题而言，不仅需要考虑拍摄光照、遮挡和角度问题，同时还需要考虑人脸身份特征及人脸表情非刚性变化的特征。美国著名心理学家Mehrabian提出 [1] ，在人类的日常交流中，通过语言、声音传递的信息分别占全部的信息总量的7%和38%，而通过人脸表情传递的信息量则占到了55%。美国心理学家Ekman和Friesen通过大量实验 [2] ，定义了人类六种基本表情：高兴、生气、惊讶、害怕、厌恶和悲伤。2013年，Shaohua Wan等人使用Gabor变换来提取特征 [3] ，降低了人脸姿态变化对识别准确率的影响。2015年，Ali等人利用经验模态分解(Empirical Mode Decomposition, EMD)技术 [4] 进行人脸表情识别，将二维图像经过连续投影得到面部特征图，并使用EMD技术对面部特征图进行分解。Liu等人将Riesz基量局部二元模式和直推式传输线性判别分析相结合 [5] ，针对野外环境进行人脸表情识别，实现了较高的识别准确率。另外，Shin等人使用独立分量分析和主成分分析在情感维度上进行表情识别 [6] 。Lajevardi等人将三维彩色图像展开为二维矩阵 [7] ，使用Lob-Gabor滤波器提取特征，并且使用线性判别分析分类器对特征进行分类。传统人脸表情识别过程中的特征提取很大程度上依靠人为干预，算法鲁棒性差且精度不高。

现阶段，深度学习作为机器学习研究的一个新的领域，受到人们的广泛关注。深度学习在时效性和准确性上有了显著的提高。深度学习为越来越广泛的图像分类识别任务带来了新的性能水平，但目前深度学习算法的误差反向传播过程通常在生物学上被认为是不合理的 [8] [9] [10] ，不符合人脑神经网络的信号传播过程，同时随机梯度下降算法(Stochastic Gradient Descent, SGD)等相关梯度下降算法既耗费时间、占用大量内存，且伴随需要不断搜索合适的诸多超参数和梯度弥散、梯度爆炸的问题。2019年，Wan-Duo Kurt Ma等人采用统计特征与输入和标签之间的相关独立性的方法 [11] ，代替传统的反向传播训练，但该方法在复杂的卷积神经网络以及特征重用网络中的结果与反向传播(Backward Propagation, BP)算法的结果还有一定差距。因此，本文提出了改进的HSIC-Bottleneck方法在理论和实际上替代神经网络的梯度反向传播算法，同时为了更好地利用提取到的图像特征，借鉴FPN (Feature Pyramid Networks)，采用多个稠密卷积模块，在每个模块中将不同尺度的特征图在channel维度上进行拼接，并赋予每层特征在拼接时的权重，在前向传播过程中采用稠密连接的卷积层，且每层的输入由前面所有层的输出拼接而成，最大程度的利用提取到的特征。

在本文中，通过最大化隐藏层的输出与标签之间的互信息(Mutual Information)，且最小化隐藏层与输入之间的相互依赖，来确定损失函数的表示，这样就可以用最少的输入特征来预测输出，去掉冗余的特征，使得隐层特征高度效率化，增加了模型抑制过拟合的能力，提高了模型的泛化性，从原理和实际上改进了神经网络的训练方法，与2019年Wan-Duo Kurt Ma等人提出的HSIC-Bottleneck算法 [12] 相比，本文提出的算法使用trace法代替行列式法得到目标函数，且在特征之间加入特征重用，并引入注意力机制，这样可以将较大的感受野与较小的感受野相结合，使得特征的提取更加高效，对较大目标和小物体的检测效果都更加精准。本文试验使用FER 2013数据集进行测试，与传统反向梯度传播算法相比，在准确率明显提升的同时收敛速度明显提高，且泛化能力加强，计算量和内存占用大幅减少。

2. 非反向传播的卷积神经网络

目前国内外的卷积神经网络主要优化方法是SGD等相关的梯度下降算法 [13] ，使用从全局各个分类的误差获得的负梯度最大的方向，将全局寻优任务分解为一个小的子问题的集合，来逐层更新权重和偏置参数，这样使其具有了在较大的模型结构中训练参数多、所需算力较高、计算量庞大等缺点。反向梯度传播算法在生物学中的合理性一直以来都是一个备受争议的话题，也是探索替代方案的一个动机。在反向梯度传播算法中一个明显不符合生物学的问题是突触权重根据后面层的误差调整，这在生物学的理论中是不合理的 [14] [15] 。另一个问题是在前向传播和反向传播过程中，权重矩阵是共享的 [16] [17] ，此外反向传播是线性计算的且在计算前向传播时必须停止反向传播，反之亦然 [18] 。因此，寻找更加合理的反向传播替代方案已经成为DNN (Deep Neural Network)领域急需解决的重要问题，也是迫在眉睫的要求。

2019年，Wan-Duo Kurt Ma等人提出的一种代替反向传播的方法 [11] ，引用了HSIC度量，使用抽样来测量两个分布依赖的强弱。该方法避免了梯度弥散、梯度爆炸现象的发生，可以在某层没有梯度的情况下跨层优化，可以同时并行优化多个层，但是在复杂的卷积神经网络中对于小物体检测的效果和传统反向传播训练算法相比还有一定差距。因此，本文提出一种改进的HSIC-Bottleneck方法来代替传统反向传播训练，基于希尔伯特空间核方法，将原始数据映射为再生核希尔伯特空间(Reproducing Kernel Hilbert Space, RKHS)中的核函数，然后再构造协方差算子来描述条件独立性，根据条件独立性的定理可以得到度量独立性和条件独立性的目标函数。在实际操作中，根据样本数据来构造经验条件协方差算子，通过RKHS中的内积运算可得到以Gram矩阵表示的估计函数。

信息论(Information Theory) [19] 是学习理论和大量研究的基础。信息瓶颈(Information Bottleneck, IB)原则 [20] 概括了最小充分统计的概念，表示了最优化的平衡预测输出所需的信息与保留的关于输入的信息之间的关系，最优解可由下式得到：

$\underset{p_{O_i|X},p_{Y|O_i}}{\min }I\left(X;O_i\right)-\beta I{\left(O_i;Y\right)}_i$

其中X、Y分别表示输入和标签， $O_i$ 表示在第i个隐藏层的输出， $\beta$ 表示拉格朗日乘数， $I\left(X;O_i\right)$ 与 $I\left(O_i;Y\right)$ 分别表示X与 $O_i$ 之间以及 $O_i$ 与Y之间的互信息。从公式可看出，IB主要保留了在压缩输入数据的特征信息时，隐藏层中关于标签的输出信息，即在保留预测所需的重要信息的同时去除无关的信息，达到平衡和消除冗余信息的目的。

实际中，由于很多原因导致IB难以计算。如果输入信号是连续的(如语音信号)，除非向网络中添加噪声信号，否则互信息 $I\left(X;O_i\right)$ 是无限的，因此许多算法将输入数据进行分箱操作，这样不会将数据扩展到高维，但这样会由于分箱的规则不同导致得到的结果也不同。额外的影响因素如离散和连续数据之间以及离散数据和差分熵之间的不同。本文使用HSIC代替在IB目标中的互信息，与互信息估计不同的是HSIC采用关于时间复杂度 $\text{O}\left(l^2\right)$ 的鲁棒计算方法，其中l代表输入数据的数量。

HSIC是RKHS [12] 的数据分布之间的交叉协方差算子的Hilbert-Schmidt范数，如下式所示：

$\begin{array}{c}\text{HSIC}\left(P_{MN},H,G\right)={\Vert C_{mn}\Vert }^2\\ =E_{MN{M}^{\prime }{N}^{\prime }}\left[k_m\left(m,m^{\prime }\right)k_y\left(y,y^{\prime }\right)\right]+E_{M{M}^{\prime }}\left[k_m\left(m,m^{\prime }\right)\right]E_{N{N}^{\prime }}\left[k_n\left(n,n^{\prime }\right)\right]\\ -2E_{MN}\left\{E_{M^{\prime }}\left[k_x\left(m,m^{\prime }\right)\right]E_{N^{\prime }}\left[k_n\left(n,n^{\prime }\right)\right]\right\}\end{array}$

其中 $m\in M,n\in N$ 为输入数据，N为样本标签， $k_m,k_n$ 代表核函数， $H,G$ 表示希尔伯特空间， $E_{MN}$ 表示MN的期望，由上式可推出以下表达式：

$\text{HSIC}\left(P_{MN},H,G\right)={\left(l-1\right)}^{-1}tr\left(K_{M}H{K}_{N}H\right)$

其中，l代表样本数量， $K_M\in R^{l\times l},K_N\in R^{l\times l},K_{M_{ij}}=k\left(m_i,m_j\right),K_{N_{ij}}=k\left(n_i,n_j\right),H\in R^{l\times l}$ 是一个中心对称的和幂等矩阵，tr表示矩阵的迹，这样一来计算代价只与样本的数量有关，尤其适合计算高维的小样本数据。

在一个由h个隐藏层构成的全连接网络中，隐藏层的输出矩阵维度为 $\left(1,d_i\right)$ ，其中 $i\in \left\{1,\cdots ,h\right\}$ ， $d_i$ 表示第i个隐藏层单元数量，则每个batch-size的隐藏层输出矩阵大小为 $\left(b,d_i\right)$ ，其中b为batch-size大小，在应用IB原则计算目标函数过程中，使用HSIC代替互信息可得：

$Z_i^{\ast }=\underset{Z_i}{\arg \min }\text{HSIC}\left(Z_i,X\right)-\beta \text{HSIC}\left(Z_i,Y\right)$

其中X为输入数据，Y为标签数据， $\beta$ 是表示拉格朗日乘数，则HSIC的各项可如下表示：

$\text{HSIC}\left(Z_i,X\right)={\left(l-1\right)}^{-1}tr\left(K_{Z_i}H{K}_{X}H\right)$

$\text{HSIC}\left(Z_i,Y\right)={\left(l-1\right)}^{-1}tr\left(K_{Z_i}H{K}_{Y}H\right)$

上式表明了最佳的隐藏层输出 $Z_i$ 在不依赖于输入的冗余信息和与输出具有最大相关性之间找到了平衡。理想情况下当 $Z_i^{\ast }$ 收敛时，预测标签所需的信息会被保留，且消除了导致过拟合的冗余信息。

3. 改进的稠密卷积神经网络

在传统CNN前馈网络中，浅层提取的特征较为粗略，检测到的是类似边缘的一些特征，将浅层特征可视化结果如图1所示。

在中间部分的卷积层提取到的特征就较为抽象，可以检测到部分的物体，例如面部器官或比较高级的纹理特征，将提取到的特征可视化结果如图2所示。

而在最后部分的卷积层提取到的特征就更加抽象，可能检测到完整的物体，例如人脸或更加高级的纹理特征，将提取到的特征可视化结果如图3所示。

Figure 1. Visualization of shallow features

图1. 浅层特征可视化效果图

Figure 2. Visualization of middle layer features

图2. 中间层特征可视化效果图

Figure 3. Visualization of the final layer features

图3. 最后层特征可视化效果图

本文采用稠密连接的卷积神经网络，将相同尺度的特征图在channel维度进行拼接。使用多个稠密卷积模块相连，在每个稠密连接模块中有5层卷积，在拼接时分配给每层的输出特征不同的权重项。在前向传播过程中，稠密连接模块中的每一层都与其它所有层相连，即每一层都将之前所有层输出的图像特征连接起来作为自己的输入，并将自己的输出传递给之后的所有层，增强了图像特征在各个层之间的流动，充分利用了提取到的图像特征，稠密连接模块的结构如图4所示。

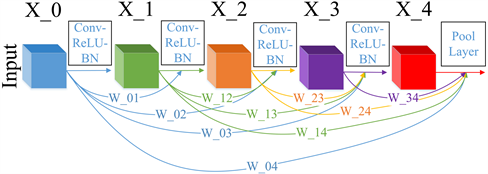
Figure 4. Diagram of the structure of the dense connection block

图4. 稠密连接模块结构示意图

由于浅层卷积层得到的特征图较大，感受野较小，对小物体的检测比较敏感，但对物体的整体特征表达不够完整，而较深的卷积层特征图尺寸较小，感受野较大，可以很好的表达物体的整体特征，但细节特征表达有所缺失。因此，本文采用FPN将不同尺寸的特征图进行融合，对语义强但分辨率低的高层次特征进行上采样，并与高分辨率特征相结合，生成高分辨率和语义强的特征表示，充分的利用提取到的特征，并引入attention机制，在拼接时赋予之前层一定的权重值，这样每层的输入均为前面所有层的输出，加强了对小物体检测的敏感度同时还不丢失整体特征的表达。将前馈网络结构进行可视化展示，结果如图5所示。

Figure 5. Diagram of the structure of the feed-forward network

图5. 前馈网络结构图

由图5可知，网络共包含3个block，其中block表示稠密连接模块，三个稠密连接模块的输出通过FPN进行融合，然后经过全局平均池化降维成二维向量。layer_11为注意力机制模块，经过全连接层后可计算出每个通道维度的注意力得分，以达到对重要信息更加关注的效果，同时可去除冗余信息。其中，预训练网络为除layer_11外的隐藏层。

4. 人脸表情分类实验

本文所做的实验是基于Python语言的Tensorflow框架，采用Tensorboard将结果进行可视化，硬件平台CPU采用Intel Core i7-9700k，GPU采用单块NVIDIA GeForce RTX 2080，显存为8 GB。

4.1. 数据集预处理

本文采用2013年Kaggle比赛用的FER2013公开数据集，数据集以csv文件的形式保存，数据信息包含表情分类的标签、像素值、用途(训练、验证、测试)，数据样本示例如图6所示。

Figure 6. Example of data sample

图6. 数据样本示例

将数据按用途分为训练集、开发集和测试集三部分，其中训练集数据28708条，开发集和测试集各3589条，训练集、开发集、测试集数据样本示例如图7所示。

Figure 7. Example of training set, validation set and test set data samples

图7. 训练集、验证集、测试集数据样本示例

训练集、开发集、测试集数据标签的分布直方图如图8所示。

将数据中的像素值还原为图像，可得到48 × 48的灰度图，共有7种表情：愤怒、厌恶、恐惧、高兴、悲伤、惊讶、中性，对应图像示例如图9所示。

4.2. 实验结果分析

在本文实验中比较了在使用相同参数情况下的传统反向传播训练的网络与非反向传播的网络的性能，传统网络使用交叉熵损失函数和Adam优化器，并且测试了采用不同数量稠密卷积模块的非反向传播网络的性能，并比较了在使用不同激活函数时的性能，测试了在不同的学习率下的收敛速度及最终分类结果，最后比较了在使用相同参数的情况下，本文提出的算法与目前最先进的三种算法的结果，验证了算法的性能 [21] 。在训练时，HSIC-Bottleneck的拉格朗日乘数β根据经验设置为100。

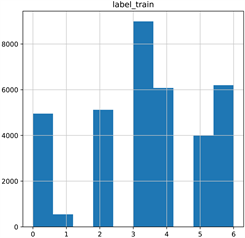
Figure 8. Histogram of label distribution for training set, validation set, and test set data

图8. 训练集、验证集、测试集数据标签分布直方图

Figure 9. Example of 7 expressions in FER2013 expression library

图9. FER2013表情库7种表情示例

为了验证本文提出的非反向传播算法，使用深造训练的网络和传统反向传播训练的网络准确率和损失值变化如图10和图11所示。

在图10、图11中，横坐标表示训练步数，共训练10,000步，纵坐标分别表示准确率和损失值，最终准确率达到了0.9946。从图10、图11中可以看出，传统BP算法在10,000时还未达到收敛，而非反向传播算法在2500步时达到收敛，非反向传播的网络具有更高的准确率，且收敛速度更快，这是因为本文提出的模型可以去除冗余的特征信息，且使得每层的特征与输出的相关性更强，在减少计算量的同时加快了模型收敛速度。在传统的反向传播训练中，计算复杂度很高，基于后面的梯度顺序向前计算所有层，往往需要高级的算力。相比之下，提出的HSIC-Bottleneck可以单独训练每一层，允许每层单独优化，并不向前传递梯度，实现并行计算，更好的提高了计算效率。在使用不同数量的稠密卷积模块测试时的准确率变化如图12所示。

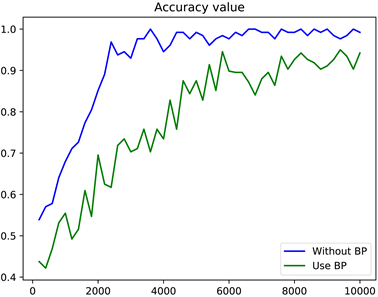
Figure 10. Accuracy curves of non-back propagation networks and BP networks with the same structure and parameters

图10. 具有相同结构及参数的非反向传播网络与BP网络准确率变化曲线

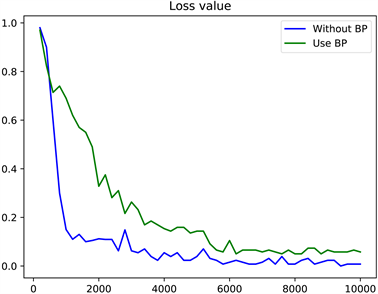
Figure 11. Curves of loss values of non-back propagation networks and BP networks with the same structure and parameters

图11. 具有相同结构及参数的非反向传播网络与BP网络损失值变化曲线

Figure 12. Accuracy curves of different number of dense convolution blocks

图12. 不同数量稠密卷积模块准确率变化曲线

在图12中横坐标代表训练步数，共训练10,000步，纵坐标代表准确率。从图中可以看出，在使用3个稠密卷积模块时效果最好，在准确率更高的同时收敛速度更快，在使用4个稠密卷积模块时会使参数量增加，导致模型的收敛速度降低。在使用不同的激活函数测试时的结果如图13所示。

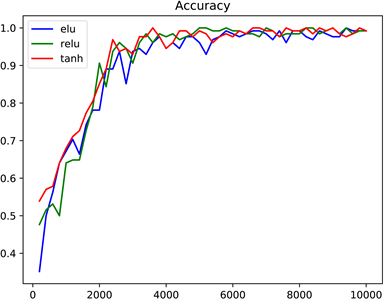
Figure 13. Accuracy curves when using different activation functions

图13. 使用不同激活函数时准确率变化曲线

从图13中可以看出，使用tanh函数和elu函数得到的结果几乎一样，但不如relu函数表现好。非反向传播算法在使用不同的学习率时，模型在训练过程中的表现如图14所示。

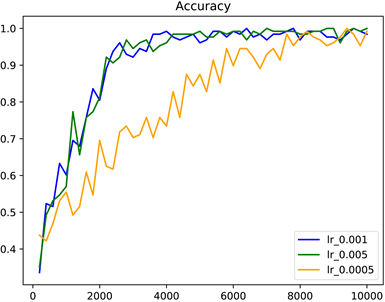
Figure 14. Performance of non-back propagation algorithms when using different learning rates

图14. 非反向传播算法在使用不同学习率时的表现

从图14可知，学习率为0.001与0.005时模型的收敛速度几乎相同，但当学习率设置为0.005时，模型的表现最优，当学习率为0.0005时，模型收敛速度明显较慢。学习率设置的越小可使模型的最终结果越接近最优解，学习率设置的越大则可使模型迭代的速度更快，因此，本文通过多组多次的实验，得到了权衡模型的收敛速度和模型的表现能力的学习率。

本文将基于非反向传播的人脸表情识别算法与Alexnet，Inception v2，Resnet 50进行了比较，学习率均为0.005，batch size均为128，在使用相同的环境及时的结果如图15所示。

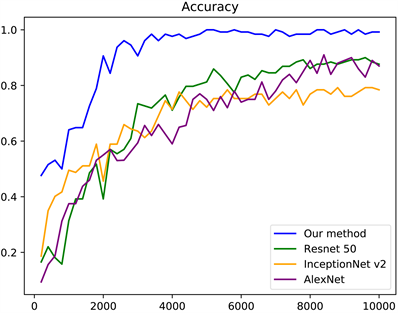
Figure 15. Accuracy curves of different models using the same environment and parameters

图15. 使用相同的环境及参数时不同模型的准确率变化曲线

从图15中可看出，本文提出的算法的收敛速度明显比其他算法快，与反向传播相比，HSIC-Bottleneck更好地分离了单个神经元表示中的隐藏信号，这表明HSIC-Bottleneck目标有助于使提取到的特征的分布更加独立，更容易与其标签相关联，且最终的准确率与其他反向传播算法的准确率相差不多。其中每种算法迭代一步的运行时间及在测试集上的最终结果如表1所示。

Table 1. Detection speed and average accuracy of different models on the test set

表1. 不同模型在测试集上的检测速度及平均准确率

从表1中可看出，本文提出的算法在达到与传统反向传播算法的准确率的同时大幅提高了运行速度，并且在模型收敛速度上更快、计算量更小、内存占用更小，证明了本文提出的算法性能更好，优化方法可行。

5. 结束语

本文提出了一种基于非反向传播稠密卷积神经网络的人脸表情识别算法，采用HSIC-Bottleneck代替传统的梯度反向传播，首先训练一个类似对输入变量编码的网络，从而更容易得到与输出相关的所需信息，使用HSIC-Bottleneck作为训练目标，在没有反向传播的情况下训练深度神经网络，然后用训练好的网络在深造训练期间为分类器提供更良好的特征，进一步改善网络算法的性能，使用Adam优化器，但没有反向传播。HSIC-Bottleneck训练网络，可以删掉输入信息中的冗余，并加强和标签数据的相关性，优化了隐藏层的输出信息，加快了模型的收敛速度，避免了反向传播中出现的梯度弥散、梯度爆炸问题，大幅减少了分类任务中的计算量。前馈网络采用基于attention机制的稠密卷积神经网络结构，更加充分地利用了提取到的特征，在对小物体保持敏感的同时也能很好的学习物体的整体特征。实验结果表明，较其它传统深度学习算法，非反向传播的稠密神经网络算法在人脸表情识别任务中的训练速度、准确率和计算量有巨大优势。

本文提出的非反向传播神经网络，属于端到端任务，能够自动提取输入数据的特征，不需要人工干预，在人脸表情识别方向取得了很好的效果，其检测结果远远高于一般机器学习的方法。但是端到端的学习任务往往需要大量的有标签数据，这对于缺少标签数据的表情识别领域提出了很大的挑战，同时也是下一步要研究的重点。

NOTES

^*通讯作者。