1. 研究背景
森林生态系统在全球碳循环中发挥着重要的作用 [1] ,其提供的生态系统服务功能具有不可替代的作用 [2] [3] 。土壤表面二氧化碳通量(土壤呼吸,Rs)约占森林生态系统呼吸总量的69%,是陆地生态系统第二大碳通量 [4] 。土壤呼吸(F)是陆地生态系统第二大碳通量 [5] ,温带森林土壤呼吸总量占生态系统呼吸总量的近70%,对于维持局域和全球碳平衡具有举足轻重的作用。准确量化土壤呼吸对于估算净生态系统CO2交换量(NEE)和校验涡动协方差技术测量结果不可获缺 [6] 。
不同的土壤呼吸速率(Rs)测算方式会对F的计算结果造成影响 [7] ,不同的计算方式所考虑的影响因素不同,所建模型也不同,各自对每周乃至全年生长季F的影响大小都不同,本次实验利用三种测算方式对F结果进行交互验证,帮助我们加深理解不同模型各自的优缺点,为F的准确评测提供科学依据。
本研究采用动态密闭箱–红外气体分析仪法,连续监测林龄为25年(平均树龄)的蒙古栎林生态系统土壤呼吸速率(每次测量的时间间隔为1周),样地阴、阳坡各3次重复,样方9次重复,共测量29次,同步测定土壤温湿度T5、W5,主要解决以下科学问题:1)建立蒙古栎林土壤呼吸速率(Rs)与土壤温湿度关系经验模型;2) 基于线性内插法理论,分析不同模型推算土壤呼吸速率(Rs)和通量(F)的差异。
2. 研究方法
2.1. 研究区域概况
研究样地位于吉林省东南部,通化市境内(E125˚59'20'', N41˚44'3'')。该区域位于长白山脉的西南部,属中温带湿润气候区,年平均气温5.5℃,一月份平均气温最低,常年平均在零下14℃左右,极端最低气温达−33℃;七月份平均气温最高,在22℃左右,极端最高气温36℃。通化地区多年平均降水量有870 mm,主要集中在夏季,6~8月三个月的降水量占年总降水量的60%以上,年日照时数高达2200小时。该区域地带性土壤为暗棕壤,植被为砍伐后形成的天然次生林,主要包括蒙古栎林、落叶松林及红松人工林。
研究区域为蒙古栎天然次生林,林龄25年(平均树龄,生长锥法测定)。蒙古栎的胸高断面积比例超过90%,伴生树种有紫椴(Tilia amurensis Rupr.)和色木槭(Acer mono Maxim.),乔木密度为1333株/hm2,胸高断面积22.30 m2/hm2,胸径14.34 ± 0.31 cm,树高8.21 ± 0.49 m。
2.2. 土壤呼吸速率的测定
分别在蒙古栎林阳坡(SU,西偏南21˚,坡度22˚)和阴坡(SH,东偏北21˚,坡度31˚)设置3块样地(20 m × 30 m),阴阳坡样地最小直线距离小于50 m。每个样地随机布置土壤环3个,环高5 cm,内径19.5 cm,土壤环一端处理成楔形以便压入土壤并减少对土壤的镇压作用。每个土壤环露出地面3 cm,在整个生长季测定过程中土壤环的位置固定。利用挖壕法在每个样地边缘随机设置异养呼吸(RH, µmol CO2 m−2·s−1)样方3个(1 m × 1 m),观测期间去除样方内所有活体植物。利用LGR便携式温室气体分析仪(915-0011, Los Gatos Research Inc., San Jose, USA)配备土壤呼吸气室(PS3000, Lica United, Beijing, China)观测土壤呼吸速率(RS, µmol CO2 m−2·s−1),通过差减法(RS-RH)计算根际呼吸(RR, µmol CO2 m−2·s−1)。通过该仪器自带温湿度探头就近同步测量土壤环周围5 cm深度土壤温度(T5, ℃)和土壤体积含水量(W5, RH%)。测量自2017年4月12日开始,10月28日结束,测量时间步长为一周,共观测29次。实验样地外500米左右设置自动气象站(CR1000, CSI Campbell, USA),用于自动观测空气和土壤温、湿度、太阳辐射和降水等环境因子。
2.3. 数据分析
对于单次观测结果而言,阳坡和阴坡土壤呼吸速率和土壤温湿度数据为同一天的观测结果(两个坡向观测间隔 < 3 h),假设以上3个指标在观测期间无明显的时间动态 [8] ,通过配对数据T-test检验两个坡向温度、水分和土壤呼吸速率的差异,利用Person相关系数描述两个坡向土壤温度、水分和土壤呼吸速率的变化趋势的一致性。
下面是Q10模型和Gammar模型的原始方程:
① Q10模型:
② Gammar模型:
蒙古栎林分布的土壤环境比较干旱、贫瘠,考虑到土壤温度与土壤湿度的交互作用可能对土壤呼吸速率产生一定的影响。上式中T为T5,W为土壤5 cm处土壤体积含水量W5 (RH%)或月降水量P (mm),a、b、c、d为方程系数。建模前进行对数转换以满足线性和方差齐性,建模时选择向后剔除法,先建立全模型再根据设定的判定依据剔除不符合判据的变量,直到回归方程中不再含有不符合判据的自变量为止。
通过每月观测的土壤呼吸瞬时速率的平均值(
, µmol CO2 m−2·s−1)和当月的天数(D)估算土壤呼吸当月的排放通量(F, g C m−2),生长季总通量为月通量的累加值,具体计算方式如下:
3. 研究结果
3.1. SPSS求得的阴阳坡各自的Q10和Gammar模型方程
我们以一年所观测得到的实验数据进行模型推算分析,最终得到蒙古栎林阳坡和阴坡的Rs与W、T之间的Q10和Gammar模型方程如下:
1) 阳坡:
① Q10:
② Gammar:
2) 阴坡:
① Q10:
② Gammar:
3.2. 三种模型推算的F分析
我们运用上述计算得到的两种模型以及线性内插法三种方法去推算阳坡(图1)、阴坡(图2)的F值。发现同一批数据,通过三种计算方式推导,最终得到的F值之间存在一定的差异。其中,阳坡用两模型求得的每周F值均呈单峰曲线形式,而用线性内插法求得的则是双峰曲线形式;阴坡三种方法求得的F均呈双峰曲线形式。两种模型所求得的每周阴阳坡F趋势相同,且Q10模型所求得的值都比Gammar模型求得的值大。无论是阴坡还是阳坡,前期三种模型求得的F趋势基本一致,中期差异较大,后期相对较吻合。此外,我们通过两模型所求得的F峰值均出现在第17周,而线性内插法求得的峰值则出现在第18周。
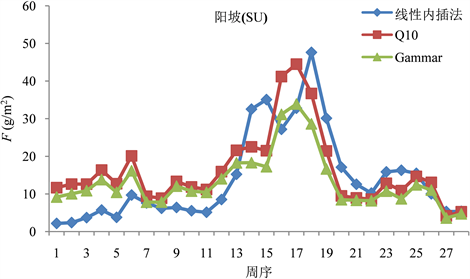
Figure 1. F value of sunny slope calculated by three models
图1. 三种模型推算的阳坡F值
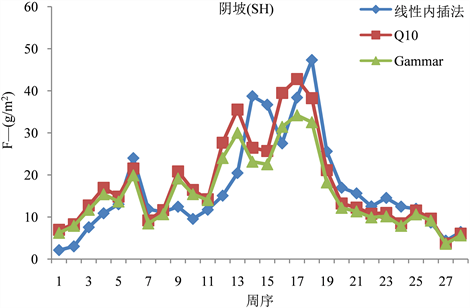
Figure 2. F value of shady slope calculated by three models
图2. 三种模型推算的阴坡F值
3.3. 两两方法之间的数据比较分析
对线性内插法和Gammar模型求得的F值进行比较,我们发现,当线性内插法求得的F值小于9.46 g/m2时,Gammar模型求得的F值为高估,反之为低估(图3)。
将线性内插法和Q10模型求得的F值进行比较,得到当线性内插法求得的F小于18.04 g/m2时,Q10模型求得的F值为高估,反之为低估(图4)。
分析Q10法和Gammar模型法求得的F值之间的关系,结果发现,两模型计算得到的F值拟合度很高,无论是阴坡还是阳坡数据,R2均达0.99,而当F逐渐增大时,两模型所求得的F值差异增加(图5)。
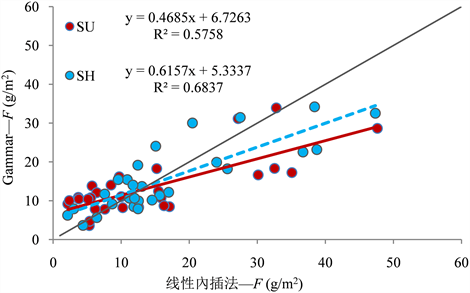
Figure 3. Comparison of F values obtained by linear interpolation method and Gammar model
图3. 线性内插法与Gammar模型求得的F值比较

Figure 4. Comparison of F values obtained by linear interpolation method and Q10 model
图4. 线性内插法与Q10模型求得的F值比较

Figure 5. Comparison of F values obtained by Gammar model method and Q10 model
图5. Gammar模型法与Q10模型求得的F值比较
3.4. 阴、阳坡每月土壤呼吸通量的比较
分析阳坡数据可以发现,在4月、6月、9月线性内插法与两模型求得F差异显著,但两模型各自之间差异不显著(图6)。对阴坡数据进行分析发现,仅9月三种方式求得的F值存在显著差异(图7)。另外,通过对阴、阳坡数据之间进行比较,发现通过三种方式求得的每月F,阳坡存在差异的月份明显较阴坡多,而在生长季中期求得的F值差异较生长季前后期小。
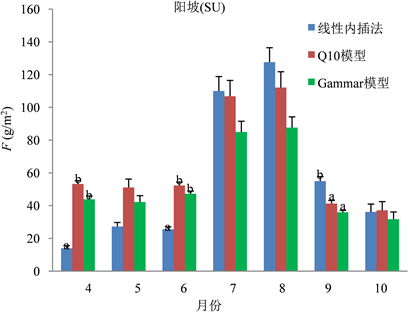
Figure 6. Comparison of F values obtained by three methods on sunny slope
图6. 阳坡三种方法求得的F值比较
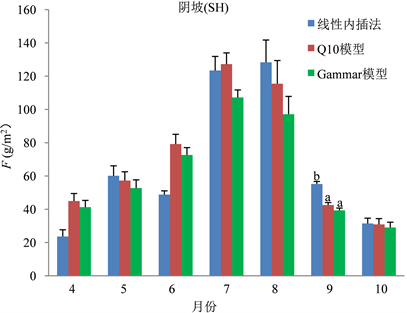
Figure 7. Comparison of F values obtained by three methods of shady slope
图7. 阴坡三种方法求得的F值比较
4. 研究结论
根据本研究的结果,我们发现蒙古栎林土壤呼吸速率(Rs)的主要影响环境因子为土壤温度和土壤湿度。无论最终计算运用哪个模型,在最终的回归方程中都会含有交互作用项。
首先,阴坡、阳坡两个坡向蒙古栎林土壤呼吸值对应的主要影响因子不同,这会导致最终拟合的模型自变量和系数也相应地出现不同。其次,在对用两模型计算的F值进行比较的过程中发现,Q10模型和Gammar模型的拟合精确度较高。结合模型模拟的F结果,生长季早期(4月、6月)和晚期(9月)的精度均低于生长季中期(7月、8月)。对比阴坡和阳坡的数据发现,用模型模拟得到的阴坡F值准确效果比阳坡好,出现这一差异的原因极有可能是阴坡土壤水分高于阳坡,即阴坡受土壤水分胁迫的程度较阳坡小导致的。综上,我们可以得出,Q10模型和Gammar模型拟合出的F值在生长季的中期都低估了,但Q10模型低估程度(5.74%)比Gammar模型低估程度(23.12%)更小,所以我们认为Q10模型比Gammar模型更适于描述本地区蒙古栎林Rs与土壤温湿度之间的关系。