基于改进遗传禁忌搜索混合算法的二维矩形件排样问题研究

Research on Two-Dimensional Rectangular Part Layout Problem Based on Improved Genetic Tabu Search Hybrid Algorithm

摘要: 矩形件排样问题在实际生产中占据着很大的份额。本文主要针对矩形件排样问题中的零件定序问题进行研究。并基于此提出了自适应遗传禁忌搜索算法的序列优化方法，以此来提高矩形件的板材利用率。此算法以遗传算法为全局搜索算法，并通过自适应确定选择、交叉、变异算子的方式对其进行了改进。同时，采用禁忌搜索算法对已经进入收敛稳定阶段的种群进行局部搜索。通过此种方法来找到排样最优序列。实验结果表明：遗传禁忌搜索混合算法在提高板材利用率方面具有很好的效果。

Abstract: The layout problem of rectangular parts occupies a large proportion in actual production. In this paper, the problem of part sequencing in rectangular part layout is studied. Based on this, a sequence optimization method of adaptive genetic tabu search algorithm is proposed to improve the utilization rate of rectangular plates. This algorithm takes genetic algorithm as the global search algorithm, and improves it by adaptively determining the selection, crossover and mutation operators. At the same time, the tabu search algorithm is used to locally search the population that has entered the stage of convergence and stability. This method is used to find the optimal nesting sequence. The experimental results show that the hybrid algorithm of genetic tabu search has a good effect in improving the utilization rate of plates.

1. 引言

二维矩形件的排样问题实际上就是一个组合优化问题，即将矩形零件以一个高效的策略在待切割板材上进行合理的布局 [1] 。一个合理的排样策略可以实现板材利用率的最大化，实现板材的高效利用。达到节省板材使用原料、节省生产成本。

矩形板材排样序列优化策略在二维矩形件的排样问题中起着至关重要的作用，直接影响了板材的利用率。目前对于板材排样问题的研究层出不穷。Leung S C H，Zhang D，Sim K M等人提出了将二维模板排样问题中的排序与局部搜索和模拟退火算法相结合的两段式思想，并以此来增强算法的搜索能力 [2] 。Charalambous与Fleszarb在满足面积平均性原则的情况下对矩形板材的方向和旋转进行限制，提出一次性构建排样策略 [3] 。Eunice Lopez-Camach等人利用主成分分析法降低了实例特征的维数，同时生成2D模型。但是此种方法在对一些面积较小的零件排样时并不能取得很好的效果 [4] 。Ayadiy与Masmoudi结合了粒子群优化算法与启发式算法。完成了对具有一定约束限制的矩形板材的切割。该方法相较于试验对比数据在板材利用率上提高了2.6% [5] 。郭蕴华等人在对排样定序时使用了蚁群算法并对其进行了改进，在定位方面使用了剩余矩形方法，以此来提高板材的利用率 [6] 。

本文针对矩形板材的排样序列优化问题进行研究，提出了自适应的遗传算法，并使用禁忌搜索算法对其进行改进，以此来对板材定序问题进行优化。实现了提高矩形板材的利用率。

2. 问题描述与数学模型

2.1. 矩形件排样问题描述

在不同的领域，矩形件排样问题根据需求的不同也会存在或多或少的差异。但总的来说可以概括为二维矩形件排样的基础性问题。总体上讲，矩形件排样问题就是：在一块已知宽度为W长度不限的矩形模板M上，将一定数量的长宽已知的矩形件集合 $P=\left\{p_1,p_2,p_3,\cdots ,p_n\right\}$ 紧密排布。同时在矩形零件排放过程中要满足以下三个要求：

1) $p_i$ 与 $p_j$ 不能够有重叠的部分； $i\ne j;i,j=1,2,3,\cdots ,n;$

2) $p_i$ 不能超出矩形模板的边界； $i=1,2,3,\cdots ,n$ ；

3) $p_i$ 的边界在矩形模板上的排放一定是与模板边界平行的。

2.2. 矩形件排样问题数学模型建立

我们可以通过建立的矩形板材的数学模型对矩形件排样问题进行详细的阐述。

矩形板材的数学模型为如下：

$Y=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_i{l}_i}}{W\ast L}$ (1)

$\forall p_i,p_j:p_i\cap p_j\ne \varnothing ;i,j=1,2,3,\cdots ,n$ (2)

$s.t.\{\begin{array}{l}\forall p_i;0\le x_i\le W,0\le x_i+w_i\le W;y_i\ge 0;\hfill \\ \forall p_i;0\le x_i+w_i\le W\wedge 0\le y_i+w_i\le W;\hfill \end{array}$ (3)

其中，Y：板材利用率； $w_i$ ：矩形零件宽度； $l_i$ ：矩形零件长度；L：零件在矩形模板上所占面积的最小长度；式(2)表示了零件不重叠，式(3)表示矩形零件板材没有超出矩形模板边界。

3. 遗传算法与禁忌搜索混合算法

遗传算法与禁忌搜索混合算法利用两种算法各自的优点进行互补，从而实现了在矩形件排样时的序列优化问题。利用禁忌搜索算法较强的局部搜索寻优的特点，避免了遗传算法陷入局部最优的情况。从而使矩形件排样能够得到更优的排样序列。

3.1. 遗传算法

3.1.1. 遗传算法介绍

遗传算法(Genetic algorithms, GA)是一种通过模拟自然进化的过程来搜索最优解的方法 [7] 。该算法通过模拟基因的交叉、变异过程，可以对组合优化问题快速获得比较优异的解。Holland基于自然界优胜劣汰的思想提出的串编码思想为遗传算法的发展奠定了良好的基础 [8] 。

3.1.2. 自适应遗传算法的方法设计

遗传算法的每一次优化都取决于前一次优化，在此过程中，通过突变操作引入新的“基因”，进而对过程产生重大变化。然而，通常使用的逐渐降低的突变率使得算法无法立即对突然的变化做出反应。本文提出了一种自适应的遗传算法(Self-adaption genetic algorithms, SAG)。

具体流程如下图1所示。

1) 基因编码

在遗传算法的编码方式选择上，目前有很多形式，本文中选取的是路径编码的方式。即直接以板材的序号进行组合形成的一串编号。例如：零件的顺序为{1, 2, 3, 4, 5, 6}，零件的编码方式就可以表示为{6, 5, 2, 3, 1, 4}，这就表示矩形件的排样序列为6 > 5 > 2 > 3 > 1 > 4。

2) 适应度函数的建立

适应度函数(Fitness function, FF)又称为评价函数。对于任何进化算法，需要FF根据解决问题的适合性来对中种群中的每个个体来进行评估。种群中的个体基于适应度的值来决定是否适应环境，此参数为“优胜劣汰”最为基础和重要的一环。

本文采用以矩形件排样中模板的利用率为基准，判断在固定高度下，模板材料的使用情况。采用2.2节中的公式(1)为适应度函数。

$f\left(x\right)=Y=\frac{{\displaystyle \underset{i=1}{\overset{n}{\sum }}{w}_i{l}_i}}{W\ast L}$ (4)

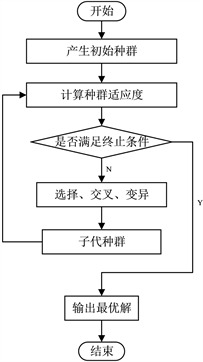
Figure 1. Flow chart of genetic algorithm

图1. 遗传算法流程图

3) 选择算子的确定

一个种群中的两个个体经过交叉和变异来产生新一代的子个体，这就是种群的繁衍。但是，并不是在种群中的任意两个个体之间都能进行繁衍的。只有满足一定条件的两个个体之间才能进行繁衍子代的过程，而这个特定的条件就是父代的选择操作。

本文使用轮盘赌选择方法来选取父代个体：

$p\left(x\right)=\frac{f\left(x_i\right)}{{\displaystyle \underset{j=1}{\overset{n}{\sum }}f\left(x_j\right)}}$ (5)

其中 $p\left(x\right)$ 为种群中个体遗传概率。

4) 交叉算子选择

在基因编码模块提到，采用路径编码的方式在基因进行交叉是可能会出现基因重复的现象。所以需要对基因的交叉、重组操作进行特殊的处理。为此，研究人员提出了一些重新排列的操作。主要有：部分匹配交叉(Patrially Matched Crossover, PMX)、顺序交叉(Ordered Crossover, OX)、循环交叉(Cycle Crossover, CX) [9] 。

本文采取顺序交叉(Ordered Crossover, OX)来进行基因交叉排列操作。例如：选中的父代1的编码为(5, 2, 3, 7, 6, 1, 4)，选中的父代2的编码为(4, 6, 2, 1, 3, 5, 7)，则顺序交叉过程如下图2所示。

如图2所示，当父代1中的交叉位置为 $d_1=3$ 、 $d_2=5$ 时，将父代1中 $d_1$ 至 $d_2$ 之间的基因保留到子代1中相同的序列上。同时，子代1中的其它位置基因依照父代2中除去与父代1中重复的基因的其它基因顺序填充。子代2的生成原理与此相同，不再进行阐述。

其中交叉算子采取自适应交叉概率，公式如(6)所示：

$p_{\mathrm{cov}}=\{\begin{array}{l}\frac{f_{\max }-\max \left(f\left(y_1\right),f\left(y_2\right)\right)}{f_{\max }-f_{avg}},\max \left(f\left(y_1\right),f\left(y_2\right)\right)>f_{avg}\hfill \\ {\omega }_1,\max \left(f\left(y_1\right),f\left(y_2\right)\right)<f_{avg}\hfill \end{array}$ (6)

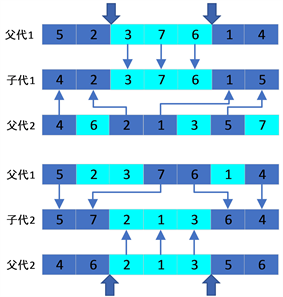
Figure 2. Cross generation of offspring from individual genes of two parents

图2. 两父代个体基因交叉生成子代

其中， $f_{\max }$ 是种群中适应度最大的个体， $\max \left(f\left(y_1\right),f\left(y_2\right)\right)$ 表示进行两个父代中适应度较高的那个个体， $f_{avg}$ 表示平均适应度， ${\omega }_1$ = 0.6。

5) 基因变异操作

本文变异采取的是随机选择两个序号的交换位置进行交换来实现的。如：一个父代个体满足了变异条件，随机产生变异的位置为p₁，p₂。父代个体Y的基因编码为Y = (6, 3, 1, 4, 5, 2, 7)；p₁ = 2，p₂ = 6；则产生变异之后的基因序列为：Y’ = (6, 2, 1, 4, 5, 3, 7)，变异过程如下图3所示。

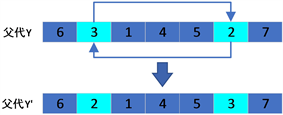
Figure 3. Variation process diagram of offspring individuals

图3. 子代个体发生变异过程图

变异算子的确定采用自适应的方式，如公式(7)所示：

$p_{mut}=\{\begin{array}{l}\frac{f_{\max }-f\left(x\right)}{f_{\max }-f_{avg}};f\left(x\right)>f_{avg}\hfill \\ {\omega }_2;f\left(x\right)\le f_{avg}\hfill \end{array}$ (7)

其中， $f_{\max }$ 是种群中适应度最大的个体， $f\left(x\right)$ 表示即将进行变异父代的适应度， $f_{avg}$ 表示平均适应度， ${\omega }_1$ = 0.5。

3.2. 禁忌搜索算法

3.2.1. 禁忌搜索算法介绍

Gover教授提出一种基于单解的元启发式算法–禁忌搜索算法(Tabu Search, TS)，该算法在启发式局部搜索过程中可以逃避局部最优 [10] [11] 。因此，本文使用禁忌搜索算法对可能进入早熟期的遗传算法进行改进，跳出局部最优解。禁忌搜索算法的独到之处在于它能够利用特有的记忆功能引导局部搜索跳出局部最优，从而转换为全局最优解。

3.2.2. 禁忌搜索算法的关键参数

1) 初始解和候选解

本文初始解就选取3.1节所提过的矩形件的序列号。即遗传算法进入早熟期的种群中的各个子个体。候选解集是由邻域中的邻居组成，是一个比较关键的参数。可以选取邻域解集中的最优邻居，同时也可以在领域解集中随机选取。

设适配函数为 $P\left(X\right)$ ，则：

$P\left(X\right)=Y=\frac{{\displaystyle \underset{i=0}{\overset{n}{\sum }}{w}_i{l}_i}}{W\times L};$ (8)

2) 适配值函数

候选解集是由邻域解集中的优良集组成的，而这些优良解是通过适配函数筛选出来的。适配函数一般是由目标函数直接构成的。在本文中，我们选取板材的利用率来充当适配函数。以矩形模板的利用率来选取优良解集。

3) 禁忌表

禁忌表是一种存储结构，它可以存放在运行过程中被禁忌的对象。设置禁忌表就可以有效避免搜索时出现重复搜索的情况。其中被禁忌的对象就称为禁忌对象，禁忌对象通常为找到的局部最优解。而禁忌对象不能被选使用的最大次数就是禁忌长度。当禁忌对象的允许迭代次数为0时，该对象就会被解禁。

4) 特赦规则

特赦规则就是在算法的迭代时设置一种特殊的规则，通过此种规则来判断被禁的对象是否可以在禁忌补偿不为0的情况下依然可以被选中。本文中采用适配值来设置特赦规则，也就是当 $P\left(x_{now}\right)>P\left(x_{best}\right)$ 时，候选解 $x_{now}$ 优于当前最优 $x_{best}$ 。此时满足被解禁的条件，就可以忽略禁忌步长，直接选中候选解为最优解。

3.2.3. 禁忌搜索算法的流程

禁忌搜索算法的流程可以简单概括为：

Step 1：选定一个初始解 $x_1$ ；禁忌表 $H=\varnothing$ 。

Step 2：如果满足终止准则，则输出结果。否则进行下一步。

Step 3：在 $x_i$ 的邻域 $N\left(x_i\right)$ 中选择候选解 $Can\_N\left(x_i\right)$ ；在 $Can\_N\left(x_i\right)$ 中选择一个评价最优的解 $x_{i+1}$ 。若 $x_{i+1}$ 不在禁忌表中，选为当前解，否则从不在禁忌表中的解中选择一个最优解。

Step 3：重复step 2，知道满足停止条件。

具体流程如下图4所示：

3.3. 遗传–禁忌搜索混合算法

经研究表明，GA拥有较好的全局搜索能力，但是容易陷入局部最优，进入早熟期。而TS具有很好的局部搜索能力。因此，考虑两者的优点结合起来提出遗传禁忌搜索混合算法。当遗传算法经过一定的迭代后，使用TS对种群中的每一个个体进行局部搜索来增加种群的多样性。遗传算法与禁忌搜索算法比较如下表1所示：

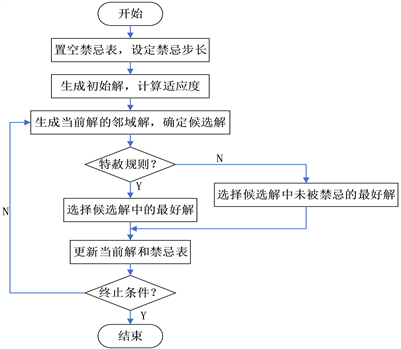
Figure 4. Tabu search algorithm flowchart

图4. 禁忌搜索流程图

Table 1. Comparison between tabu algorithm and genetic algorithm

表1. 禁忌算法与遗传算法比较

下面给出遗传禁忌搜索算法的计算步骤：

Step 1：编码，随机产生一定数量的初始种群。

Step 2：计算个体的适应度。

Step 3：种群进行选择、交叉、变异操作。

Step 4：判断种群是否进入早熟期，若进入早熟期，转到Step 5；否则转到Step 2。

Step 5：在陷入局部最优的群体中随机选曲个体 $P_i$ 作为当前初始解 $x_1$ ；设最优解 $x_{best}=x_1$ ；设置禁忌表H为空。

Step 6：确定邻域解 $N\left(x_i\right)$ 与候选解集合 $Can\_N\left(x_i\right)$ 。

Step 7：在 $Can\_N\left(x_i\right)$ 中选择一个评价最优的解 $x_{i+1}$ 。若 $x_{i+1}$ 不在禁忌表中，选为当前解，否则从不在禁忌表中的解中选择一个最优解。

Step 8：判断是否满足终止条件；如果满足，则输出 $x_{best}$ ；否则，将当前对象放入到禁忌表中，转到Step 5。

遗传–禁忌搜索混合算法流程图5如下：

4. 实验结果分析

与传统的遗传算法相比较，本文所提出的改进算法在一定程度上提高了矩形件排样序列的优化结果，使矩形板材的利用率得到一定的提高。为了验证遗传–禁忌搜索混合算法在矩形件排样问题中的实用性与可行性，本文以传统的遗传算法为类比对象，通过实验数据对比来验证本文算法的优越性。

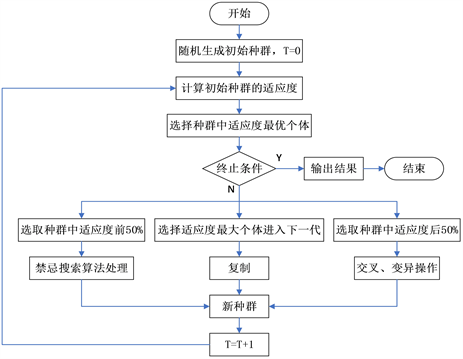
Figure 5. Flow chart of genetic tabu search hybrid algorithm

图5. 遗传禁忌搜索混合算法流程图

本文两种算法采用相同的种群数量和迭代次数，详细参数如下表2所示：

Table 2. Algorithm parameter table

表2. 算法参数表

本文选取两组数据进行验证对比试验，第一组实验采用数量较少的矩形件进行对比，具体信息如下表3、表4所示：

Table 3. Rectangular template information table

表3. 矩形模板信息表

Table 4. Rectangular part information table

表4. 矩形零件信息表

待排放零件的尺寸信息与数量如下表5所示：

Table 5. Dimension information table of rectangular parts to be discharged

表5. 待排放矩形件尺寸信息表

其中基于改进的遗传禁忌搜索算法排样优化结果如图6所示：

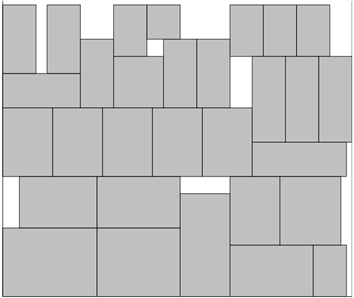
Figure 6. Optimal nesting results based on genetic Tabu search hybrid algorithm

图6. 基于遗传禁忌搜索混合算法的最优排样结果

第二组实验数据则采用数量比较多的矩形件进行排样分析，具体信息如下表6、表7所示：

Table 6. Rectangular template information table

表6. 矩形模板信息表

Table 7. Rectangular part information table

表7. 矩形零件信息表

待排放零件的尺寸信息与数量如下表8所示：

Table 8. Dimension information table of rectangular parts to be discharged

表8. 待排放矩形件尺寸信息表

其中基于改进的遗传禁忌搜索算法排样优化结果如图7所示：

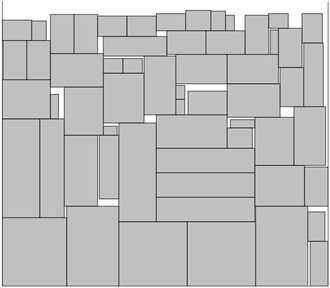
Figure 7. Optimal nesting results based on genetic Tabu search hybrid algorithm

图7. 遗传禁忌搜索混合算法最优排样结果

为避免偶然性时间发生，实验中对每个测试用例均进行10次实验，与传统的遗传算法优化结果相对比，详细对比结果如下表9所示：

Table 9. Experimental results of algorithm

表9. 算法实验结果

由表9数据可以看出，对比于传统的遗传算法优化结果，自适应遗传禁忌搜索算法在板材利用率上第一组上升了1.02%，第二组数据的板材利用率上升了2.76%。因此采用本文算法可以有效提高板材的利用率。

5. 结论

本文针对矩形件排样问题建立了数学模型。并以此提出了自适应的遗传禁忌搜索算法来优化板材排样序列。经试验验证，此算法具有很好的序列优化能力。并能得出结论：

1) 所采用的自适应的遗传禁忌搜索算法可以有效地提高板材的利用率。

2) 与传统的遗传算法对比，本文算法更加适用于矩形板材排样序列的优化。

3) 本文算法可以有效解决传统遗传算法的陷入局部最优解的缺点，提高种群的多样性。