1. 引言
2022年11月,文化和旅游部发布的《关于推动在线旅游市场高质量发展的意见(征求意见稿)》(以下简称《意见》)。其中提到“积极发挥在线旅游行业在旅游业中的枢纽和引领作用,推动旅游行业的创新发展和智慧化水平”,“提升行业管理的数字化水平和治理能力,推动中国在线旅游行业发展处于国际领先地位”,这无疑给在线旅游行业注入了新的活力。
在线旅游,指消费者通过网络的方式购买和预订旅游产品或者旅游服务,并通过互联网或者线下完成支付。最早在1999年,中国便产生了在线旅游行业,但是在当时互联网普及较低,发展受到了阻碍。后来随着技术的进步,在经过长达20年的发展与更迭后,在线旅游与国民经济的关系越来越密切了,形成了相互依赖、相互促进的关系。
因此研究和预测该行业股票走势,能帮助我们了解在线旅游行业的发展趋势,可以给广大投资者提供投资决策参考,本文选用在线旅游板块中龙头股之一的西域旅游股票作为研究对象。西域旅游开发股份有限公司是新疆地区第一家旅游开发行业的上市公司,以2022年11月2日的股价估算市值超40亿元。
2. 文献综述
目前,国内外对于股票价格的预测有很多研究,但是股票市场复杂多变,且交易往往具备一定随机性。由于受到市场内外部宏观环境、投资者微观因素等诸多不确定的影响,无疑增大了预测的难度,因此在研究方法上一直不断进行改进、优化和创新,并致力于形成更加稳定有效的预测体系。
针对股票价格的预测,国内外学者提出了方差分析、回归分析、模糊算法、遗传算法、马尔可夫链等预测模型。其中马尔可夫链的作为深度学习的基石,且应用比较广泛。例如,张宇山等人 [1] 将股价状态划分成六个区间,利用马尔可夫链构建转移概率矩阵,预测宝钢股份未来20个交易日的走势;彭志行等人 [2] 将23个精伦电子股票收盘价分成四个区间,通过构建转移概率矩阵预测未来两个交易日的收盘价。王佳伟等人 [3] 则利用神经网络和马尔可夫链结合的方式,预测特发信息股票的价格。
基于以上文献,本文通过马尔可夫模型来研究西域旅游(300859)的股价涨跌变化情况,探究马尔可夫链在预测股票价格中的实际应用。我们收集整理了西域旅游股票2022年7月29日至2022年11月2日的收盘价格,按照涨幅共划分成四个区间,构建四状态转移概率矩阵和十六状态转移概率矩阵,预测股票未来的走势情况。
3. 马尔可夫链模型介绍
马尔可夫链,是以俄国数学家安德烈·马尔可夫(A.A. Markov, 1856~1922)命名的,是随机过程领域中的重要研究方法之一。如果n个连续变动事物在变动过程中,其中任一次变动的结果都具有无后效性,那么,这n个连续变动事物的集合就叫做马尔可夫链,表明事物的状态由过去到现在、由现在到将来,一环接一环,像一根链条 [4] 。
马尔可夫预测法是基于马尔可夫链,是依据当前事件的情况来预测其在未来各个时期变化情况的一种预测方法。总结历史数据,形成状态转移概率矩阵,对预测对象各个状态的初始分布和各状态间的转移概率进行研究,在已知当前股价涨跌情况时,便可以预测下一时刻股票的涨跌情况。
3.1. 马尔可夫模型分析法
用马尔可夫链模型对事件进行预测的方法被称为马尔可夫模型分析法,这是一种将研究的变量作为状态,变化过程作为“状态转移”,形成动态模型来研究随机事件变化趋势的方法。
股票市场的股票价格、收盘价格、涨幅情况都是一种依赖于时间t的随机变化的过程,并且股票未来的状态只与当下时刻状态有关,与过去无关。股票状态变化的过程是具有时间历程的不变性的,并且其一步转移概率与时间起点没有关系,只与时间差有关系,即转移概率矩阵稳定不变。同时股票价格、股票价格区间以及成交量只能产生可列个状态,且用同一标准划分的各状态应相互独立,并包含全部可能出现的状况 [5] 。所以,可以用马尔可夫模型分析法对股票市场的价格波动、未来发展趋势进行预测,探究马尔可夫链在预测股票价格中的实际应用,帮助投资者了解市场基本情况。
假设马尔可夫过程
的参数集是T离散的时间集合,即
。与
对应的全体可能取值组成了状态空间I,即
。
马尔可夫链 [6] 则是指,在随机过程
中,对于任意整数
,其条件概率满足马尔可夫链的后无效性,即:
(1)
换言之,时刻
的状态条件概率仅仅依赖于时刻
的状态,与其他时刻的状态无关。
3.2. 转移概率与转移概率矩阵
状态转移概率是指事物当前正处于某一状态,其下一时刻转移到其他状态的可能性。我们可以借助条件概率的定义,求解转移概率p。例如事物从状态
到状态
的状态转移概率
为:
(2)
如果事物拥有n个可能的状态,即
。那么,我们把
记为事物从状态
转移到
状态的转移概率,若事物此刻正处于状态
,其下一刻可能会转移到
的状态,共n种可能。总结所有的状态转移概率后,可得到矩阵P:
(3)
如果矩阵P满足下列条件:
式(4)要求矩阵P满足非负性,即矩阵中所有元素均不得为负,且均不大于1。
式(5)要求矩阵P满足归一性,即矩阵所有行和始终为1。
若矩阵P满足以上两点,我们称为P为状态转移概率矩阵。
3.3. 马尔可夫预测法
事物如果要转移到某种特定状态时,在实际过程中可能需要进行多步才能达到。本文用
表示事件在初始状态(
)已知的情况下,经过k次状态转移后,到达状态
的概率。其具备以下性质:
(6)
我们可以把上述过程分解成两步:事物先经过
次的状态转移至
的状态,再经过1次状态转移成
的状态。根据马尔可夫过程的特性两步之间相互独立,由Bayes条件概率公式其概率表示为:
(7)
如果我们考虑经过k次状态转移后,所有可能转移到状态的概率,我们用行向量
来表示:
(8)
当k = 0时,我们称为初始态概率向量
(9)
结合式(7),我们可以推导出只用初始状态向量和状态转移矩阵,表达
的方法:
(10)
4. 在线旅游板块股票案例分析
选用在线旅游板块中的西域旅游(300859)股票作为本文研究对象,收集该股自2022年7月29日至2022年11月2日的交易数据(详细数据见附表1),股票价格折线图如图1所示:
我们将西域旅游从2022年7月29日至2022年11月2日期间的每日收盘价与上一个交易日收盘价格进行比较,把涨幅在
区间内的定义为大幅下降,把涨幅在
的股票定义为大幅上涨,位于
和
分别定义为上涨、下降。即总共分为大幅下降、下降、上涨、大幅上涨这四种情况,将这四种情况分别作为马氏链模型中的四种状态,利用马尔可夫链进行分析预测。
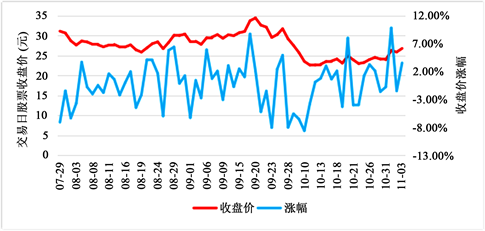
Figure 1. Stock price line chart of western region tourism from July 29, 2022 to November 2, 2022
图1. 西域旅游2022年7月29日~2022年11月2日股价折线图

Table 1. Daily closing price status of western region tourism from July 29, 2022 to November 2, 2022
表1. 西域旅游2022年7月29日~2022年11月2日每日收盘价状态
4.1. 划分状态确定状态空间
以每个收盘日作为离散的时间单位,收盘价变动情况分为四种状态:大幅下降、下降、上涨、大幅上涨。并把大幅下降记为0(DD)、下降记为1(ND)、上涨记为2(NR)、大幅上涨记为3(DR)。则状态空间为
。
状态概率是各种状态出现的可能性大小,用状态向量
,其中
,T是时间集,
,
为状态i出现的概率(
)。
表1中共63个交易日,其中大幅下降10、下降22、上涨25、大幅上涨6。
4.2. 建立状态转移概率矩阵
设
为
从状态u经过一步转移到状态v的频数,我们可以通过式(11)用来估计
。
(11)
在表1中,大幅下降状态的总次数为10次,其中由大幅下降转移为大幅下降的次数是3,故转移概率为:
;由大幅下降转移为下降的次数是4,故转移概率为:
;由大幅下降转移为上涨的次数是2,故转移概率为:
;由大幅下降转移为大幅上涨的次数是1,故转移概率为:
;
下降状态的总次数为22次,其中由下降转移为大幅下降的次数是2,故转移概率为:
;由下降转移为下降的次数是7,故转移概率为:
;由下降转移为上涨的次数是10,故转移概率为:
;由下降转移为大幅上涨的次数是3,故转移概率为:
;
上涨状态的总次数为25次,其中由上涨转移为大幅下降的次数是4,故转移概率为:
;由上涨转移为下降的次数是8,故转移概率为:
;由上涨转移为上涨的次数是12,故转移概率为:
;由上涨转移为大幅上涨的次数是1,故转移概率为:
;
大幅上涨状态的总次数为6次,其中由大幅上涨转移为大幅下降的次数是0,故转移概率为:
;由大幅上涨转移为下降的次数是3,故转移概率为:
;由大幅上涨转移为上涨的次数是2,故转移概率为:
;由大幅上涨转移为大幅上涨的次数是1,故转移概率为:
,将其各状态转移概率列成表2。

Table 2. Table of state transition probability
表2. 状态转移概率表
表2中的所有元素组成了矩阵P,且满足非负性和归一性,因此P为所求的状态转移概率矩阵:
4.3. 计算各收盘日状态概率
本文将不同时期的状态概率向量用
表示,根据式(10)计算不同时期的向量。由表1可知,由于第64日收盘价处于下降状态,而无后继资料 [7] ,所以可以认为初始状态向量
,利用该向量和状态转移概率矩阵来预测以后各个收盘日价格状态概率。
第64日收盘价状态概率向量:
第65日收盘价状态概率向量:
第66日收盘价状态概率向量:
第67日收盘价状态概率向量:
第68日收盘价状态概率向量:
将以上结果变化为列表3:

Table 3. The predicted probability of each closing day
表3. 各收盘日状态转移预测概率
4.4. 构造十六状态概率转移矩阵
从表3中计算值可以看出,该股的收盘价状态的变化趋势:随着交易日的增加,即n足够大时,只要状态转移概率矩阵不变(即稳定条件),则状态概率会趋向和初始状态无关的值,并稳定下来,适合长期预测。即该股票在长期有42%左右的可能性处于上涨状态,35%的可能性处于下降状态,14%的可能性处于大幅下降状态,10%的可能性处于大幅上涨状态。预测的结果与实际情况基本一致。因此,该股的前景还算不错。
马尔可夫链系统长期预测条件:
其中P为概率转移矩阵:
我们将概率转移矩阵P代入式中,即:
(其中,
)。
求得:
可以看出,由稳定状态下计算出的收盘价格状态概率值与递推公式推导的结论一致。我们利用数据来计算股票的期权价值,并分析人们对于股票涨势的看法。
设昨日、今日连续两天大幅下降称为状态1a (DDDD),昨日下降、今日大幅下降称为状态2a (NDDD),昨日上涨、今日大幅下降称为状态3a (NRDD),昨日大幅上涨、今日大幅下降称为状态4a (DRDD);
设昨日大幅下降、今日下降称为状态1b (DDND),设昨日下降、今日下降称为状态2b (NRND),设昨日上涨、今日下降称为状态3b (NRND),设昨日大幅上涨、今日下降称为状态4b (DRND);
设昨日大幅下降、今日上涨称为状态1c (DDNR),设昨日下降、今日上涨称为状态2c (NDNR),设昨日上涨、今日上涨称为状态3c (NRNR),设昨日大幅上涨、今日上涨称为状态4c (DRNR);
设昨日大幅下降、今日大幅上涨称为状态1d (DDDR),设昨日下降、今日大幅上涨称为状态2d (NDDR),设昨日上涨、今日大幅上涨称为状态3d (NRDR),设昨日大幅上涨、今日大幅上涨称为状态4d (DRDR)。
据表1,股票价格模型可看作十六状态的马尔可夫链。例如:
以此类推,其转移概率矩阵P如下:
其中,第四行的概率总和为0,因为在表1中不存在昨日大幅上涨、今日大幅下降的情况。
4.5. 多阶十六状态概率转移矩阵
二阶转移概率矩阵
为:
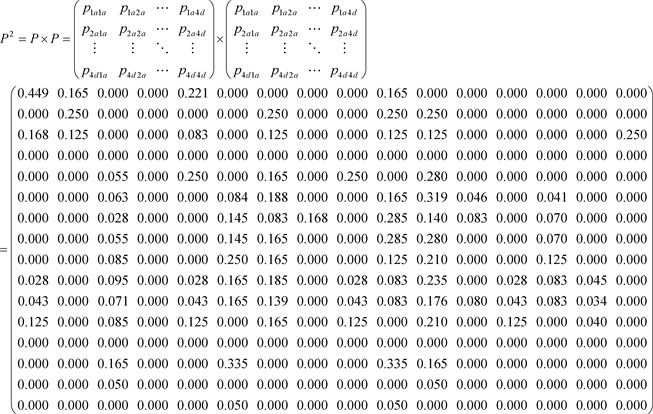
昨日、今日股票价格大幅下降,后天股票价格大幅下降的概率
;
昨日、今日股票价格大幅上涨,后天股票价格下降的概率
;
昨日、今日股票价格上涨,后天股票价格上涨的概率
;
昨日、今日股票价格下降,后天股票价格下降的概率
。
这样,我们以两天的股票状况对股票未来进行预测,增加了预测系统的稳定程度,在金融方面具有一定的实际意义。
转移概率矩阵
为:

5. 预测与检验
我们利用概率矩阵预测第64日(11月3日)的股票情况,已知第62、63日收盘价分别处于大幅上涨、下降的状态,从十六状态转移矩阵P来看,第64日处于下降和上涨的状态各0.5,没有明显的倾向;我们从第64日收盘价状态概率向量
来看,收盘价转移到上涨状态的概率最大,达到0.45;因此预测第64日股票收盘价涨幅在
区间范围内;实际第64日收盘价涨幅为3.37%,位于区间范围内,预测结果准确;
预测第65日(11月4日)的股票情况,从十六状态转移矩阵
和从第65日收盘价状态概率向量
来看,第65日位于上涨状态的概率最大,即预测收盘价涨幅在
区间内;实际第65日收盘价涨幅为12.57%,不位于区间范围内,但预测和实际都在上涨;
预测第66日(11月7日)的股票情况,第66日收盘价状态概率向量
中下降状态的概率较前一天有所增加,再结合十六状态转移矩阵
进行分析,第66日位于下降状态的概率会较大一些,即预测涨幅在
区间内;实际第66日收盘价涨幅为−1.40%,位于区间范围内,预测准确,这也体现了随着状态的增多系统的稳定程度在增加。
6. 结论
本文利用马尔可夫模型对西域旅游股票少量的历史数据对股票收盘价格进行预测和分析,结果表明预测与实际结果比较相符。但是仍有预测结果与实际股票波动不吻合的状况,归根结底在于股票还受到市场环境、经济政策、汇率变化、政治等因素的影响。根据东方财富网的资料显示,2022年11月4日创业板指数上涨幅度超过3%,本文认为11月4日涨幅不在预测区间内的主要原因:模型没有考虑到创业板股票当天市场交易环境因素的影响,使得预测涨幅略微保守。
因此,我们要综合考虑各种因素,并随着股票收盘价的更新,及时调整状态转移概率矩阵,从而提高预测结果的可信度,也为投资者提供参考依据,为公司股价提供参考走势。
基金项目
本论文工作由北京市属高校基本科研业务费(No. 110052971921/103)和北京市教委基本科研业务费(No. KM202010009013),大学生科学研究与创业项目(X202210009106)资助。
附录

Table A1. Stock data of western region tourism from July 29, 2022 to November 3, 2022
表A1. 西域旅游2022年7月29日~2022年11月3日股价数据
NOTES
*通讯作者。