基于改进人工势场法的无人车路径规划算法研究

Research on Path Planning Algorithm of Unmanned Vehicle Based on Improved Artificial Potential Field Method

摘要: 针对传统人工势场法路径规划中存在的局部极小值和目标不可达等问题，本文提出了一种人工势场法的改进方法。首先，定义障碍物的碰撞范围并建立基于角度的影响范围，排除无人车前方一定距离和角度内的任何障碍物，从而将它们的影响降到最低。其次，为了解决目标不可达问题，通过新增目标点与无人车的距离因子改进斥力函数。最后，针对局部极小值问题，在障碍物碰撞范围外创造虚拟目标点。利用Matlab对所提出的改进算法进行验证，仿真结果表明了规划算法的避障有效性、安全性以及可跟踪性。

Abstract: To address issues such as local minima and unreachable targets that arise in path planning using the traditional artificial potential field method, an enhanced approach to the artificial potential field method has been proposed in this paper. First, define the collision range of obstacles and establish an angle-based influence range to exclude any obstacles within a certain distance and angle in front of the unmanned vehicle, thereby minimizing their impact. Secondly, in order to solve the problem of unreachable targets, the repulsion function is improved by adding the distance factor between the target point and the unmanned vehicle. Finally, for the local minimum problem, a virtual target point is created outside the obstacle collision range. The proposed improved algorithm is verified by Matlab, and the simulation results show the effectiveness, safety and traceability of the planning algorithm for obstacle avoidance.

1. 引言

近年来，无人驾驶车辆广泛应用于民用和军事领域，承担了智能运输、紧急救援以及军事行动等重要任务 [1] [2] [3] 。路径规划作为无人驾驶车辆领域关键技术之一，是无人驾驶车辆运动控制的基础，路径规划的有效性直接影响无人驾驶车辆平稳安全行驶的能力，也是环境信息感知系统和车辆智能控制的桥梁 [4] 。局部路径规划能够实时获取障碍物信息并进行实时规划，使无人车有更好的环境适应性，因此局部路径规划已成为国内外研究的热点。目前，常见的局部路径规划算法有遗传算法、模糊逻辑算法、神经网络算法、人工势场法等。人工势场法具有出色的实时避障能力，可以从周围环境采集车辆与障碍物的信息，规划出可行路径。这种方法不需要对全局环境进行搜索，具有实时性强、运行效率高、计算量小且规划路径平滑等诸多优点。因此，它适用于安全性和实时性要求较高的无人车驾驶车辆路径规划 [5] [6] [7] 。

人工势场法是一种广泛用于无人驾驶车辆路径规划的方法，但是存在目标不可达和局部最小值的缺点 [8] [9] 。近几年，研究人员针对传统人工势场法存在的缺陷提出了各种改进措施。Rostami等 [10] 在传统人工势场函数中加入调节因子来绕过障碍物从而克服局部最小值和目标不可达问题；赵明等 [11] 提出自适应域–人工势场法，通过动态调节势场值来解决局部极小值问题，但是当障碍物影响范围较大时，这种方法会极大地增加所生成的运动路径；陈冠星等 [12] 通过新增虚拟目标点引导车辆走出陷阱区域，虽解决了部分局部极小值的情况，但是未解决目标不可达问题；Yao等 [13] 从强化学习的视角来解决复杂环境问题，将黑洞人工势场和强化学习结合来解决局部极小值的问题，但在路径规划过程中会出现振荡现象；王迪等 [14] 提出基于虚拟目标点和环境判断的改进方法，实现无人车的局部路径规划，但在遇到陷入U型障碍物时规划出“沿壁走”的路径，此时规划出的路径并不是最优路径；马庆禄等 [15] 改进引力场函数的距离阈值和调节因子，解决了目标不可达的问题，但是没能解决局部极小值的问题。

针对传统人工势场法在路径规划中存在的不足，本文提出了以下解决方案：首先，定义障碍物的碰撞范围，排除无人车前方一定距离和角度内的任何障碍物，从而将障碍物对无人车的影响降到最低；其次，为了解决目标不可达问题，通过新增目标点与无人车的距离因子进行改进斥力函数；最后，针对局部极小值问题，在障碍物碰撞范围外作切线构造虚拟目标点。最终生成一条能够有效躲避障碍物且顺利到达目标点的最优路径。

2. 传统人工势场法

人工势场法是由Khatib于1986年首次引入到移动机器人路径规划算法中的，其本质上是将移动机器人的工作环境视为一个抽象的虚拟力场。在这个虚拟力场中，机器人在引力和斥力的合作用下，朝着目标点不断移动 [16] 。

无人驾驶车辆在二维坐标系中的位置坐标为 $q{\left(x,y\right)}^T$ ，目标点的坐标为 $q_{goal}{\left(x_{goal},y_{goal}\right)}^T$ 。车辆会一直受到目标点的引力势场的作用，引力势场大小与当前位置到目标点的距离成正比。则引力势场函数 $U_{att}$ 的表达式为：

$U_{att}=\frac{1}{2}\eta {\rho }^2\left(q,q_{goal}\right)$ (1)

公式(1)中： $\eta$ 为引力势场正比例系数； $\rho \left(q,q_{goal}\right)$ 为车辆当前位置与目标点之间的距离一个矢量，方向从车辆指向目标点。无人驾驶车辆所受到的引力为引力势场的负梯度，对引力势场函数求导可得到引力函数 $F_{att}$ ，其表达式为：

$F_{att}=-\nabla U_{att}=-\eta \rho \left(q,q_{goal}\right)\frac{\partial \rho \left(q,q_{goal}\right)}{\partial x}$ (2)

斥力势场取决于当前位置与障碍物之间的距离，当车辆在障碍物影响范围之外时，其所受到的斥力势场为零；车辆进入到障碍物影响范围之内时，随着两者之间距离的减小，车辆所收到的斥力势场会增大。障碍物的坐标位置为 $q_{obs}{\left(x_{obs},y_{obs}\right)}^T$ ，其所产生的斥力势场函数 $U_{rep}$ 的表达式为：

$U_{req,i}\left(q\right)=\{\begin{array}{l}\frac{1}{2}k{\left[\frac{1}{{\rho }_i\left(q,q_{obs}\right)}-\frac{1}{{\rho }_o}\right]}^2,{\rho }_i\left(q,q_o\right)\le {\rho }_o\\ 0,{\rho }_i\left(q,q_o\right)>{\rho }_o\end{array}$ (3)

公式(3)中： $\eta$ 为斥力势场正比例系数； ${\rho }_o$ 为斥力场作用范围， ${\rho }_i\left(q,q_{obs}\right)$ 为车辆当前位置与障碍物之间的欧式距离。无人驾驶车辆所受到的斥力为斥力势场的负梯度，对斥力势场函数求导可得到斥力函数 $F_{req,i}\left(q\right)$ ，其表达式为：

$F_{req,i}\left(q\right)=-\nabla U_{req,i}\left(q\right)=\{\begin{array}{l}k\left[\frac{1}{{\rho }_i\left(q,q_{obs}\right)}-\frac{1}{{\rho }_o}\right]\frac{1}{{\rho }_i^2\left(q,q_{obs}\right)}\frac{\partial {\rho }_i\left(q,q_{obs}\right)}{\partial x},{\rho }_i\left(q,q_{obs}\right)\le {\rho }_o\\ 0,{\rho }_i\left(q,q_{obs}\right)>{\rho }_o\end{array}$ (4)

在引力场和斥力场的基础上，得到总势场函数：

$U_q=U_{att}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{U}_{req,i}\left(q\right)}$ (5)

因此，无人驾驶车辆所受到的合力为：

$F\left(q\right)=-\nabla U\left(q\right)=F_{att}+{\displaystyle \underset{i=1}{\overset{n}{\sum }}{F}_{req,i}\left(q\right)}$ (6)

无人驾驶车辆存在引力与斥力的合力决定自动驾驶车辆的移动方向，随着合力的变化最终得到一条抵达目标点的路径 [17] 。当车辆在某一点所受到的合力为零或者合力方向与引力和斥力共线时，此时就会陷入局部极小值的情况，车辆将无法确定下一步的前进方向，可能会出现停止或者徘徊的情况。如果距离目标点很近有障碍物，由公式(4)可知，障碍物所产生的斥力随着距离的减小而增大。同时，由公式(2)可以计算出目标点所产生的引力，随着无人驾驶车辆行驶到目标点距离的减小，该引力逐渐变得很小，这就会使得无人驾驶车辆受到的势场合力一直指向目标方向的反方向，从而使得车辆停滞而无法到达预定目标点。这就是人工势场法存在目标不可达的问题。

3. 改进的人工势场法

3.1. 引入障碍物的影响范围

传统的人工势场法进行路径规划时，通过以无人驾驶车辆为圆心，以距离 $d_0$ 为半径创建一个圆，以此圆为影响范围来判断障碍物是否对无人驾驶车辆产生斥力，只要在此范围内的障碍物都要计算斥力。该方法在进行路径规划时，即使直线前进方向无障碍物，如果直线路径外且在受到影响范围内有障碍物干扰，无人驾驶车辆也可能无法生成最优路径，同时，当障碍物位于无人驾驶车辆运动方向反方向时，这些障碍物对运动是没有太大影响的，此时计算合力时也会受到这些障碍物影响。为了解决这个问题，引入了碰撞距离 $d_s$ 以及限制障碍物影响范围的角度 $\theta$ ，在特定范围内过滤掉障碍物干扰，该范围由无人驾驶车辆和障碍物的大小决定。如图1所示，在考虑无人驾驶车辆行驶方向的障碍物时，只考虑以无人驾驶车辆到目标点的运动方向角 $\phi$ 为中线，左右偏移角度为 $\theta$ 所形成的扇形区域内障碍物形成的斥力，其他角度的则不需要进行考虑 [18] ，同时，设 $r_i$ 为各个障碍物到无人驾驶车辆与目标点连线的直线距离，其中，以障碍物为圆心，碰撞距离 $d_s$ 为半径的圆为障碍物的碰撞影响范围，当 $r_i<d_s$ ，表示该障碍物存

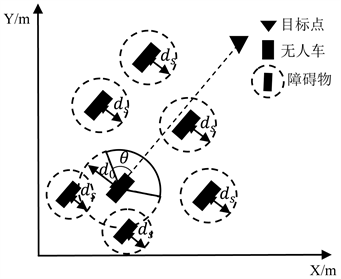
Figure 1. Collision range between unmanned vehicles and obstacles

图1. 无人驾驶车辆与障碍物存在碰撞范围

在碰撞风险，此时计算合力时需考虑该障碍物的斥力。反之，忽略该障碍物的斥力。

3.2. 改进斥力函数

在传统人工势场法进行路径规划时，当无人驾驶车辆到达目标点附近遇到障碍物时，障碍物所产生的斥力远大于目标点的引力，这就会导致车辆在目标点附件徘徊而无法到达目标点。针对该目标不可达的问题，需要对斥力势场函数进行改进，具体方法是在该函数中引入无人驾驶车辆与目标点的距离因数。

改进后斥力势场函数如下：

$U_{req,i}\left(q\right)=\{\begin{array}{l}\frac{1}{2}k{\left[\frac{1}{{\rho }_i\left(q,q_{obs}\right)}-\frac{1}{{\rho }_o}\right]}^2{\rho }^m\left(q,q_{goal}\right),{\rho }_i\left(q,q_{obs}\right)\le {\rho }_o\\ 0,{\rho }_i(q,q_{obs})>{\rho }_o\end{array}$ (7)

公式(7)中：m为大于零的任意常数；其余参数含义同公式(1)、(3)。m为距离因子调节系数， $\rho \left(q,q_{goal}\right)$ 为无人驾驶车辆距离目标位置的距离。

改进后的斥力仍为斥力场的负梯度，但是斥力是由两个不同方向上的分力组成，改进后斥力函数公式为(8)：

$F_{req,i}\left(q\right)=-\nabla U_{req,i}\left(q\right)=\{\begin{array}{l}{F}_{req1}+F_{req2},{\rho }_i\left(q,q_{obs}\right)\le {\rho }_o\\ 0,{\rho }_i\left(q,q_{obs}\right)>{\rho }_o\end{array}$ (8)

式(8)中： $F_{req1}$ 为斥力分量，方向由障碍物指向无人驾驶车辆，大小为：

$F_{req1}=k\left[\frac{1}{{\rho }_i\left(q,q_{obs}\right)}-\frac{1}{{\rho }_o}\right]\frac{1}{{\rho }_i^2\left(q,q_{obs}\right)}\cdot \frac{\partial {\rho }_i\left(q,q_{obs}\right)}{\partial x}{\rho }^m\left(q,q_{goal}\right)$ (9)

式(9)中： $F_{req2}$ 为引力分量，方向是无人驾驶车辆车指向目标点，大小为：

$F_{req2}=-\frac{m}{2}k{\left[\frac{1}{{\rho }_i\left(q,q_{obs}\right)}-\frac{1}{{\rho }_o}\right]}^2{\rho }^{m-1}\left(q,q_{goal}\right)\frac{\partial \rho \left(q,q_{goal}\right)}{\partial x}$ (10)

将 ${\rho }^m\left(q,q_{goal}\right)$ 增加到斥力函数中，起调节的作用，最终无人驾驶车辆的受力情况如图2所示。为了使无人驾驶车辆受到斥力的影响降低，需要保证斥力分量小于引力分量，同时需要保证无人驾驶车辆到达目标点时，引力分量达到最大，斥力分量为0，因此调节系数m取值需要大于0且小于1。通过对斥力的生成机制的改进，解决了目标不可达问题，进一步提高了无人驾驶车辆生成路径的成功率。

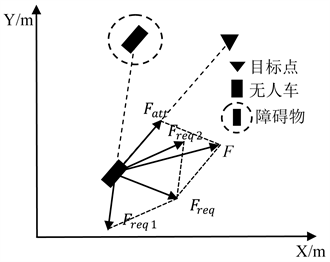
Figure 2. The force situation of the improved unmanned vehicle

图2. 改进后无人驾驶车辆的受力情况

3.3. 局部极小值优化

当障碍物处于无人驾驶车辆的斥力判断范围内，为了避免局部极小值，引入虚拟目标点来协助无人驾驶车辆避开障碍物。

在设置虚拟目标点时，该点离障碍物太远会导致规划的路径过长，导致计算量增加；该点离障碍物太近则会增加无人驾驶车辆的避障难度。为了解决此问题，本文通过在障碍物的碰撞范围外切点创造虚拟目标点，具体方法如下：

当有单个障碍物处于斥力判断范围内时，以该障碍物为圆心，碰撞距离 $d_s$ 为半径形成的圆，以无人驾驶车辆向此圆做两个切点为两个备用虚拟目标点，此时，如图3所示，两个切点所形成两个夹角分别为 ${\delta }_1$ 与 ${\delta }_2$ ，判断两夹角与无人驾驶车辆运动方向角 $\phi$ 之差的绝对值，较小的夹角对应的点为虚拟目标点。

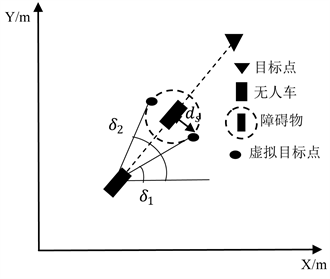
Figure 3. Virtual target point of a single obstacle

图3. 单个障碍物的虚拟目标点

当有多个障碍物处于斥力判断范围内时，以U型障碍物为例，选择相对于无人驾驶车辆运动方向角较小的最外侧障碍物的影响范围进行作切线，该切点为虚拟目标点。如图4所示。

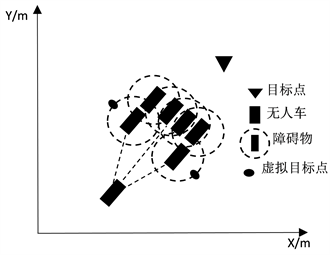
Figure 4. Virtual target points of multiple obstacles

图4. 多个障碍物的虚拟目标点

得到的虚拟目标点将临时代替最终目标点引导无人驾驶车辆前进，直到无人驾驶车辆到达虚拟目标点后，该虚拟目标点将消失，无人驾驶车辆的目标点变为最终目标点。

3.4. 算法步骤

本文提出的改进人工势场法算法流程如图5所示。

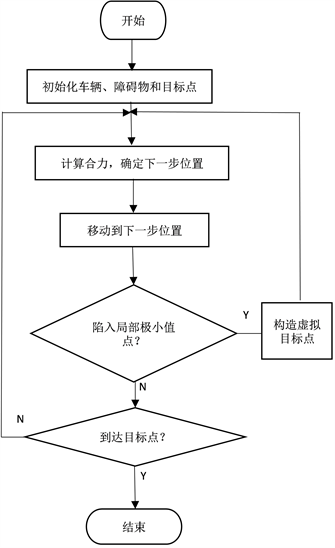
Figure 5. Improved algorithm design process

图5. 改进算法设计流程

4. 算法仿真与结果分析

本文创建基本环境和复杂环境进行仿真研究，以验证改进算法的可行性，改进算法将无人驾驶车辆视为一个质点。

为验证本文改进算法在解决局部最小值和目标不可达问题上的有效性，分别进行了两组对比仿真实验，本文算法和传统人工势场法在复杂环境下进行实验。

仿真基本参数如表1所示 [19] 。

Table 1. Simulation parameter setting

表1. 仿真参数设定

仿真结果与分析

图6(a)是传统人工势场法在常规障碍物环境中的仿真结果，如图可知：前半所规划的路线，在靠近障碍物的部分，可以看到离障碍物非常近，并且在目标点附近的障碍物前徘徊后无法前进，无法生成完整路径。

图6(b)为文献 [19] 的算法在常规障碍物仿真环境中的仿真结果。文献 [19] 中仅针对斥力函数进行改进，并没有加入障碍物影响范围。通过仿真结果可知，无人驾驶车辆虽然可以顺利到达目标点，但在路径规划的前期依然存在离障碍物较近，有碰撞风险。

图6(c)为本文在常规障碍物环境下对改进后人工势场法进行仿真后产生的结果。结果表明：改进后的路径相对平滑，在前期产生的路径，离障碍物较远，基本上都是靠着障碍物影响范围的边缘，这时几乎没有碰撞风险，同时规划的路线也可以顺利到达目标点。

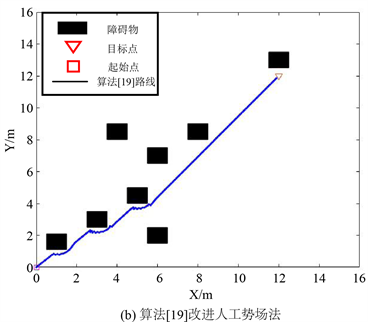
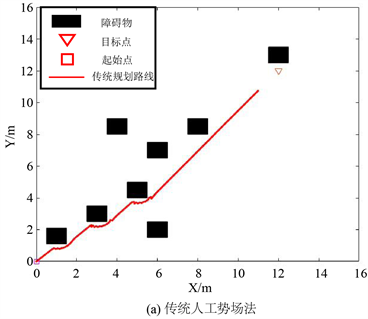
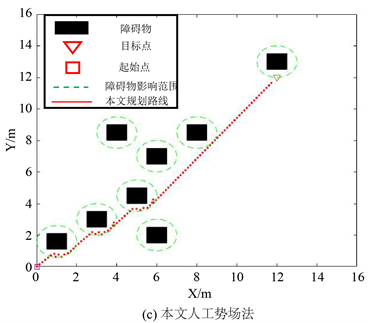
Figure 6. Comparison of unreachable targets

图6. 目标不可达对比

通过对仿真生成的实验数据进行对比，传统人工势场法所生成的路径并不能抵达目标点；利用文献 [19] 中的算法规划的路径虽然可以顺利达到目标点，但是规划的路径并不是特别平滑，使得其路径迭代次数较多，运行时间较长；如表2中所示，相对比而言，本文算法规划出的路径相对平滑且运行时间比文献 [19] 改进方法减少了25%。

Table 2. Simulation experiment data

表2. 仿真实验数据

针对人工势场法存在的局部极小值点问题，在复杂的U型障碍物环境下分别以传统人工势场法和本文改进后人工势场法进行仿真实验。

图7(a)为无人驾驶车辆在U型障碍物环境下以传统人工势场法作为路径规划算法进行仿真的结果。从图中可知，因斥力的作用车辆一直在U型障碍物内徘徊，陷入局部极小值，无法跳出，最终无法规划出完整路径。

图7(b)为无人驾驶车辆在U型障碍物环境下以本文改进后人工势场算法作为路径规划算法进行仿真的结果。从图中可知，车辆在遇到U型障碍物时，车辆在陷入局部极小值的地点增加了额外的虚拟目标点的指引力，使得车辆顺利跳出局部极小值点并进入下一运动状态，最终抵达目标点。

通过对图7(a)和图7(b)的对比，本文提出的虚拟目标点对传统人工势场法规划路径产生的局部极小值点问题有非常明显的改进，最终可以抵达目标点。

Figure 7. Comparison of local minima

图7. 局部极小值对比

5. 结论

针对传统人工势场法的局限性，本文提出通过改进斥力函数，在障碍物碰撞范围外构造虚拟目标点解决上述问题，并将改进后的算法与传统算法进行对比。结果表明，改进算法能够规划出一条可行的路径，无人驾驶车辆能够安全避开障碍物，顺利到达目标点。